基于改进PSO-SVM的噪声稳健建筑物变形监测方法

张建奇

(广州市城市规划勘测设计研究院, 广东 广州 510000)

0 引言

近年来随着社会经济发展水平的不断提升,各种高层,超高层建筑物如雨后春笋般涌现,这些高层建筑在长期的运行和使用过程中,受到冰雹降雨等恶劣天气、地壳运动以及人为不正确使用等因素的影响都会出现细微的结构形变,这些形变经过长时间积累达到一定程度时会带来安全隐患,严重时甚至会影响人民群众的生命财产安全[1-2]。因此实时、高精度的建筑物变形监测对安全事故的提前预警具有重要意义。全球定位系统(Global Positioning System, GPS)作为3S核心技术之一具备成本低廉,自动化程度高,全天时,全天候和高精度等优势,近年来被广泛应用于建筑物的变形监测中,基于GPS的建筑物形变监测也成了当前的研究热点[3-4]。

目前常用的建筑物形变监测方法是以多项式拟合为代表的数值计算法,该类方法的基本思想是基于已经观测到的形变数据去拟合出一条符合数据分布规律的多项式曲线,然后利用该多项式曲线对未来的形变趋势进行预测,已有试验表明,该类方法对于建筑物未来较短时间内的形变预测精度较高,而随着时间的推移,该类方法的预测精度会出现明显下降[5];以小波变换为代表的时频变换类方法采用小波基等函数将变形数据转化到特定的变换域,从变换域中寻找出形变数据的内在规律和发展趋势,从而实现对建筑物未来形变的有效预测,该类方法相对于数值计算法增加了信息提取的维度,能够获得更优的预测精度,但是由于建筑物变形数据具备典型的随机性和微弱性,不同小波基函数的选择以及分解层数的确定对预测结果会产生较大的影响,通常采用的经验试错法存在主观性强,运算量大的问题,影响了该类方法的推广应用[6-7];近年来随着人工智能技术的兴起与发展,将神经网络,支持向量机等新方法与传统变形监测数据处理相结合而产生的人工智能法逐渐引起了广大学者的注意,该类方法作为一种数据驱动方法,不依赖于精度的数学模型,并且在小样本条件下依然能够获得较高的预测精度[8-10]。

当前的研究大都认为GPS获取的监测数据全部为有用信息,而在实际工程实践中GPS监测数据中不可避免的会混杂着噪声等随机误差[11],建筑物的变形过程作为一种典型的随机性和微弱性过程,随机误差的存在会影响对数据中形变信息的提取,因此实际工程应用中要求变形监测方法在低信噪比条件下依然可以获得较高的预测精度。

针对上述问题,本文首先提出一种自适应变步长惯性因子迭代法对传统PSO(粒子群优化算法, Particle Swarm Optimization)算法进行优化,提升PSO算法的全局搜索能力和收敛速度,然后利用改进PSO算法对SVM(支持向量机, Support Vector Machine)拟合模型参数进行全局寻优,提升其变形监测精度和噪声稳健性。基于实测数据开展试验对所提方法进行验证,结果表明所提改进PSO-SVM方法相对于传统交叉验证SVM方法和小波方法能够获得更高的拟合性能,在低信噪比条件下优势能加明显,更适合于实际工程使用场景。

1 SVM拟合原理

SVM最早由Vapnik和Cortes于1995年提出,其理论基础是统计学习中的VC维和结构风险最小化,能够在有限的样本信息条件下实现模型复杂度和学习能力之间最优折中,由于其在小样本,非线性和高维模式识别中表现出了许多特有的优势[12-14],一经提出便被推广应用到函数拟合,数据分类识别等多个领域。

(1)

(2)

利用Lagrange乘子法对式(2)进行求解可以得到最终的SVM线性回归模型为:

(3)

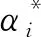
从式(3)可以看出,SVM回归模型的输出与(xi·x)有关,即只与xi和x的内积相关,因此与SVM分类模型类似,可以通过引入满足Mercer条件的核函数R(xi,x)实现由线性回归向非线性回归的转变,SVM非线性回归模型如下式(4)所示:

f(x)=w×φ(x)+b=

(4)

目前使用最多的核函数是式(5)所示高斯核,σ和u为核参数。

(5)

2 改进PSO-SVM算法原理

当核函数确定后,SVM拟合模型的性能受核参数σ和u的影响较大[17],目前常用的交叉验证法虽然在一定程度上提升了SVM模型的性能,但是当训练样本较少时会出现训练不充分,性能下降的问题,当训练样本充足时又存在运算量大,运算复杂的问题。因此需要一种自动寻优方法对SVM模型进行优化。

粒子群算法组作为一种经典的随机搜索算法,模拟的是自然界中鸟群的觅食行为,由于其算法简单,容易实现,具有较强的全局搜索能力且对随机误差不敏感等特点被广泛应用于模型优化领域。PSO实现全局寻优的基本准则是每个粒子在迭代过程中始终都在跟踪寻找到的粒子的最佳位置和当前种群中的最佳位置,从而不断对自身的速度信息和位置信息进行更新,从而使种群的运动由初始的无序发散状态逐渐向有序的收敛状态转变,并最终找到全局中的最佳位置。在这过程中,每个粒子的运动规律可以表示[15-16]:

(6)

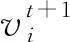
(7)

其中,t为当前迭代次数;T为总迭代次数。wmax为w能够取到的最大值,从式(7)可以看出,开始迭代时,t较小,此时w接近最大迭代步长,随着迭代次数的增加,t逐渐逼近于总迭代次数T,w随之减小。

根据上述分析,所提改进PSO-SVM算法步骤可以总结为以下六步:

步骤1:根据描述的问题确定训练样本集;

步骤2:PSO初始化,将SVM需要优化的核参数作为PSO算法的初始粒子,并设置粒子的起始位置信息和速度信息,根据式(7)设置惯性因子和终止条件;

步骤3:根据所要描述的问题选择合适的SVM核函数;

步骤4:计算当前状态下每个粒子的适应度函数,即计算当前状态下的pg和pi;其中,pg表示整个种群的位置,pi表示第i个粒子的位置。

步骤5:更新粒子的速度和位置信息,计算更新后粒子的适应度函数,将其与上一步骤的适应度函数值进行对比,令更优适应度函数值对应的粒子状态为当前状态;

步骤6:判断是否满足步骤二中设置的迭代终止条件,若满足,则迭代终止,此时的粒子即为最优SVM模型参数;否则转向步骤四继续迭代。

3 实例分析

3.1 数据介绍

导致建筑物出现形变的因素有很多,例如气候因素,人为使用因素,地壳运动因素等等,因此建筑物的形变通常会呈现出随机性,微弱性,不确定性和离散性等特征。文献[18]在对不同变形监测数据随时间变化曲线的分析基础上提出可以将建筑物形变过程分为三种类型:减速-匀速型,匀速-增速型和复杂变化型,其中前两种变化较为平稳,呈现出一定的规律性,相对而言预测容易,精度较高,而后者会出现一定的位移突变,导致预测性能往往较差。本文以匀速-增速型和复杂变化型建筑物形变数据为例开展试验。

图1和图2分别给出了某高层建筑(30层高商场)楼顶L024号监测点连续20期位移数据和某高塔(47.3 m高)塔顶L1号监测点连续30期位移数据变化曲线,可以看出高层建筑变形曲线服从上述匀速-加速型,而高塔由于年代较为久远,变形曲线为复杂变化型。

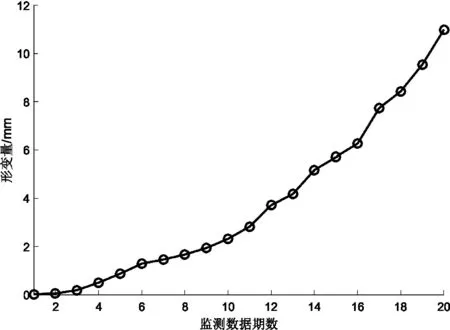
图1 高层建筑20期形变数据曲线

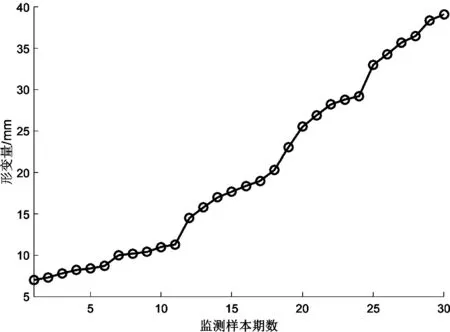
图2 高塔30期形变数据曲线

试验过程中,将两组试验数据的前一半数据作为训练样本,用于模型训练。剩余一半数据作为测试样本,验证模型的预测性能。SVM核函数选为经典高斯核,采用所提PSO算法对核参数进行全局寻优,PSO算法的加速因子c1=c2=2,种群规模设置为30,最大迭代次数设置为200,采用如下的最小均方误差作为适应度函数:

(8)

3.2 试验结果及分析

表1和表2分别给出了利用所提改进PSO-SVM(简称PSO-SVM)算法对高层建筑和高塔的形变数据预测结果,同时给出了采用传统小波方法(db4母小波,5层分解)和SVM方法(交叉验证确定核参数)在相同条件下开展试验获得的预测结果作为对比,其中对于表1的高程建筑数据, PSO-SVM模型中SVM核参数为经过全局寻优后获得的核参数为σ=0.7,C=25.8,而传统交叉验证获得的SVM核参数为σ=1.3,C=22.1,对于表2的高塔数据, PSO-SVM模型中SVM核参数为经过全局寻优后获得的核参数为σ=0.36,C=7.4,而传统交叉验证获得的SVM核参数为σ=0.85,C=9.9。

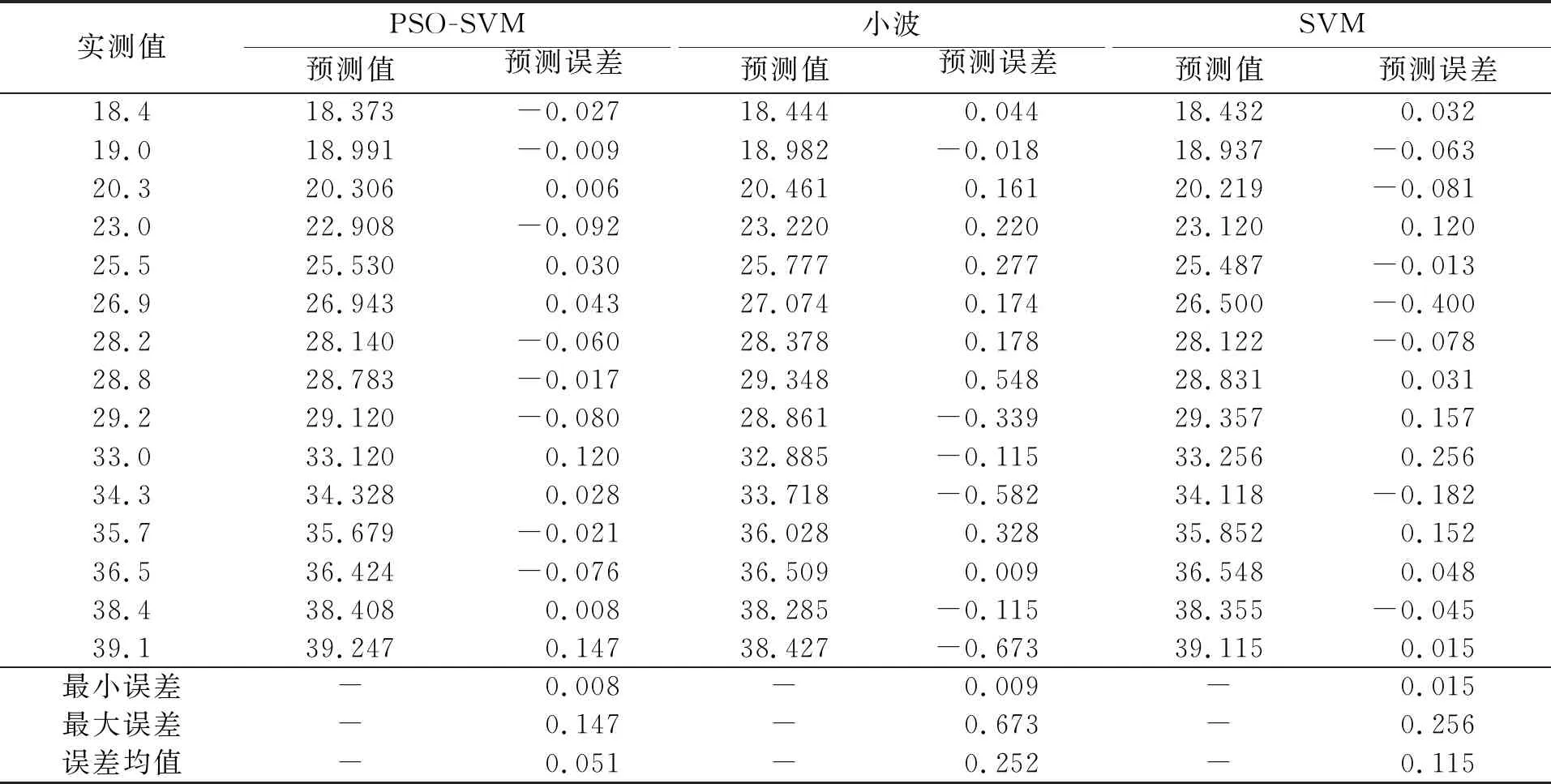
表2 高塔预测结果 单位：mm

从表1可以看出,由于高层建筑变形数据呈现出匀速-增速型的规律性变化趋势,三种方法都能够获得较好的预测精度,其中小波方法获得的最小预测误差为0.004,最大预测误差为0.085,误差均值为0.061。传统SVM获得的最小预测误差为0.002,最大预测误差为0.071,误差均值为0.042。PSO-SVM模型能够获得的最小预测误差为0.001,最大预测误差为0.020,误差均值为0.006。可以看出在最小误差,最大误差和误差均值三个方面,PSO-SVM方法均获得了最优的预测性能。从表2给出的结果可以看出,由于高塔的变形数据的规律性较差,三种方法的预测性能都呈现出了不同程度的下降,其中小波方法获得的最小预测误差为0.009,最大预测误差为0.673,误差均值为0.252,误差均值相对于表1的结果恶化了0.191;传统SVM获得的最小预测误差为0.015,最大预测误差为0.256,误差均值为0.115,误差均值相对于表1的结果恶化了0.073。PSO-SVM模型能够获得的最小预测误差为0.008,最大预测误差为0.147,误差均值为0.051,相对于表1的结果恶化了0.045。从上述结果可以看出,对于变化较为复杂的高塔数据,PSO-SVM在最小误差,最大误差和误差均值三个方面均获得了最优的预测性能。同时对比表1和表2的预测结果可以看出,对于变化趋势不同的数据,PSO-SVM方法表现出了更强的数据适应性,更加适合实际工程应用场景。

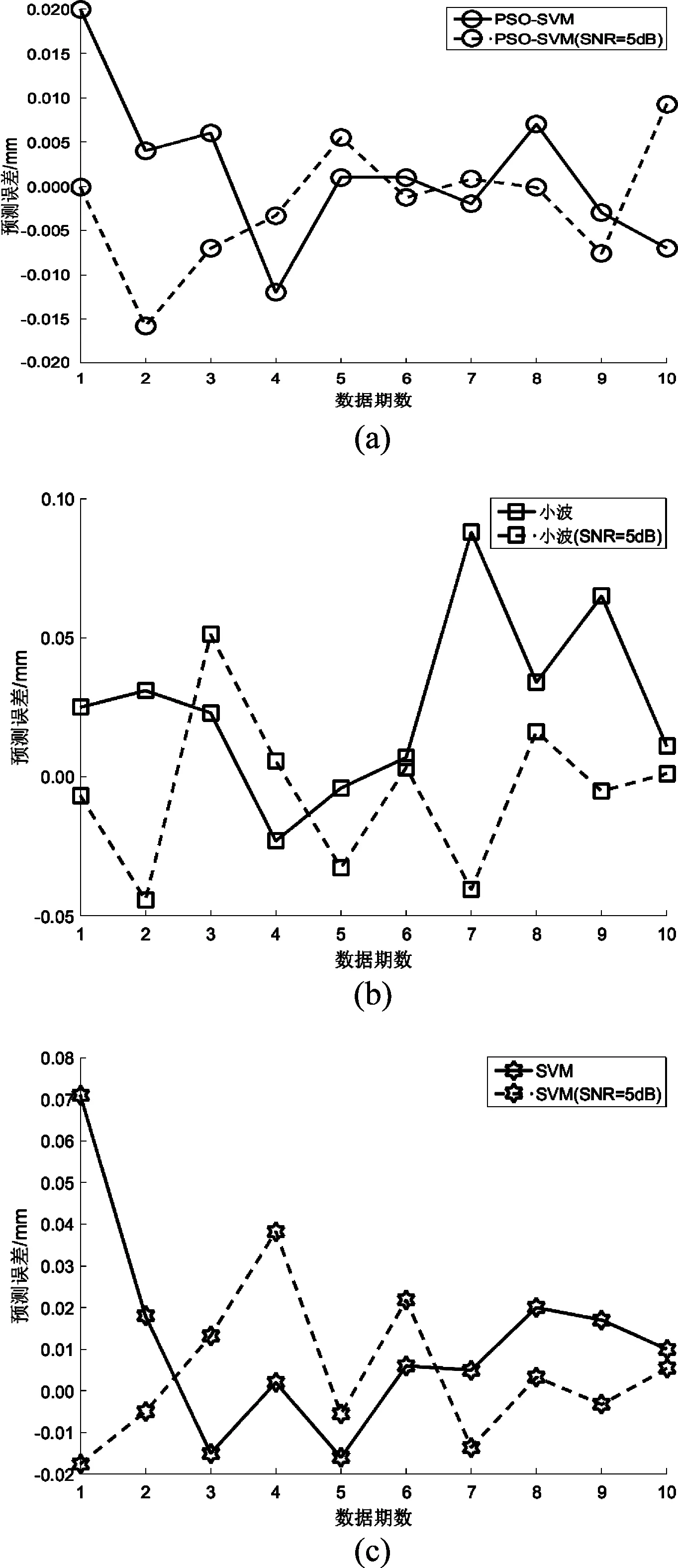
图3 不同方法对高层建筑预测结果

为了进一步验证不同方法在低信噪比条件下的预测性能,采用MATLAB自带的AWGN()函数向图1和图2所示变形监测数据中加入高斯白噪声,使数据的信噪比(Signal to Noise Ratio, SNR)降低到5 dB,在这种条件下利用PSO-SVM方法,小波方法和交叉验证SVM方法进行预测。为了直观的对比不同方法在低信噪比条件下的预测性能,图3给出了对高层建筑形变数据利用PSO-SVM方法,小波方法和交叉验证SVM方法获得的预测结果与真实值之间的误差。其中图3(a)中圆圈实线和圆圈虚线分别为PSO-SVM方法对应表1中的预测结果和SNR为5 dB情况下的预测结果;图3(b)中方框实线和方框虚线分别为小波方法表1中的预测结果和SNR为5 dB情况下的预测结果;图3(c)中五角星实线和五角星虚线分别为SVM方法表1中的预测结果和SNR为5 dB情况下的预测结果。同样图4给出了三种方法对高塔形变数据的预测结果。

从图3和图4给出的结果可以看出,信噪比降低后小波方法和传统SVM方法的预测精度都出现了较为明显的下降,而PSO-SVM方法几乎没有受到信噪比的影响,这是由于PSO算法的参数搜索空间为整个参数空间,噪声的存在对单个点会影响较大,但是对于整个参数空间可以认为噪声的谱密度是非常低的,同时PSO算法采用的是多粒子集群搜索方式,相对于单个粒子具有更强的噪声鲁棒性。

图4 不同方法对高塔预测结果

4 结束语

本文提出一种基于改进PSO优化SVM的噪声稳健建筑物变形监测方法,利用自适应变步长惯性因子迭代方法对传统PSO算法的惯性因子进行优化,提升全局搜索能力和收敛速度,然后利用改进后的PSO算法对SVM的核参数进行寻优,相对于传统方法具有更高的预测精度,对不同数据具有更强的适应能力和低信噪比条件下的噪声稳健性,通过两例实测数据的试验结果表明:

(1)对于匀速-增速型变形监测数据,PSO-SVM方法相对于传统小波方法和SVM方法在最小误差,最大误差和误差均值三个维度都可以获得最优的预测性能;

(2)对于复杂变化型变形监测数据,PSO-SVM方法相对于传统小波方法和SVM方法在最小误差,最大误差和误差均值三个维度同样可以获得最优的预测性能;

(3)PSO-SVM方法对不同数据类型获得的预测性能较为接近,相对于传统小波方法和SVM方法具有更强的数据适应能力;

(4)传统小波方法和SVM方法的预测性能随着信噪比降低呈现出明显的下降趋势,而PSO-SVM方法在低信噪比条件下的预测性能要远优于上述两种方法,具有更强的噪声稳健性。

综上所述,所提方法在相对于传统小波方法和SVM方法更合适实际工程使用。