注入功率比可调控的双泵浦复合腔501 nm 青光激光器
2021-04-20金光勇
王 兰,金光勇 ,董 渊,王 超
(1.长春理工大学吉林省固体激光技术与应用重点实验室,吉林 长春 130022;2.吉林省计量科学研究院吉林省计量测试仪器与技术重点实验室,吉林 长春 130103)
1 引言
将全固态激光器与非线性频率变换技术相结合,通过倍频或和频获取480~510 nm 波段的激光输出,是目前比较常用的技术手段[1-6],为了在这些波段获得高性能输出,国内外学者做了大量研究[7-9]。早在2006 年,Jacquement[10]等人利用自己研制的Yb:KYW 晶体获取了1 003.4 nm 激光,以此作为基频光,结合一个复杂的环形腔结构,将1 003.4 nm 激光通过KNbO3进行腔内倍频,最终获得35 mW 的501.7 nm 青光输出。由于腔型结构过于复杂,固有损耗过高,因此,获得的青光输出功率不算理想。2012 年,E.J.Hao[11]等人采用复合腔双腔结构,通过在腔中置入1/4 波片等光学元件构成扭摆腔实现了有效的模式选择,成功提高了青光输出功率。2013 年,付喜宏[12]等人通过采用V 型复合腔泵浦复合Nd:YAG 晶体,有效减小了高功率下激光增益介质所产生的热透镜效应,运用Ⅱ类KTP 晶体实现腔内和频,最终获得了730 mW 的500.9 nm 青光输出。该实验再一次证明了复合腔结构结合和频变换技术是获得500 nm 附近青光输出的有效手段。2015 年,Mahmoud Tawfieq[13]等人提出了一个新的概念,利用新型锥形二极管激光器,以978 nm 和1 063 nm作为基频光,获得509 nm 青光输出。光-光转换效率为12.1%。同年Ruijun Lan[14]等人利用Yb:YCOB晶体作为增益介质获得了974 nm 和1 042 nm 谱线的同时振荡,经过Ⅱ类KTP 晶体进行和频,获得503 nm 激光输出。目前对于500 nm 附近青光的研究多集中在采用新晶体、新腔型等方法来获得该波段输出光和提高输出功率上,而对于500 nm附近青光的输出功率以及转换效率的可调控性方面,没有相关研究报道,而有效、稳定的控制光光转换效率以及输出功率,将提高500 nm 附近激光在通讯传输、测深等领域的精准度和深入程度。
为弥补上述研究空白,本文采用双泵浦源复合式腔内结构,理论实验相结合,实现了参与和频变换的基频光之间的无增益竞争,通过调节泵浦功率有效控制复合腔内参与和频变换的注入光功率比,并对和频转换效率和输出功率进行定量调节。以Nd:YAG 和Nd:YVO4作为增益介质,基频光为946 nm 和1 064 nm,经LBO 和频,在基频光注入功率比为1.48∶1 时,实现了最大功率为923 mW 的501 nm 青光输出。
2 理论分析
在非线性频率变换过程中,和频转换效率可以表示为[15]:

式中ni(i=1,2,3)分别表示两束基频光及和频光在晶体中的折射率,ε0为真空介电常数(ε0=8.85×1012F/m),sinc2(∆kl/2)为相位匹配函数,其中∆k为相位失配量,l为晶体长度,c为光速。从上式可以看出,和频转换效率取决于非线性晶体的非线性系数deff、基频光光强I1与I2、相位匹配函数sinc2(Δkl/2)及和频光波长λ3。其中,假设Δk=0,则相位匹配函数sinc2(Δkl/2)为最佳相位匹配。在非线性晶体参数和基频光波段确定的条件下,和频光转换效率主要与基频光光强I1与I2有关。
根据光强的定义[16]I=Φchv/πω2,公式中,Φ表示总的腔内光子数,ω为光斑半径,h为普朗克常量,v为激光频率。假设参与和频变换的两个基频光半径近似相等,通过公式(1)可知,直接影响和频转换效率的因素是光子数。在理想状态下,当两束基频光光子数为1∶1 时,和频转换效率达到最大[15-17],因此,如果想提高和频光转换效率,实现和频光功率的定量输出,可以通过建立腔内功率与基频光光子数间的关系来实现。
根据文献[16]中有关速率方程的内容,可知描述准三能级激光系统运行特性的速率方程为:

此外,还可以通过速率方程得到输出功率与光子数之间的关系:

类似的,描述四能级系统运行特性的速率方程为:


根据输出功率与光子数的关系,同样得到了四能级系统腔内功率与输出功率的表达式:
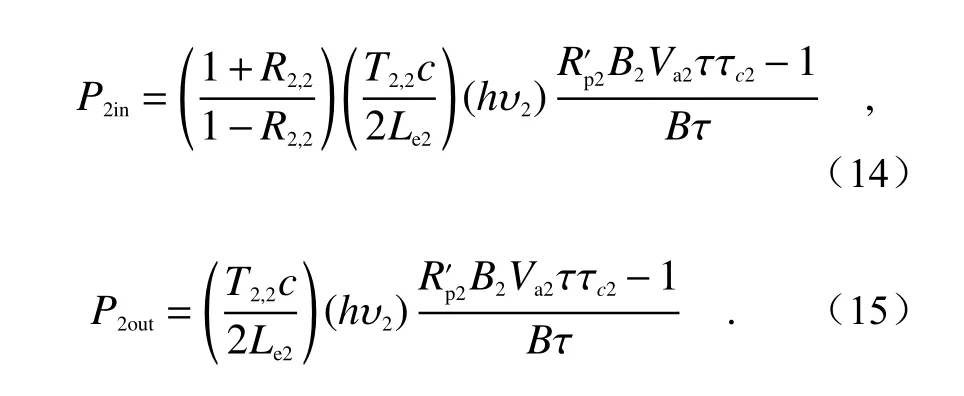
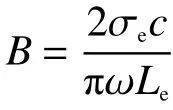
根据上述分析和公式(6),结合本文实验实际参数,得到946 nm 腔内功率和输出功率的表达式如下:

1 064 nm 腔内功率和输出功率表达式如下:

因λ=c/v,当腔内光子数比为1∶1 时,即Φ1064:Φ946=1∶1,公式(5)与公式(13)相等。可以得到两束基频光在和频过程中转换效率最大时与泵浦功率之间的关系,以及两束基频光腔内与腔外功率之间的关系,为和频变换实验过程中定量调节双泵浦注入功率提供理论依据。
3 实验装置及结果分析
本文实验验证了理论模型的正确性,通过避免和频变换过程中增益竞争问题,使参与和频变换的注入功率比具有可控性,实验采用了如图1所示的腔型结构。LD1和LD2是型号为LD-Mate 2V75A-ATPAZ 的808 nm 泵浦源,光纤芯径为400μm,数值孔径为0.22,最大输出功率约35 W。从图1 可以看出,M1,Nd:YAG 和M4构成准三能级946 nm 腔;M2,Nd:YVO4,M3和M4构成1 064 nm腔。M1是曲率P为200 mm 的平凹镜,作为946 nm谐振腔的输入镜,双面镀高透射膜(HT)@808 nm(T>95%),凹面镀高反射膜(HR)@946 nm;M2是曲率P为200 mm 的平凹镜,作为1 064 nm 谐振腔的输入镜,双面镀HT@808 nm(T>95%),凹面镀HR@1 064 nm;M4是整个复合式谐振腔的输出镜,当它作为946 nm 和1 064 nm 基频光输出镜时,前表面镀HT@946 nm(T=2%)&@1 064 nm(T=5%),当它作为501 nm 输出镜时,双面镀HT@501 nm(T>95%),HR@946 nm&1 064 nm(T<2%);M3是45°镜,镀HT@946 nm(T>98%),HR@1 064 nm(T<2%)。Nd:YAG 作为输出946 nm 的增益介质,晶体尺寸为Φ4(mm),高3 mm,掺杂浓度为0.5%,前表面镀HT@808 nm(T>95%),前后表面均镀增透膜(AR)@946 nm(R<0.2%);Nd:YVO4作为输出1 064 nm 的增益介质,晶体尺寸为3 mm×3 mm×5 mm,掺杂浓度为0.3%,前表面镀HT@808 nm(T>95%),前后表面均镀AR@1 064 nm(P<0.2%)。选用LBO 作为非线性和频晶体,相位匹配角为θ=90°,φ=15.4°,晶体尺寸为3 mm×3 mm×10 mm,双面镀AR@1 064 nm(R<0.2%)&946 nm(R<0.5%)&501 nm(R<1%)。谐振腔总长度控制在90 mm 以内。同时获得了946 nm 和1 064 nm 独立输出,用型号为AQ6373 的光谱仪对基频光波长进行采集,如图2 所示。

图1 实验装置示意图Fig.1 Schematic diagram of experimental device

图2 946 nm 和1 064 nm 基频光同时输出光谱图Fig.2 Spectrum of 946 nm and 1 064 nm fundamental frequency laser output at the same time
对理论模型的正确性进行实验验证。结果显示:1 064 nm谐振腔腔长为87 mm,输出镜透过率T=5%;946 nm谐振腔腔长为64 mm,输出镜透过率T=2%。对1 064 nm 和946 nm 输出功率进行测量,并将测得数据代入式(16)、式(18)。通过计算得到可以用来参与非线性和频变换的1 064 nm和946 nm 腔内功率。图3 为946 nm 和1 064 nm输出功率与泵浦电流的关系。图4 为计算得到的946 nm 和1 064 nm 腔内功率与泵浦电流的关系。从图3 和图4 可以看出,1 064 nm 输出功率和腔内可参与和频变换的功率均高于946 nm。
依据理论分析,若使和频转化效率最大,腔内光子数比应满足Φ1064:Φ946=1:1,将式(16)、式(18)代入实际参数,则P946in:P1064in=1.53:1。从理论数据上可以看出,和频变化过程中需要的946 nm 注入功率高于1 064 nm 注入功率,这与谐振腔内946 nm 和1 064 nm 实际功率比相反。因此在非线性和频变换过程中,采取分组实验方式,每组实验首先固定946 nm 腔内参与和频变换的注入功率,对1 064 nm 的注入功率进行满量程范围调节,501 nm 输出功率及和频转换效率达到最大值后均会出现下降,将每组501 nm 输出功率最大值及对应946 nm 和1 064 nm注入光功率比整理如图5、图6(彩图见期刊电子版)所示。
从图5 可以看出,501 nm 输出功率斜效率随着946 nm 和1 064 nm 泵浦功率的增大而增大,最终获得的最大输出功率为923 mW。从图6 可以看出,每组实验中501 nm 输出功率最大时,946 nm 和1 064 nm 注入功率比在2.03∶1 至1.48∶1 之间,946 nm 和1 064 nm 功率都偏低时,注入功率比偏高。这主要是因为低功率时虽然可以进行非线性和频变换但无法保证腔内光子数为1∶1。随着946 nm 和1 064 nm 功率的升高,注入功率比越来越小,501 nm 输出功率斜效率变大,转换效率越来越高;501 nm 输出功率大于800 mW后,946 nm 与1 064 nm 的注入功率比在1.65∶1至1.48∶1 之间,与理论上计算得到的注入功率腔内光子数比为1∶1 时,946 nm 与1 064 nm 的注入功率比为1.53∶1 的理论值基本吻合。为获得非线性和频最大转换效率、最大输出功率对注入光功率的定量调节提供了理论依据和技术手段。图7 为501 nm 光谱图和光斑图。

图3 946 nm 和1 064 nm 输出功率与泵浦电流的关系Fig.3 Relationships between pump current and output power at 946 nm and 1 064 nm

图4 946 nm 和1 064 nm 腔内功率与泵浦电流关系Fig.4 Relationships between the pump current and the intracavity power at 946 nm and 1 064 nm

图5 946 nm 和1 064 nm 泵浦功率与501 nm 输出功率关系Fig.5 Relationship between pump power at 946 nm and 1 064 nm and output power at 501 nm

图6 501 nm 输出功率与946 nm 和1 064 nm 注入功率比的关系Fig.6 Relationship between output power at 501 nm and injection power ratio of 946 nm and 1 064 nm

图7 501 nm 光谱图和光斑图。(a)光谱图;(b)2D 光斑;(c)3D 光斑Fig.7 Spectrum and spot at 501 nm.(a)Spectrogram;(b)2D spot;(c)3D spot
4 结论
本文通过对双泵浦源复合式谐振腔结构中影响和频输出功率和转换效率的相关参数建立理论模型,推算出946 nm 和1 064 nm 腔内功率,及使非线性和频变换转换效率达到最大的条件,腔内光子数为1∶1 时,946 nm 和1 064 nm 注入功率比的理论值为1.53∶1。双泵浦源复合式谐振腔结构避免了两束参与非线性和频变换的基频光之间的增益竞争且具有可调控性,易于增加非线性频率变换次数,从而提高转换效率。通过搭建实验平台对腔型优势和理论模型进行了实验验证,实现了946 nm 和1 064 nm 在复合腔内的无增益竞争及输出,对注入非线性和频晶体LBO 的946 nm和1 064 nm 光功率进行定量调节,最终获得最大输出功率为923 mW 的501 nm 青光,此时的946 nm和1 064 nm 注入功率比为1.48∶1。实验结论与理论分析相吻合。为非线性和频变换技术中通过调控参与和频过程的注入光功率提高和频转换效率提供了理论和技术依据。
猜你喜欢
杂志排行
中国光学的其它文章
- Line-scanning confocal microscopic imaging based on virtual structured modulation
- Enhanced dye-sensitized up-conversion luminescence of neodymium-sensitized multi-shell nanostructures
- Polarization changes of partially-coherent Airy-Gaussian beams in a slanted turbulent atmosphere
- Hybrid plasmonic leaky-mode lasing on subwavelength scale
- 10−9 量级高灵敏度点源透射比测试设备研究
- 大孔径静态干涉成像光谱仪径向畸变导致的谱线偏移误差的校正
