基于黏聚区模型的混凝土细观断裂分析

2021-04-20周正峰康玉峰罗君豪张灏鹏

东南大学学报（自然科学版） 2021年2期

周正峰康玉峰罗君豪张灏鹏

(西南交通大学土木工程学院, 成都 610031)(西南交通大学道路工程四川省重点试验室, 成都 610031)

裂缝是水泥混凝土的主要病害之一.为探究混凝土的开裂机理,研究者们建立了各种基于非线性断裂力学[1-3]和连续损伤力学[4-5]的数值模型,用以模拟混凝土的损伤开裂过程,且大都将混凝土视为均质材料.但从细观尺度来看,混凝土是由水泥砂浆、骨料、骨料-砂浆界面和孔隙组成的一种复合多相材料,其断裂性能与内部相的组成、强度和空间分布密切相关[6-7].因此,分析混凝土细观结构特征对混凝土开裂行为的影响,可以为混凝土细观力学分析提供参考.

随着计算机技术的发展,已有学者基于混凝土细观多相性、随机性和非均质性等特点,建立了混凝土细观模型,用于力学分析.目前,最为常见的混凝土细观建模方法,是基于数字图像的建模和参数化建模.前者运用先进的成像技术(如核磁共振波谱或X射线断层扫描)生成细观结构的数字图像,然后将其转换成具有真实尺寸、形状和分布的有限元网格模型[8-11];但成本较高,耗时较长.参数化建模通常应用间接或直接算法生成细观结构.间接算法是将骨料和砂浆随机分配到模型单元中,并赋予单元不同相属性[12-13].直接算法是在模型空间中随机生成不同形状和尺寸的骨料,再在骨料间隙填充砂浆[14-15];该方法可以模拟骨料颗粒的形状、尺寸、级配、分布以及骨料-砂浆界面等细观特征.

在基于混凝土细观模型的开裂分析中,Taj等[16]、Du等[17]和Zhang等[18]运用扩展有限元方法,分别对四点加载混凝土简支梁、单轴拉伸混凝土试件和三点加载混凝土简支梁的开裂过程进行模拟,发现孔隙的存在会导致混凝土承载力下降,影响断裂能,且骨料与砂浆之间的黏结强度对混凝土的峰值强度影响较大.Permanoon等[19]通过模拟三点加载混凝土梁,发现骨料分布会影响应力强度应子和J积分值.Li等[20]、Peng等[21]基于混凝土塑性损伤模型,分析了四点加载混凝土梁的Ⅰ-Ⅱ型断裂,发现骨料体积分数和粒径大小影响着试件的断裂能和峰值荷载.

在开裂模拟分析中,学者们大多采用基于黏聚区模型的黏结单元来模拟混凝土的细观开裂过程[22-26].黏结单元只能传递法向应力和切向应力,且其几何厚度可设置为任何非负值[27].将黏结单元插入相邻结构单元边界,可以模拟单元界面之间的力学性能以及潜在的开裂面[25-26].

为考虑非均质细观结构对混凝土受力的影响,本文基于ABAQUS软件及黏聚区模型,运用混凝土二维细观建模方法[28],编写了凸多边形骨料和圆形孔隙生成程序,建立了混凝土小梁二维细观模型.通过编写批量插入零厚度黏结单元的子程序,将零厚度黏结单元插入到砂浆内部和骨料-砂浆界面,模拟混凝土内部裂缝的随机萌生和扩展过程.通过对双切缝混凝土小梁试件三点加载断裂全过程的模拟,并与试验结果对比分析,验证了基于黏聚区的细观开裂分析模型的可靠性.在此基础上,分析了孔隙率、骨料体积分数、骨料-砂浆界面强度对混凝土小梁开裂和承载力的影响.

1 混凝土小梁细观有限元模型

1.1 混凝土细观结构的组成

在细观上,混凝土被视为由水泥砂浆、骨料、骨料-砂浆界面和孔隙组成.本文建立二维细观模型时,骨料级配由Fuller级配计算公式确定[29],即

(1)

式中,p(d)为骨料通过筛孔尺寸d的百分数;dm为骨料最大粒径;u为级配指数,在0.45～0.70之间.

将骨料按粒径尺寸分级,第i级骨料面积Si为

(2)

式中,di为第i级筛孔尺寸;ds为骨料最小粒径;Pa为骨料体积分数；S′为混凝土模型面积.

本文采用的混凝土质量配合比见表1[30],骨料级配见表2.粒径小于4.75 mm的细集料与水泥基质一起组成砂浆,混凝土内孔隙假设为圆形,直径dp为2～4 mm[25].

表1 混凝土质量配合比 kg/m3

表2 骨料级配

1.2 混凝土小梁细观结构的生成

混凝土小梁细观结构的生成步骤如下:

1) 生成单个骨料模型.将骨料形状近似为边数3～6的不规则凸多边形.凸多边形骨料模型采用辅助圆内接多边形生成,即

① 确定辅助圆的圆心坐标(xc,yc)为

xc=xmin+λ(xmax-xmin)

(3)

yc=ymin+λ(ymax-ymin)

(4)

式中,λ为0～1之间的随机数;xmin、xmax分别为矩形模型边界横坐标的最小值和最大值;ymin、ymax分别为矩形模型边界纵坐标的最小值和最大值.

② 确定第i级骨料辅助圆半径Ri为

(5)

③ 生成辅助圆内接多边形.根据凸多边形边数,在辅助圆上确定其顶点位置.以不规则凸六边形为例,生成的骨料模型见图1.

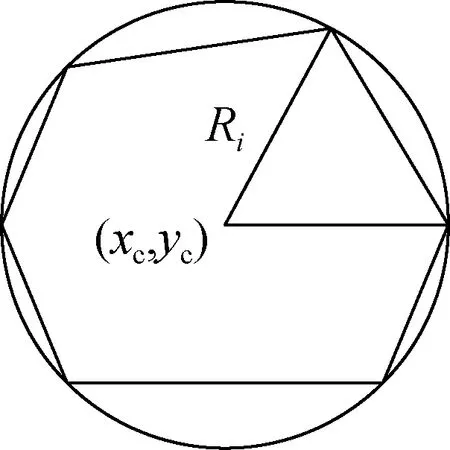
图1 不规则凸多边形骨料模型

2) 生成各档骨料模型.生成后续骨料时,需同时满足:① 整个骨料必须在模型区域内;② 与任何已生成的骨料之间没有重叠;③ 骨料之间的最小距离大于1 mm.若不能同时满足这3个条件,则调整式(3)～(5)中的随机数λ,重新生成骨料.当第i级已生成的骨料面积Ai≥Si时,按表2级配生成下一档骨料,直至所有骨料生成完毕.

3) 生成孔隙.根据孔隙率Pp,将孔隙假想为圆形虚拟骨料,重复步骤1)和2)生成孔隙.砂浆为混凝土梁模型区域中除骨料和孔隙之外的部分.

1.3 黏结单元的批量插入

首先,利用ABAQUS软件对模型剖分网格,生成inp文件.考虑到裂缝在模型内可沿任意路径扩展,需将砂浆和骨料剖分成尺寸很小的三角形单元.

然后,通过子程序修改inp文件,将零厚度黏结单元插入到已网格化的骨料-砂浆界面和砂浆体内部.子程序功能是将单元原始节点复制产生新节点(见图2),再利用新节点生成黏结单元,并重新生成砂浆和骨料单元.新节点的坐标与原始节点相同,即黏结单元的厚度为零.

(a) 原始节点

最后,将子程序修改过的inp文件导入ABAQUS软件进行计算.

2 黏聚区模型的应用

2.1 基于牵引力分离法则的黏结单元本构

黏聚区模型采用ABAQUS软件中基于牵引力分离法则的黏结单元,通过黏结单元的受力来模拟开裂及裂缝扩展.

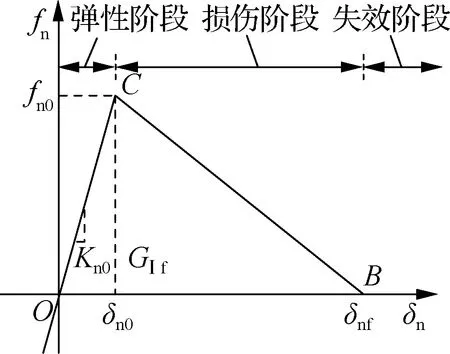
牵引力分离法则实际上表征的是黏结单元2个相对表面之间的法、切向牵引力fn、fs与这2个表面法、切向相对位移δn、δs的关系[27].该法则将黏结单元受力到失效所受的牵引力-相对位移曲线分为弹性、损伤和失效3个阶段(见图3).图中,fn0、fs0分别为黏结单元法、切向产生初始损伤时的牵引力;Kn0、Ks0分别为黏结单元法、切向的初始刚度,即弹性阶段牵引力与相对位移的比值;C点为黏结单元初始损伤点,即弹性阶段和损伤阶段的分界点;δn0、δs0分别为黏结单元法、切向初始损伤点对应的相对位移;δnf、δsf分别为黏结单元法、切向最终失效时的相对位移;GⅠf、GⅡf分别为材料的Ⅰ、Ⅱ型断裂能(即三角形△OBC所围成的面积).在弹性阶段,黏结单元牵引力与相对位移成正比;在损伤阶段,单元软化,牵引力不断减小,相对位移持续增大;当断裂应变能达到单元材料属性时,牵引力变为零,单元进入失效阶段,并形成裂缝.

(a) 法向牵引力-相对位移

(b) 切向牵引力-相对位移

2.2 黏结单元的初始损伤准则

当单元应力满足初始损伤准则时,单元发生初始损伤.本文采用二次名义应力损伤准则,即

(6)

式中,〈〉为Macaulay算子,当算子内数值小于0时计算结果为0,即不考虑单元法向受压损伤.

2.3 黏结单元的损伤演化特征

由图3可知,黏结单元发生损伤后,牵引力会随着相对位移的增加而减小,通过定义损伤变量D来表示单元发生损伤后牵引力的衰减程度.单元发生初始损伤前,损伤变量为0,单元牵引力与相对位移为线性关系;单元发生初始损伤后,损伤变量随相对位移的增加从0到1单调线性增大,单元牵引力逐渐减小,当损伤变量为1时单元牵引力减小为0.

考虑损伤演化过程中法、切向变形的综合作用,引入单元有效相对位移δm,即

(7)

根据图3,推导出损伤变量D的表达式为

(8)

式中,δ0、δf分别为黏结单元初始损伤和失效时的有效相对位移.

发生损伤后牵引力fn、fs可表示为

(9)

(10)

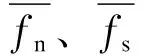
3 小梁细观开裂分析

3.1 小梁加载模型

小梁尺寸为400 mm×100 mm×100 mm,在梁跨中截面和左侧距跨中30 mm处的截面进行预切缝,切缝深度为20 mm,并在跨中施加位移荷载(见图4).

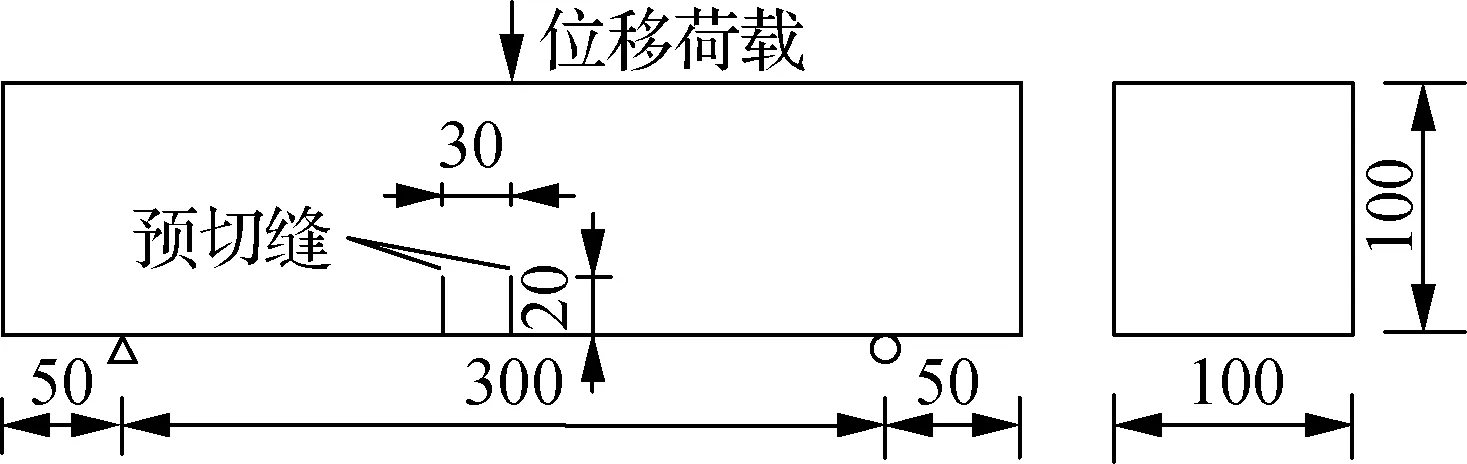
图4 混凝土小梁三点加载示意图(单位:mm)

用第1节中方法生成混凝土小梁细观模型,其中骨料体积分数Pa为43%,孔隙率Pp为0.网格由边长约3 mm的三角形组成,近似考虑裂缝沿任意路径扩展[25-26].砂浆和骨料采用三角形平面应力单元CPS3模拟,并运用黏结单元批量插入子程序,在网格化的砂浆内部和骨料-砂浆界面插入零厚度的黏结单元COH2D4(见图5).图中,红色线条即为插入的零厚度黏结单元.模型材料参数参考文献[30]取值.

图5 黏结单元分布

3.2 模型验证

图6给出了小梁加载力-加载位移曲线数值计算结果与试验结果的对比.由图可知,数值计算得到的承载力峰值与试验值仅相差1.1%,软化阶段加载力-加载位移曲线下降趋势也与试验结果相一致.

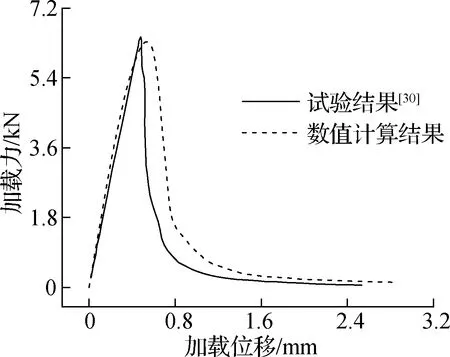
图6 小梁加载力-加载位移曲线

试验中仅中间切缝处发生裂缝扩展,左侧切缝处在整个加载过程中未产生裂缝扩展(见图7).数值模拟的裂缝扩展路径与文献[30]中试验观测到的开裂路径吻合良好,表明基于黏聚区的混凝土细观模型能准确模拟混凝土的开裂.

图7 数值模拟的小梁开裂路径

3.3 裂缝扩展分析

根据跨中切缝处黏结单元的应力状态,将小梁加载力和裂缝扩展消耗的断裂能随加载位移的变化分为弹性阶段Ⅰ、非线性阶段Ⅱ、软化阶段Ⅲ和开裂阶段Ⅳ(见图8).

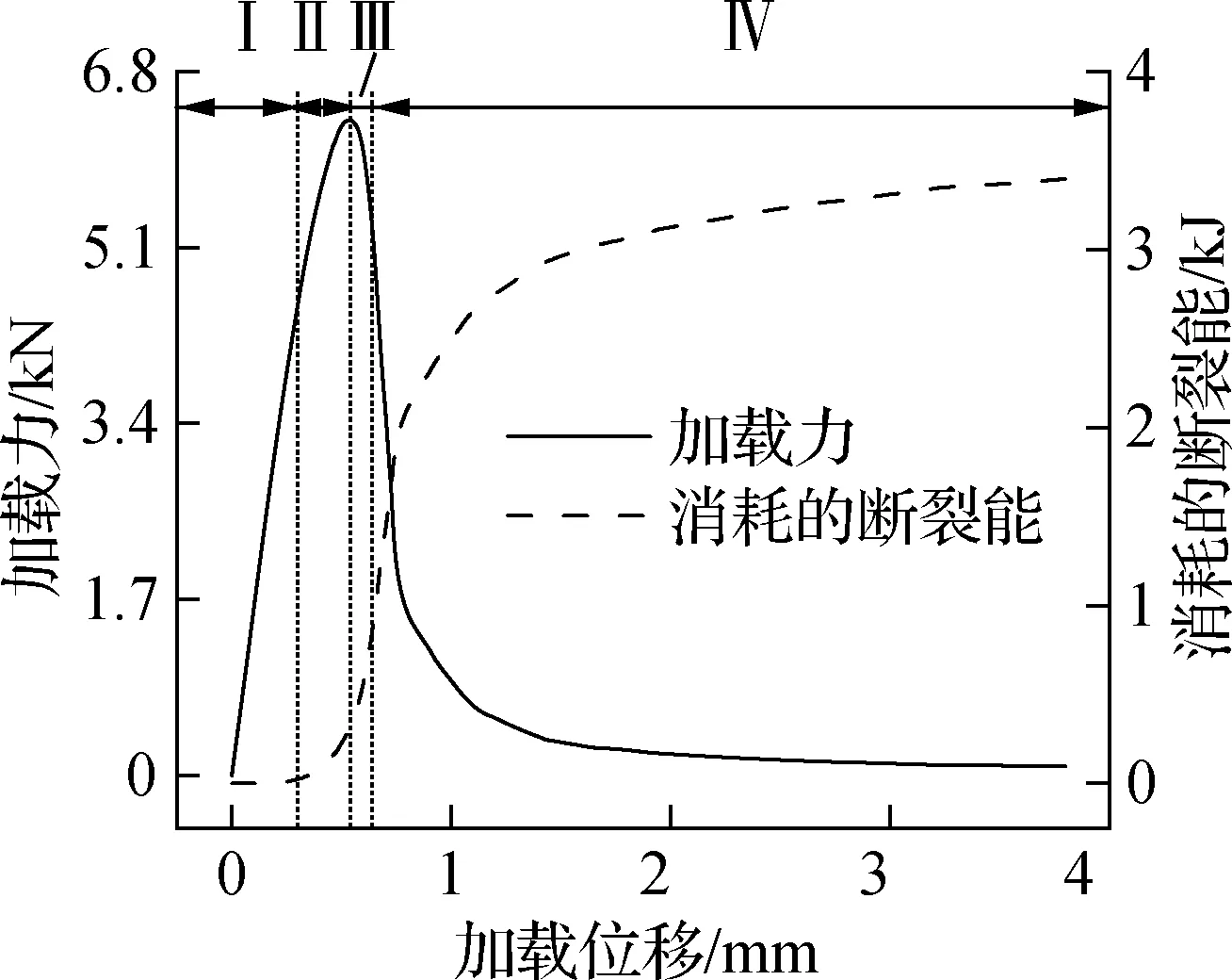
图8 小梁加载力和消耗的断裂能随加载位移变化曲线

图9为加载过程中不同阶段小梁切缝处裂缝形态图.图中,红色单元为受损的黏结单元,表示混凝土中的微裂缝;β为模型放大系数.

(a) 阶段Ⅰ(β=50)

当加载位移较小时,梁底跨中切缝处黏结单元受力小于材料抗拉强度,未发生损伤(见图9(a)),小梁受力处于弹性阶段.加载力随加载位移增加而线性增大,消耗的断裂能为零.当加载位移增大至0.30 mm时,对应的加载力为使小梁处于弹性工作状态的临界荷载.

当加载位移大于0.30 mm时,随着加载位移的继续增大,梁底跨中切缝处黏结单元达到材料抗拉强度,黏结单元开始出现损伤(见图9(b)),应力发生重分布,小梁受力进入非线性阶段.但由于小梁截面上受较大拉应力的区域面积增大,小梁的承载力继续增加.当加载位移增大至0.54 mm时,小梁承受荷载达到峰值6.33 kN,为弹性工作状态临界荷载的1.4倍,此时消耗的断裂能为0.31 kJ.

当加载位移大于0.54 mm时,随着加载位移进一步增大,梁底跨中切缝处产生损伤的黏结单元不断增多(见图9(c)),小梁承受的荷载不断减小,进入软化阶段.当加载位移增大至0.64 mm时,梁底跨中切缝处的黏结单元达到断裂能并失效,此时小梁承受的荷载为荷载峰值的0.84,为弹性工作状态临界荷载的1.16倍.

当加载位移大于0.64 mm时,随着加载位移的进一步增大,梁底跨中切缝处失效的黏结单元不断增多(见图9(d)),小梁进入开裂阶段.跨中切缝处出现宏观裂缝,加载力-加载位移曲线下降速率加快,消耗的断裂能急剧增加,最终在小梁跨中形成从下而上的贯穿裂缝.

4 细观结构的影响分析

在小梁细观模型基础上,分析孔隙率、骨料体积分数和骨料-砂浆界面强度等混凝土细观结构特征对小梁开裂以及承载力的影响.

4.1 孔隙率的影响

孔隙率Pp分别取2%、4%、6%,其他模型参数不变,分析孔隙率对小梁结构受力的影响,结果见图10.

(a) Pp=2%

(b) Pp=4%

图11为不同孔隙率下的小梁加载力-加载位移曲线.由图可知,随着孔隙率的增大,加载力-加载位移曲线的初始斜率逐渐减小,即小梁初始刚度降低;加载力峰值也明显减小,即小梁极限承载力降低.当孔隙率从0增大到6%时,小梁极限承载力降低了24.5%，这表明孔隙率增加会使小梁抵抗弯拉作用的有效面积减少,从而导致小梁的初始刚度和极限承载力降低.

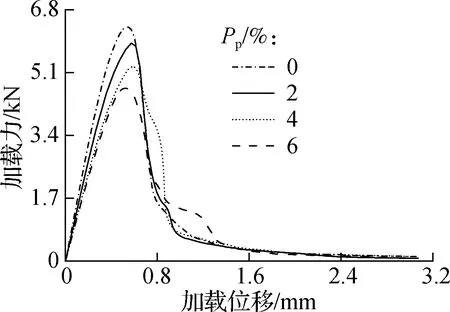
图11 不同孔隙率下小梁的加载力-加载位移曲线

图12为不同孔隙率下小梁的开裂路径.图中,红色虚线为小梁的跨中轴线.由图可知,孔隙相当于小梁结构内部的薄弱面.随着孔隙的增多,孔隙周边逐渐出现应力集中的现象,使得小梁裂缝从跨中切缝开始沿着孔隙较多的路径扩展.

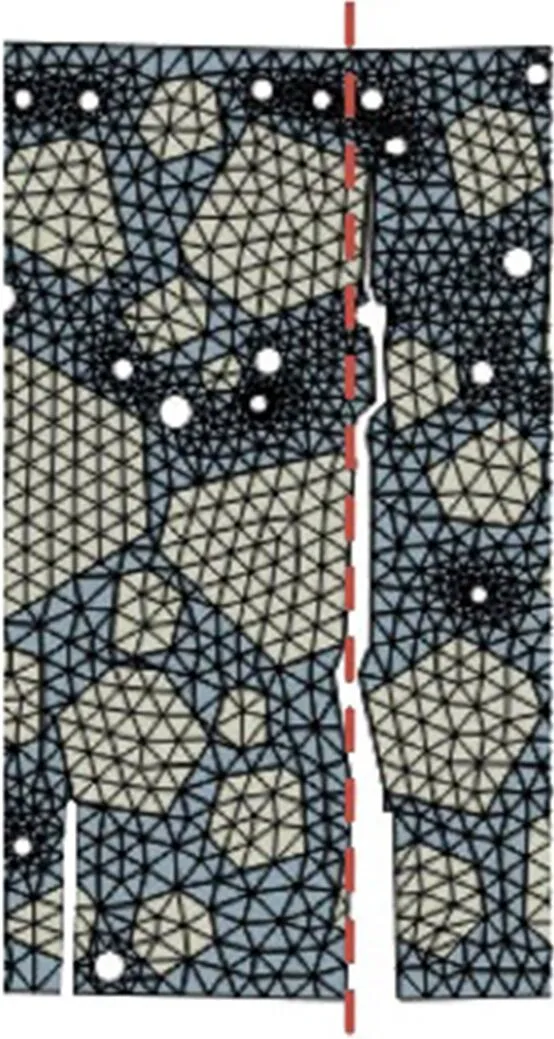
(a) Pp=2%

4.2 骨料体积分数的影响

骨料体积分数Pa分别取20%、30%、40%和50%,其他模型参数不变,分析骨料体积分数对小梁结构受力的影响,结果见图13.

(a) Pa=20%

(b) Pa=30%

(d) Pa=50%

图14为不同骨料体积分数下小梁的加载力-加载位移曲线.由图可知,随着骨料体积分数的增大,小梁初始刚度和极限承载力增大,骨料-砂浆界面面积增大,开裂所需消耗的断裂能也增加.当骨料体积分数从20%增大到50%时,小梁极限承载力增大了17.4%,小梁达到极限荷载和形成宏观裂缝时所消耗的断裂能Gd1、Gd2分别增加了54.3%和62.7%(见图15).

图14 不同骨料体积分数下小梁的加载力-加载位移曲线

图15 不同骨料体积分数下小梁消耗的断裂能

4.3 骨料-砂浆界面强度的影响

骨料-砂浆界面强度f0z分别取为砂浆强度的40%、60%、80%、100%,其他模型参数不变,分析骨料-砂浆界面强度对小梁结构受力的影响,结果见图16.由于骨料-砂浆界面强度小于砂浆强度,小梁开裂及裂缝扩展主要出现在骨料-砂浆界面,骨料-砂浆界面强度也就决定了小梁极限承载力.由图可知,骨料-砂浆界面强度从1.24 MPa增大到3.10 MPa时,小梁极限承载力增大了30.3%,且小梁的极限承载力随骨料-砂浆界面强度的增加几乎呈线性增长.