地铁线路先锋扣件结构参数对轮轨摩擦自激振动的影响*

崔晓璐 程 梽 何志强 漆 伟

(1.重庆交通大学机电与车辆工程学院 重庆 400074； 2.重庆市轨道交通(集团)有限公司 重庆 401120)

城市轨道车辆以安全、高效、运量大、绿色环保等特点得到了快速发展，虽有效缓解了城市的交通压力，但却带来了新的问题，比如列车运营时产生的振动噪声，不仅对沿线居民的居住环境和建筑造成影响，严重时还会导致脱轨事故发生[1-2]。为缓解地铁振动噪声问题，某些地铁线路采用了先锋扣件、科隆蛋扣件等减振支撑结构。然而这些结构在取得减振成效的同时也带来严重的钢轨波磨，反而加剧了车辆运行时的振动与噪声，并严重降低了钢轨和车辆零部件的使用寿命[3-6]。钢轨波磨作为轮轨接触问题中的普遍现象，是一种沿钢轨接触表面出现的周期性的类似于波浪型的非均匀磨损现象[7]。对于钢轨波磨的研究，主要从波长固定机制和损伤机制2个方面展开[8]。其中波长固定机制主要分为以下2种理论[9-12]：(1)轮轨瞬态动力学相互作用引起摩擦功波动导致钢轨波磨理论,该观点认为钢轨存在初始不平顺，当列车通过不平顺时，会诱导轮轨系统产生不稳定振动，从而引发钢轨波磨产生;(2)轮-轨黏滑自激振动导致钢轨波磨理论。

轨道支撑结构对地铁线路的减振具有重要影响，基于钢轨波磨的基本理论，研究者们对轨道支撑结构参数对波磨的影响展开一系列的研究工作。李伟等人[13-14]建立科隆蛋扣件支撑的轨道有限元模型，分析结果表明不同的扣件刚度阻尼下的轨道振动特性对钢轨波磨的影响不同，增大扣件刚度阻尼可以有效抑制钢轨波磨产生。OYARZABAL等[15]通过频域波磨模型发现轨垫横向刚度、轨垫垂向刚度、道床垂向刚度、轨枕质量以及轨枕间距这5个参数对钢轨波磨具有明显的影响。EGANA等[16]通过现场调查和数值分析发现，低刚度的轨垫可以减缓钢轨波磨。EADIE等[17]基于黏滑自激振动理论研制出一种摩擦调节器，该装置可以有效缓解钢轨波磨并能很好地控制地铁线路的曲线啸叫。目前地铁线路已将先锋扣件和科隆蛋扣件作为常用的减振结构，然而在北京地铁线路和广州地铁线路的减振区段均出现严重的钢轨波磨。为了进一步研究典型减振轨道结构的波磨问题，本文作者基于轮轨摩擦自激振动导致波磨的理论[18]建立了地铁线路先锋扣件支撑曲线轨道的车辆-轨道系统动力学模型和导向轮轨-钢轨系统的有限元模型，分析了先锋扣件支撑小半径曲线轨道轮轨间的蠕滑状态和轮轨系统的摩擦自激振动特性，并通过参数化分析研究了不同轨道支撑结构参数对轮轨摩擦自激振动的影响，提出抑制钢轨波磨的相关措施。

1 仿真模型与分析方法

1.1 车辆-轨道动力学模型

通过文献检索和现场调研发现在地铁线路先锋扣件支撑段出现了严重钢轨波磨，特别在小半径曲线段，波磨尤为严重[19]。为研究该线路段的波磨，建立了先锋扣件支撑小半径曲线轨道的车辆-轨道动力学模型，如图1所示。轨道曲线半径设为390 m，圆曲线长度300 m，缓和曲线长度120 m，直线长度100 m，轨道超高为0.119 m[20]。

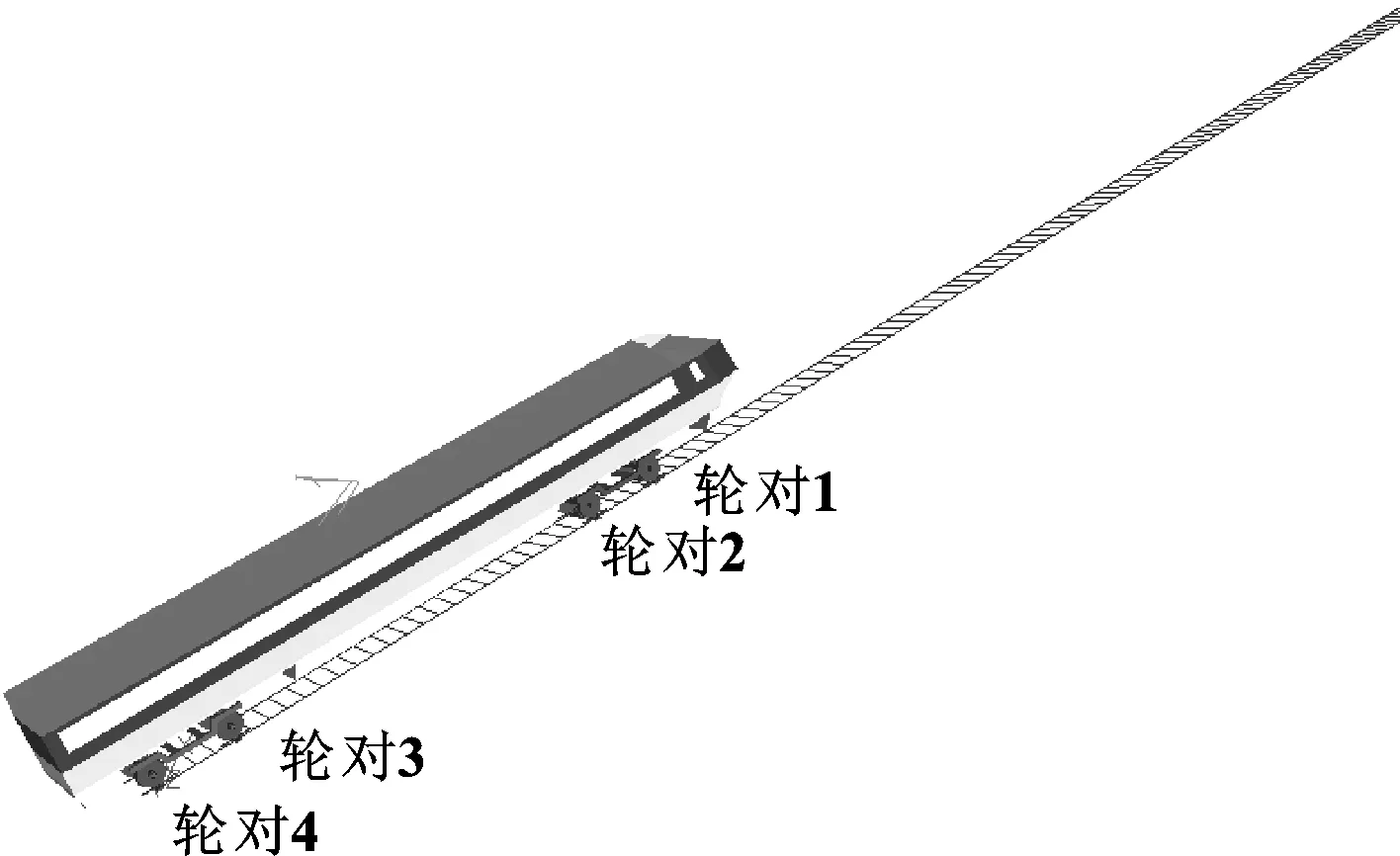
图1 车辆-轨道系统多体动力学模型

根据动力学分析可以计算得到轮对两端的受力情况和轮轨间的接触情况，轮轨系统的接触模型示意图如图2所示。在小半径曲线轨道上，外侧轮对的一系垂向力和横向力分别为FSVL、FSLL，内侧轮对的一系垂向力和横向力分别为FSVR、FSLR。外轮与钢轨的接触点位于轮缘与轨头之间，其接触角为δL,内轮与钢轨的接触点位于踏面与轨头之间，其接触角为δR。外轮与内轮的法向力分别为NL、NR,外轮与内轮的蠕滑力分别为FL、FR。钢轨通过先锋扣件与轨道板连接，先锋扣件的垂向刚度和垂向阻尼分别为KRV、CRV，横向刚度和横向阻尼分别为KRL、CRL。轨道板与地基之间的垂向刚度和垂向阻尼分别为KF和CF。

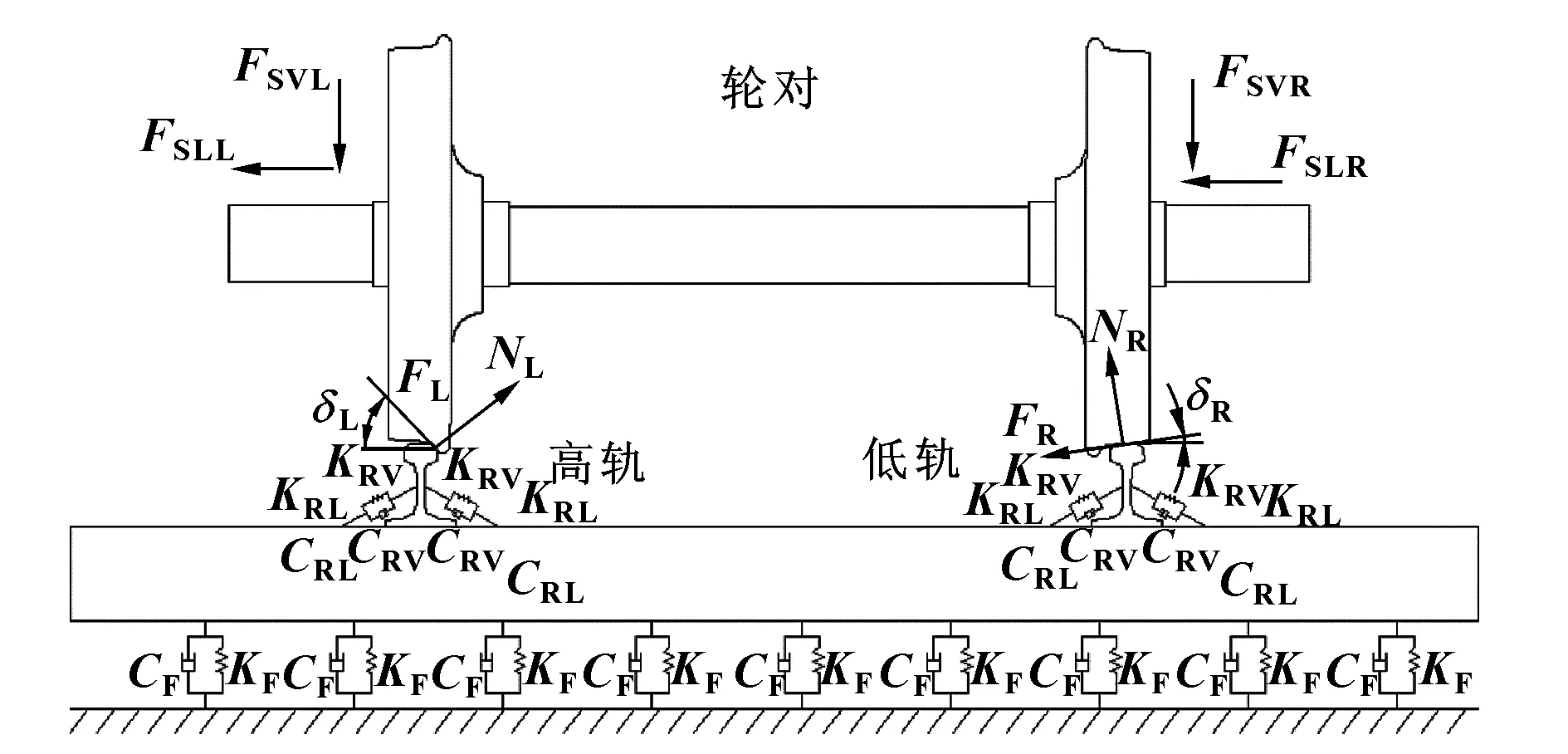
图2 先锋扣件支撑曲线段轮对-钢轨系统接触模型

1.2 导向轮对-钢轨有限元模型

根据车辆-轨道动力学模型和轮轨系统接触模型可以建立相应的轮对-钢轨系统有限元模型，如图3所示，模型的材料参数见表1。由于导向轮对对波磨的影响最为明显，因此仅建立了导向轮对，即车辆-轨道动力学模型中的轮对1。由于先锋扣件轨枕预埋于轨道板内部，因此建立模型时可以将轨枕与轨道板看成一个整体，整个模型由导向轮对、钢轨、轨枕和整体道床组成。轮对采用LM型，直径为840 mm，车轮与车轴之间采取过盈配合，车轴两端采用6个自由度全约束。当车轴受到垂向载荷和横向载荷时，逐步取消车轴的垂向平移约束和横向平移约束。

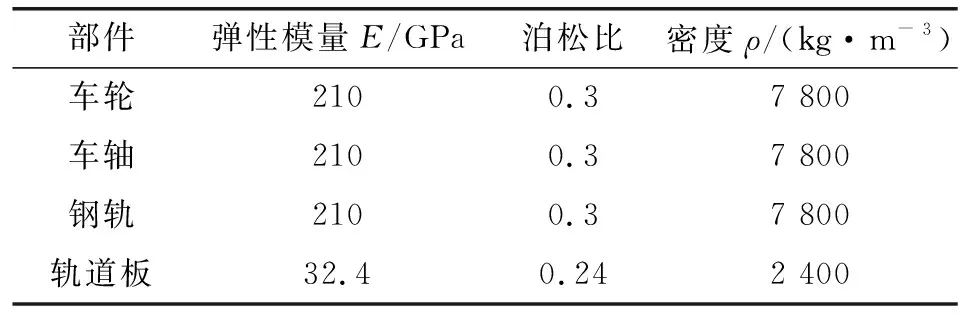
表1 轮对-轨道模型材料参数值

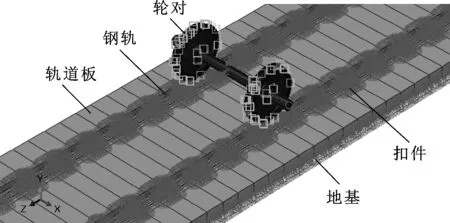
图3 先锋扣件支撑曲线段导向轮对-轨道有限元模型

轮对与钢轨的接触位置通过车辆-轨道动力学分析计算可得，接触摩擦因数μ为0.4。钢轨长度设为30个轨枕跨距，两端采用固定约束，轨枕跨距为625 mm。钢轨和轨枕间采用先锋扣件连接，先锋扣件结构参数如表2所示。先锋扣件采用点对点的弹簧和阻尼单元模拟，由于建立点对点弹簧阻尼工作量比较大，因此采用命令行接口，通过编译Python脚本程序，使其自动批量生成。地基对轨道板的支撑采用点对面的弹簧和阻尼单元模拟。

表2 先锋扣件轨道支撑段结构参数

1.3 摩擦自激振动有限元分析方法

根据建立的轮轨系统有限元模型，可以采用ABAQUS内置的复特征值分析法研究轮轨系统的摩擦自激振动特性。复特征值分析法作为一种常用的分析摩擦自激振动的方法，通过建立轮轨系统的运动方程并求解，根据复特征值的实部判断系统的不稳定频率以及不稳定发生的可能性，理论过程如下[21]。首先建立轮轨系统的运动方程：

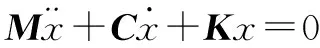
(1)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x为节点位移向量。

刚度矩阵和阻尼矩阵由于摩擦力的引入变为非对称矩阵，不对称程度越大，系统发生不稳定振动的可能性也越大。通过对运动方程的求解，其通解如下所示：

(2)

式中:αk+jwk为系统的第k阶特征值;αk是特征值实部。

当复特征值的实部为负值时，系统趋于稳定，当实部为正值时，系统趋于不稳定，并且实部越大，系统不稳定振动发生的可能性也越大。文中采用复特征值法分析轮轨系统的摩擦自激振动，计算得到轮轨系统的复特征值实部以及相应的振动频率，通过实部的大小，判断轮轨系统产生摩擦自激振动的可能性，进而判断波磨发生的可能性。

1.4 钢轨波磨摩擦功理论

基于轮轨摩擦自激振动导致钢轨波磨的研究，可知摩擦功波动是引起钢轨波磨的关键因素。为探究轮轨摩擦自激振动与摩擦功的关系，文中采用BROCKLEY提出的钢轨波磨理论[22]。理论过程如下：

V=K(H-C)

(3)

式中：V为单位时间内钢轨表面的磨损体积；K为磨损常数；H为摩擦功，H=Fv，F为饱和蠕滑力，v为相对速度;C为长时摩擦功。

将K和C设为常数，当摩擦功波动时，磨损体积也会产生相应的变化。

在小半径曲线轨道时，外轮与内轮的蠕滑力达到饱和，饱和蠕滑力F=μN，μ为接触系数，N为轮轨间的法向力。当蠕滑力达到饱和时，轮轨系统将产生摩擦自激振动，引起法向力产生波动，导致摩擦功产生相同频率的波动。根据公式(3)可知，当轮轨系统产生摩擦自激振动时，单位时间内钢轨表面的磨损体积也会产生相同频率的振动，最终导致波磨的发生。

2 结果与讨论

2.1 车辆-轨道系统的动力学分析

通过SIMPACK的动力学分析可以计算得到车辆通过先锋扣件支撑曲线段轮对的一系悬挂力、蠕滑力以及法向力，其中导向轮对1的受力情况如图4、5和6所示。可以发现,时间区段为17～20 s时，轮轨系统一系悬挂力、蠕滑力以及法向力的数值曲线较为平滑，该区间为列车通过小半径曲线轨道的稳定区间，因此选取该区间内各个参数的平均值作为各个力的数值结果进行研究。其中一系悬挂力用于轮轨系统复特征值分析时轮对两端悬挂力的加载，蠕滑力和法向力用于判断轮轨系统的蠕滑力是否达到饱和。为便于判断轮轨系统蠕滑力是否达到饱和，这里引入黏着饱和系数λ，其定义式如下：

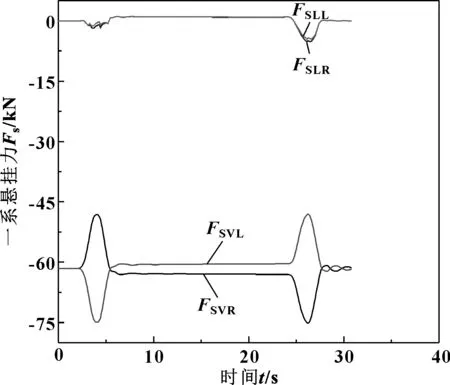
图4 轮轨间一系悬挂力变化曲线

λ=F/(μN)

(4)

式中：F为蠕滑力;μ为接触系数;N为法向力。

当λ等于1时，轮轨系统的蠕滑力达到饱和，当λ小于1时，轮轨系统的蠕滑力未达到饱和。

通过计算可以知道黏着饱和系数随时间的变化趋势如图7所示，其中λR为内轮的黏着饱和系数，λL为外轮的黏着饱和系数。可知,内轮与外轮的黏着饱和系数在稳定区间时，数值接近于1，可以认为车辆通过先锋扣件支撑小半径曲线轨道时，轮轨系统的内轮与外轮的蠕滑力趋于饱和。

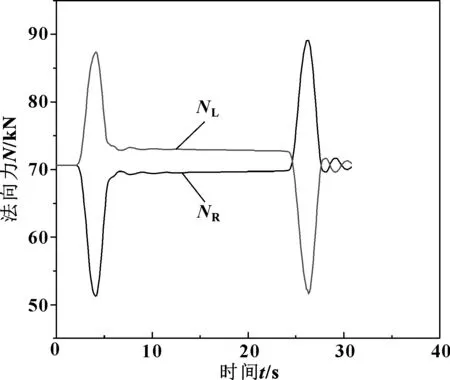
图5 轮轨间法向接触力变化曲线

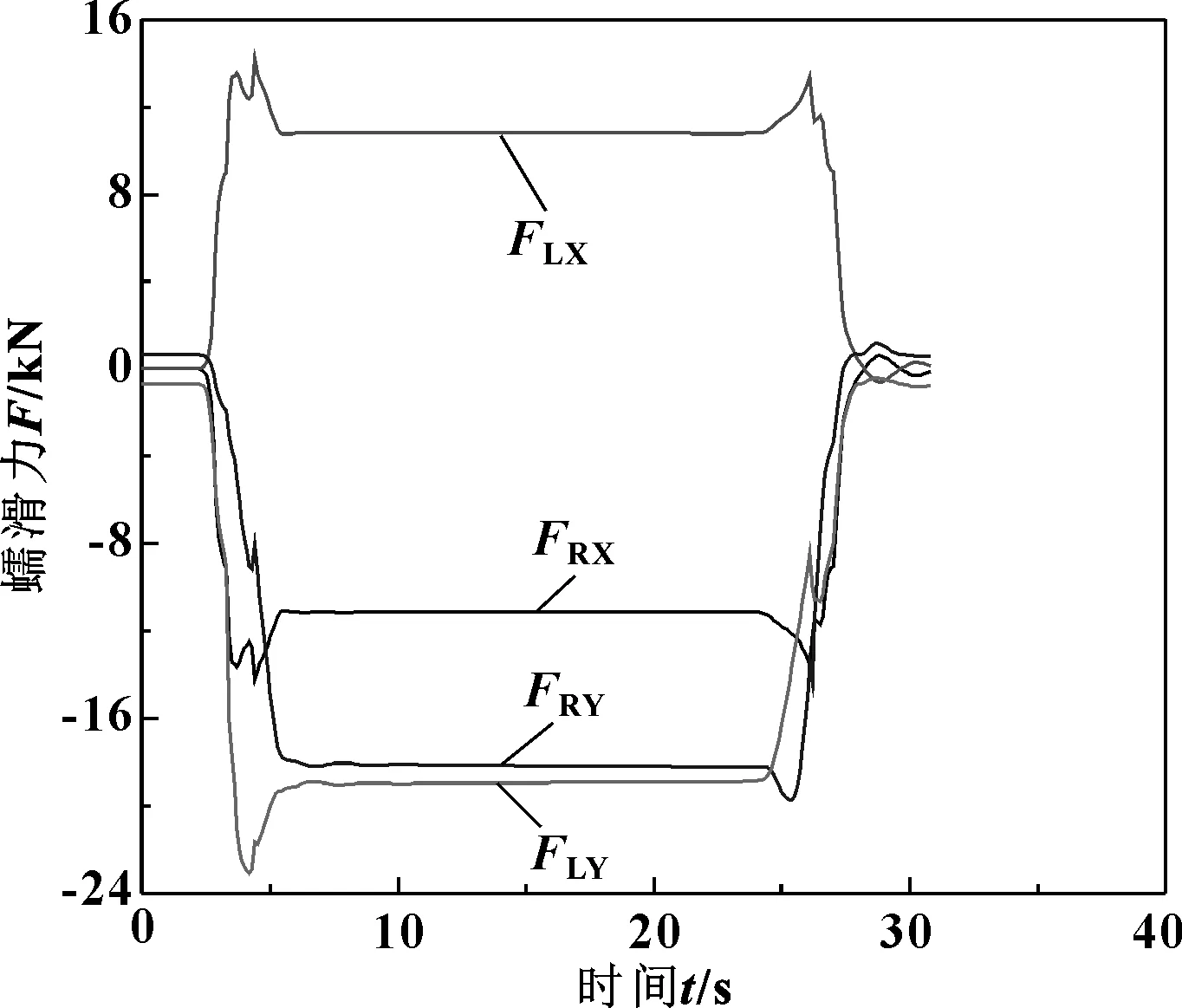
图6 轮轨间蠕滑力变化曲线

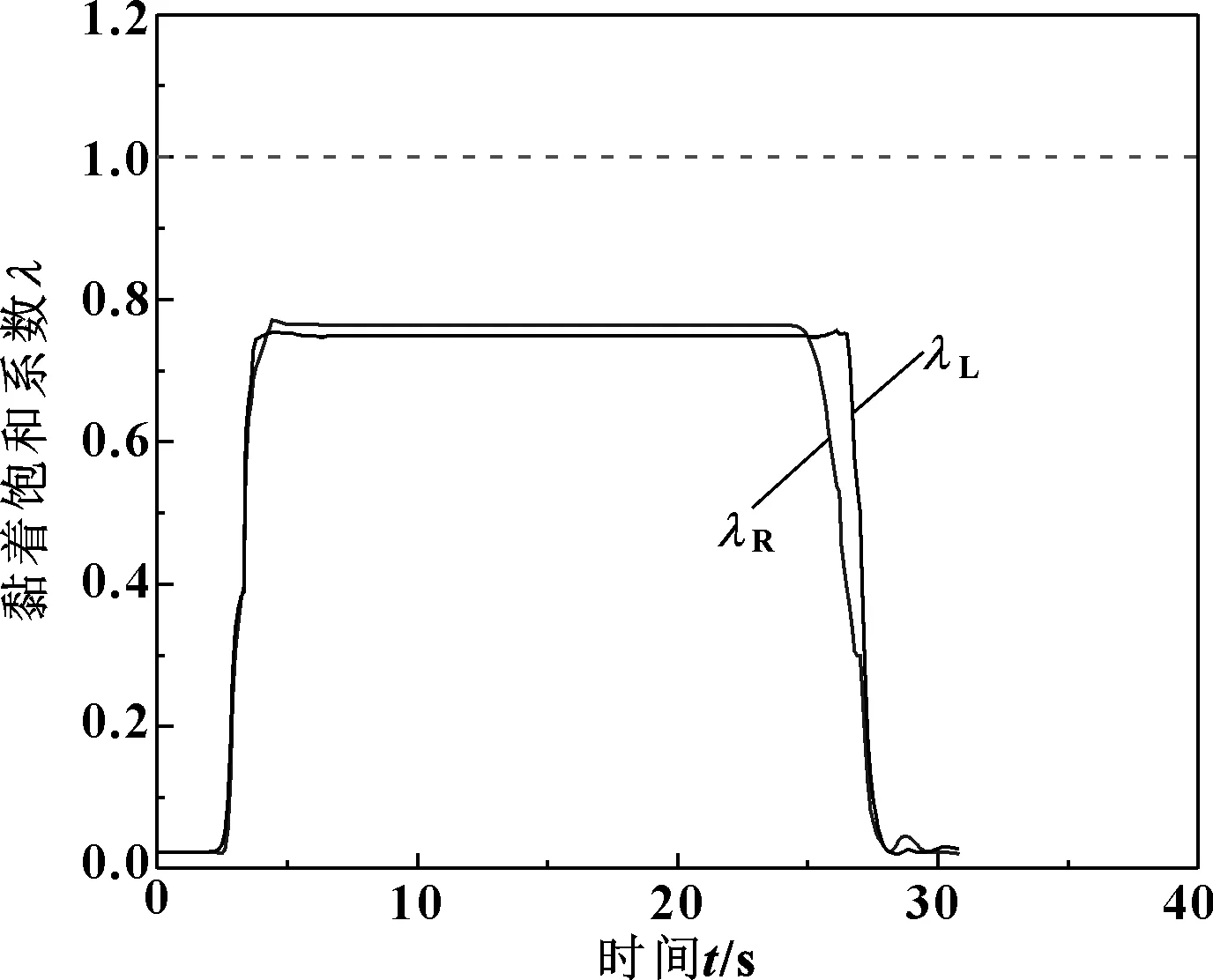
图7 黏着饱和系数变化曲线

2.2 轮轨系统的钢轨波磨分析

通过现场调研发现，在先锋扣件支撑的小半径曲线段出现了波长为30～40 mm的钢轨波磨，列车在该区段上的行驶速度为100 km/h[23]。根据频率公式f=v/λ(v为列车行驶速度，λ为波磨波长)，可以推导出引起该区段钢轨波磨的振动频率为694～926 Hz。通过复特征值分析可以得出先锋扣件支撑小半径曲线轨道导向轮对-钢轨系统的摩擦自激振动频率，如图8所示。

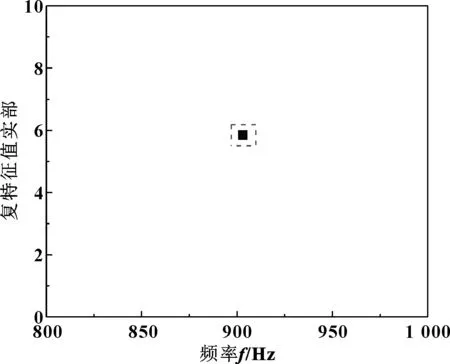
图8 先锋扣件支撑小半径曲线轨道轮轨系统的摩擦自激振动频率

从图8可知，轮轨系统存在903 Hz的摩擦自激振动频率，相应的复特征值实部约为5.9。该摩擦自激振动频率会引起轮轨间法向力产生相同频率振动。根据钢轨波磨摩擦功分析理论可知，波动的法向力会导致摩擦功产生相同频率的波动，最终导致波磨产生。由频率公式可以推导出，不稳定振动频率为903 Hz时，预测得到的波磨波长为30 mm。该频率对应的模态振型如图9所示，可以发现轮轨摩擦自激振动发生在内轨上。综上可知，先锋扣件支撑小半径曲线轨道轮轨系统会产生903 Hz的摩擦自激振动，由此诱发的波磨波长为30 mm，且发生在内轨上，这与实际调研结果相符合，验证了建立的导向轮对-钢轨有限元模型的正确性。

图9 先锋扣件支撑小半径曲线轨道轮轨系统的摩擦自激振动模态

2.3 扣件结构参数对钢轨波磨的影响

由于不同的地铁线路区段所需的减振效果不同，因此相应的轨道支撑结构参数也不相同。文中基于轮轨系统摩擦自激振动的分析结果，以地铁先锋扣件支撑小半径曲线轨道的轮轨系统为研究对象，研究了扣件结构的各个参数对轮轨系统摩擦自激振动的影响情况。这里选取扣件垂向刚度、扣件垂向阻尼、扣件横向刚度、扣件横向阻尼、扣件纵向刚度、扣件纵向阻尼这6个影响参数。根据现场调研结果可以得到这6个扣件结构参数的变化范围，如表3所示[24]。通常假设扣件的横向刚度和纵向刚度一致，横向阻尼和纵向阻尼一致。由于扣件横向刚度和纵向刚度数值保持一致[2,24]，因此在研究中其变化趋势保持一致。

表3 先锋扣件结构参数变化范围

进而，采用控制变量法研究扣件结构参数对钢轨波磨的影响。首先，选取扣件有限元模型初始值(KRY= 5 MN/m，KRX=KRZ=10 MN/m，CRY=10 kN·s/m，CRX=CRZ= 2 kN·s/m)为控制变量初始值。然后，固定控制变量并改变单个变量值，接着采用复特征值法研究单个参数变化时不同变量对轮轨系统摩擦自激振动的影响情况，如图10所示。

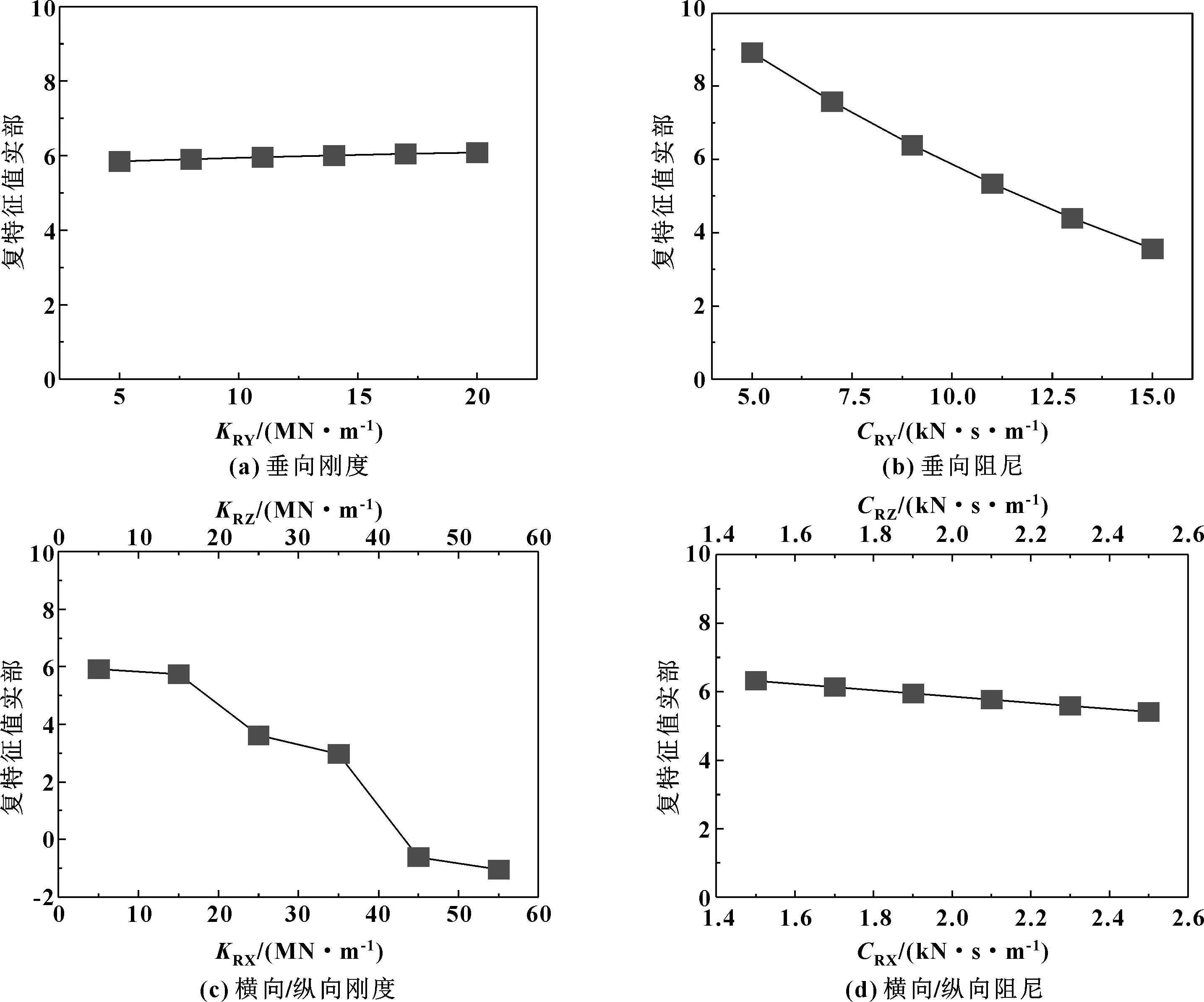
图10 扣件结构参数对轮轨摩擦自激振动影响规律

通过研究发现，在不同扣件参数时，轮轨系统均有约为900 Hz的摩擦自激振动产生。这里通过复特征值的实部大小来判断系统产生不稳定振动的可能性，复特征值实部越大，在该频率下轮轨系统越容易产生摩擦自激振动，钢轨出现波磨的可能性就越大[25]。

从图10(a)可以发现,随着扣件垂向刚度的增加，复特征值的实部变化不明显，仅轻微增大。从图10(b)可以发现，随着扣件垂向阻尼的增加，复特征值实部明显降低，这意味着轮轨系统摩擦自激振动产生的可能性随着扣件垂向阻尼的增加明显下降。从图10(c)可知，随着扣件横向/纵向刚度的增加，复特征值实部明显降低，这意味着轮轨系统摩擦自激振动产生的可能性随扣件横向/纵向刚度的增加明显下降。从图10(d)可知，随着横向/纵向阻尼的增加，复特征值实部降低，这意味着轮轨系统摩擦自激振动发生的可能性随着扣件横向/纵向阻尼的增加而下降。综上所述，根据扣件的参数化分析可以发现，在一定范围内增大先锋扣件的垂向阻尼，增大扣件的横向刚度和横向阻尼有助于抑制轮轨系统摩擦自激振动的产生。

3 结论

(1)基于动力学模型建立相应的导向轮对-钢轨有限元模型，通过对复特征值分析，得到先锋扣件支撑小半径曲线轨道钢轨的不稳定振动频率。该频率与实际调研结果相符合，验证了建立的模型的正确性。

(2)研究轨道支撑结构中扣件的结构参数对轮轨系统不稳定振动的影响规律，结果表明：当列车通过先锋扣件支撑小半径曲线轨道时，导向轮对内外车轮间的蠕滑力趋于饱和，容易诱导轮轨系统产生摩擦自激振动；轮轨系统的摩擦自激振动的主频与诱导波磨的频率接近，这意味着轮轨系统摩擦自激振动频率与波磨密切相关；在一定范围内，先锋扣件垂向阻尼越大，扣件横向刚度越大，扣件横向阻尼越大，轮轨系统摩擦自激振动发生的可能性越小，从而使波磨发生的可能性越小。