轴承温度对托索轮部件配合面变形的影响

黄 山 李 刚 闫登华 李 村 马 胤

北京起重运输机械设计研究院有限公司 北京 100007

0 引言

轴承是客运索道托压索轮中的重要支撑基础件，其能否安全稳定运行直接影响索道线路的安全性与可靠性。在索道检修中,发现轴承在轮体内打滑的现象时有发生，造成这种现象的原因通常有配合选取不当、加工精度不高、结构运转变形等因素。由于轴承在轮体中所处的环境较为封闭，散热条件不佳，在较长时间高速运转后，温度不可避免地会升高，在载荷和温度的双重作用下，不仅影响轴承本身的性能，也会影响相关结构的配合精度，进而影响整体结构的功能和运行质量。

图1 为托索轮结构示意图，主要由轮体、轴承、夹板、端盖、隔套等结构组成，当索道运行较长时间后，轴承温度会升高，而从图1 可以看到，轴承的散热条件相对较差，由于轴承与轮体内圈和隔套均有配合要求，故需要考虑轴承温升对各部件间配合的影响。

本文将通过对轴承发热量的计算，在Ansys 中模拟得到其最高温度，并将轴承作为热源，分析常温环境（20℃）下与轴承有配合关系的部件在受到温度影响时的变形以及配合面接触状态的变化，为设计工作选取合理的公差配合提供参考。

图1 托索轮结构示意图

1 轴承摩擦与温升计算

1.1 轴承摩擦力矩的近似计算

滚动轴承产生热量的多少取决于轴承内的摩擦，而摩擦的大小受到包括轴承类型和尺寸、转速、润滑剂的特性和用量等因素的影响[1]。

轴承部件之间的滚动和滑动摩擦会阻碍轴承转动，滚动体与滚道、保持架以及引导面之间的接触均会产生摩擦阻力。此外，由于润滑剂拖曳和接触式密封件的存在也会产生摩擦。轴承的摩擦力矩为

式中：M 为轴承摩擦力矩，μ 为轴承摩擦系数，F为轴承载荷，d 为轴承内径。

1.2 轴承的温升

轴承摩擦损失在轴承内部几乎都转变为热量，使轴承温度上升，单位时间内摩擦产生的热量为

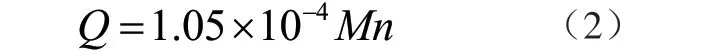
式中：Q 为单位时间内的发热量，M 为摩擦力矩，n 为轴承转速。

1.3 轴承温度的有限元计算

为便于计算，在有限元计算中省去了轴承的密封圈和保持架[2]，但在传热系数的设置上考虑了密封圈对散热的影响。根据式（1）、式（2）计算得到轴承单位时间内的发热量Q=8 W，如图2 所示，（a）为轴承模型，（b）为轴承温度云图，最高温度可达80℃。

图2 轴承模型和温度云图

由图2 可知，在散热条件受限的情况下，轴承内外圈最高温度均接近整体的最高温度，因此在整个轮体计算中，可将轴承设置为一个恒温热源，分析其温度大小对托索轮其他结构的影响。

2 温度对各部件变形影响

图3 为托索轮结构示意图，模型中包含了与轴承直接接触的轮体和隔套（以一根实心轴代替）。轮体材料为ZL104，其余结构材料为钢。ZL104 合金密度2 650 kg/m3，20℃～100℃时的线膨胀系数为24×10-6℃-1，钢的线胀系数为12×10-6℃-1。

图3 整体模型示意图

2.1 部件计算

首先单独计算轮体、轴承和轴在常温环境（20℃）下升温过程（温度梯度设为10℃）中的变形情况，如图4 所示。

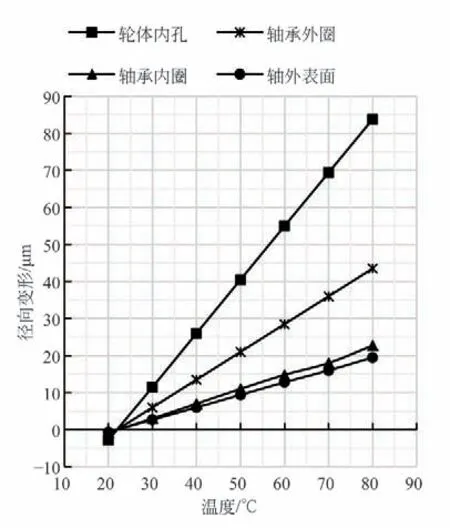
图4 各部件单独计算时的径向变形

由图4 可知，随着温度的升高，各部件径向变形逐渐增加，各配合面中，轮体内孔变形最大，轴的外表面变形最小，轴承外圈变形大于内圈。由于轮体材料的线膨胀系数较钢材大，故轮体内孔径向变形较大。

为对比轮体内圈厚度对径向变形的影响，建立不同内圈厚度的轮体模型，计算其径向变形，如图5 所示。

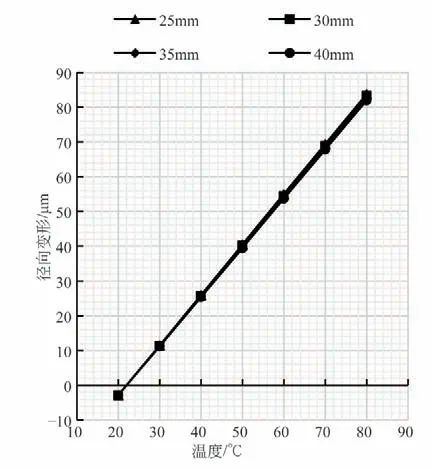
图5 轮体内圈不同厚度下的径向变形

由图5 可知，改变轮体内圈厚度对其径向变形的影响很小，可以忽略不计，故不再考虑轮体内圈厚度对其径向变形的影响。

2.2 整体计算与单独计算的对比

将轮体、轴承和轴进行整体计算时，需在各配合面设置初始过盈量，分别查看各件的径向变形和剩余过盈量。

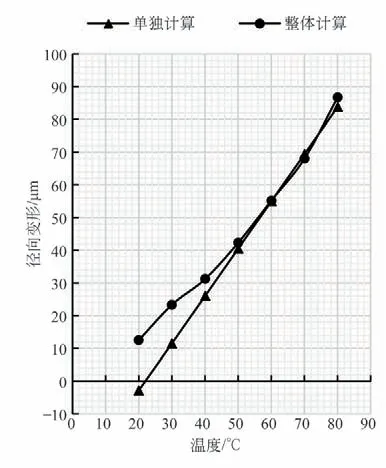
图6 轮体内孔径向变形对比

图7 轴外表面径向变形对比

由图6 和图7 可知，随着温度升高，轮体内孔和轴外表面的径向变形均逐渐增大，单独计算时变形量线性变化，整体计算时波动上升，但最终逐渐趋于一致，两种计算方式的结果差异不大。

图8 轴承内外圈径向变形对比

由图8 可知，轴承内外圈在不同计算条件的径向变形差异较大，单独计算时变形量线性变化，整体计算时波动上升，且内外圈整体计算中的径向变形比单独计算要大。

可知，过盈状态的内外圈的初始变形量均比自由状态下内外圈的初始变形量要大，这是由于整体计算时，轴承内外圈均处于过盈配合状态，受到较强的挤压作用，而轮体材料受热后发生膨胀变形，与轴承的过盈配合发生变化，部分区域变成过渡配合甚至间隙配合，导致轴承约束减少，径向变形量增加。

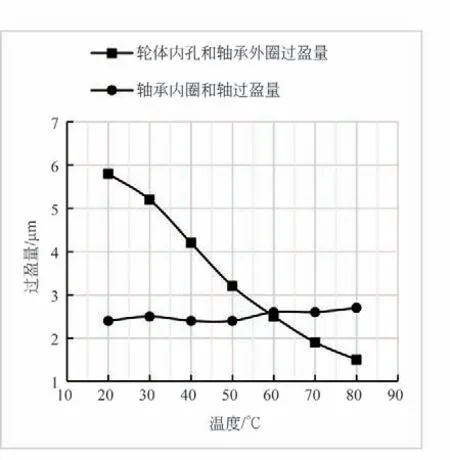
图9 升温过程中配合面过盈量变化

由图9 可知，轮体内孔变形较大，随着温度的升高，与轴承外圈的过盈量逐渐减少。如图10 所示，提取轴承外圈与轮体内孔的接触压力，可知大部分区域的接触压力很低，甚至为零，说明轴承外圈与轮体内孔的配合区域已经变成过渡配合甚至间隙配合。

图10 轴承外圈与轮体内孔接触压力

3 装配间隙的计算

由上述分析可知由于不同材料的线膨胀系数不同，受热时的变形量也不同，而尺寸的公差配合是以20℃为基准进行标注的，所以如果结合件材料的线胀系数不同，则需对各件之间的配合间隙（或过盈）进行修正计算，以选择比较正确的配合类别[1]。计算公式为

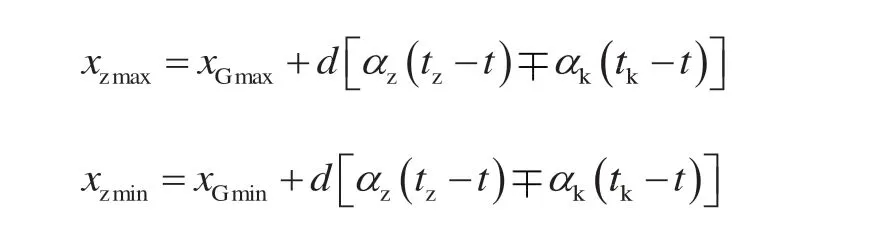
式中：xzmax、xzmin为装配间隙的最大值和最小值，tk、tz为孔和轴的工作温度，xGmax、xGmin为工作间隙的最大值与最小值，t 为装配时的环境温度，d 为公称直径，ak、az为孔和轴的线胀系数，负号用于温度提高导致孔的尺寸增大的情况，正号用于温度提高导致孔的尺寸缩小的情况。

4 结论

不同材料的线膨胀系数不同，导致受热时的变形量不同，从而影响配合精度。如果配合面会受到温度变化的影响，则应尽可能使有配合的部位使用同种材料，使配合面的变形尽量一致，避免对配合精度造成过大影响。若不可避免的使用不同材料进行配合，则在结构设计时需要考虑温度对公差配合的影响，并对配合间隙（过盈）进行合理的修正。