考虑非支持性评论的网络谣言传播模型

李 燕，陈巧萍

（上海海事大学经济管理学院，上海 201306）

0 引言

近年来，谣言传播问题备受关注，信息技术和社交软件的迅速发展，使得谣言传播的速度更快，范围更广，然而，谣言的蔓延有可能对人们的生活以及社会产生不容忽视的问题。例如：新冠肺炎疫情期间，深圳一男子编造“6 月17 日在辖区某地铁站发现确诊病例”的不实信息，并在网络中发酵，造成公众恐慌，因此，研究谣言的传播机制、探索有效的防控策略具有非常重要的现实意义。

基于网络谣言的传播与传染病的传播非常相似，传染病传播理论被广泛用于谣言传播研究之中。但是相对于传染病的传播，网络谣言传播受制于一些特定因素，例如：在线社交网络的复杂网络特征、社交应用程序的独特机制和人的社会行为属性等影响因素。据此，Zanette［1-2］和Moreno 等［3］分别研究并证实了小世界网络、无标度网络对谣言传播的影响；Xia等［4］在考虑谣言内容的吸引力和模糊性基础上，建立了改进的SEIR（Susceptible-Exposed-Infected-Removed）模型，发现减小模糊性能够抑制谣言传播，但传播阈值与吸引力无关；Liu等［5］研究了评论机制对在线社交信息传播的影响，结果表明较高的评论率更易于信息传播；Zhao 等［6］研究了遗忘机制和记忆机制对谣言传播的影响；马宇红等［7］研究了从众效应和权威效应对谣言传播的影响，证实了从众效应和权威效应能够显著扩大谣言传播范围；Jia 等［8］区分了谣言在社交网络上传播的两个渠道，即点对点传播和群体传播，并分析了两种渠道对谣言传播的影响；Ma 等［9］研究了积极和消极影响的两极社会强化，发现降低正强化因子或增加负强化因子可以有效抑制谣言传播；刘亚州等［10］考虑真实社交网络中节点的亲密度对谣言传播的影响，结果表明随着无标度网络中节点间平均亲密度增大，传播阈值会减小，谣言传播最终影响范围会变大；王丽婷等［11］分析了多传播源和导控措施对网络谣言传播的影响；Huo等［12］发现了个人的自我成长能力越强，谣言的范围越小，事件的不可识别度越大，谣言影响力越大；张菊平等［13］证实了当真实信息传播者的初始值不同时，谣言传播者的峰值也是不同的。综上所述，学者们已研究了多种不同因素对网络谣言传播的影响，研究成果为网络谣言传播机制以及防控策略的研究作出了重要的贡献；但现有的相关文献尚未研究非支持性评论对网络谣言传播影响，也未对其进行数学分析。在信息泛滥的网络时代，人们越来越依赖于通过用户评论来判断信息的可信度，即当谣言帖子下存在非支持性评论时，该条谣言帖子的可信度会受到影响，因此，非支持性评论对网络谣言传播的影响是不可忽略的。

基于上述原因，本文在考虑非支持性评论的影响和参考SIRaRu（Spreaders-Ignorants-Stifler1-Stifler2）谣言传播模型［14］的基础上，提出一个加入带有非支持性评论的谣言传播者的SIICR1R2（Susceptible-Infected-Infected with non-supportive comment-Removed1-Removed2）网络谣言传播模型并对其进行动力学分析。

1 SIICR1R2网络谣言传播模型的构建

本文根据网络谣言传播过程将用户分为五类：未知者S（不知道谣言的用户），谣言传播者I（相信并传播谣言的用户，并且该用户的谣言帖子下不存在非支持性评论），带有非支持性评论的谣言传播者IC（相信并传播谣言的用户，但该用户的谣言帖子下存在非支持性评论），第一种免疫者R1（相信谣言但不传播谣言的用户）和第二种免疫者R2（不相信谣言的用户）。

为了SIICR1R2网络谣言传播模型能够较好地描述非支持性评论对网络谣言传播的影响，根据在线社交网络平台中非支持性评论的实际情况，作出以下合理规定：

1）本文所考虑的非支持性评论主要是指反驳性评论和怀疑性评论。群众对谣言的批判和怀疑会影响个体对谣言的判断，从而抑制谣言的传播［15］。Zan 等［16］发现了反击机制的存在可以降低谣言传播速度和最终影响范围。夏志杰等［17］发现了质疑机制抑制谣言传播。

2）非支持性评论不仅包括反驳性评论，还包括怀疑性评论，因此存在该评论的说服力不强或者支持性评论的影响力远大于非支持性评论的影响力，而导致用户在看到非支持性评论后仍然相信谣言的情况。

3）事实上，存在少数用户会删除与自己意见相反的评论，或者支持性评论的数量远大于非支持性评论的数量，导致他人看不到非支持性评论的情况。

图1 示意的是SIICR1R2网络谣言模型的传播过程，具体传播规则定义如下：

1）用户以恒定的移入率A进入在线社交网络并且全部为未知者，而且每个类别的用户以相同移出率μ移出在线社交网络。

2）未知者以概率θ与谣言传播者接触，接触之后：若未知者相信并传播谣言，则以概率α1转变为谣言传播者；若未知者相信但不传播谣言，则以概率γ1转变为第一种免疫者，其中，α1+γ1称为谣言的相信率；若未知者不相信谣言，则以概率1-α1-γ1转变为第二种免疫者。

3）未知者以概率θ与带有非支持性评论的谣言传播者接触，接触之后：若未知者相信并传播谣言，则以概率α2转变为谣言传播者；若未知者相信但不传播谣言，则以概率γ2转变为第一种免疫者，其中，α2+γ2称为带有非支持性评论的谣言的相信率；若未知者不相信谣言，则以概率1-α2-γ2转变为第二种免疫者，由于非支持性评论的抑制作用，α1+γ1≥α2+γ2。

4）当谣言传播者与带有非支持性评论的谣言传播者接触时，若谣言传播者被非支持性评论说服，则谣言传播者以概率ε转变为第一种免疫者。

5）谣言传播者经过一段时间后，由于遗忘或者兴趣衰减，不再传播谣言，即谣言传播者会以概率λ转变为第一种免疫者；谣言传播者可能接收到他人的非支持性评论，即谣言传播者会以概率β转变为带有非支持性评论的谣言传播者，其中，β称非支持性评论率。

6）带有非支持性评论的谣言传播者可能因为遗忘或兴趣衰减，也可能因为非支持性评论，不再传播谣言，即带有非支持性评论的谣言传播者以概率δ转变为第一种免疫者。

7）带有非支持性评论的谣言传播者可能因为删除与自己观点相反的评论，还可能因为该谣言帖子下的支持性评论的数量远大于非支持性评论的数量，导致他人看不到该谣言帖子下的非支持性评论，即带有非支持性评论的谣言传播者以概率σ恢复为谣言传播者，其中σ称为恢复率。

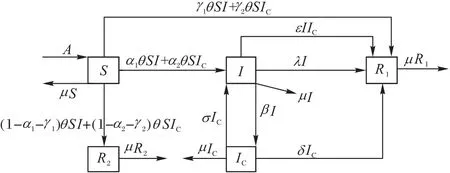
图1 SIICR1R2网络谣言传播模型Fig.1 SIICR1R2internet rumor propagation model

用S(t)、I(t)、IC(t)、R1(t)、R2(t)分别表示未知者、谣言传播者、带有非支持性评论的谣言传播者、第一种免疫者和第二种免疫者在t时刻的数量。用U(t)表示用户总数量，即U(t)=S(t)+I(t)+IC(t)+R1(t)+R2(t)，kˉ表示网络平均度。根据以上传播规则，建立SIICR1R2网络谣言传播模型的动力学方程如下：

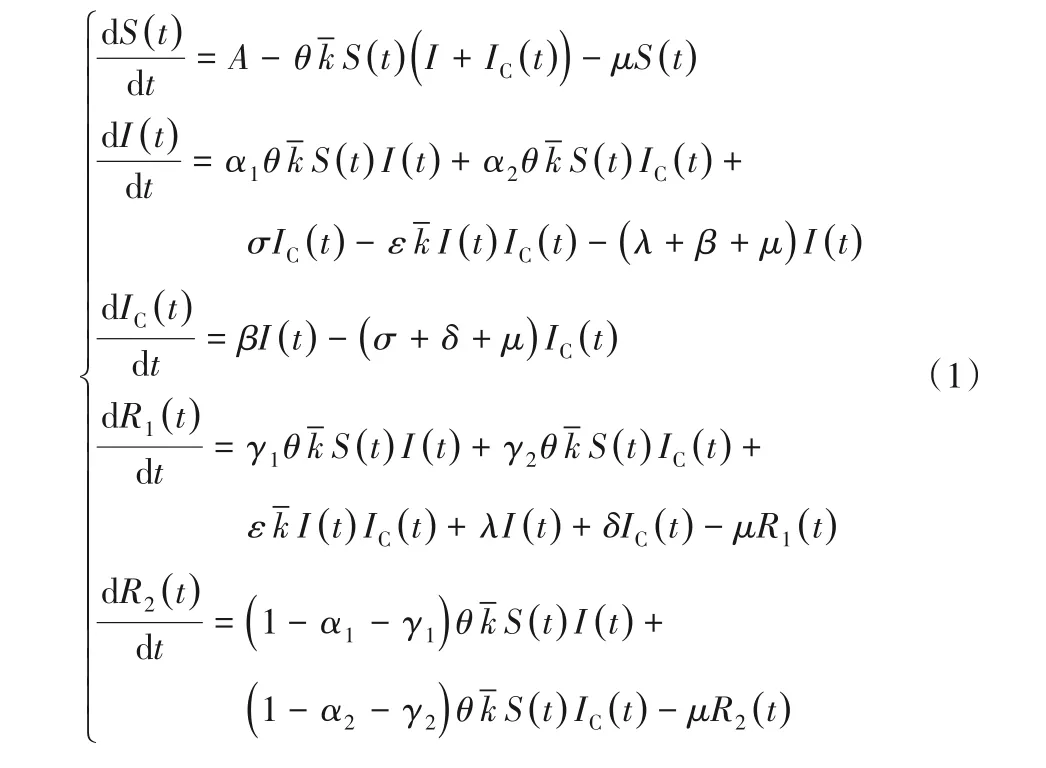
2 SIICR1R2网络谣言传播模型的稳态分析

2.1 基本再生数求解

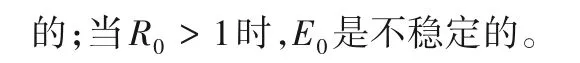
2.2 无谣言平衡点的全局稳定性分析

2.3 谣言传播平衡点求解

2.4 谣言传播平衡点的局部稳定性分析

2.5 谣言传播平衡点的全局稳定性分析

3 数值仿真与分析

为了验证上述理论结果和分析参数对网络谣言传播的影响，本文的仿真实验使用Matlab软件，以U0=106=10的均质网络作为底层网络，根据参考文献［13］设定参数值，并使用Runge-Kutta（龙格库塔法）方法求解式（1）。

未知者S和谣言传播者I的初始密度分别设置为0.8、0.2。当参数取值为α1=0.3，α2=0.05，β=0.3，A=0.2，μ=0.2，θ=0.1，ε=0.15，λ=0.01，σ=0.01，δ=0.2，γ1=0.1，γ2=0.05=10 时，R0=0.67 ＜1，则E0是渐进稳定的，仿真结果与理论结果相符合（见图2），本文所有图片均以用户密度变化表示用户数量的变化。

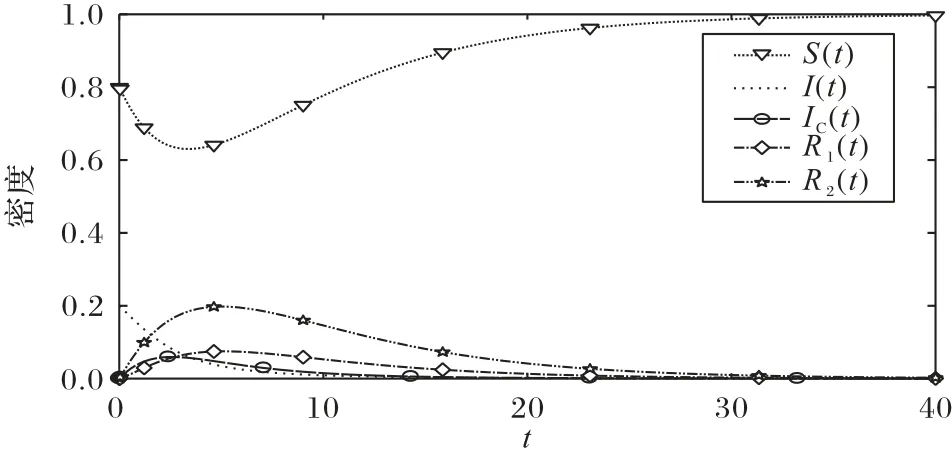
图2 无谣言平衡点E0的稳定性Fig.2 Stability of rumor-free equilibrium E0

未知者S和谣言传播者I的初始密度分别设置为0.8、0.2。当参数取值为α1=0.3，α2=0.05，β=0.3，A=0.2，μ=0.2，θ=0.4，ε=0.15，λ=0.01，σ=0.01，δ=0.2，γ1=0.1，γ2=0.05=10 时，R0=2.68 ＞1，则E*是渐进稳定的，仿真结果与理论结果相符合（见图3）。

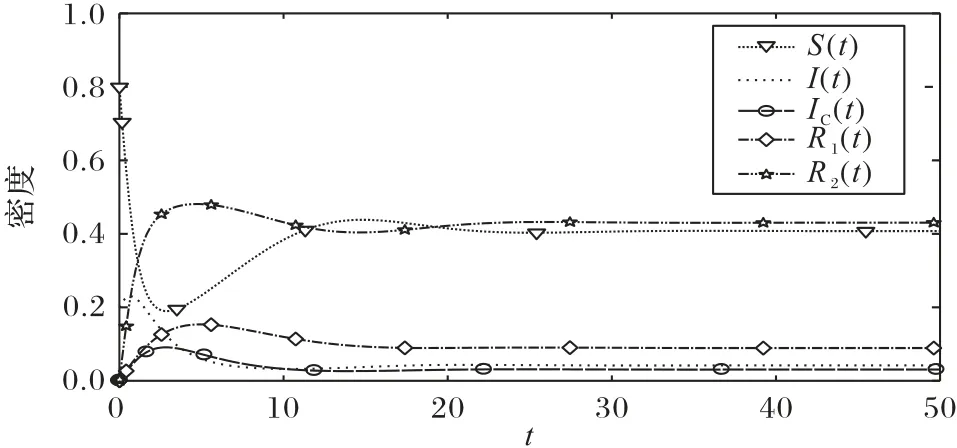
图3 谣言传播平衡点E*的稳定性Fig.3 Stability of rumor propagation equilibrium E*

接下来仿真分析参数对网络谣言传播的影响，若无特别说明，将未知者S和谣言传播者I的初始密度分别设置为0.999 999、10-6，参数设置为α1=0.3，α2=0.05，β=0.5，A=10-6，μ=10-6，θ=0.4，ε=0.15，λ=0.01，σ=0.01，δ=0.2，γ1=0.2，γ2=0.1=10。

为了研究非支持性评论率β和恢复率σ对网络谣言传播的影响，定义网络谣言传播过程中总谣言传播者数量的峰值即ZMAX=(I+IC)MAX，总谣言传播者数量达到峰值的时间TMAX以及网络谣言传播稳定后，最终受谣言影响的范围R1(∞)三个指标来衡量这些参数对网络谣言传播的影响。

图4 表示的是恢复率σ=0.1，0.3，0.5，0.7 的情况下，总谣言传播者数量的峰值ZMAX，达到峰值的时间TMAX和网络谣言最终影响范围R1(∞)随着非支持性评论率β的变化情况。从图4可以看出，非支持性评论率β越大，ZMAX的值越小，TMAX的值越大，R1(∞)的值越小。从图4（b）和图4（c）还可以看出，当恢复率σ逐渐减小时，TMAX的值随着非支持性评论率β增大而增大的趋势越明显，R1(∞)的值随着非支持性评论率β增大而减小的趋势也越明显。这可以解释为当恢复率σ较小，非支持性评论对网络谣言传播的抑制作用较大，因此变化趋势越明显。

图5 表示的是非支持性评论率β=0.1，0.3，0.5，0.7 的情况下，总谣言传播者数量的峰值ZMAX，达到峰值的时间TMAX和网络谣言最终影响范围R1(∞)随着恢复率σ的变化情况。从图5可以看出，当非支持性评论率β较大时，恢复率σ越大，ZMAX越大，R1(∞)越大，TMAX越小，且这些变化趋势更明显。当非支持性评论率β较小时，恢复率σ的变化会引起ZMAX、R1(∞)和TMAX产生波动，但是总体变化趋势不明显。这主要因为恢复率是作用于带有非支持性评论的谣言传播者，所以当带有非支持性评论的谣言传播者的数量处于一个小的值时，恢复率对其的影响也会很小。

综上所述，非支持性评论率β和恢复率σ均对网络谣言传播具有显著影响。此外，将恢复率σ保持在较低值的前提下，提高非支持性评论率β，非支持性评论对网络谣言的抑制效果会更好。

分析非支持性评论的说服力对网络谣言传播的影响。考虑到非支持性评论的说服力主要在五个状态转变过程中体现，其中包括未知者遇到带有非支持性评论的谣言传播者时，未知者转变为谣言传播者、第一种免疫者和第二种免疫者三种状态之一；谣言传播者在遇到带有非支持性评论的谣言传播者时，可能会转变为第一种免疫者；带有非支持性评论的谣言传播者可能因为非支持性评论转变为第一种免疫者。这五个转变过程涉及到的概率有α2、γ2、ε和δ。因此本文主要通过概率α2、γ2、ε和δ来考察非支持性评论的说服力对网络谣言传播的影响。

图6表示的是概率α2，γ2，ε和δ不同的三种网络谣言传播模型中总谣言传播者数量Z(t)和谣言影响范围R1(t)随时间的变化情况。从图6 可以看出：非支持性评论的说服力越大，总谣言传播者数量的峰值越小，网络谣言的最终影响范围越小，但对总谣言传播者数量达到峰值的时间影响不大。因此，结论为非支持性评论能够降低谣言帖子的可信度，并且非支持性评论的说服力越大，谣言帖子的可信度就越小，从而抑制网络谣言的传播。

分析传播率对网络谣言传播的影响。从网络谣言传播规则可知，传播率的变化主要是通过α1、α2、γ1和γ2这四个概率变化来体现的，因此通过α1、α2、γ1和γ2这四个概率来考察传播率对网络谣言传播的影响。本文设计了相信率(α1+γ1，α2+γ2)不变，概率α1、α2、γ1和γ2不同的三种网络谣言传播模型，并将不同模型中Z(t)和R1(t)的变化情况进行比较，如图7所示。

图4 不同恢复率σ下，ZMAX、TMAX和R1（∞）随着非支持性评论率β的变化图Fig.4 ZMAX，TMAXand R1（∞）changing with non-supportive comment probability β under different recovery probability σ

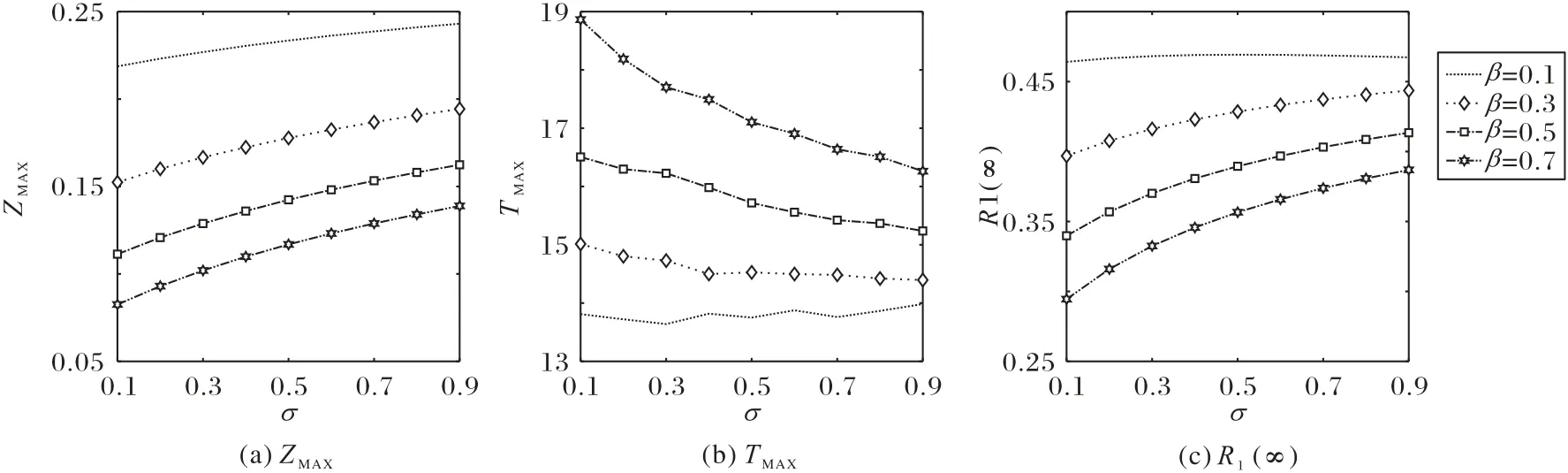
图5 不同非支持性评论率β下，ZMAX、TMAX和R1（∞）随着恢复率σ的变化图Fig.5 ZMAX，TMAXand R1（∞）changing with recovery probability σ under different non-supportive comment probability β

图6 不同α2、γ2、ε和δ下，Z（t）和R1（t）随时间的变化图Fig.6 Z（t）and R1（t）changing with time under different α2，γ2，ε and δ

图7 不同α1、γ1、α2和γ2下，Z（t）和R1（t）随时间的变化图Fig.7 Z（t）and R1（t）changing with time under different α1，γ1，α2and γ2

从图7 可知，随着传播率的增大，总谣言传播者数量的峰值越大，达到峰值的时间越快，网络谣言传播速度越快，最终影响范围也越大。这说明在相信率不变的情况下，未知者相信谣言后，越倾向于传播，那么其转变为谣言传播的概率就越大，从而导致谣言传播者的数量越大，网络谣言传播的范围越广。

以上分析都是基于均质网络进行的，实际上，在线社交网络存在小世界、无标度等特性，因此，下面分别以BA（Barabási-Albert）无标度网络和WS（Watts-Strogatz）小世界网络为底层网络进行仿真，分析不同网络拓扑结构和不同网络拓扑结构下参数β对网络谣言传播的影响。WS 小世界网络的节点数为1 000，网络平均度=10；BA 无标度网络的节点数为1 000，网络平均度=10；参数值设置为α1=0.3，α2=0.2，A=10-6，μ=10-6，θ=0.4，ε=0.1，λ=0.01，σ=0.01，δ=0.11，γ1=0.2，γ2=0.1。每次仿真过程都是随机选择一个用户作为初始谣言传播者，仿真结果为100次独立运行的平均。

从图8～9 可知：在BA 无标度网络和WS 小世界网络中，β值的变化虽然对总谣言传播者数量达到峰值所需时间的影响不显著，但是总谣言传播者数量Z(t)和谣言最终影响范围R1(t)均随着β增加而减小，由此可得，非支持性评论对网络谣言传播具有抑制效果；WS小世界网络中谣言最终影响范围稍大于BA 无标度网络，但是WS 小世界网络中总谣言传播者数量达到峰值所需时间明显大于BA无标度网络。

根据以上分析结果，提出以下谣言防控策略：

1）可以通过教育、宣传等途径来提高公众识别谣言的能力和思辨能力，这不仅能提高非支持性评论率，还能使他们所发表的非支持性评论具有更高的说服力。

2）可以通过一些激励措施，即鼓励公众对其能够识别或怀疑的谣言帖子通过评论渠道提出自己反对或怀疑的看法，也可以通过外部干预，对谣言帖子进行标识，提高非支持性评论率，让公众能够更容易识别出谣言。

3）可以通过采取宣传、惩罚等措施来提高公众的责任意识，谨慎发表言论，避免公众因为自己的不当言论而遭受惩罚。

4）可以通过媒体报道进行辟谣，扩大辟谣信息的覆盖范围，进而减少谣言帖子下的支持性评论的数量，提高谣言帖子下非支持性评论的数量。

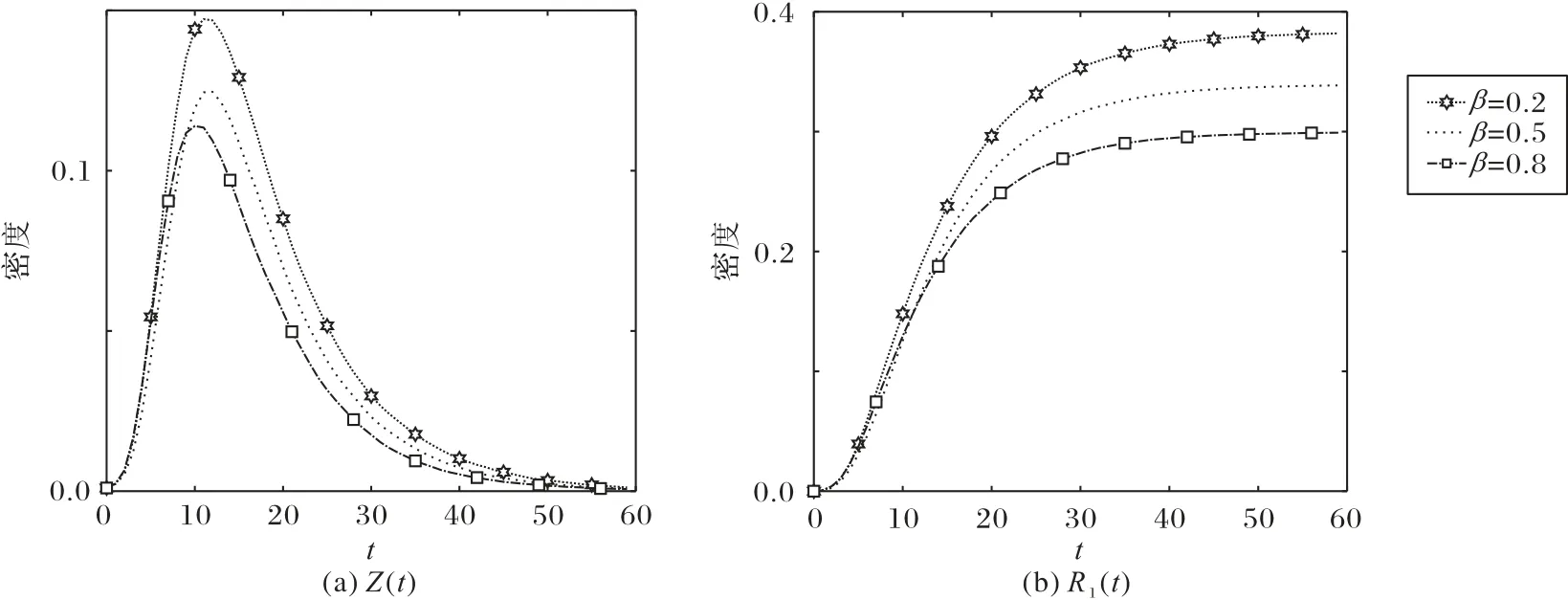
图8 不同β值下，Z（t）和R1（t）在BA无标度网络中随时间的变化图Fig.8 Z（t）and R1（t）changing with time in BA scale-free network under different β

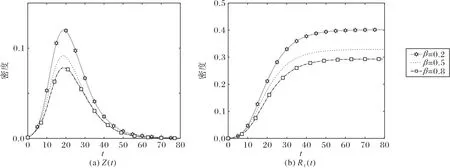
图9 不同β值下，Z（t）和R1（t）在WS小世界网络中随时间的变化图Fig.9 Z（t）and R1（t）changing with time in WS small-world network under different β

4 结语

本文重点研究了非支持性评论对网络谣言传播的影响，建立一个引入带非支持性评论的谣言传播者的SIICR1R2网络谣言传播模型，并对其进行稳态分析和数值仿真分析。所得结论：在将恢复率σ保持较低值的前提下，提高非支持性评论率β，非支持性评论率对网络谣言的抑制效果更佳；非支持性评论的说服力越强，网络谣言的影响范围越小，但对网络谣言传播速度影响不大；传播率越大，网络谣言传播速度越快，影响范围越大。此外，基于WS 小世界网络和BA 无标度网络的模型仿真结果再次证实非支持性评论对网络谣言传播具有抑制作用。该仿真结果也表明：与WS 小世界网络相比，网络谣言在BA 无标度网络中的影响范围略小，但网络谣言在BA 无标度网络中的传播速度更快。根据以上结论，可以采取鼓励、宣传教育和惩罚等防控措施来提高非支持性评论率和说服力，降低传播率和恢复率，从而抑制网络谣言传播。

本文模型重点研究了非支持性评论对网络谣言传播的影响。在现实生活中，谣言帖子下不仅存在非支持性评论，还存在支持性评论，因此研究非支持性和支持性评论的网络谣言传播模型将是今后研究的一个方向。