TDCS大规模分区多址通信方法

宋耀辉 黄仰超 高维廷 胡 航 谷奕龙

(空军工程大学信息与导航学院, 陕西西安 710077)

1 引言

随着各类通信设备的增多,电磁频谱环境日益复杂,传统的频谱分配方案越来越难以满足当前的通信需求,于是基于频谱感知和见缝插针的认知无线电(Cognitive Radio, CR)思想被提出,并被认为是提高频谱利用率,解决频谱拥堵问题的重要方案[1-2]。在CR领域的诸多技术中,变换域通信系统(Transform Domain Communication System, TDCS)是不可忽视的一部分,采用CR思想和扩频通信思想融合,在复杂电磁环境下具有很强的适应力。TDCS最早应用在军事通信中,重在解决小的作战单位深入敌军内部时,面对激烈的电磁对抗,如何实现我军内部隐蔽可靠通信的问题[3- 4]。近年来,TDCS以其多用户通信的优势[5],在民用通信中得到了越来越多的重视,如:认知无线电网络(Cognitive Radio Networks, CRNs),5G无线通信系统,物联网(internet of things, IoT)等[6- 8,13]。

多用户通信是TDCS研究领域的热点问题,由于频谱状态的不确定性,在为各个用户分配不同基函数通信时,难以做到基函数间的严格正交[7],因此多用户干扰成为影响通信质量和阻碍TDCS用户数提高的主要因素。文献[9]基于传统m序列生成基函数,研究了TDCS多址通信时的互相关值及对误码率的影响,为后续研究提供参考;文献[10]在基函数生成时嵌入PSK调制信号,改善了信噪比,从而提升多用户之间的互相关性能;文献[11]使用扩频序列对伪随机相位编码,降低了TDCS多址通信的实现难度,且其多用户性能和传统方案相当;文献[12]针对TDCS提出一种低自相关旁瓣的序列生成算法,相对传统方案,序列自相关性和互相关性都有所改善;在多址通信时,上述方法相对传统方法在性能上都有所提高,但无法胜任大规模TDCS多址通信。文献[13]采用分集思想,将整个可用频段分为若干区域,为功率大小相近的用户分配相同频段通信,降低了远近效应和多址干扰的影响,但是各用户并未对整个频谱充分利用;文献[14]使用互相关性为0的完美序列对基函数频谱扩展,使各用户占据不同区域,从而避免了用户间干扰,但是生成完美序列要求较高[15],且各个区域未得到充分利用。

在以上研究基础上,本文提出一种面向大规模用户的TDCS多址通信方法。由于基函数难以做到严格正交,因此考虑用户分区策略,使得区间用户的干扰降低,从而提高用户数。分区函数的自相关旁瓣越小,区间干扰就越小,因此在以基函数作为分区函数的基础上,引入CAN算法对其进一步优化,提高自相关性能。在此基础上,对该方法的误码率和频谱效率等性能进行分析,提出高斯信道下的分区向量最优长度的计算方法。最后进行误码率和频谱效率仿真,验证所提方法的性能。

2 TDCS原理

TDCS是一种隐蔽和保密性强,具有多址能力的通信方法。经过幅度谱生成、伪随机相位映射和功率控制等形成基函数,并对基函数调制。基函数具有伪随机性,只有接收端产生与发送端相同的基函数时才能解调出信号。并且基函数之间是近似正交的,通信时各个用户生成自己独有的基函数[5]。

幅度谱生成时,以固定间隔对整个频段N点采样,采样值与预设门限相比,高于门限值时标记为1,低于门限值时标记为0。其中,标记为1的频段表示可用频段;标记为0的频段表示不可用频段。这样,便得到长度为N的幅度谱向量A。

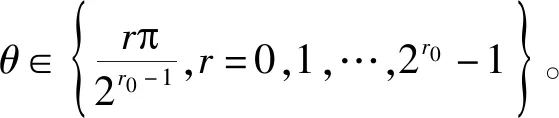
令幅度谱向量与伪随机相位向量逐位相乘,并进行反傅里叶变换,得到长度为N的基函数b,如式(1)

(1)

其中

(2)

若基函数自相关峰值为1,则旁瓣接近于0。因此,通常采取ccsk调制方式,接收端使用与发送端相同的基函数,对其取共轭与接收信号卷积,寻找峰值位置,解调出数据信息,如式(3)

d=max|b⊗r|

(3)

式中,max|·|为寻找峰值位置运算,r为接收信号。

对于M-ccsk,其误码率与正交调制近似[16],可表示为

(4)

其中

H(x)=[1-e-x]M-1

(5)

I0(·)为修正的第一类零阶Bessel函数,q为信号能量与噪声功率谱密度之比。

存在多址干扰情况下,该信噪比考虑基函数的相关函数。当用户数为U时,得到基函数矩阵B=[b1,b2,…,bU]。其中用户i与用户j的相关函数为:

(6)

式中,n=0,1,…,N-1,⊗为循环卷积运算。

则信噪比可表示为

(7)

式中,k为调制信号携带的数据比特数,且k=log2M。

由上式可知,在有用信号自相关函数确定情况下,减少其他用户数量或减小用户间基函数的互相关值可提高信噪比,改善系统的误码率性能。下一节将提出一种避免多址干扰的方法,对信号频谱扩展并分成相互干扰很小的区域,使各用户在区域内进行M-ccsk调制。控制每个区域的用户数量,实现一定误码率条件下的用户数扩充。

3 大规模多址通信方法

大规模分区多址是对传统基函数进行ccsk调制后,利用分区函数对其进行频谱扩展与分区,成为包含用户数据的基函数xi,对xi功率控制并发送。接收端对应产生与发送端相同且位于同一分区的基函数yi,与接收信号相关卷积,利用ccsk解调出数据信息,如图1。

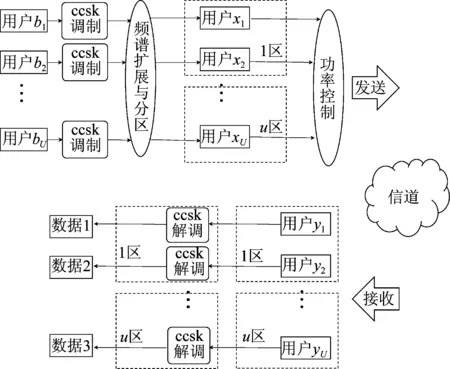
图1 TDCS分区多址通信原理图Fig.1 Schematic diagram of TDCS partition multiple access communication

假设c为一组长度为L的向量,且自相关性较好,即

(8)

式中,ε为变量,且趋近于0。该向量将用于用户分区,减少不同分区间用户的相互干扰。该向量的生成方法在第3节详细介绍。

结合(1)、(8),将向量c与基函数bKronecker相乘,得到一组新的基函数x,且其长度为N×L,如式(9)

x(n)=[c1bT,c2bT,…,cLbT]T

(9)

其中,n=0,1,…,NL-1,ci为常数。

为方便讨论,不妨设用户数U为序列c长度的整数倍,即

u=U/L,u∈N+

(10)

则基函数矩阵B被平均分为u个分区

(11)

其中,i=1,2,…,u,[bi]N×1为用户i的基函数。

将序列c与各分区基函数移位相乘,得到新的基函数矩阵[X]LN×U

(12)

其中,i=1,2,…,u,xj为分区后用户j的基函数,由向量c的i位循环左移与bj进行Kronecker相乘得到的,且bj∈Bi,即

(13)

此时,用户i与其他用户相关函数为:

(14)

式中,xj1与xi处于相同分区,且j1≠i;xj2与xi处于不同分区。则用户间的多址干扰被分为分区内干扰和分区间干扰。

对于分区内用户:

(15)

对于分区间用户:

(16)

由(15)～(16)可知,在基函数互相关性相差不大情况下,由于向量c有良好自相关性,分区内干扰影响较大,而分区间干扰影响较小。下节介绍一种自相关旁瓣值较小的分区函数生成方法。

4 分区向量生成方法

根据第3节多址干扰的分析可知,除了要求分区向量具有较小的自相关旁瓣以外,由于总用户的分区数不确定,因此要求分区序列的长度能灵活调整。文献[17]提出一种CAN算法,能基于伪随机序列快速产生自相关性优良的单模向量,且向量长度由伪随机序列长度决定,最高可达到106。因此,考虑使用CAN算法生成分区向量。该算法要求使用自相关性较好的单模序列进行初始化,在此考虑使用长度为L的基函数。具体算法如下:

步骤1根据式(1),生成长度为L的基函数b0,作为初始分区向量c;

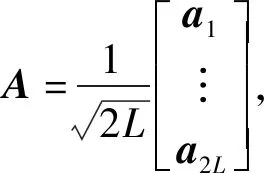
步骤3在向量c末尾添加L个0,拓展为2L×1的列向量:z=[c(1)…c(L) 0…0]T;

步骤4使f=A*×z,并对f中各元素取角度:φp=arg[f(p)],p=1,…,2L;然后将其进行归一化处理,生成相角向量ν=[ejφ1,…,ejφ2L]T;

步骤5使g=A×ν,同样对结果取相角,做归一化处理,得向量C=[ejarg[g(1)],…,ejarg[g(2L)]]T,取前L位即为所求分区向量c;

步骤6重复步骤3到步骤5,直到||cn-cn-1||<σ。其中n为迭代次数;σ为预设常数,通常很小但不为0。

5 性能分析

第3节介绍了TDCS大规模多址分区原理,但在使用时需要考虑误码率和频谱效率等问题,下面以高斯信道为例,对用户实行各区的均匀分配,对上述两个指标进行研究。

5.1 误码率

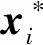
在高斯信道条件下,接收信号为:

(17)

式中,U为总用户数,hi, j为用户j对用户i的路径增益,ni为高斯白噪声。

由文献[14],该信道条件下r与xi的相关函数为

(18)

式中,φi, j为xi与xj的相关函数。

结合(15)～(16),将(18)进一步分解

(19)

式中,j1为分区内用户,j2为分区外用户。

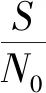
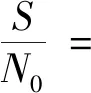
(20)

式中,i=1,…,U,||·||为求向量模值运算,bi为用户i的原始基函数。

将(20)结果带入式(4)即为分区方案的误码率。

在3 dB信道噪声条件下,误码率与用户数的函数图像如图2。

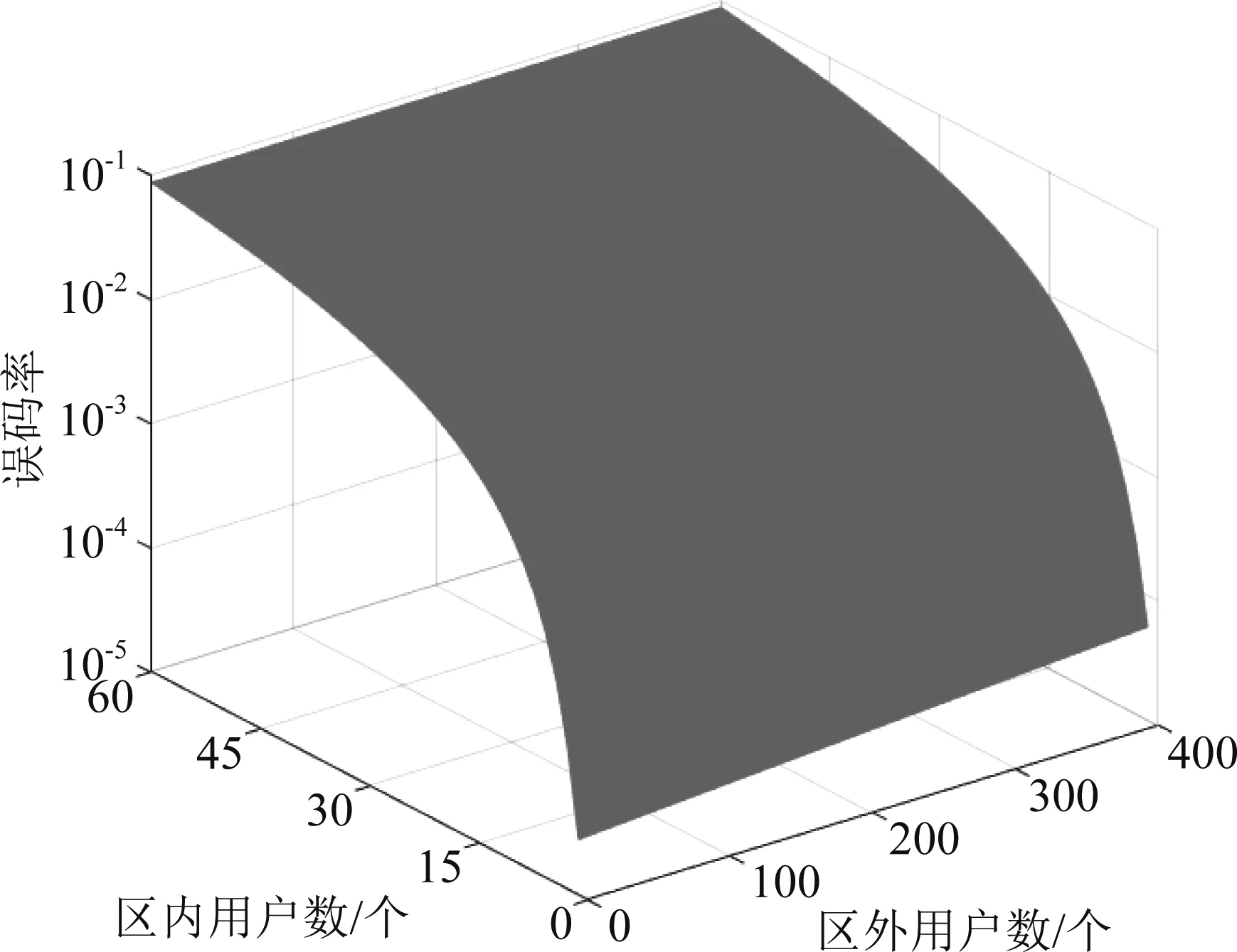
图2 分区多址用户数与误码率关系Fig.2 The relationship between the number of users of partition multiple access and bit error rate

由图可知,误码率随区间内用户数成对数上升,而随区间外用户数成一条斜率较小的直线上升。这也说明了,区间内用户数对误码率曲线的影响起主要作用,而由于分区函数自相关旁瓣不为0,分区外用户数对误码率也产生一定影响。

5.2 频谱效率

文献[14]推导出,各分区用户数为1时,系统频谱效率为

(21)

式中,β为幅度谱中标记为1的点个数所占向量总长度的比;Mmax为最大ccsk移位距离。在本文中,每个分区长度都为N,各用户在其分区内可选择不大于分区长度的移位距离,因此,最大ccsk移位距离Mmax=N。

由(21)可知,在用户数和基函数长度确定条件下,系统频谱效率与分区向量长度成反比关系,因此,最优分区向量长度要尽可能小以提高频谱效率。同时,随着分区数的减少,使得每个分区内的用户数增加,多址干扰增加迅速,影响误码率。综上所述,兼顾频谱效率和误码率等方面因素,分区向量存在最优长度。

假设U个用户被均匀分配到各个分区,在一定误码率条件下,每个分区最多能容纳a个区内用户,或b个区外用户。不妨令每个分区分配x个用户,列出一元不等式组

(22)

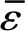
解不等式(22),L取最小整数

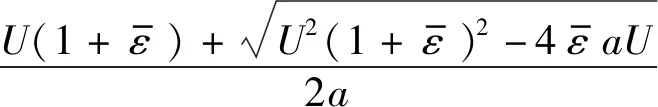
(23)

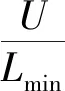
由此,用户被均匀分配到Lmin个分区中,可在所控误码率范围内,最大程度提高频谱效率。

6 仿真分析

仿真1多用户下的系统误码率仿真

本仿真验证系统误码率随用户数的变化。幅度谱标记点假设全为1,利用matlab随机函数生成伪随机相位,构成原始基函数b,其长度N=1024。将用户均匀分配到各分区,分区向量动态变化,长度L根据式(23)计算。信道采用-3 dB高斯白噪声信道,误码率水平设置为10-5。用户数设置1到400,分别产生10000组数据进行1024-ccsk调制。对比分析未分区多址通信方法、大规模分区多址通信方法和文献[7]中的单用户单分区多址通信方法的误码率性能,仿真结果如图3所示。

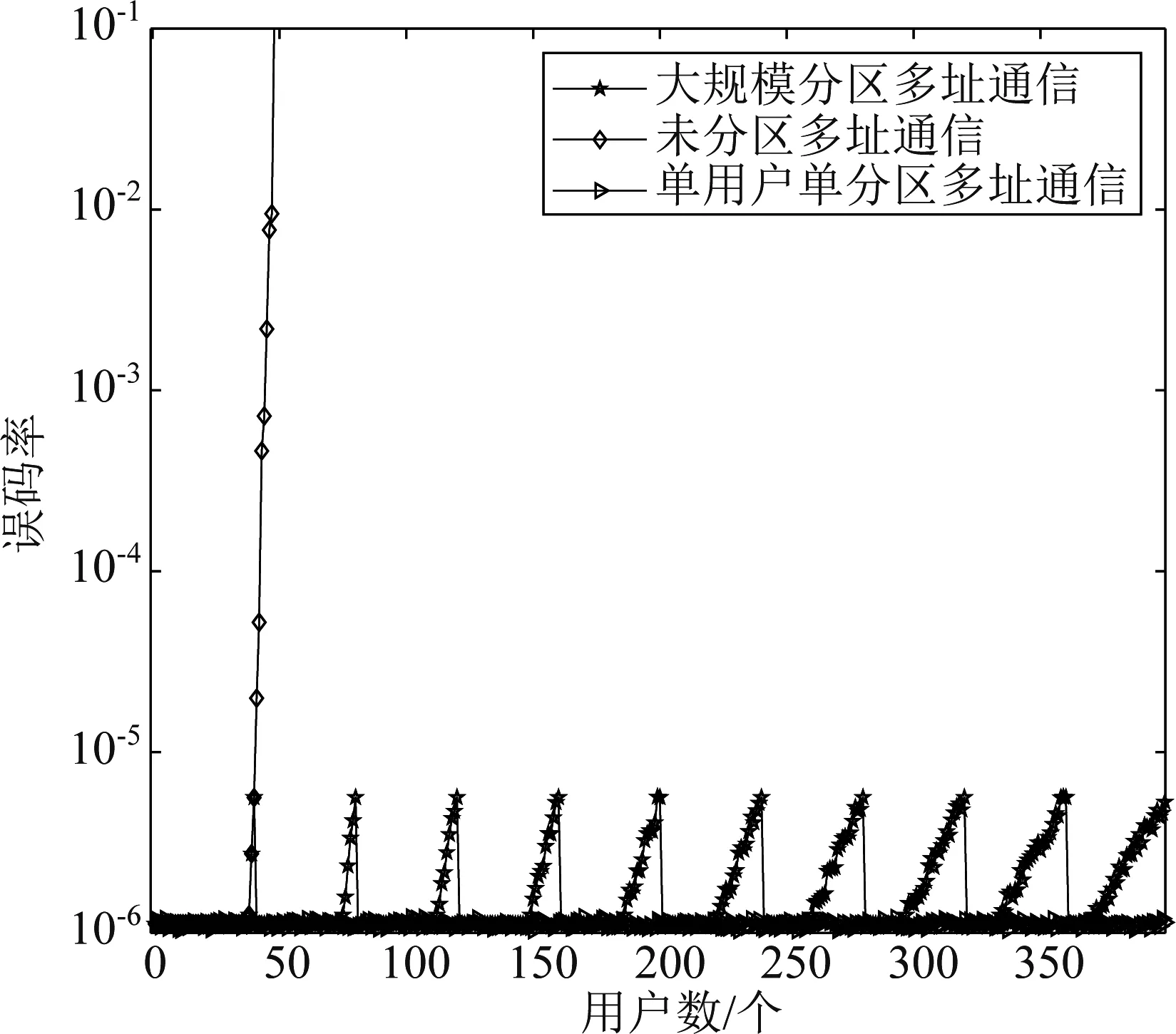
图3 不同用户数下的误码率Fig.3 Bit error rate for different users

由图可知,未分区方法和大规模分区方法的误码率曲线随着用户数的增多而发生变化;而文献[7]中的单用户单分区方法的误码率几乎不受用户数变化的影响,并始终保持在最低水平。这是由于单用户单分区方法使用完美序列进行分区,不同区块之间严格正交,而每个区块内只分配一个用户,因此误码率不受多址干扰的影响,只受信道噪声的影响。

对比未分区方法和大规模分区方法,当用户数达到45左右时,两种方法的误码率都升高到接近10-5。此时,两种方法的误码率曲线开始出现分离。未分区方法误码率随着用户数增加而持续迅速增大,并在用户数为75左右时,达到0.1,因此对于误码率不具备调节能力。大规模分区方法误码率则骤然降低到10-6,出现第一个不连续点,并随着用户数继续增多,误码率曲线出现类似循环的波动,且这样的波动逐渐趋于稳定。这是由于分区内用户数达到饱和时,分区数增加,使得用户在各个分区重新分配,每个分区内的用户数减少,多址干扰降低,误码率下降;另一方面,由于每个分区的容量有限,而随着用户基数的不断增大,使得增加分区对减小误码率的空余度降低,因此其误码率曲线将逐渐趋于稳定。

仿真2频谱效率仿真

本仿真验证所提方法的频谱效率。基函数生成条件和仿真1相同,分区向量长度L随用户数动态选择。高斯信道中,信噪比设置为-3 dB,误码率水平设置为10-5。用户数设置为1到2000,对比分析单用户单分区方法和大规模分区方法的频谱效率,如图4。

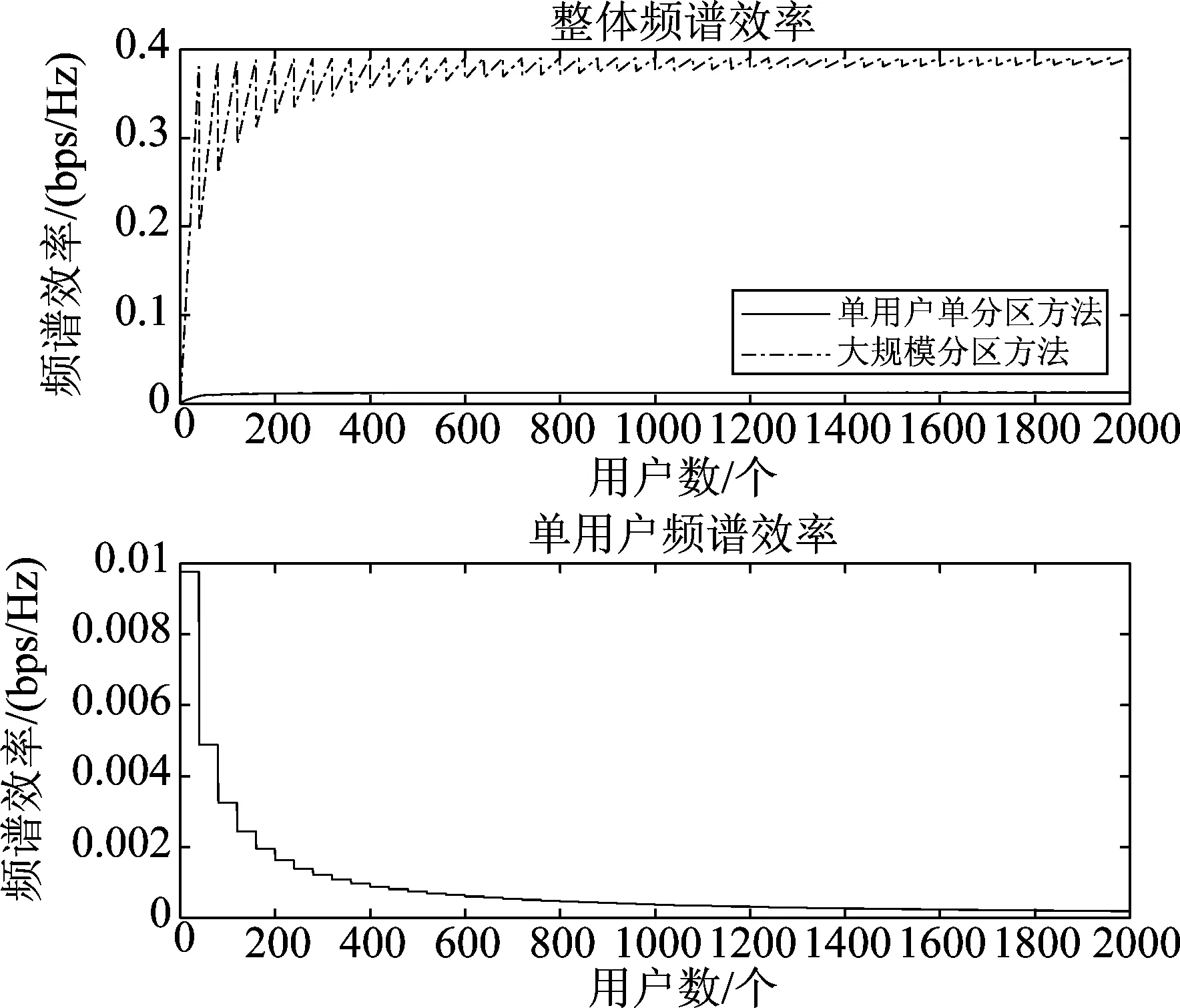
图4 频谱效率与用户数Fig.4 Spectrum efficiency for different users

对比两种方法的整体频谱效率可以看出,大规模分区方法的整体频谱效率随用户数增加而波动上升,最终在接近0.4 bps/Hz时趋于稳定,且其整体频谱效率约为单用户单分区方法频谱效率的30倍,因此大规模分区方法对频谱的利用更加充分。相对的,由大规模分区方法的单个用户频谱效率曲线可以看出,对于每个用户,其频谱效率随着总用户数的增加而呈现波动式下降趋势。由此可以看出,分区数增多在扩充用户数的同时,增加了信息的编码长度,即增加了每个用户的编码负担。

7 结论

本文提出了一种基于分区函数的TDCS大规模多用户通信方法。与传统TDCS多址方法相比,该方法通过增加信息冗余,降低误码率,即以单用户的频谱效率为代价换取总用户数的提高。在高斯信道下,采取用户在各个分区中均匀分配的策略,并给出最优分区向量长度的计算方法,保证系统整体性能最优。仿真结果表明,所提方法在-3 dB高斯信道下,用户数比传统的不分区方法提高数十倍,且误码率能稳定控制在较低水平;总体频谱效率较高,并随着用户数增加而趋于稳定。因此,该方法能极大程度满足大规模TDCS多址需求。