起伏目标相干检测性能分析

王 杰 刘 剑 黄子芹 肖 楠

(空军工程大学信息与导航学院, 陕西西安 710077)

1 引言

雷达的目标检测主要解决的是目标有无的判决问题,这始终是衡量雷达性能高低的最重要因素之一[1]。随着隐身技术的日趋成熟,飞机、导弹等目标的雷达横截面(Radar Cross Section, RCS)减小了一到两个数量级。目标RCS变小使得目标回波能量减小,雷达的目标检测性能随之大为降低[2]。现代战争中,隐身飞机外、巡航导弹和无人机等高速机动的低可探测目标(Low observable targets),除RCS极低外,其RCS也是起伏的,这就对雷达的检测性能提出了严峻的挑战[3]。

要提高雷达对于隐身飞机等目标的检测性能,本质上就是要在极低的信噪比(Signal to Noise Ratio, SNR)的条件下,尽可能提高雷达目标回波能量[4]。针对隐身飞机等目标RCS极低的情况,通常采用脉冲积累的方法。脉冲积累又分为相参积累和非相参积累,非相参积累未利用回波信号的相位信息,在面对信噪比极端低下的目标时,往往由于积累增益不够高而失效[5]。而相参积累能将信号相干相加以获得相参积累增益,从而提高检测性能[6]。但相参积累需要使用所有积累脉冲的相位信息,所以必须明晰积累脉冲间的相位变化,保证相位一致性[7]。文献[8]对于无线通信系统中的载波同步做了大量研究,基于雷达与无线通信的系统结构高度相似性,可在雷达系统中实现通信技术的优势利用[9],以保持回波信号的相干性。对于雷达,文献[10]提出一种新的补偿方法,计算复杂度较低,能补偿回波信号相位的变化,补偿后脉冲间信号的相位一致,可以相干相加。虽然现有雷达一般都采用相参积累技术[11-12],但这种相参积累是对信号的包络进行积累,积累后的信号再进行非相干检测,仍旧损失了信号的部分相位信息。

对于目标的RCS起伏特性,通常使用起伏目标模型来估计目标起伏的影响并进行数学上的分析。目前的研究,如文献[4]和[13]等,大都是针对非起伏目标进行相参积累。但实际上,目标往往都具有起伏特性,针对隐身飞机等起伏目标的相参积累研究,其实际应用价值也更高[14]。大多数起伏目标的统计特性由卡方分布表述,现有模型中,目标统计特性服从卡方分布且在理论上比较成熟的有4个常用的Swerling[15]模型。该模型对于一些导弹、飞机等目标的拟合性很好,常被用于分析雷达对目标的检测性能[16]。非相干检测可以运用于Swerling的四种起伏模型,但是相干检测只能用于Swerling Ⅰ、Ⅲ型,这是因为Swerling Ⅱ、Ⅳ型起伏目标脉冲与脉冲间的目标幅度不相关(快起伏),无法保持相位相干性[17]。但根据文献[18]的研究表明,对于一定起伏频率范围内的快起伏目标,长驻留信号能够很好地起到平滑作用,减小目标起伏带来的影响[19],相干检测或可应用到快起伏模型中。

综上,对抗隐身飞机等目标的低RCS特性需要相参积累,而对抗其RCS起伏特性需要高效的起伏目标检测方法。若能将相干检测应用于起伏目标,并对脉冲进行积累,就能充分利用回波信号的相位信息,提高雷达对这类目标的检测概率,有效地应对隐身飞机等起伏目标的挑战。本文在分析非相干检测性能的基础上,从检测原理出发,提出将相干检测应用于起伏目标以提高雷达检测性能,基于重积分方程,推导了Swerling Ⅰ、Ⅲ型起伏目标相干检测概率计算公式。并通过仿真验证,对比分析了两种检测方式的检测性能和起伏损失。除Swerling模型外,常用的目标起伏模型还有对数正态分布模型和莱斯分布模型等。文献[20]和[21]还针对隐身飞机等目标的RCS起伏统计特性进行了专门研究。选用的起伏模型越精确,越能反映隐身飞机等目标的RCS特性[22],应用相干检测后也越能提高雷达对于隐身飞机等目标的检测概率。本文安排如下:第2部分,给出了起伏目标模型,第3部分,分析非相干检测原理与性能,第4部分,分析相干检测原理及其非起伏目标性能,第5部分给出起伏目标的相干检测公式,第6部分通过仿真,验证了起伏目标相干检测公式的准确性,并对比非相干检测进行分析,最后给出结论。

2 起伏目标模型

雷达目标通常由多个散射体组成,通过对来自单个散射体,既包含幅度信息又包含相位信息的接收信号采用相干求和的方法,就可以计算出目标的回波幅度。对于静止目标,回波幅度通常是固定值,但运动目标相对雷达视线的姿态角会不断变化,使散射体子矢量合成时,各自的相对相位随机变化,从而产生回波幅度起伏。

通过特定的波形设计和对回波信号幅度与相位的处理、分析和变换,可以得到目标RCS及其起伏统计模型,这可以表征雷达目标的固有特征,所以雷达回波的起伏总是与雷达目标的RCS相联系。由于雷达需要探测的目标十分复杂而且多种多样,很难准确地得到各种目标截面积的概率分布和相关函数,通常是用一个接近而又合理的模型来估计目标起伏的影响并进行数学上的分析。

文献[23]提出χ2分布模型且指出,若其参数设置得当,可用于近似几乎其他所有模型。χ2分布模型为:

(1)

经典的Swerling模型把典型的目标起伏分为四种类型,且扫描至扫描间都是完全不相关的,其中Swerling Ⅰ、Ⅱ型和Ⅲ、Ⅳ型分别有相同的概率密度函数。χ2分布模型包含了传统Swerling模型,但考虑到相干检测只能用于Swerling模型中的Ⅰ、Ⅲ型,且为对比分析非相干检测性能,本文只分析Swerling Ⅰ、Ⅲ型,即自由度为2、4的卡方分布模型[24]。

2.1 Swerling I型

根据文献[25],Swerling Ⅰ型表示由多个均匀独立散射子目标的组合,典型目标如前向观察的小型喷气飞机等。它的起伏特性为慢起伏,接收到的目标回波在任意一次扫描期间都是恒定的(完全相关),但是从一次扫描到下一次扫描完全是独立的(不相关的)。假设不计天线波束形状对回波信号幅度的影响,截面积σ服从自由度为2的卡方分布:

(2)

由于回波信号幅度A在一次扫描内有恒定的幅度值,扫描与扫描间则为瑞利分布,由于A2=σ,所以关于回波信号幅度A的概率密度函数为:

(3)

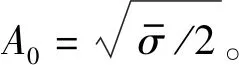
2.2 Swerling Ⅲ型

Swerling Ⅲ型表示一个占支配地位的大随机散射体与其他均匀独立散射体组合的目标,典型目标如螺旋桨飞机及直升机等,它的起伏特性也是慢起伏,其RCS服从自由度为4的卡方分布:

(4)

对应回波信号幅度A的概率密度函数为:

(5)

3 非相干检测原理与性能

3.1 非相干检测原理

假定噪声是均值为0,功率为ψ2的加性高斯白噪声,且和幅度为A的正弦信号是不相干的。正弦信号功率为A2/2,单个脉冲的信噪比可定义为SNR=A2/2ψ2。传统雷达采用非相干检测,根据雷达经典理论,其回波信号幅度的概率密度函数为[25]:

(6)

r为回波信号加噪声的包络,I0(β)是宗量为β的零阶修正贝塞尔函数:

(7)

式(6)是一个莱斯分布函数,如果SNR=0时,即只有噪声输入的时候,变为瑞利分布:

(8)

当SNR非常大,即接收机输入为回波信号和加性高斯白噪声时,式(6)可近似成均值为A,方差为ψ2的高斯分布:

(9)

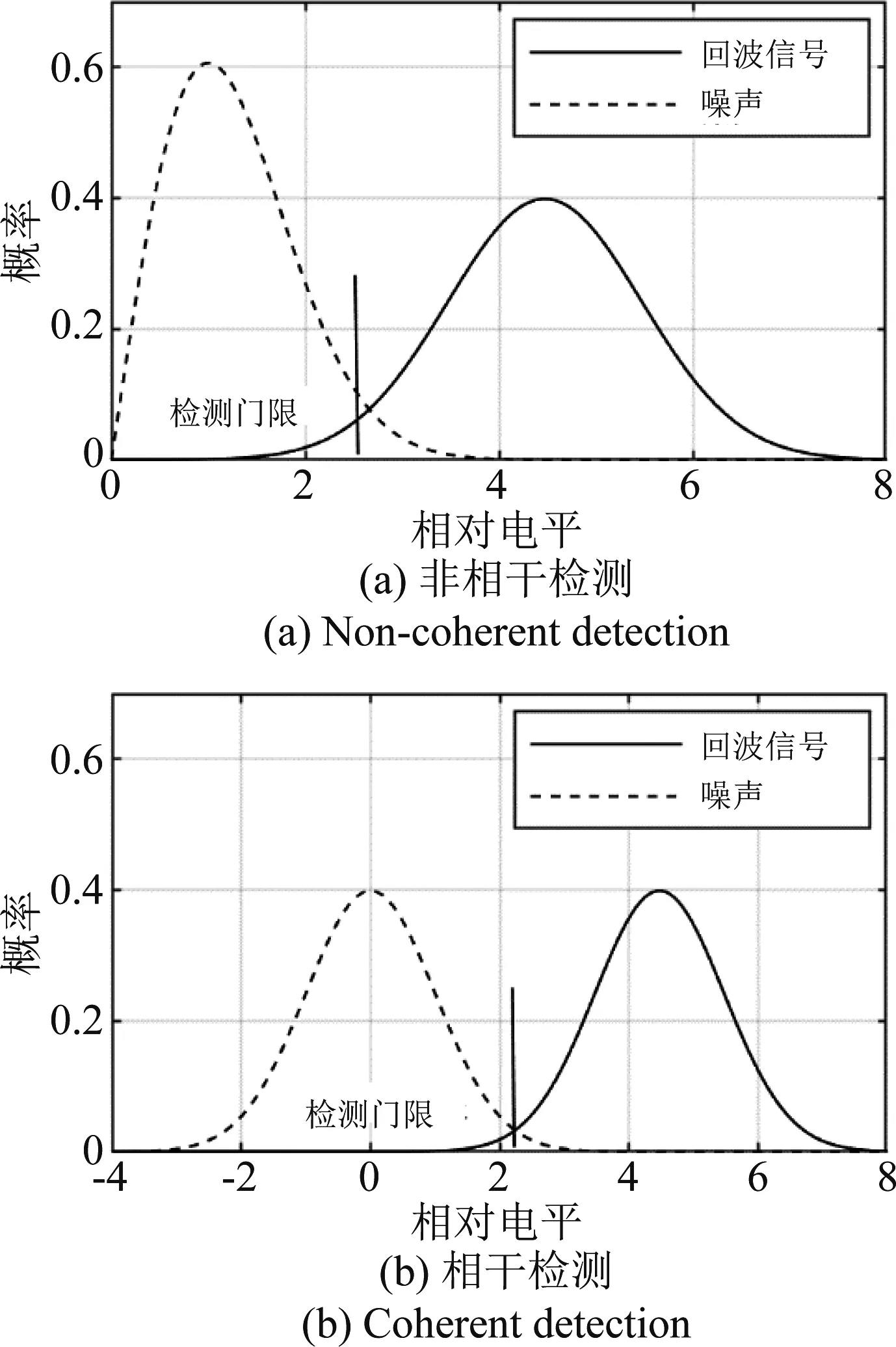
图1 回波信号和噪声概率密度分布图Fig.1 Probability density distribution of echo signal and noise

以纵轴表示概率,横轴表示相对电平,采用非相干检测时,若SNR为10 dB,给定噪声功率为1,回波信号和噪声的概率密度分布如图1(a)所示。

3.2 非起伏目标检测性能

目标RCS的大小与雷达的检测性能有直接关系,在工程计算中常把RCS视为常数,即非起伏目标。当噪声和回波信号一起输入到接收机时,对非起伏目标采用非相干检测,根据文献[17]和[25]可知,虚警概率为:

(10)

式(10)中,若已知虚警概率PF,非相干检测门限VTN可表示为:

(11)

检测概率为:

(12)

式(12)计算非常复杂,但如果给定的虚警概率较小,而要达到的检测概率很大时,可用多种近似方法代替,目前最精确的近似值为[26]:

(13)

erfc(z)为补误差函数:

(14)

在雷达检测中,一般采用奈曼-皮尔逊(Neyman-Pearson)准则:先设定一个虚警概率,然后使得检测概率最大。给定虚警概率PF时,式(13)是关于单次检测概率PD的表达式,它是关于SNR的函数。

(15)

式(15)中,

(16)

上式为不完全伽马函数的皮尔逊形式,VTNI表示非相参积累的检测门限,即:

VTNI=Γ-1(1-PF,N)

(17)

式(17)中I-1表示不完全伽马函数的反函数,检测概率为:

(18)

3.3 起伏目标检测性能3.3.1 Swerling Ⅰ型

Swerling Ⅰ型起伏目标的非相干检测概率公式由Swerling提出:

PD=e-VTN/(1+SNR),N=1

(19)

(20)

3.3.2 Swerling Ⅲ型

Swerling Ⅲ型起伏目标的非相干检测概率公式由Marcum提出,当脉冲积累数N=1或2时,检测概率为:

(21)

(22)

式(21)中,N=1时VT=VTN,N=2时VT=VTNI;当N>2时,检测概率为:

(23)

上式和式(20)都是对信号进行非相参积累后再进行非相干检测,完全未利用回波信号的相位信息。

4 相干检测原理及其非起伏目标检测性能

4.1 相干检测原理

在隐身飞机等起伏目标的挑战下,传统非相干检测雷达的性能已经远远达不到作战需求。通过增大发射功率等途径提高检测性能往往也受制于战场环境,这就需要从雷达检测原理出发,研究如何提高雷达的检测性能。

雷达的检测概率取决于检测门限和检测信噪比,要提高雷达的检测概率,就需要降低检测门限或者增加信噪比。雷达采用非相干检测时,噪声服从瑞利分布,回波信号服从高斯分布。降低检测门限可提高检测概率,但也会造成虚警概率的增加,往往得不偿失。根据文献[25],对于增加信噪比,如果依据雷达距离方程考虑雷达的“硬”对抗,方法仅包含两类:增大有效发射功率、减小接收系统噪声。由于电子对抗措施的存在,增大有效发射功率太易暴露且易遭受攻击,而减小接收系统噪声往往依赖于材料技术的进步,随着高电子迁移率场效应管(High Electron Mobility Transistor, HEMT)的大量采用,接收系统噪声水平难以再大幅降低。

在以上两种增加检测概率的方法均受限制的情况下,要提高雷达的检测性能,就需要从检测的基本原理出发,重新设计目标存在和目标不存在时的两个概率密度函数。根据雷达原理可知,雷达的检测方式有两种,即非相干检测和相干检测。非相干检测只利用了回波信号的振幅信息,而相干检测不仅利用了振幅信息,还利用了其相位信息。对信号的先验信息知道得越多,检测性能越好,所以相干检测的性能理应优于非相干检测。

非相干检测时,变量r表示回波信号加噪声的包络;假定回波信号完全相干,对于相干检测,已知信号的相位信息,此时r表示回波信号和噪声的综合幅度。若雷达采用相干检测,当有回波信号时,其幅度的概率密度函数是均值为A,方差为ψ2的高斯分布:

(24)

当只有噪声时,是均值为0,方差为ψ2为高斯分布:

(25)

采用相干检测时,仍旧给定SNR为10 dB,噪声功率为1,回波信号和噪声的概率密度曲线如图1(b)所示。对比图1(a),噪声与回波信号的概率密度函数分得更开,其交点处概率值更低,也更容易选择合适的检测门限,达到更大的检测概率。

4.2 非起伏目标相干检测性能

对于非起伏目标,相干检测的检测概率要高于非相干检测,文献[29]已经给出了证明。虚警概率为:

(26)

式(26)中VTC代表相干检测门限,若已知虚警概率时,可表示为:

(27)

式(27)中erfc-1(z)为补误差函数的反函数,检测概率为:

(28)

检波器以前进行的积累称为相参积累,检波器不仅利用了回波信号的幅度信息,还利用了相位信息。在理想情况下,对N个回波脉冲进行相参积累,积累后的信噪比可以改善N倍,积累后的信噪比变为(SNR)CI=N×SNR,(SNR)CI为N个脉冲相参积累后的信噪比,将式(28)的SNR替换为(SNR)CI即为相参积累时的检测概率。

需要指出的是,非相干检测时,相参积累只是在短时内忽略了回波信号的相位变化,注定了积累时间不会太长。而相干检测时,保证了回波信号的相位始终相关,可积累的时间更长。

对回波信号先进行相参积累,对积累后的信号进行相干检测,完全利用了其相位信息,因而能达到的检测概率也更大。

5 起伏目标相干检测性能

对于起伏目标的相干检测,回波信号可视为目标RCS变量σ和综合幅度r的联合概率密度函数。用f(σ)表示目标RCS的概率密度函数,f(r)表示综合幅度的概率密度函数,所以联合概率密度函数为f(r,σ)。根据简单的概率论知识,得到f(r)需要用到以下关系式:

f(r,σ)=f(r/σ)f(σ)

(29)

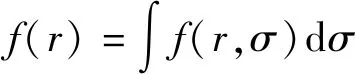
(30)

将式(29)代入式(30)可得

(31)

要求得起伏目标相干检测的检测概率,实质上是求二重积分的解。先对f(σ)从0至无穷大积分,得到综合幅度r的一维概率密度函数f(r),再对f(r)从检测门限VTC到无穷大积分即可得到起伏目标的检测概率。同式(13)一样,在给定虚警概率时,所得到是单次检测概率PD的值,是关于SNR的函数。

又因为目标RCS与回波功率成比例,若以回波信号幅度A为变量,检测概率的求解方式相同,式(31)变为:

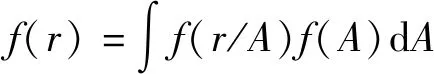
(32)

N个脉冲积累后进行相干检测,单个脉冲信噪比为(SNR)CI,将A固定不变,根据信噪比定义可得脉冲积累后的ψ,带入式(27)可得VTC,再根据式(31)和(32)可得脉冲积累时的相干检测概率。

计算检测概率前,首先要知道检测门限值。非相干检测的门限值计算,单个脉冲检测时为式(11),脉冲积累时为式(17),需要计算不完全伽马函数的皮尔逊形式的反函数等复杂公式,大大增加了计算的复杂度。而对于相干检测,其检测门限的计算公式为式(27),对比于非相干检测,公式数量少,计算复杂度低。在检测方式相同时,检测门限值只与虚警概率和脉冲积累数有关,而与目标是否起伏无关。

基于重积分方程的相干检测,实际计算时只需求得二重积分的解,且计算方法具有通用性。以RCS变量σ为例,根据不同的起伏模型,将对应的f(σ)带入式(31),可得到不同起伏目标的检测概率。相对于起伏目标的非相干检测复杂的计算公式,公式简洁且计算复杂度低。

综上,对于起伏目标,相干检测的检测门限和检测概率的计算难度均小于非相干检测。下面以Swerling型起伏目标为例,对起伏目标相干检测性能进行分析。

5.1 Swerling Ⅰ型

根据起伏目标相干检测概率计算方法,对Swerling Ⅰ型起伏目标信号进行相干检测,回波信号的概率密度函数按RCS形式可表示为:

(33)

将式(2)、(33)带入式(31),可得:

(34)

根据式(32),按幅度形式可以表示为:

(35)

所以,对Swerling Ⅰ型起伏目标进行相干检测,检测概率为:

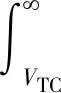
(36)

5.2 Swerling Ⅲ型

对Swerling Ⅲ型起伏目标进行相干检测,回波信号的概率密度函数按RCS形式仍为式(33),将式(4)、(33)带入式(31)可得:

(37)

根据式(32),按幅度形式,回波信号的概率密度函数可以表示为:

(38)

所以,对Swerling Ⅲ型起伏目标进行相干检测,检测概率为:

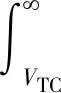
(39)

6 仿真验证与分析

对非起伏目标进行非相干检测时,式(13)为单个脉冲非相干检测理论值,式(18)为脉冲积累时的理论值;相干检测时,式(28)为理论值。对于Swerling Ⅰ型起伏目标,非相干检测时,式(19)为单个脉冲非相干检测的理论值,式(20)为脉冲积累时的理论值;相干检测时,式(36)为理论值。对于Swerling Ⅲ型起伏目标,非相干检测时,脉冲积累数N=1、2时,式(21)为理论值,N>2时,式(23)为理论值;相干检测时,式(39)为理论值。

6.1 相干检测仿真验证

本次仿真主要通过MATLAB对推导的相干检测公式进行仿真验证及分析,仿真时假设目标回波完全相干。对于三种目标的非相干检测和非起伏目标的相干检测,MATLAB中已经有内置函数rocpfa,且其理论已经相当成熟,因此不再对非相干检测进行仿真验证。对于起伏目标相干检测的理论值,主要用到的函数为erfcinv和integral2,前者对应erfc-1(z),可计算出检测门限,后者为二重积分函数。已知检测门限时,根据式(36)、(39)可计算出检测概率。

下面对非起伏目标和Swerling Ⅰ、Ⅲ型起伏目标的相干检测,通过MATLAB进行仿真验证。对于非起伏目标,理想情况下,经相干检测后,在接收机输出处,回波信号的综合幅度服从方差为ψ2,均值为A的高斯分布。对于Swerling Ⅰ、Ⅲ型起伏目标,回波信号的综合幅度在扫描与扫描间分别服从自由度为2和4的卡方分布,相干检测后仍旧服从高斯分布。

对于非起伏目标的相干检测仿真,随机产生一定长度的0、1信息序列,0代表无信号,1代表有回波信号且幅度为1,输入至高斯信道模型,信道输出序列是被干扰了的码字序列。根据奈曼-皮尔逊准则,以SNR为参数,给定虚警概率,根据虚警概率求出检测门限,分别对被干扰了的码字序列进行门限判决,高于门限的信号判定为回波信号,统计出正确检测数,最后除以初始回波信号数,多次仿真后求平均数,得到不同SNR对应的检测概率。

对起伏目标相干检测仿真时,生成的“1”码元需要先输入至卡方分布模型,得到自由度为2或4,平均幅度为1的码字数列后,再输入至高斯信道模型进行门限判决和统计检测概率。

根据文献[27],雷达通常工作时,虚警概率PF的值一般非常小,根据系统的种类不同,PF的典型值不会超过10-3,通常介于10-6和10-8之间,仿真时仍根据这个结论设定虚警概率值。

仿真分为两部分:单个脉冲检测时,分别给定虚警概率PF为10-2、10-4和10-8,以SNR为参数,研究虚警概率对检测性能的影响;脉冲积累时,虚警概率固定为10-8,给定脉冲积累数N分别为10和50时,以SNR为参数,研究脉冲积累数N对检测性能的影响。

对于非起伏目标和Swerling Ⅰ、Ⅲ型起伏目标的相干检测,如图2、图3和图4所示。单个脉冲检测时,给定不同的虚警概率,以SNR为参数,在SNR相同时,相干检测的检测概率均大于非相干检测。也可以这样说,要达到相同检测概率,相干检测所需的SNR均小于非相干检测。同时,对于两种检测方式,给定虚警概率越小,达到相同检测概率所需的SNR越高。

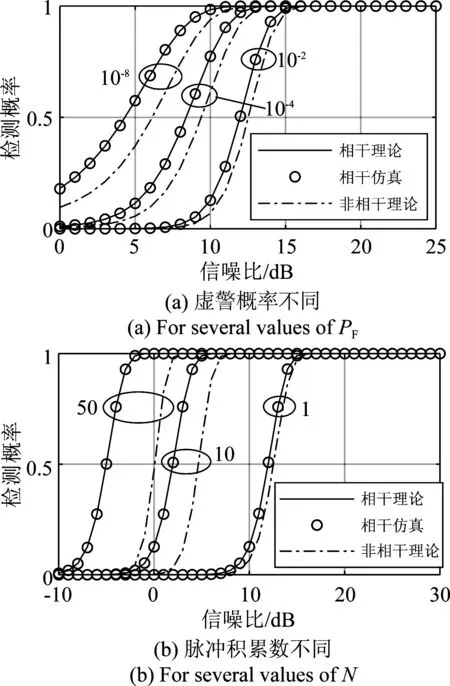
图2 单个脉冲信噪比对应的检测概率(非起伏)Fig.2 Probability of detection versus single pulse SNR. Non-fluctuating targets

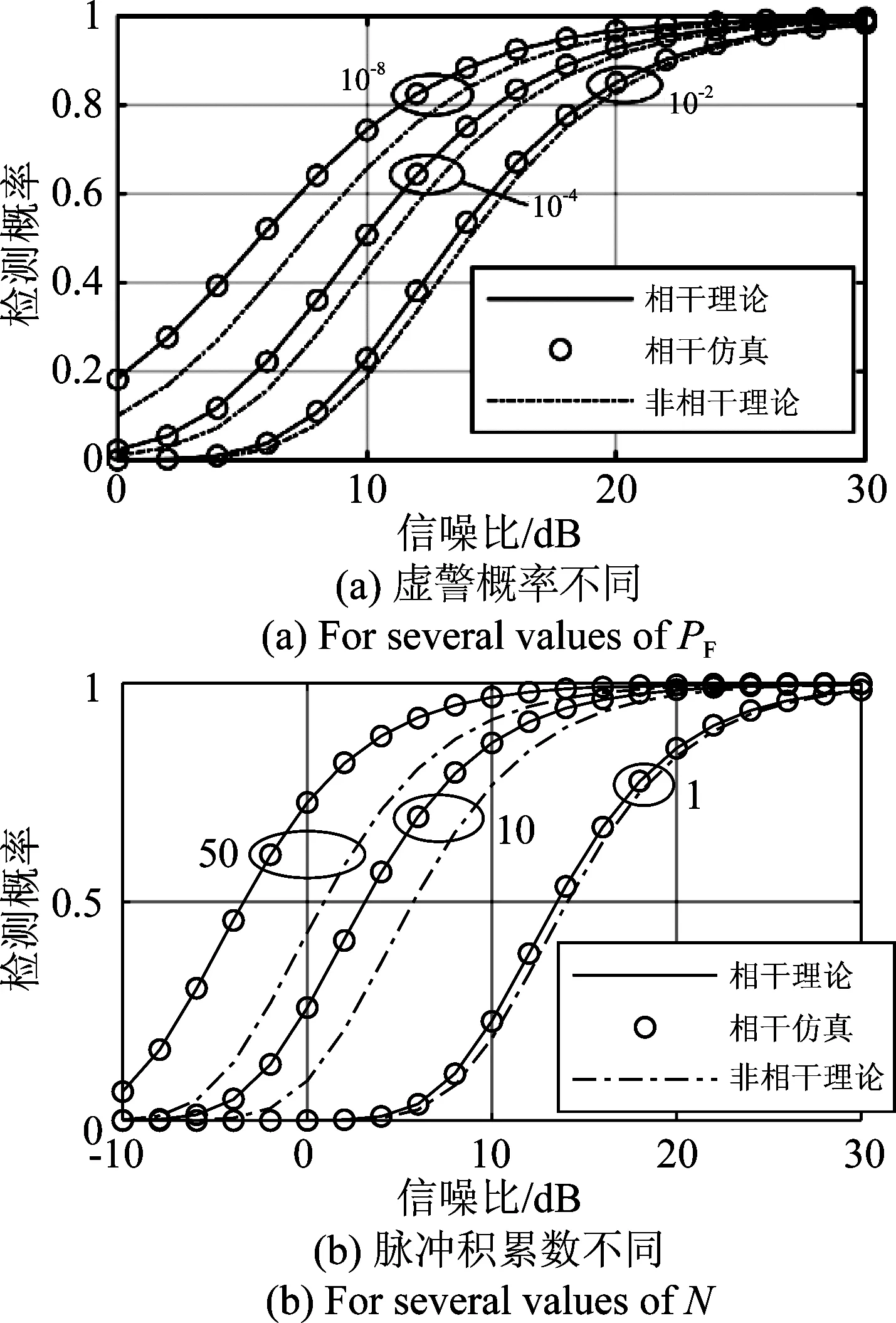
图3 单个脉冲信噪比对应的检测概率(Swerling Ⅰ型)Fig.3 Probability of detection versus single pulse SNR. Swerling Ⅰ

脉冲积累时,虚警概率固定为10-8,给定不同的脉冲积累数,以SNR为参数,SNR相同时,相干检测的检测概率均大于非相干检测。换句话说,要达到相同检测概率,相干检测所需的SNR均小于非相干检测。起伏目标的脉冲积累改善和非起伏目标相同。

图4 单个脉冲信噪比对应的检测概率(Swerling Ⅲ型)Fig.4 Probability of detection versus single pulse SNR. Swerling Ⅲ

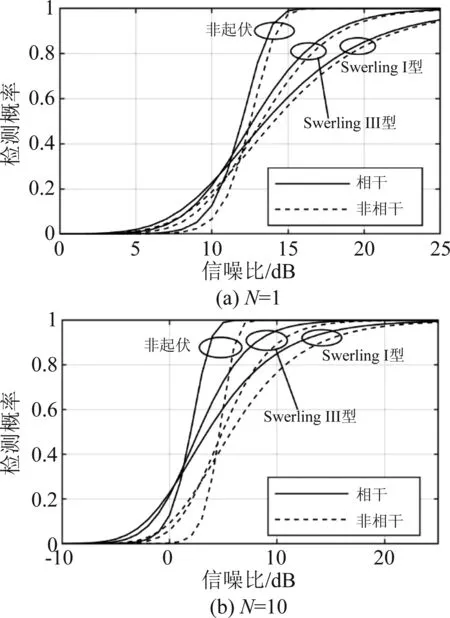
图5 单个脉冲信噪比对应的检测概率对比Fig.5 Probability of detection versus single pulse SNR.Non-fluctuating versus Fluctuating

综上,对于非起伏目标和起伏目标,分别给定相同的虚警概率和脉冲积累数,相干检测的性能均优于非相干检测,仿真结果验证了理论推导。

6.2 起伏目标与非起伏目标对比

对于非起伏目标和Swerling Ⅰ、Ⅲ型起伏目标,给定虚警概率为10-8,分别给定脉冲数N为1、10,以SNR为参数,要达到的检测概率为0.9时,所需的单个脉冲信噪比SNR如表1所示。

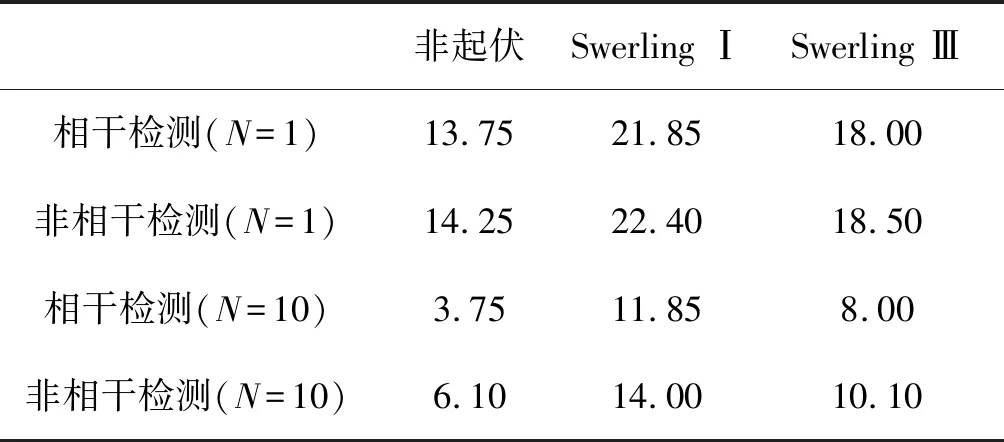
表1 检测概率为0.9时所需的单个脉冲信噪比

N为1和10时,非相干检测所需的SNR均大于相干检测。在N由1增加为10,分别对Swerling Ⅰ、Ⅲ型起伏目标进行相干检测,要达到相同检测概率时,所需的SNR减小了10 dB,而非相干检测所需的SNR的减少量小于10 dB。三种目标模型,脉冲积累数N为10时,相对于非相干检测,相干检测所需的SNR均减小了大约2 dB。

6.3 两种检测方式的起伏损失

目标的起伏引起目标RCS变小,进而造成SNR变小,检测概率随之大幅降低。起伏损失定义为给定相同虚警概率和检测概率,起伏目标相比于非起伏目标SNR额外增加的值。

本文参考了文献[17]的提出的计算方法,该方法的误差可以控制在0.005 dB以内。对非起伏目标和Swerling Ⅰ、Ⅲ型起伏目标分别计算出对应的检测概率PD的SNR,在检测概率相同时,用起伏目标对应的SNR减去非起伏目标的SNR即为对应检测概率PD的起伏损失。本文利用这个方法分析了相干检测和非相干检测的起伏损失。

给定虚警概率PF为10-8,单个脉冲检测时,所得结果如图6所示:在检测概率较低时,非相干检测的起伏损失值会略小于相干检测;在检测概率较大时,起伏损失趋于一致。

图6 起伏损失与检测概率的关系Fig.6 Fluctuation loss versus detection probability

对起伏损失的分析说明,相干检测可以达到比非相干检测更高的检测概率,而两者承受的起伏损失却近似相等,所以其性能更好。

7 结论

本文给出了基于积分方程计算起伏目标相干检测概率的方法,并以Swerling Ⅰ、Ⅲ型起伏目标为例,推导出了其相干检测概率计算公式。通过仿真验证,得到以下结论:对于同一起伏目标模型,给定相同虚警概率和脉冲积累数:a)以信噪比为参数,采用相干检测的检测概率要高于非相干检测,且脉冲积累数越大,检测概率更高;b)以检测概率为参数,在检测概率较大的情况下,相干检测和非相干检测的起伏损失是近似相等的。综上,对于起伏目标,相干检测的检测性能要优于非相干检测。虽然Swerling Ⅰ、Ⅲ模型已经不太适合于现代飞机,但其作为自由度分别为2、4的卡方分布,改变自由度即可拟合其他起伏目标模型,因而本文对于提高隐身飞机等目标的检测概率有一定参考意义。实际应用过程中,应该根据目标起伏特性选择最合适的起伏模型和脉冲积累数,以期达到最佳的检测性能。