屋顶风机隔振设计及垫板参数对隔振性能的影响

熊志远，宋瑞祥，赵娜，赵阳，邬玉斌

(北京市劳动保护科学研究所，北京100054)

0 引言

风机被广泛应用于各行各业，为国民经济的发展做出了重要贡献。但是，风机运转时产生的剧烈振动不仅威胁着风机自身的安全运行，而且辐射的噪声也影响着人们的身心健康。

图1是隔振风机。风机与电动机均固定在钢基座上，电动机输出轴通过变速器与风机转轴相连，钢基座安装在6个隔振器上，隔振器下端凸出边缘预留有螺栓通孔，经预埋螺栓或膨胀螺栓可将隔振器下端固定在基础上。风机运转时，隔振器将风机的振动与基础隔开，减小传递到基础的振动。

对于风机的隔振设计，目前已取得了不少成果。李月桂[1]对安装在氧气转炉炼钢车间的、为转炉除尘的D-700-13大型鼓风机进行了隔振设计，采用上海青浦淀山湖减振器厂生产的ZT型阻尼弹簧隔振器，经2 a多试运行，取得了良好的隔振效果。郑明忠[2]将冶炼排烟引风机与混凝土基座联成一个整体，在整体结构与地基之间经设计而安装高性能橡胶隔振块，取得了良好的隔振降噪效果。李献梅和窦晓东[3]、李淑雅与桑惠斌[4-5]在喷雾干燥工程项目中，对安装在厂房4层楼板上的离心式引风机进行了隔振设计。设计过程中，首先选用圆柱形橡胶隔振器，然后对隔振器尺寸进行校核。卫辉等[6]对某风机隔振系统进行了理论与仿真分析，给出了隔振器刚度系数与阻尼系数对风机隔振性能的影响规律，并基于风机结构的非对称性优化了隔振器参数。李爱芹和矫云学[7]建立了Y6型引风机铅垂方向的力学模型及数学模型，通过计算与系统特性分析，确定了一种选择隔振器的方法。姚丙义[8]对风力发电机组的冷却风机进行了隔振设计，提出了一种切实可行的风机用隔振器的选型设计方案。

上述文献中的风机隔振设计过程大致可归纳为如下3步：1）第1步。利用预期振动传递率η，基于公式ωn= ω[η/(1+η)]0.5（ω为激励频率）确定风机隔振体系的固有频率ωn。2）第2步。通过K=Mωn2（M为风机或风机与基座质量）确定隔振层总刚度K；通过C=2ζ(MK)0.5（ζ为阻尼比）确定隔振层总阻尼系数C。然后，依据现有隔振器生产厂家的工程手册或产品样本匹配成型的隔振器产品，并以该产品参数作为最终参数进行验算。3）第3步。核算风机、基础的振幅，必要时对隔振参数进行反复调试，以满足设计要求。

但是，对于图2所示的屋顶风机，由于其特殊的安装要求，隔振设计时，不能按上述步骤去选择成型的隔振器产品及作进一步的验算。屋顶风机常用于库房、工矿厂房、电站、车站、体育馆等的通风换气。屋顶风机安装时，风机泛水帽（基座）与屋顶泛水（基础）之间必须密封连接。图1中，相邻两隔振器之间有很大的间隙，远不满足基座与基础密封的条件。密封性能是屋顶风机运行可靠的重要指标[9]，密封效果不好，杂物、灰尘等容易进入风机底部的通风口，导致叶轮损坏、电动机故障，甚至导致叶轮飞出砸伤人员[10]。

图1 隔振风机

图2 安装于屋顶的风机

风机厂家的操作说明提到：在风机泛水帽与屋顶泛水之间，依据泛水上表面尺寸铺设5～8 mm厚弹性垫。但至今仍没有发现有关屋顶风机较为完整的隔振设计资料或文献。鉴于此，本文针对屋顶风机的隔振提出一种设计思想，并探讨隔振垫参数对隔振性能的影响规律，为在种类繁多、型号各异的橡胶或聚氨酯等隔振材料中选择、裁剪满足预期隔振效果的屋顶风机弹性隔振垫板提供理论参考依据。

1 屋顶风机的结构、参数及安装

图3是屋顶风机的结构及安装示意图。图3左上为风机结构示意图，风筒内壁对称固定有2根支撑杆，两支撑杆共同固定、支撑驱动电动机，电动机输出端通过联轴器与叶轮相连，风筒上部为圆形风帽，下部为正方形泛水帽，泛水帽内侧边长为1310 mm，深为80 mm。风机质量为277 kg，电动机转速为1440 r/min。图3左下为泛水结构示意图，泛水是屋顶的一种建筑结构，即在屋顶开洞的外侧向上翻起的防水翻口。泛水高度依当地降水量而定，一般为250～500 mm。正方形泛水外侧边长为1300 mm，内侧边长为1140 mm。泛水中间安装有多片联动的铝制重力止回风阀，可有效防止室外空气倒灌。图3右侧为风机安装在泛水上的示意图。安装时，风机通过其下部的泛水帽扣压在泛水上，按照密封、稳定的要求，在泛水与泛水帽之间添加外侧边长为1300 mm、内侧边长为1140 mm的正方形弹性隔振垫，其面积为13002-11402 =390400 mm2，风机厂家常给出弹性垫的厚度为5～8 mm，但没有给出理论计算依据。

图3 屋顶风机的结构及安装示意图

2 屋顶风机的隔振设计

2.1 单自由度阻尼振动系统的振动传递率

将上述屋顶风机隔振系统简化为图4所示的单自由度阻尼振动模型。弹性垫简化为线性弹簧、阻尼器的并联结构。弹性垫将风机的振动与泛水隔开，减小传递到泛水的振动。泛水响应力幅值与输入激励力幅值之比定义为振动传递率η[11-12]，表示为

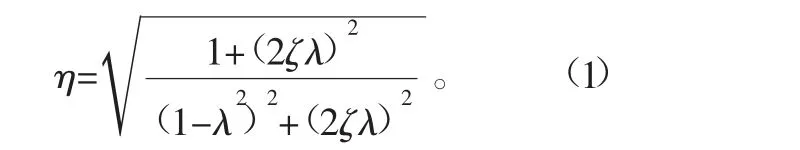
图4 屋顶风机隔振系统简化模型

式中：ζ为阻尼比；λ为激励频率ω与系统固有频率ωn之比，即

式中：m为风机质量；k为弹性垫垂向静刚度。

振动传递率η能定量衡量弹性垫隔离振动的程度。η越小，隔振效果越好；η越大，隔振效果越差。

2.2 弹性垫垂向静刚度

图5 弹性垫受压变形示意图

图5 是安装在泛水上表面的弹性垫受压变形示意图。垫板面积为s，厚度为h，受压后厚度方向发生Δh的位移。

垫板垂向静刚度k为力F与沿力方向引起的位移Δh之比：

2.3 含有垫板参数的振动传递率

将式（9）代入式（3），式（3）代入式（2），再将式（2）代入式（1），可得含有垫板参数的振动传递率为

从式（10）可以看出，振动传递率η与两类参数有关，一类是与风机有关的参数，如风机质量m、激励频率ω；另一类是与弹性垫有关的参数，如厚度h、面积s、静弹性模量E及阻尼比ζ。

由于屋顶风机的隔振不能选用成型的隔振器产品，故选择奥地利格士纳（Getzner Werkstoffe）公司生产的、隔振性能优异的成捆聚氨酯弹性隔振垫[13]。每种型号垫板宽为1.5 m，展开后长为5 m，有12.5、25.0、37.5 mm等3种厚度可供选择，面积可根据需要任意裁剪。风机、SR11型号聚氨酯弹性垫的已知参数及设计要求如表1所示。

表1 屋顶风机隔振系统已知参数及设计要求

隔振效率I与振动传递率η之间的换算关系为

将表1中的I=85%代入式（11），可得η=0.15。然后，将η=0.15及表1中相关参数代入式（10），计算得垫板厚度h为34.79 mm。

3 垫板参数对隔振性能的影响

从式（10）可知，当风机质量m与激励频率ω一定时，隔振垫的各参数（h、s、E、ζ）均对振动传递率η有影响，但是仅从式（10）无法直接判断它们之间的变化关系。基于式（10）及表1中的相关参数，在只允许垫板1个或2个参数变化，其余参数均不变的情况下，通过图形定量分析垫板各参数对振动传递率的影响规律。

3.1 垫板厚度对振动传递率的影响

将表1 中的相关参数代入式（10），其中只允许垫板厚度h 发生变化，作出如图6所示的垫板厚度与振动传递率的变化关系曲线。

令式（10）等于1，解得

图6 垫板厚度与振动传递率的变化关系

将表1中的相关参数代入式（12），计算得h=7.44 mm。当h＜7.44 mm时，系统不但不能隔振，反而引起振动放大。预期隔振效率I为85%时，其振动传递率η为0.15，对应的垫板厚度h为34.79 mm。如果不对SR11型号弹性垫的厚度进行加工，直接选取h=25 mm，则η=0.209，I=79.1%；h=37.5 mm，则η=0.141，I=85.9%。

从图6可看出，7.44 mm＜h＜25.00 mm时，随着垫板厚度的增加，η急剧下降，隔振效果明显提高；h＞37.5 mm时，随垫板厚度的增加，η下降极微小，隔振效果提高十分缓慢。当h在25.0～37.5 mm之间取值时，既能获得良好的隔振效果，又能降低风机重心和产品成本。

3.2 垫板面积对振动传递率的影响

将h=34.79 mm及表1中的相关参数代入式（10），其中只允许垫板面积s发生变化，作出如图7所示的垫板面积与振动传递率的变化关系曲线。

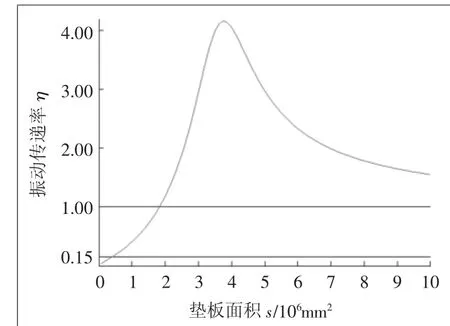
图7 垫板面积与振动传递率的变化关系

令式（10）等于1，解得

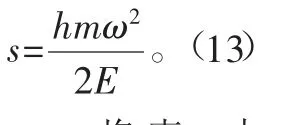
将表1 中的相关参数代入式（13），计算得s =1.83 ×106mm2。当s＞1.83 ×106mm2时，系统引起振动放大。

当0＜s＜1.83×106时，随着s减小，η也相应减小，隔振效果越好。但这只是理论结果，实际上垫板面积不可能取得非常小，因为弹性垫隔振时，需要保证自身压缩应力-应变之间的近似线弹性变形关系。表1中，垫板的静态压缩极限P为0.011 N/mm2，对于277 kg的屋顶风机，垫板最小允许压缩面积为mg/P=246782 mm2。当预期η为0.15时，对应的垫板面积s为390 400 mm2。390 400 mm2远大于246 782 mm2，可见，还可通过减小面积来提高隔振效果，但对于屋顶风机，隔振垫板的面积一般与泛水上表面面积一致。

3.3 垫板厚度和面积对振动传递率的影响

将表1中相关参数代入式（10），其中允许垫板厚度h和面积s同时发生变化，作出如图8所示的厚度h、面积s、振动传递率η三者变化关系曲面。

图8中，①号曲线是η=1的水平平面与h、s、η三者关系曲面的交线。假定垫板面积s取定某一个具体的值时，随着垫板厚度h由0逐渐增加，振动传递率η由1开始急剧上升，经过共振峰后显著下降，与①号线相交后，先下降较为明显，而后下降越来越平缓。其与①号线相交，交点以上为振动放大区，交点以下为隔振区。②号线就是s=390400 mm2时振动传递率η随垫板厚度h的变化关系曲线，即图6所示曲线。

假定垫板厚度h取定某一个具体的值时，随着垫板面积s由0逐渐增加，振动传递率η由0开始逐渐上升，与①号线相交后，也经历一个共振峰（未显示）。其与①号线相交，交点以上为振动放大区，交点以下为隔振区。③号线就是h=34.79 mm时，振动传递率η随垫板面积s的变化关系曲线，即图7中的前段部分。

可见，对于同种材料的垫板，可依据设计结果和实际条件，既可以只调整h或s，又可以同时调整h和s，来多方实现预期隔振效果。

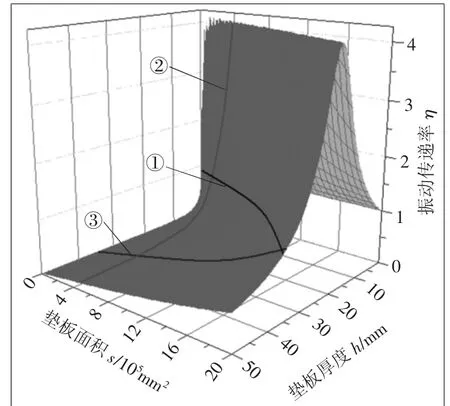
图8 垫板厚度、面积与振动传递率的变化关系

3.4 垫板静弹性模量对振动传递率的影响

将h=34.79 mm及表1中的相关参数代入式（10），其 中只允许静弹性模量E 发生变化，作出如图9所示静弹性模量与振动传递率的变化关系曲线。

令式（10）等于1，解得

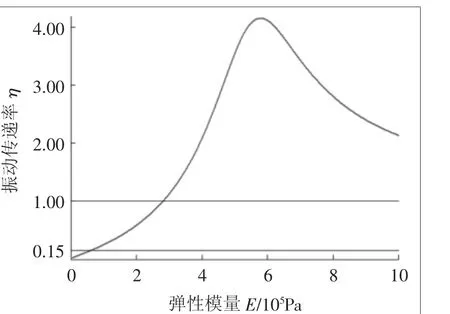
图9 垫板静弹性模量与振动传递率的变化关系

将h=34.79 mm及表1中的相关参数代入式（14），计算得E=2.81×105Pa。当E＞2.81×105Pa时，系统引起振动放大。当0＜E＜2.81×105Pa时，系统处于隔振区，且随着E的减小，η也变小，隔振效果变好。但实际上E不可能取得非常小，即垫板材料不可能十分柔软，它至少要承载得起风机的重力。当预期η为0.15时，对应的静弹性模量E为6×104Pa。

3.5 垫板阻尼比对振动传递率的影响

将式（9）代入式（3）后，再将表1中相关参数代入，计算得固有频率ωn为49.3 rad/s，表1中的激振频率ω=150.8 rad/s，基于式（2）计算得频率比λ=3.06。

将h =34.79 mm及表1中的相关参数代入式（10），其中只允许垫板阻尼比ζ发生变化，作出在频率比λ=3.06的条件下，阻尼比与振动传递率之间的变化关系曲线，如图10所示。

由于有

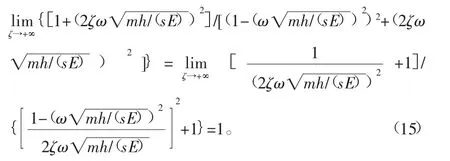
图10 垫板阻尼比与振动传递率的变化关系

由式（10）、式（15）可知，当ζ趋近于正无穷时，振动传递率η的极限等于1。

由图10可知，随着阻尼比ζ的减小，振动传递率逐渐下降，隔振效果增强。而实际上阻尼比ζ一般不取得很小，因为当开、关风机时，激振频率经过固有频率49.3 rad/s时能够起到一定的抑制共振的作用。

4 结语

屋顶风机安装过程中，由于要求屋顶泛水上表面与风机必须密封接触，故不能按常规风机隔振设计步骤去选择已定型的隔振器产品。本文基于单自由度有阻尼振动系统的振动传递率和弹性垫垂向静刚度，进一步导出含有垫板参数的振动传递率，建立垫板参数与隔振效果的直接、连续变化关系。选用奥地利格士纳公司生产的SR11型号聚氨酯弹性隔振垫，在垫板面积满足密封、稳定的条件下，计算出满足预期隔振效率的垫板厚度。同时，探讨了垫板参数对振动传递率的影响规律，得到如下结论：1）垫板厚度必须大于某一临界值时，系统才会产生隔振效果，否则引起振动放大；在隔振区随着垫板厚度的增加，前段区域系统隔振效果提高明显，后段区域系统隔振效果提高很微小；选取适当垫板厚度，既能实现良好的隔振效果，又能降低风机重心和产品成本。2）垫板面积必须小于某一临界值时，系统才会产生隔振效果，否则引起振动放大；面积越小，隔振效果越好；实际上垫板面积不可能取得非常小。3）对于同种材料的垫板，依据设计结果和实际情况，既可以只调整垫板面积或厚度，又可以同时调整垫板面积和厚度，以多方实现预期隔振效果。4）垫板静弹性模量必须小于某一临界值时，系统才会产生隔振效果，否则引起振动放大；垫板静弹性模量越小，隔振效果越好；实际上垫板静弹性模量不可能取得非常小。5）阻尼比趋近于正无穷时，振动传递率的极限等于1；随着阻尼比的减小，振动传递率下降，隔振效果增强；为了对共振起到一定的抑制作用，阻尼比一般不取得非常小。