“以学生为中心”原则下的复变函数与积分变换课程教学设计的若干思考

王凡 孔倩 张新华

摘 要：复变函数与积分变换课程是理工科的一门重要的数学基础课，在学生后续学习其他工科课程中发挥着极其重要的作用。鉴于这门课程的理论复杂性，传统的教学模式往往受学时的限制，教学效果并不理想，因此为提高教学效果，本文提出以学生为中心的原则下课程教学设计的若干思考，即在倡导网络教学的新形势下如何激发学生的学习兴趣、培养学生的学习信心以及提升他们的学习能力。近几年的教学实践表明，这些方法对提高这门课程的教学效果行之有效，受到学生们的普遍欢迎。

关键词：复变函数与积分变换;教学设计;对分课堂;Matlab仿真;学习通软件

众所周知，复变函数与积分变换是理工科各专业的一门重要的数学基础课，它是学生学习农业机械化、力学、自动控制理论、电子技术、自动化、信号处理等诸多课程的先修课，也是解决实际工程问题的有力数学工具。然而，由于这门课是建立在高等数学与数学分析课程的基础之上，其数学公式繁多，理论性较强，因此对初学者而言，它的内容显得难度很大，学生学习的效果往往不容乐观。

鉴于工科学生学好这门课程的重要性，我们做了一些新的尝试，开展了多样化的线上教学模式，并将其与传统的教学模式相结合，充分发挥线上模块化教学与线下集中授课的优点，取长补短。既解决了学时的限制，又拓宽了知识面，也加深了一部分内容的难度和深度，以适应不同专业对该门课程的不同需求。本文是根据多年来这门课的教学经验与学生的学习情况，坚持“以学生为中心”原则，总结若干切实可行的新型教学方法，期待与同行专家学者学习交流。

一、注重激发学生的学习兴趣

本科阶段三门数学基础课：高等数学、线性代数及概率论与数理统计，虽然让学生学习到了丰富的大学数学知识，但由于它们的抽象性与计算复杂性，学生学习效果也是良莠不齐。考虑到它们是考研科目，学生还是会全力以赴去学好这些课程。然而，复变函数与积分变换不是工科学生的考研科目，加上它的理论复杂性，学生的学习动力明显不足，这样在平时教学中，学生比较容易懈怠，集中上课的效果不容乐观，作业完成的质量往往不高。

以上这些是当前学生学习这门课的普遍现象，作为教师，我们需要重视并改变它。为了让课堂的气氛活跃起来，我们以PPT课件和录制小视频的形式给同学们介绍与这门课知识点有关的有趣故事。例如在讲复数的起源时，可先通过PPT课件介绍在复数的产生过程中，那些著名的数学家的故事，了解其人，知道其对复变函数作出的伟大贡献，包括伟大的数学家欧拉，柯西，魏尔斯特拉斯，黎曼等等。简要了解数学史对学习这门课程很有帮助。比如让同学们了解欧拉是如何利用高等数学知识，得到欧拉公式的，而后人又是如何利用三角函数的幂级数展开式给出其严格证明方法，欧拉本身的生平事迹十分励志，特别对于处于信息严重爆炸的今天的学生，会有很强的震撼作用，学生也必然会被欧拉论文成果多产与毅力坚强所吸引。

当学生不再感觉这门课程只是晦涩难懂的时候，我们提出一些有趣的问题。比如，正弦函数与余弦函数在高等数学里有界，它们在复变函数是否仍然有界？复变函数中，指数函数如何定义？指数函数又为什么会具有周期性呢？对数函数为什么会是多值的？这些与高数截然不同的结论，必然激发他们学习复变函数的极大兴趣，于是我们再鼓励学生课余时间在复变函数与积分变换教材中寻找答案，让他们以行动自觉地学习这门课程的相关知识点。

另外，我们也会利用数学软件Matlab仿真来处理一些理论性强的概念如级数、留数、傅里叶变换及拉普拉斯变换等，鼓励学生课余时间也来利用这软件做一些仿真练习，这些形象的教学手段有助于学生加强对复杂公式、概念等的理解与认识。由此激发学生的学习兴趣，让他们感受到我们教师这么做就是为了让他们学习这门课充满乐趣，而不是只有枯燥与困惑。

二、培养学生学习这门课的信心

多年的教学经验告诉我们，切不可在课堂上一味地讲授复变函数与积分变换的知识点。虽然这门课是建立在高等数学与数学分析之上，但很多学生已经忘记甚至记错高等数学中的概念、定义、定理等，甚至搞错解题方法。因此，我们在下次讲授新课前，会提醒学生我们将要学习哪些内容，这些内容与高等数学里哪些内容相似或有关，鼓励同学们课余时间复习相关的高等数学知识，同时预习这门课的新知识点。例如，复变函数与积分变换课程中的极限、连续、导数、级数及其敛散性的判别等，在高等数学中也有此类定义。

我们采用的这种类比的教学方法可以很好地培养学生自发学习与查资料的学习习惯。当他们走进课堂学习新知识点的时候，信心满满;当我们事先设计好问题，在课堂提问的时候，他们也会抢着回答。我们的课堂教学形成了很好的互动氛围，让学生感受到他们就是课堂教学的积极参与者，课堂是他们展现自我才华的舞台。

三、最大可能地提升学生的学习能力

当同学们对复变函数与积分变换课程的学习充满兴趣与信心的时候，作为这门课的教师，我们思考着如何趁热打铁，最大可能地提升他们的理解能力、计算能力及表达能力。具体而言，我们采用对分课堂教学模式。这种教学模式最早是复旦大学张学新教授提出的，它起初主要应用于人数少的文科课程教学。我们采用分组的方法，布置学习任务给每个小组，再结合超星学习通的线上教学平台，也取得了较好的效果。我们的具体做法是，将全班分成若干小组，选择各章的部分小节内容作为他们的自学内容，小组内部互相交流，确定学生代表，利用课堂教学的部分时间，采用板书或者PPT的形式给全班师生讲解，然后全班讨论，最后我们授课教师总结与点评。

例如，我们讲授复变函数的概念与极限，先请学生代表講解复变函数的连续性，然后请其他小组同学讨论该学生代表讲课的优点与不足，最后授课教师点评。我们讲函数解析的充分必要条件，先安排小组同学讲初等函数并举例，大家再讨论，最后我们加以总结。在时间上，我们一般安排学生讲课15分钟，大家讨论5分钟，教师点评与总结25分钟。这样，学生将有20分钟课堂时间展现自我风采，锻炼自己的理解能力与表达能力。这对于学生也是一种很必要的锻炼，离开座位，走上讲台，当一次“老师”，体会自己学会和通过自己的讲解让别人学会的区别，也是学生展现自己的一次难得机会。

这样做的确会占用一部分课堂教学时间，教学大纲中的教学任务如何有效完成呢？我们充分利用超星学习通线上教学平台，将每次上课的内容、课件及相关资料放在平台上，供学生随时查阅。承担复变函数与积分变换教学的所有教师均可提前录制相关教学内容的视频，放在学习通的资料库里，根据每个班级的教学进度按时发放。这样一方面可以弥补课堂教学时间的不足，另一方面对于学生在课下预习和复习时，可以反复观看教学视频，也可以结合自己的实际理解情况，选择跳过某部分视频，直接进行下一个知识点的学习。这种自主选择学习内容的方式受到同学们的普遍欢迎，既照顾学习能力比较强的学生，节约了时间，又可以照顾到接受能力相对薄弱的学生，通过反复观看理解，有疑问随时在平台上提出，老师不再局限于地点的选择，随时随地可以解答疑问。

每章结束以后会进行线上测试，分为系统自评和学生互评两种。系统自评以客观题为主，在题库里随机选择相关题目，学生可多次作答，取最高分数计入该次成绩。系统可以统计出每题的正确率，授课教师可参考统计结果决定是否在课堂上统一讲解该题目。这样可以很好地弥补课时量不足的局限。教师也可以根据测试结果和每次的作业报告及时了解学生对知识点的掌握情况，从而在后面的教学中及时查缺补漏。

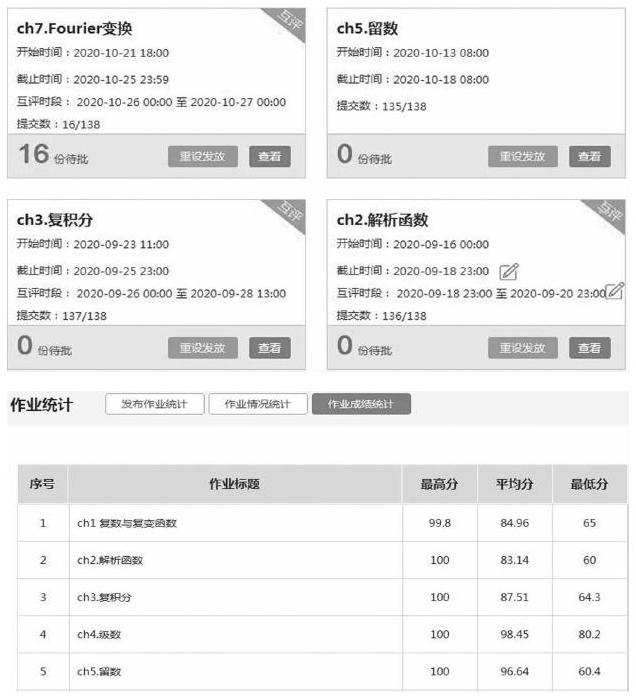
下图是部分作业的发放和统计情况。

对于成绩方面，我们将学生的出勤、讲课质量、线上线下作业的完成情况作为平时成绩考核的重要依据，适当降低期末考试成绩所占的比重，这样更好地激发了同学们的学习自觉性。总之，我们所做的一切都是旨在以学生为中心，激发学生学习复变函数与积分变换课程的兴趣，培养他们敢于挑战这门理论性强的数学课程的学习勇气，进而最大可能性提升他们的理解能力、计算能力及表达能力。这样，他们将努力学好这门课，为其他后续理工科的应用类课程打好基础。教学相长，这也提高了我们教师的业务水平与专业素养。

致谢：作者感谢南京农业大学工学院教改项目《复變函数与积分变量》混合式教学探索与实践（No.2019GQ0502）的资助，也感谢编辑和审稿专家的宝贵建议。

参考文献：

[1]周立芳，卢金.复变函数的课堂教学研究[J].湖州师范学院学报，2018，40（12）：41-44.

[2]杨慧贤.创新能力要求下复变函数积分教学改革思考[J].高教视野，2019，（21）：25.

[3]李志艳.复变函数与积分变换学习兴趣培养[J].读与写（教育教学刊），2019，（10）：19.

[4]刘春媛.复变函数与积分变换应用型课程教学模式改革与探索[J].课程教育研究，2018，（52）：103.

[5]张琼芬，李海权，石凯.工科类专业复变函数与积分变换课程教学改革探索[J].高教学刊，2018，（23）：120-126.

[6]凌浩，郝小健.浅谈复变函数课程之于应用型本科人才培养[J].教育现代化，2019，（93）：13-14.

[7]王洪涛.让“微课程”走进课堂[J].教育教学论坛，2018，（44）：119-120.

[8]王波，于跃.自动化专业复变函数与积分变换教学方法浅析[J].教育教学论坛，2020，（02）：252-253.

基金项目：南京农业大学工学院教改项目《复变函数与积分变量》混合式教学探索与实践（No.2019GQ0502）

作者简介：王凡（1980— ），女，汉族，安徽宿州人，硕士，讲师，研究方向：微分几何。