基于LBM-DEM 耦合方法的突水溃砂运移规律研究

浦 海，郭世儒，刘德俊，许军策，王 健

（1.中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116；2. 新疆工程学院 采矿工程与地质学院，新疆 乌鲁木齐 830091；3.中国矿业大学 力学与土木工程学院，江苏 徐州 221116）

0 引 言

随着我国煤炭开发基地的战略性西移，西部矿区煤层开采时因其独特的地质条件和高强度开采方式涌现出许多工程问题，其中在采掘工作面频发的突水溃砂灾害已成为影响煤矿安全生产的关键问题之一。 高强度开采过程中的扰动促使上覆含水层底部产生裂隙，在裂隙发育形成导水通道后进一步贯通厚松散砂层使水砂混合物涌入工作面是突水溃砂灾害形成的主要方式之一。 在形成导通裂隙后，水砂运移的方式将决定矿井的危害程度，迫切需要研究水砂运移规律，尤其是在形成裂隙通道时，水砂在其内部的流动规律及对通道的扩张影响［1-3］。

近年来，众多学者针对突水溃砂问题在理论分析、相似试验模拟、基础试验验证、数值计算模拟等方面做出大量的研究成果，为深入了解突水溃砂发生机理与灾害防控提供了有意义的参考［4-12］。 基于工程分析角度，张桂民等［13］分析探讨了煤矿钻孔诱发的突水溃砂机理，提出了防治和治理突水溃砂的措施。 许延春等［14］研究了工作面突水溃砂机制，并提出相应的预防措施。 张勃阳等［15］采用流体力学方法，分析煤矿溃砂事故，提出了钻孔溃砂灾害的通用计算方法。 基于试验研究角度，张凯等［16］根据实际工程情况进行了涌砂判据的试验研究，通过渗流试验研究了砂岩的水力特性，得出涌砂发生的临界条件。 李宏杰等［17］进行了突水防砂的实例研究，根据试验结果提出了分层开采、降低上下分层开采厚度等优化设计和技术措施。 袁奇［18］分析了陕北矿区溃砂主要来源，并设计整套试验装置分析突水溃砂现象，摄录了不同砂粒粒径、砂厚和水头高度情况下溃砂剖面特征，直观展示了突水溃砂过程。 杨鑫等［19］采用自主研发的水砂两相高速渗流试验设备，对西部榆横矿区风积砂含水层的起动、溃砂规律及水砂两相高速渗流进行室内试验研究。 提出西部典型矿区风积砂含水层突水溃砂灾害的临界判据，并分析溃砂过程中的能量传递机制。 杨伟峰等［20］设计了水砂混合涌流装置，模拟了覆岩裂隙通道水砂混合突水启动过程及迁移过程，分析了裂缝通道中水砂混合流的突水特征。 高炳伦［21］针对工程中裂隙溃砂问题研制了裂隙溃砂试验系统，实现了单一平直裂隙条件下裂隙溃砂过程的试验模拟。 基于模拟研究角度，王迎超等［22］采用DEM 数值模拟方法建立了固-水两相流动的三维模型，直观地展现了突水溃砂时水砂运移过程。 梁艳坤等［23-24］采用分形理论分析了垮落带破碎岩体的块度分布特征，并利用离散元方法（DEM） 根据破碎岩体的块度分布生成不规则碎石，建立了垮落带破碎岩体溃砂数值模型。

目前针对突水溃砂问题的研究并不透彻，主要原因是地下空间为封闭不可观测系统，地层水砂分布、承压含水层压力、岩层裂隙网络分布等因素难以观测。 加之水砂性质的多样，进行相似模拟试验时选取相似材料过程繁琐，通过试验手段对突水溃砂危害性评估有很大的难度。 数值模拟因其可重复性和直观性等特点，在研究突水溃砂灾害时有明显的优势。

突水溃砂数值模拟中，重点在于针对砂粒及流体选取合适的计算模型，能够将两者进行耦合以得出符合实际的运动过程。 传统的研究方法中将砂看成另一种形式的流相，水砂混合流动看成两相流问题，或者将砂简化为质点，忽略颗粒之间的碰撞及翻转，在分析突水溃砂下水砂在裂隙网络中的运移规律时达不到真实效果。 为使模拟更符合实际问题，笔者采用格子Boltzmann 方法（Lattice Boltzmann Method，LBM） 模 拟 液 相 流 动， 用 离 散 单 元 法（Discrete Element Method，DEM）构建球形砂粒，并采用浸入移动边界法（Immersed Moving Boundary Method， IMB）方法实现流体和砂粒间的耦合，由此模拟砂粒在流场中的流动情况，有效地分析突水溃砂下水砂两相流动运移规律。

1 突水溃砂分析模型

西部矿区煤层开采时突水溃砂灾害的演变过程如图1 所示。 西部矿区煤层开采时剧烈的扰动使上层覆岩形成大量裂隙网络，当扰动加剧时将促使裂隙网络贯通巷道和上层含砂水层，水砂混合流将通过裂隙大量涌入生产工作面，形成突水溃砂灾害，带来巨大的经济损失和人员伤亡。 由于西部矿区地表存在风积砂，若扰动加剧上层含砂水层形成与地表的贯通裂隙，将有源源不断的砂供给，进一步加剧突水溃砂的灾害性。 为明确突水溃砂的成灾原因及危害程度，重点研究图1 中红圈位置水砂混合流在突发裂隙开口情况下的运移情况。 将实际突水溃砂时含砂水层中水砂进入破裂岩体这一情况简化为恒定压力下的单裂隙开口通道水砂运移数值计算模型如图2 所示。

图1 西部矿区突水溃砂示意Fig.1 Schematic of water and sand inrush in western mining area

图2 突水溃砂简化计算模型Fig.2 Simplified analysis model of water and send inrush

矩形通道中宽度为d的喉道口表征突水溃砂发生时突然增大的裂隙开口，边界压力P表征地下含砂水层中的水力压力情况。 水分布在开口上方的矩形区域，密度为ρw、动力黏度为υ。 砂粒用半径为r、密度为ρs、厚度为h、数量为N的球形颗粒群表征。 由于砂粒分布区域固定，且分析时以自然堆积方式排布，砂层厚度和砂粒数量呈正比，仅取1 项作为变量即可。 以P、d、h作为变量，从数值模拟角度分析水砂混合流在单裂隙下的运移规律。

2 LBM-DEM 耦合方法及模拟方案

LBM-DEM 耦合方法在模拟中对颗粒进行直接建模，颗粒拥有物理边界和确切的体积，流体假定为连续相并构建小于流场中最小涡长尺寸的网格进行直接数值模拟。 随着越来越多的学者不断完善基于LBM-DEM 方法下的液固耦合理论，此方法能够很好的分析液固耦合时颗粒流动和流场分布情况，并开始广泛应用于生物、医疗等多领域中［25］。

2.1 格子Boltzmann 方法（LBM）

格子Boltzmann 方法是应用非连续介质思想求解流体力学问题的方法。 其基本思想是把流体看成由许多只有质量没有体积的微小粒子组成，在时间、空间上离散，按照符合特定基本物理规律的演化规则碰撞，并沿网格线在节点之间迁移，利用分布函数的统计平均得到系统的宏观物理参数［26］。

借助于离散的单松弛时间格子Boltzmann -BGK 方程描述流体相互作用，即

其中；x为粒子空间位置矢量；ci为粒子速度矢量；t为时间；δt为时间步长；fi x，t( ) 为粒子分布函数；Fi x，t( ) 为离散的外力项；Ωi为离散的碰撞算子，可表达式为

其中：τc为2 次碰撞间隔时间；u为流体宏观速度矢量；fi，equ，ρ( ) 为离散后的平衡态速度分布函数，表达式为

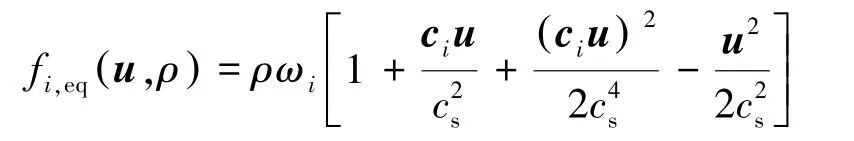
其中：ωi为权重系数；cs为格子声速，表达式为

式中：R为气体常数；T为热力学温度；D为空间维数。

考虑到实际应用，选取单松弛时间的D3Q19（3是空间维数，19 是离散速度数）三维模型，如图3 所示。 并根据三维模型各点坐标表征ci，i＝0，1，2，…，18，指可能迁移方向数。

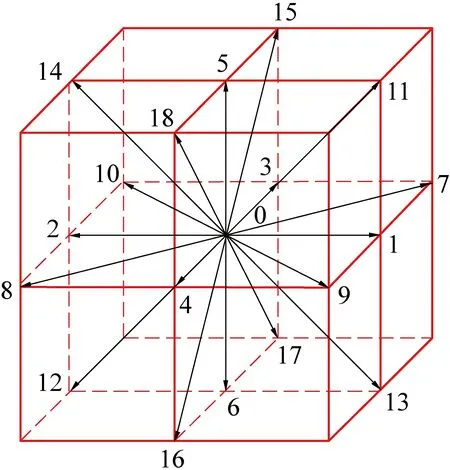
图3 D3Q19 模型Fig.3 D3Q19 model

若知道粒子分布函数，可计算模型的宏观密度、速度，其表达式为

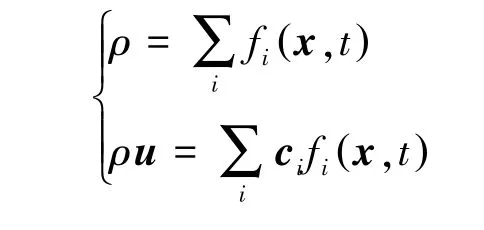
2.2 离散单元法（DEM）

离散单元法被广泛应用于岩石力学和颗粒流等离散系统模拟中，是基于非连续介质力学的数值方法［27］。 计算各个时间步上颗粒间所受的接触力及颗粒运动，分析时将运动分为平动和转动，平动在全局坐标系下计算，由牛顿方程给出，即

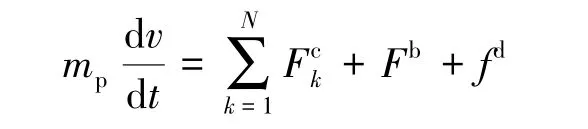
转动在局部坐标系下计算，需要计算出绕颗粒质心的合力矩，颗粒转动的控制方程为

式中：Ip为主惯性矩；ω为角速度；rk为颗粒上第k个接触处的矢径；Md为阻尼力矩。

2.3 浸入移动边界法（IMB）

浸入移动边界法是LBM 和DEM 的耦合方法，其具备碰撞算子的局部性和迁移操作的简单性，并在此基础上克服了传统耦合方法中的动量不连续性问题，具有足够代表性的网格非一致边界［28-30］。

所有离散的格子被分为纯流体格子、边界格子和纯固体格子3 类。 引入格子固含率εs定义每个格子内流固相互作用的影响，并通过格子内颗粒占据面积与格子占据总面积之比定量表征格子内流场和颗粒分布情况。 流体格子的固含率εs＝0，固体格子固含率εs＝1，边界格子的固含率εs为0～1，计算时用砂粒所占面积除以格子总面积，如图4 所示。

图4 格子分类示意Fig.4 Schematic of grid classification

为表征颗粒对流体的影响，在忽略外力项时将Boltzmann - BGK 方程添加源项变为

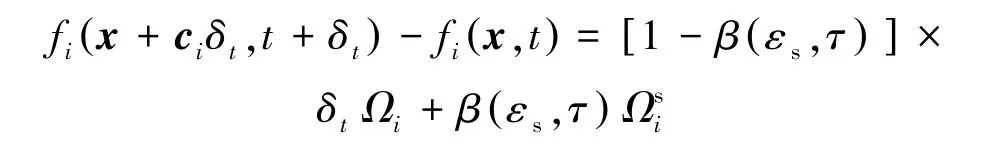
β（εs，τ） 是与格子固含率有关的附加碰撞项的加权函数。 表示为格子固含率εs和松弛因子τ的函数为

为考虑流体对颗粒的影响，通过加入所有被当前颗粒覆盖的格子上对颗粒的力和力矩表示周围流体作用于该颗粒的力和力矩，该力即颗粒受到的曳力，曳力F和力矩T的表达式分别为

其中，n为该颗粒覆盖边界格子的数目；m为离散速度数；xj为第j个边界格子的位置；xc为颗粒中心位置。 根据受力和力矩，颗粒对位置进行更新，其颗粒平动速度和转动角速度的更新式为

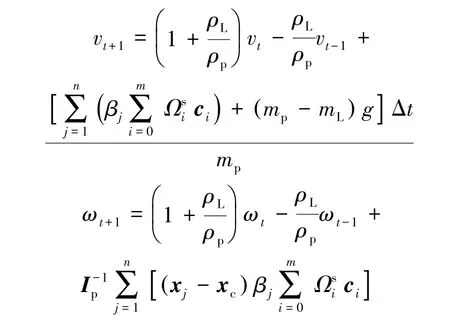
式中：ρL为流体密度；ρp为颗粒密度；mL为流体质量；g为重力加速度；Δt为计算时间步长。 最终通过颗粒和流体作用方程的不断迭代计算，实现水砂混合流的液固耦合计算。

2.4 计算流程

基于LBM-DEM 实现了水砂混合流的液固耦合，大量学者已通过对比单颗粒沉降及两颗粒DKT（追击、接触、翻转）试验过程验证LBM-DEM 耦合方法的合理性，可用于进行水砂混合流的液固耦合计算［31］。 其计算流程为在初始t0时刻输入流场和颗粒信息，判断各格点上的格子固含率。 通过LBM计算下一时刻t1时流场信息，并根据DEM 循环计算颗粒上的碰撞，将其信息更新为t1时刻。 依次对时间步循环，直至判定精度达到要求结束计算，实现水砂混合流的液固耦合计算过程如图5 所示。

2.5 模型构建及模拟方案

考虑到实际突水溃砂问题，构建单裂隙通道三维数值计算模型如图6 所示。

图5 LBM-DEM 耦合计算过程Fig.5 Calculation process of LBM-DEM

图6 单裂隙通道三维数值计算模型Fig.6 Three-dimensional numerical model of single fracture passage

以裂隙开口档板最左侧为O 点、建立YOZ 坐标系，三维空间尺寸为0.015 m×0.400 m×0.600 m（X×Y×Z），水流区域和初始砂粒区域均位于裂隙开口上方，上下两面作用恒定压力驱使水流流动，砂粒计算前先进行自由堆积，再通过坐标导入计算模型，使其均匀分布在开口上方。 模型参数设置：ρw＝1 000 kg/m3；υ＝0.001 Pa·s；ρs＝2 500 kg/m3；r＝0.002 m；E＝4.9 GPa。

为探究突水溃砂成灾的主导因素，改变不同边界压力P、裂隙开口宽度d和砂层厚度h分析水砂混合流在模型中的流动情况，统计裂隙开口处截面流量及溃砂速率的变化，方案见表1。

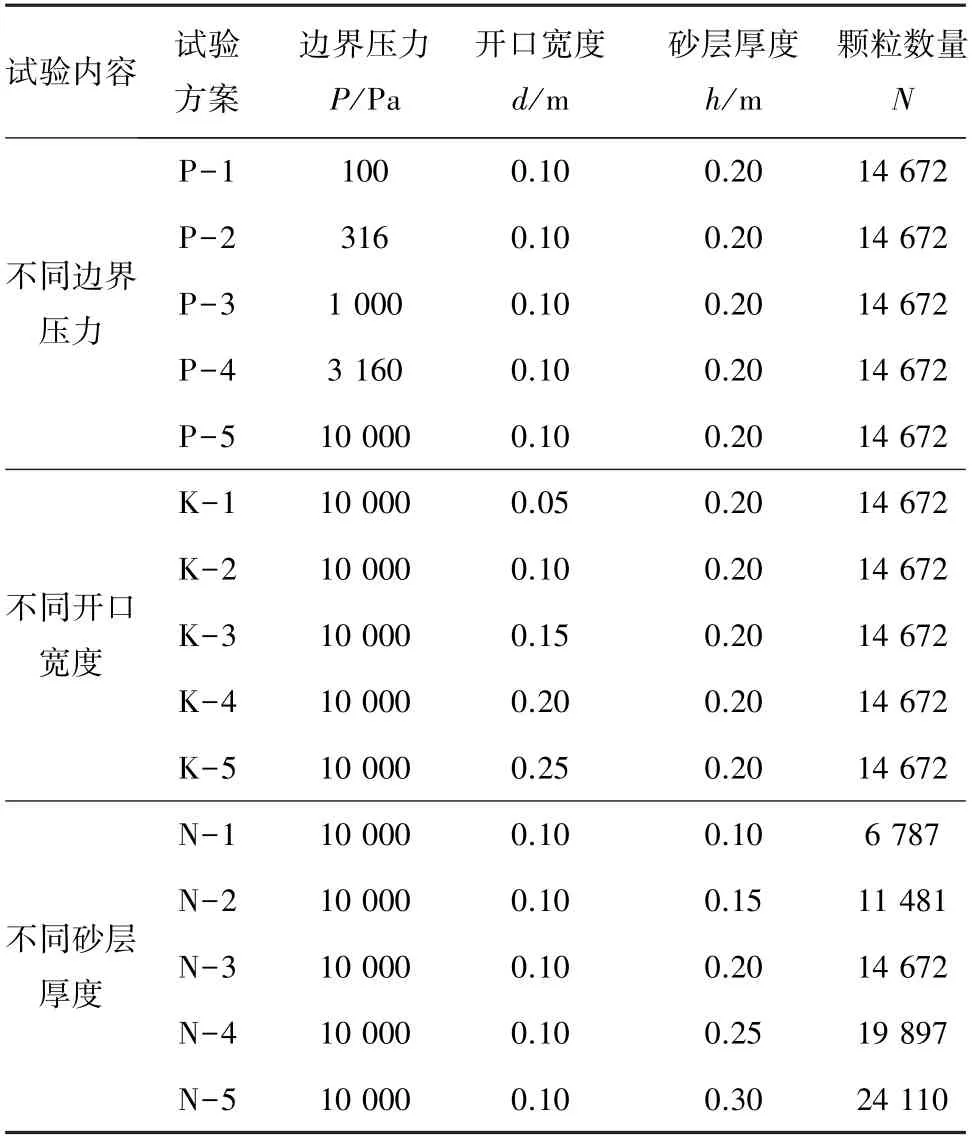
表1 模拟方案Table 1 Simulation schemes

3 计算结果分析

3.1 不同边界压力下水砂运移规律

模拟不同边界压力下水砂混合流的运移情况如图7 所示，随着边界压力的增加，溃砂量和裂隙开口处最大流速明显增加。 为定量研究溃砂增加量及流场变化，对裂隙开口处截面的流量Sw和单位时间溃砂速率vs与时间t关系进行分析（图8、图9）。

随着边界压力的增加，最终的稳定流量逐渐增加（图8）。 边界压力较小时流量先增加后保持恒定，而高压力时在达到早期稳定区持续一段时间后流量会再次升高，以P-5 最为明显。 对比图9 中溃砂速率变化可发现同样的规律，压力较小时溃砂速率先增至峰值后保持恒定，而随着压力的增加，溃砂速率从初始到峰值的增幅变大，但在峰值平台区持续的时间变短，之后出现明显降低，且随着压力增加降幅逐渐增大。 考虑到流量二次增加的时间点和溃砂速率从峰值开始降低的时间基本一致。 以P-5为例，分析了5 个等距时间步上截面流量、溃砂速率及溃砂形貌（图10），并通过红色虚线标记不同压力时颗粒中的主要受力区。

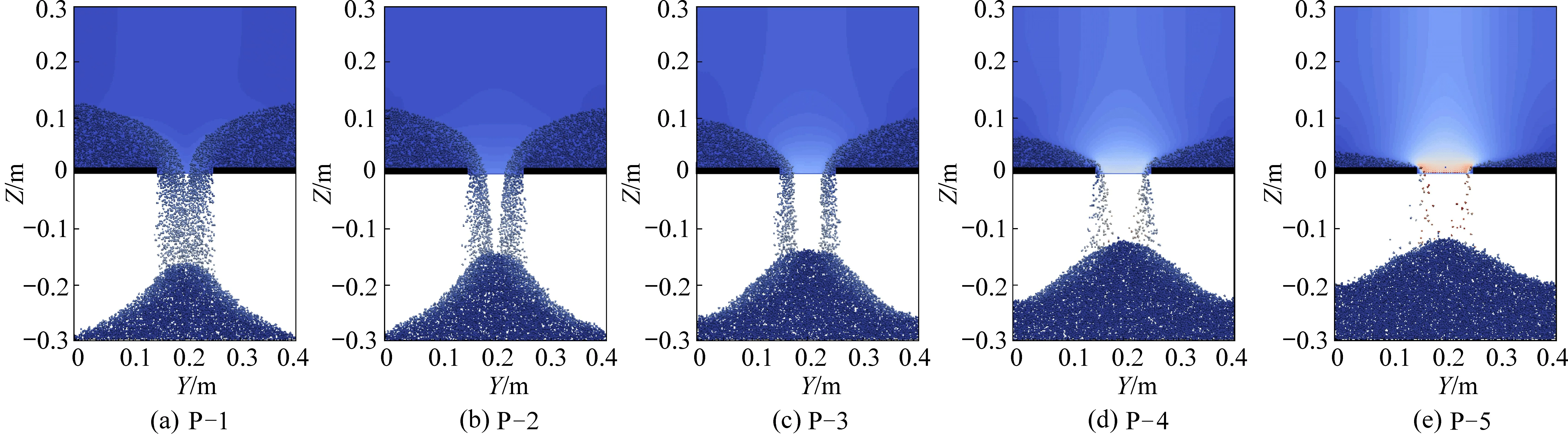
图7 不同边界压力下水砂运移Fig.7 Migration of sediment at different boundary pressures

图8 不同边界压力下截面流量变化Fig.8 Flow changes of cross section under different boundary pressures

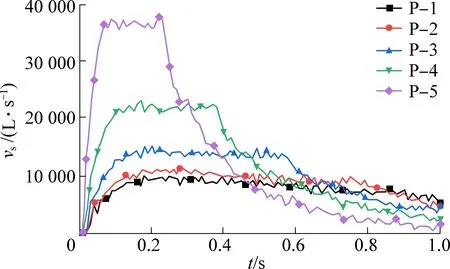
图9 不同边界压力下溃砂速率变化Fig.9 Changes of sand breaking rate underdifferent boundary pressures

从图10 所知，在①—③步中截面流量和溃砂速率基本不发生变化，此时在水流驱动作用下砂粒将在裂隙出口处形成临时的拱状受力结构，颗粒间相互作用使砂粒更加密集，对流场有一定的阻碍作用。随着砂粒的不断流出，出口处的拱状结构逐渐变化，其中心处不断凹陷。 至第④步时拱状结构变为类似“M”状结构，仍对水流及流砂有阻碍作用。 直至第⑤步时，中心砂粒完全流出喉道口，拱状结构完全消失后不再对流场起到阻碍作用，此时流量会快速上升，而由于砂粒已大量流出其溃砂速率会快速下降。

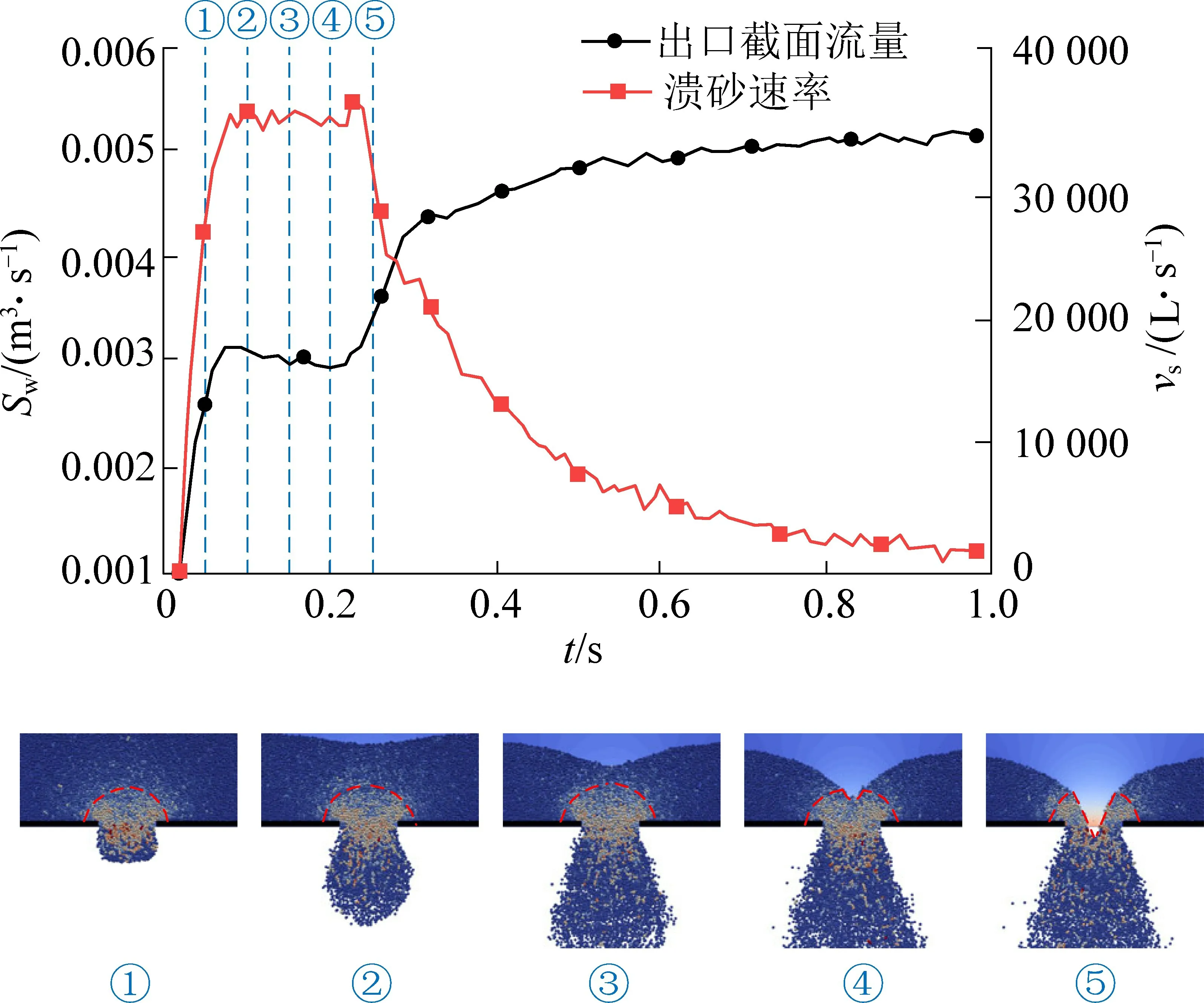
图10 P-5 截面流量和溃砂速率对比Fig.10 Comparison of cross section flow rate and sediment burst rate of Orifice P-5

为表征不同边界压力对水砂流动的影响程度，统计单位时间溃砂速率最大值及初始阶段受砂粒阻碍作用的平均流量随压力的变化规律如图11 所示。其中随着边界压力的增加，最大溃砂速率和平均流量均单调递增。 计算最大溃砂速率及初始平均孔口流量随压力的区间增幅，并通过区间增幅除以区间范围得出单位压力增幅以表征不同压力数值下的影响情况，计算结果见表2。

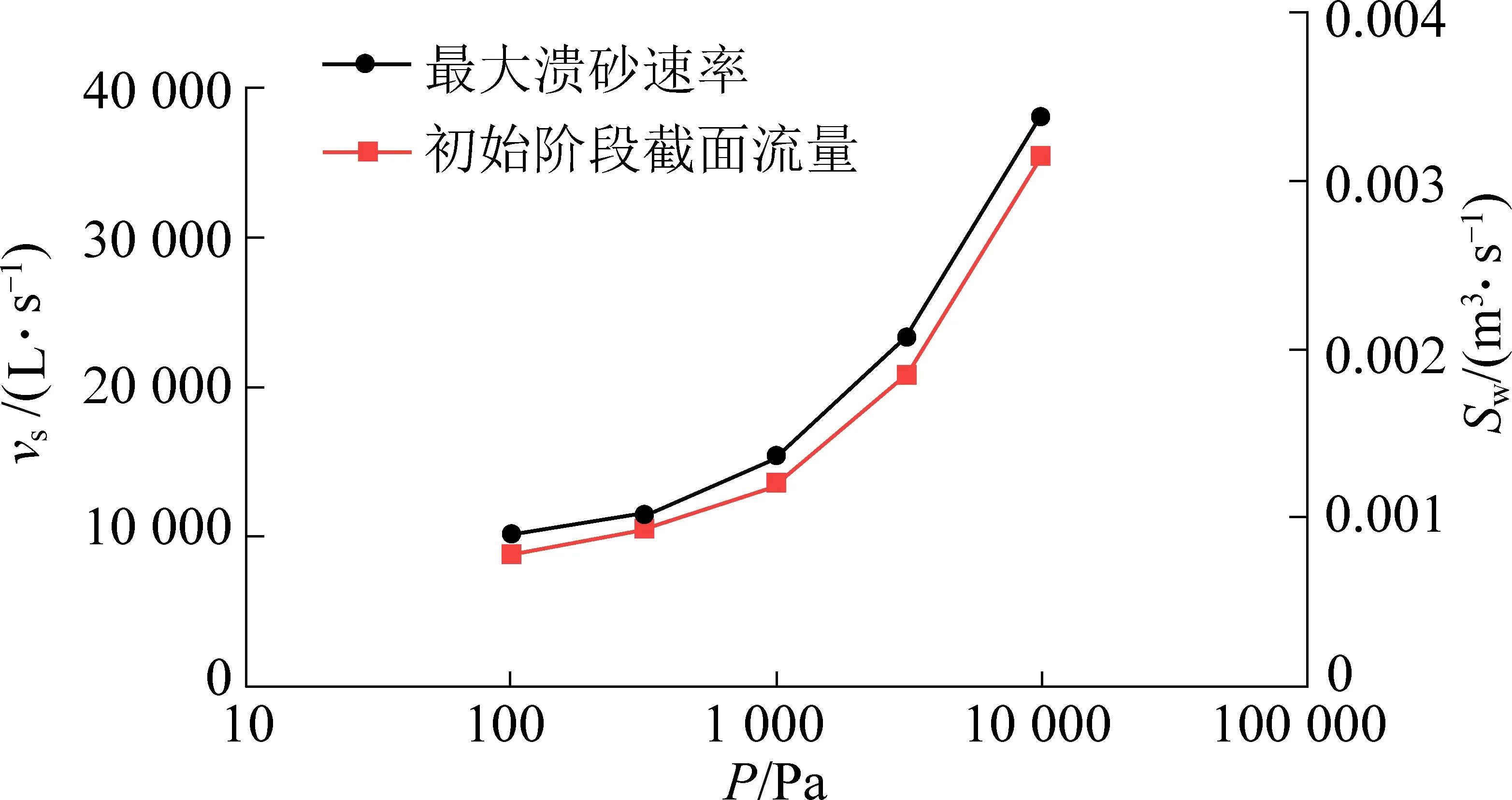
图11 截面流量和溃砂速率随边界压力变化Fig.11 Variations of cross section flow rate and sediment burst rate with boundary pressures

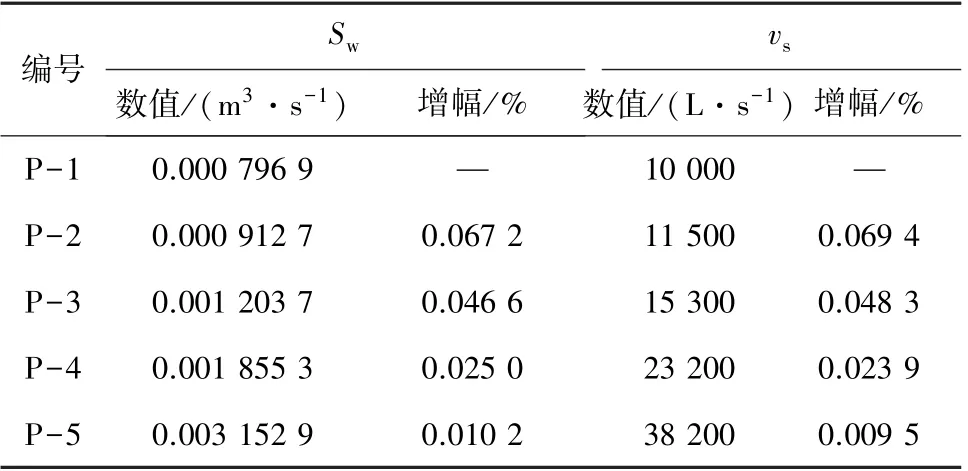
表2 截面流量和溃砂速率随边界压力的增幅Table 2 Increase of cross section flow rate and sediment burst rate with boundary pressure

从表3 发现，低压力时随压力的增加最大溃砂速率和平均流量的增幅均大于高压力时。 说明仅考虑边界压力情况下，随着边界压力的增加，同等时间下突水溃砂灾害程度会逐渐加剧，但低压力下由于压力增加引发的灾害加剧程度较大，此时应注意由压力增加引起的剧烈波动。 由于模型中设置恒定压差表征地下承压含水层作用，未考虑实际流动中压力降低的作用，结论仅能在一定程度上适用于工程实际问题，后续将针对复杂模型继续研究。

针对干砂单裂隙开口通道下流出孔口时单位质量流量计算，1961 年BEVERLOO 等［32］最早给出单位质量流量W的计算式为

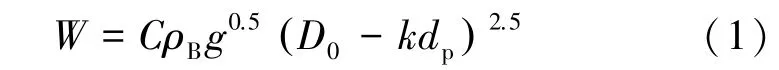
式中：C为与颗粒间摩擦性质相关的无因次量；ρB为颗粒堆积密度，通过颗粒密度ρs与空隙度ε计算，表示为ρB＝ρs1-ε( ) ；D0为孔口直径；dp为颗粒直径；k为无因次系数。

但式（1） 未考虑流体与颗粒并存情况，BULSARA 等［33］引入压力梯度概念得出含流体时颗粒流出孔口时单位质量流量计算式为

其中：P1和P2分别为孔板下方及上方压力。 郭帅等［34］通过试验分析验证了其合理性，模拟时设置不同恒定压差以驱动水流，参照式（2）给出最大溃砂量随压差的计算式为

其中：ΔP为模型恒定压差；W0为干砂在孔口的单位质量流量，能有效表征压差为零时干砂受自重下落的情况。 图12 给出式（3）拟合曲线与数值模拟数据点对比情况，曲线拟合情况较好。

图12 单位质量流量数据点与拟合曲线对比Fig.12 Comparison of data points per unit mass flow and fitting curve

3.2 不同开口宽度下水砂运移规律

模拟不同开口宽度下的水砂混合流运移情况表明：随开口宽度的增加，溃砂量及开口处最大流速明显增加，且流速高速区逐渐贯穿整个流场。 为明确溃砂增加量及流场变化情况，图13、图14 中结合裂隙开口处相同截面的流量Sw和单位时间溃砂速率vs进行分析。

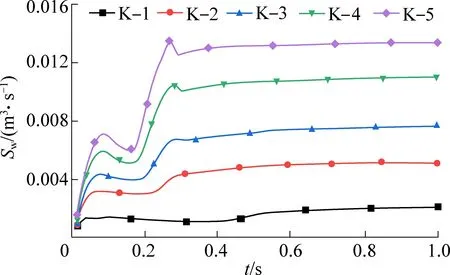
图13 不同开口宽度下截面流量变化Fig.13 Variation of flow rate of orifice section with different opening widths

随着开口宽度的增加，最终的稳定流量逐渐增加，如图13 所示。 开口较小时出口截面流量在达到初始流量峰值后保持恒定一段时间后再逐渐增加，开口较大时，达到初始流量峰值后将出现明显的下降阶段，之后又由于颗粒大量流出开口使流量逐渐增至最终稳定流量，以K-4、K-5 最为明显。

随着开口宽度的增加，溃砂速率从初始到峰值的增幅变大，且在峰值平台区持续的时间变短，如图14 所示。 开口宽度较小时溃砂速率增加到峰值将保持恒定一段时间，后由于砂粒逐渐流出裂隙出现缓慢降低。 开口宽度较大时，溃砂速率达到峰值保持一定时间后由于砂粒流出开口急速降低。 在开口进一步扩大后，甚至在峰值持续阶段出现一段小幅降低。

图14 不同开口宽度下溃砂速率变化Fig.14 Change of sediment discharge rate under different opening widths

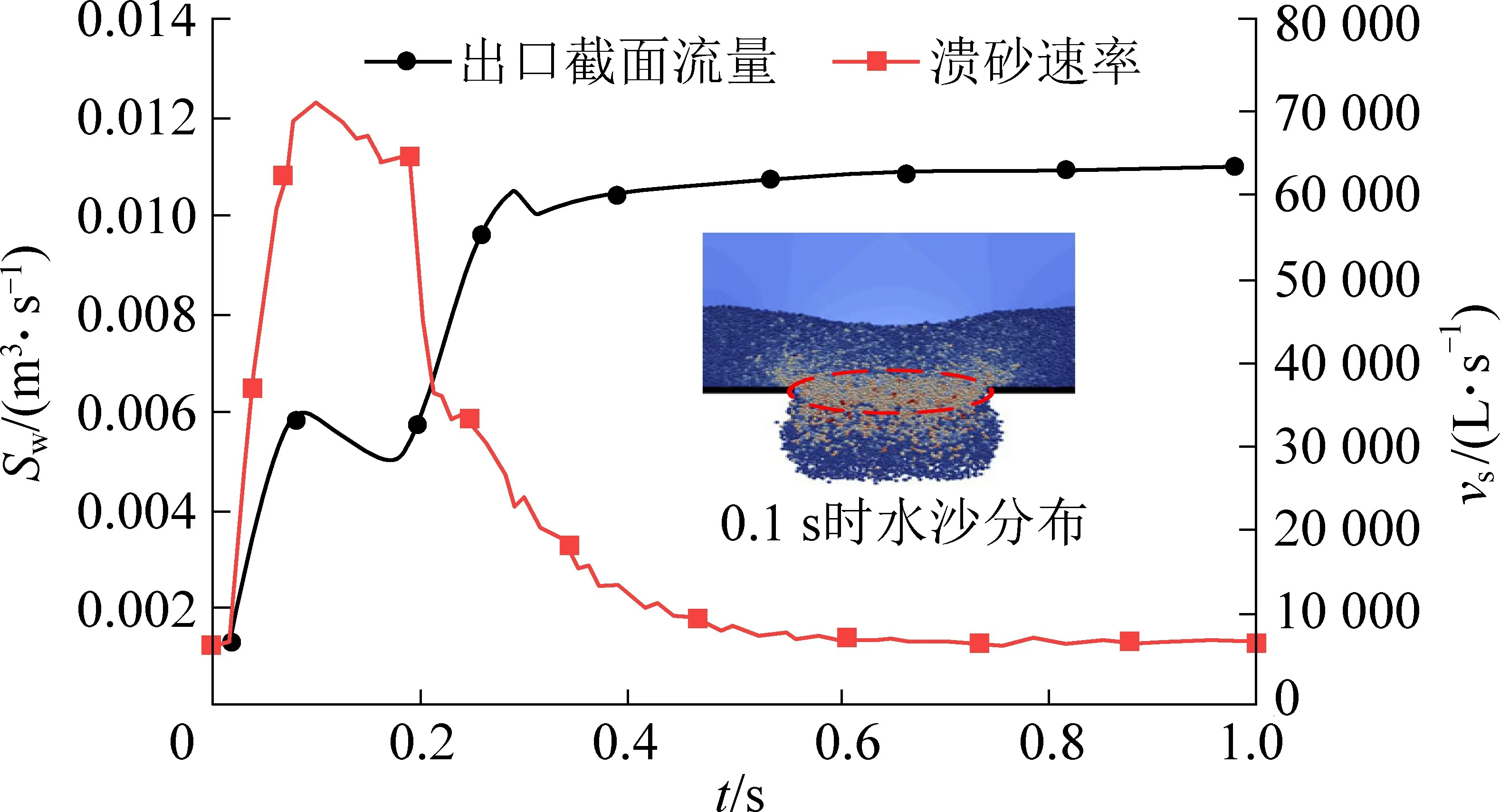
图15 K-4 截面流量和溃砂速率对比Fig.15 Comparison of cross section flow rate and sediment burst rate of K-4 orifice

因此，以K-4 为例，结合流量、溃砂速率、小幅降低时刻的水砂分布情况进行分析，并用红色虚线标示出大量砂粒受挤压聚集在开口处的现象，如图15 所示。 分析可知砂粒受挤压在开口处形成密实堆积结构影响水砂运移，造成溃砂速率和截面流量小幅下降，但由于结构中的砂粒具有流动性，形成的密实结构会随着砂粒流出开口逐渐失去其阻碍效果，直至砂粒中心平面降至孔口下方时该结构消失。

图16 中选取溃砂速率峰值时不同孔口下水砂分布形态进行分析，如图16 所示，以红色虚线画出不同开口上方的密实结构区域，随着开口宽度的增加，在孔口处形成的密实结构体积不断增加，对流场造成的影响程度将不断增大。 开口较小时，由于密实结构范围小，其受挤压砂粒相对总体砂粒占比较小，影响效果不明显。 开口较大时密实区范围较大，影响砂粒数量占比较多，将对整体水砂运移产生巨大影响。

图16 不同开口宽度下水砂运移Fig.16 Migration diagram of sediment with different opening widths

为表征不同开口宽度对水砂流动的影响程度，图17 中给出单位时间溃砂速率最大值及初始阶段受砂粒阻碍作用的平均流量随开口宽度的变化规律。

图17 截面流量和溃砂速率随开口宽度的变化Fig.17 Variation of cross section flow rate and sand breaking rate of orifice vary with opening width

随着边界压力的增加，最大溃砂速率和初始阶段平均流量均单调递增（图17）。 为量化开口宽度的影响，表3 给出最大溃砂速率和初始平均流量随开口宽度的区间增幅。

通过表3 发现，开口宽度较小时随宽度增加对最大溃砂速率和初始平均流量的影响大于开口宽度较大时。 说明固定的砂含量下，随着裂隙开口宽度的增加，突水溃砂灾害程度的增幅逐渐减小，在宽度大于一定值后，由于砂含量的限制灾害逐渐趋于恒定。 突增现象最容易出现在细小裂隙开口扩张的过程中。

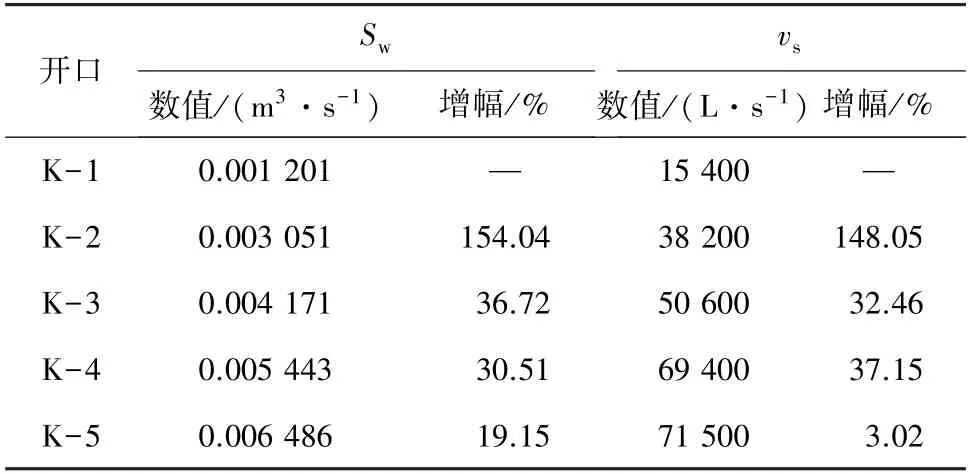
表3 截面流量和溃砂速率随开口宽度的增幅Table 3 Variation of cross section flow rate and sand breaking rate increase with width of opening

3.3 不同砂层厚度下水砂运移规律

密实填充下砂层厚度与砂粒数目呈正比，不同砂层厚度可表征不同砂粒数目对水砂运移的影响。模拟不同砂层厚度下水砂运移结果表明：随着砂层厚度的增加，砂粒数目增加，最终的溃砂量明显增加，且开口两侧堆积的未流出砂粒也逐渐增加，但流速未产生明显变化。 为明确溃砂增加量及流场变化情况，图18、图19 结合开口处的截面流量Sw和单位时间溃砂速率vs进行分析。

图18 不同砂层厚度下截面流量变化Fig.18 Variation of cross section flow of orifice with sand thickness

图19 不同砂层厚度下溃砂速率变化Fig.19 Changes of sediment discharge rate under different sand thickness

从图18 所知，最终稳定流量不随砂层厚度的增加发生变化。 而随着砂层厚度的增加，截面流量在达到初始峰值后均出现一定的下降，用对应曲线颜色的虚线记录最终时间，①表示初始流量峰值点，②③④⑤分别对应N-2、N-3、N-4、N-5 时最终下落结束的时间点，发现下降持续的时间随着砂层厚度的增加逐渐增长。 说明随着砂层厚度的增加，下落过程中对水流的阻碍作用越明显。

如图19 所示，随着砂层厚度的增加，溃砂速率峰值点位置不断延后。 在砂层厚度较大时，均呈现先急速增至初始高速率后持续降低一段时间，再升至峰值速率后快速下降的趋势。 同样用①表示初始速率峰值点，②③④⑤分别对应N-2、N-3、N-4、N-5 时速率持续下降结束的时间点，发现随着砂层厚度的增加，从初始高速率降至最小速率的持续时间不断增长，说明砂层厚度的增加对砂层整体溃突阻碍作用逐渐增加。 为分析砂层厚度较大时对水砂运移的阻碍形式，图20 以N-5 为例，结合流量、溃砂速率及不同时刻水砂分布情况进行分析。

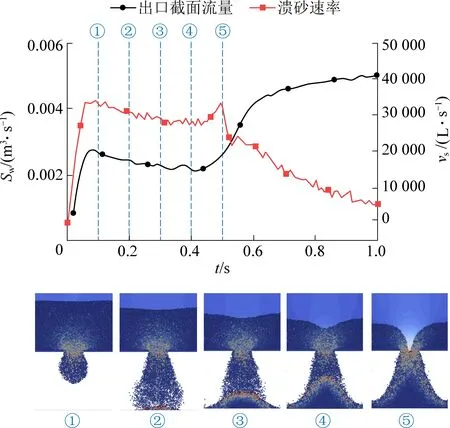
图20 N-5 截面流量和溃砂速率对比Fig.20 Comparison of cross section flow rate and sediment burst rate of Orifice N-5

从图20 可知，对水流及整体砂粒流速起阻碍作用的原因主要为砂粒在裂隙开口处聚集形成密实区域，对比各阶段可以发现①②③④时刻大量砂粒受力后聚集在裂隙开口，使得水砂流动减缓，在⑤时刻砂粒形成的密实结构崩塌，对流体的阻碍消失，截面流量逐渐开始上升。 而此时由于密实结构崩塌后大量砂粒倾泻将造成此时的溃砂速率达到峰值。 为明确不同砂层厚度对水砂运移的影响，图21 分析不同砂层高度下单位时间溃砂速率最大值及初始阶段受砂粒阻碍作用阶段平均流量的变化规律。

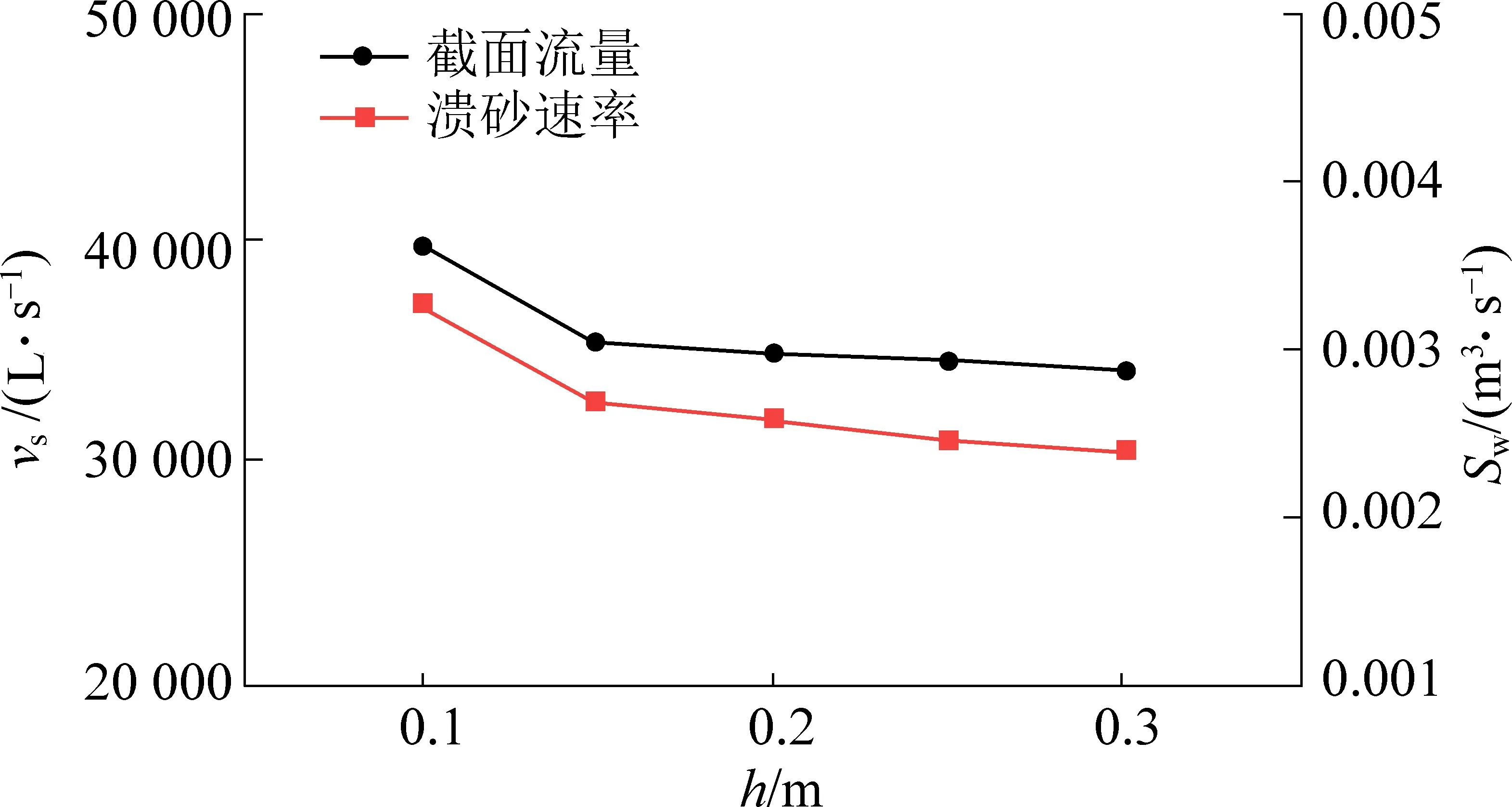
图21 截面流量和溃砂速率随砂层厚度的变化Fig.21 Variation of cross section flow rate of orifice and rate of sediment burst change with thickness of sand layer

随着砂层厚度的增加，最大溃砂速率和平均流量均单调递减（图21），在砂层厚度较小时出现均快速降低的现象。 当砂层厚度较大时，随砂层厚度增加对最大溃砂速率和平均流量的影响较小。 为定量研究砂层厚度对水砂运移的影响程度，表4 计算给出不同砂层厚度下最大溃砂速率和平均流量的区间降幅。

表4 截面流量和溃砂速率随砂层高度的降幅Table 4 Decrease of cross section flow rate and sediment burst rate with thickness of sand layer

由表5 知，在砂层厚度较小时随砂层厚度增加最大溃砂速率和平均流量的降幅远大于砂层厚度较大时，在N-2 时的降幅基本为N-5 时的10 倍。 说明在边界压力、砂层范围及裂隙开口恒定的情况下，随着砂层厚度的增加，包含的砂粒数量增多，同等时间下由于砂粒阻碍作用增强其突水溃砂灾害程度会逐渐减小。 当砂层厚度较小时，水驱动砂快速流出裂隙孔口，灾害最为严重。 而砂层越厚砂粒越容易在裂隙口拥堵阻碍砂粒及流体运动，此时在砂粒密实结构失稳造成砂粒倾泻时发生最严重的灾害。 分析仅考虑同等时间下的灾害影响，未研究不同砂层厚度砂粒全部流出情况，此情况明显为砂层厚度越大，可流出砂粒增加造成灾害愈加严重。

4 结论及展望

1）随边界压力增加，截面流量及最大溃砂速率均单调增加，同等时间下突水溃砂灾害程度会逐渐加剧。 由于高压力下砂粒更加容易在喉道口堆积成临时性密实结构阻碍水砂运移，升高单位压力时引起的最大溃砂量及平均截面流量的增幅逐渐降低。在Bulsara 式基础上考虑流体与颗粒并存情况下给出的计算式能较好地拟合最大单位质量流量曲线。

2）随开口宽度增加，截面流量及最大溃砂速率均单调增加，同等时间下突水溃砂灾害程度会逐渐加剧。 砂粒在开口处形成的密实结构体积逐渐增加单增速不断降低，截面流量及最大溃砂速率增幅逐渐降低，小开口时由宽度增加引发的灾害加剧大于大开口情况。 发现砂粒在开口处形成的密实结构体积增加速率对灾害程度起关键影响，细小裂隙开口扩张的过程中更易出现水砂流速突增，诱发突水溃砂灾害。

3）随砂层厚度增加，截面流量及最大溃砂速率均单调减少，且降幅在小厚度时达最大后逐级减小至趋于平稳，小厚度区间降幅可达大厚度的10 倍，在开口处形成的砂粒密实结构持续时间增长，对水砂运移的阻碍效果逐渐增加，同等时间下突水溃砂灾害程度会逐渐减弱。 不同厚度下灾害特点不同，厚度较小时，灾害发生在水驱动砂快速流出裂隙孔口阶段，厚度较大时，灾害发生在砂粒密实结构失稳造成砂粒倾泻阶段。

实际突水溃砂问题不仅需要考虑裂隙开口处的水砂流动问题，还需要分析在裂隙网络中的流动及对裂隙网络的侵蚀等相关问题。 后续将针对平面裂隙网络中的流动问题、空间破裂岩体通道中的流动问题及裂隙通道中的渗流侵蚀问题进行研究，为突水溃砂灾害防控提供理论指导。