压电加速度传感器Hn估计校准方法

金 冉，陈 伟，刘国富，王春羽，蒲 红

（贵州航天计量测试技术研究所，贵阳550009）

加速度传感器是航空航天领域进行结构模态分析和振动环境试验必不可少的设备，压电加速度传感器由于其频响性能优良而被广泛应用。压电加速度传感器的灵敏度频响性能是测量或试验结果准确的关键，故对其灵敏度幅频特性进行校准具有重要的意义。

针对其灵敏度幅频特性的校准，行业内普遍采用的方法为正弦逐点校准，也称“单频校准”[1-2]。传感器校准过程中，影响校准结果准确度的主要因素包括两方面，一方面是传感器安装不同轴、工装刚度低和分析仪通道性能不一致等因素引入的系统误差；另一方面是激振信号叠加或A/D采样过程混入噪声信号，导致结果引入随机误差[1-2]。目前，一般采用“替代法”减小系统误差，通过大量实践证明，其效果显著。在降低系统噪声影响方面，硬件上采用信噪比较高的激振器和数据采集仪，软件方面计算过程中一般应用H1估计法或H2估计法进一步抑制噪声，可提高测量结果的准确度[3-7]。

由于H1估计不能消除输入噪声的影响，H2估计不能消除输出噪声的影响，故当系统中的噪声变大时，H1估计法或H2估计法的噪声抑制效果不明显。滑广军等提出Hn估计[8-9]方法，可在采样数据等长度情况下，使功率谱估计次数变为N(N-1)/2次，可较大程度减小噪声对测量结果的影响，该方法主要应用在结构模态分析方面，但在压电加速度传感器校准方面的应用，尚未见文献报道。

功率谱估计是Hn估计法必不可少的步骤，用间接法计算功率谱时，应首先计算相关函数，根据定义对有限长度的采样数据进行计算时，相当于给连续函数加三角窗，最终的结果为有偏估计；若采用式(1)计算相关函数：

即在相关函数初始段截取较少的点进行计算，则造成存储空间的浪费；或者采用式(2)对相关函数进行加权处理，可实现功率谱的无偏估计，但对于固定的N值，随着|m|的增大，其方差性能变坏[10]。

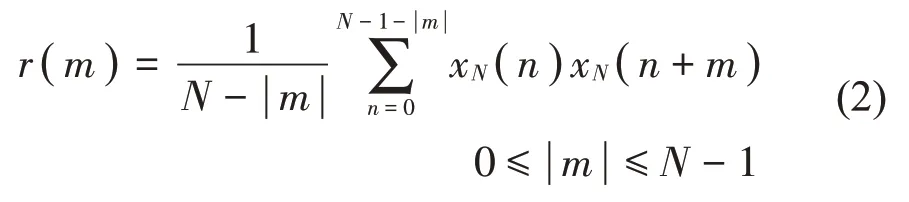
基于以上分析，本文提出一种改进的压电加速度计校准方法：首先用“替代法”激励传感器并进行信号采集；再基于Hn估计原理，对采样信号进行分组，并用半长法对不同组的采样数据进行互相关计算；最后求其互功率谱，计算频响函数，实现对信号中噪声抑制，增加测量结果的准确度。

1 压电加速度传感器校准系统及其频响函数

采用比较法校准加速度传感器时，用“背靠背”方式进行安装，压电加速度传感器校准系统的原理图如图1所示。

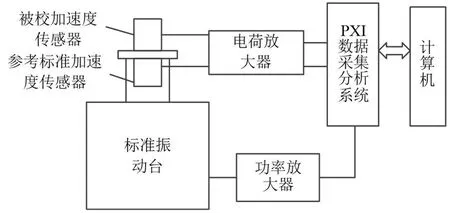
图1 压电加速度传感器校准系统原理图

采用比较法校准时，计算机控制动态信号分析仪（PXI数据采集分析系统）输出对应频率的正弦信号，功率放大器对正弦信号进行放大，驱动标准振动台产生标准振动激励，参考标准加速度传感器与被校加速度传感器的输出信号由电荷放大器进行转换、滤波处理，PXI数据采集系统对输入的传感器信号进行采样并发送到计算机，计算机对离散采样信号进行计算，得到被校加速度传感器的灵敏度。压电加速度传感器校准系统的模型如图2所示。

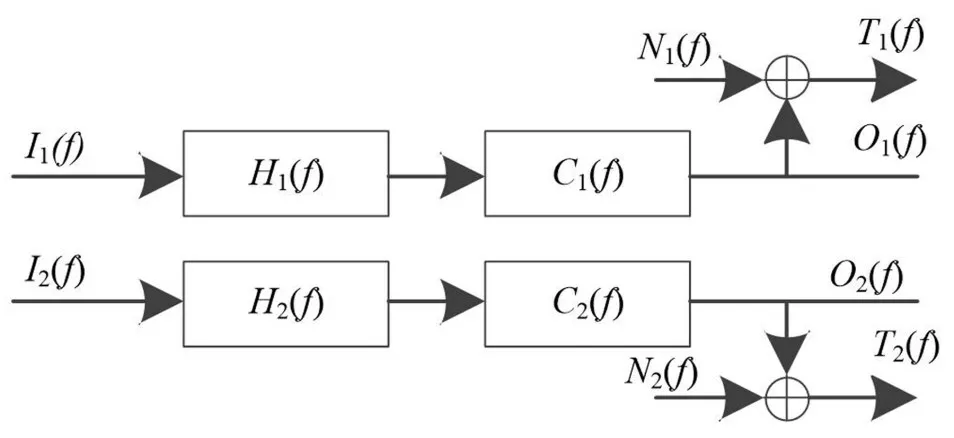
图2 传感器校准系统模型

图2中，I1(f)、I2(f)分别为参考标准加速度传感器和被校加速度传感器输出信号的频域表示；O1(f)、O2(f)分别为无噪声影响时参考标准加速度传感器和被校加速度感器所采集的并经电荷放大器与PXI数据采集系统处理后得到的信号（以下称“两组测得信号”）的频域表示；T1(f)、T2(f)分别为所测得两组信号的频域表示；N1(f)、N2(f)分别为这两组信号中引入的噪声信号的频域表示；H1(f)、H2(f)分别为电荷放大器两通道的频率响应响函数；C1(f)、C2(f)分别为PXI数据采集分析仪两通道的频率响应函数。

用比较法校准，校准结果同时受到系统误差和随机误差的影响，用替代法校准可减小误差，替代法校准的安装示意图如图3所示。

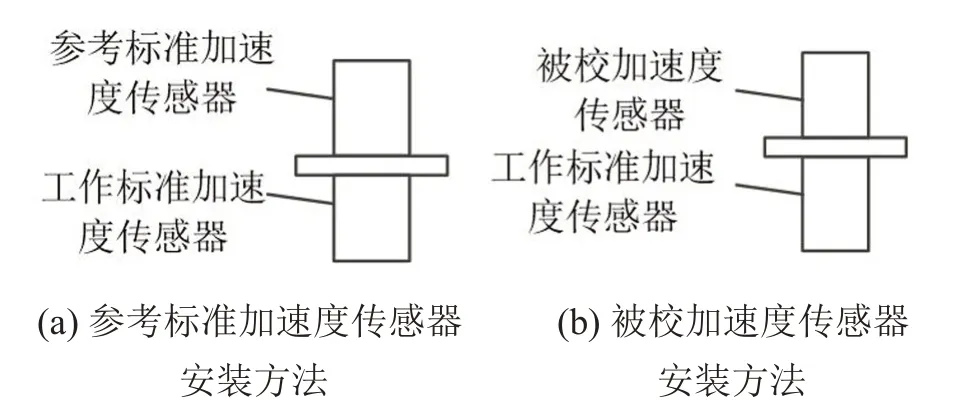
图3 替代法校准安装示意图

参考图3，先用工作标准加速度传感器替代参考标准加速度传感器、参考标准加速度传感器替代被校加速度传感器，测量并存储工作标准加速度传感器和参考标准加速度传感器之间的传递函数Hr/z(f)，不考虑噪声的影响：

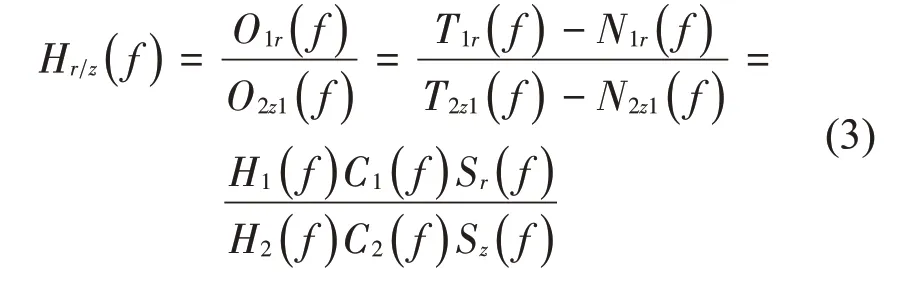
再安装被校加速度传感器，测量并存储被校传感器和工作标准加速度传感器之间的传递函数Hu/z(f)，不考虑噪声的影响：

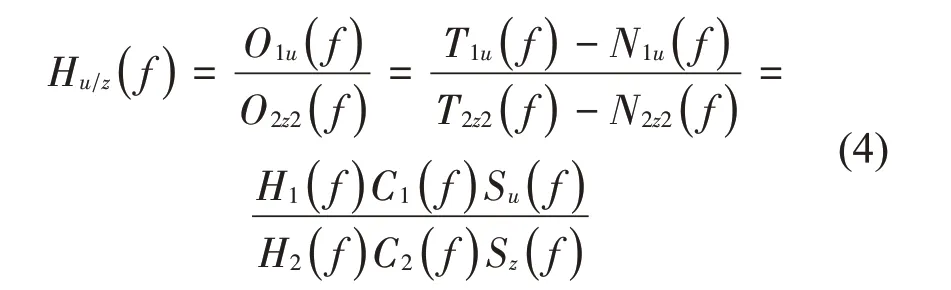
将式(1)除以式(2)，并进行整理，得：

由式(3)至式(5)可知，替代法可消除由通道不一致引起的系统误差，系统噪声成为影响校准结果准确度的主要因素。

2 Hn估计方法原理

以工作压电加速度传感器的灵敏度计算为例进行说明。同时对含有加性噪声的参考加速度传感器和工作加速度传感器输出信号进行N(N≥2)次采样，单次采样时关系式(6)成立。

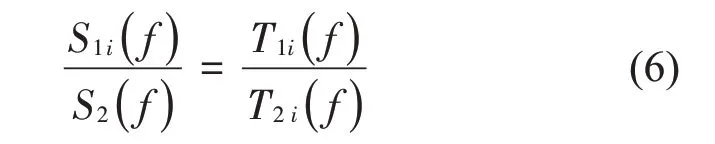
式中：T1i(f)、T2i(f)分别为第i组工作加速度传感器和参考加速度传感器输出采样数据的离散傅里叶变换；S1i(f)为工作加速度度感器的第i组灵敏度频响函数，S2(f)为参考标准加速度传感器的灵敏度函数。

将分子与分母同时乘以T2j(f)(j=i+1，i+2，…，N)的共轭再求比值，得到：

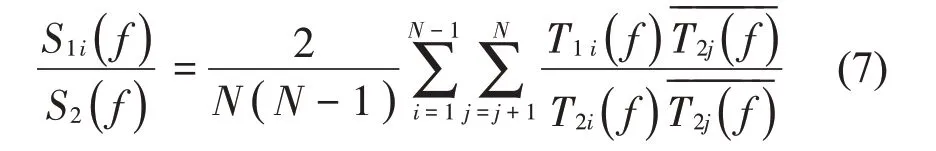
式中：

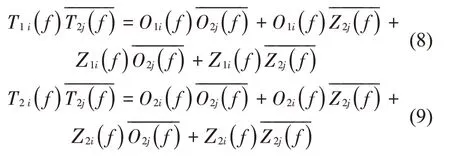
由于噪声信号的各态历经性，故不同时刻噪声信号的互功率谱、噪声信号与系统输出信号的互功率谱为零，故有：

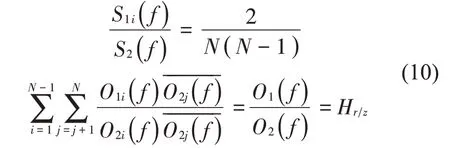
即

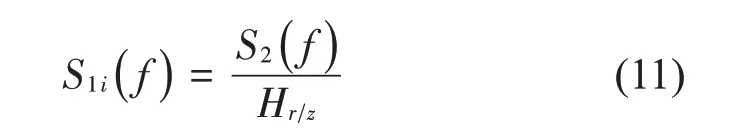
由式(10)和式(11)可见，应用上述Hn估计方法，可使S1i(f)的计算结果不受噪声的影响。同理，结合式(5)，可计算出Su(f)，其计算结果不受噪声的影响。

3 功率谱计算方法

由式(7)至式(10)可知，互功率谱的计算是整个计算过程中必不可少的环节。根据维纳-辛钦定理，宽平稳随机信号的功率谱密度是其自相关函数的傅里叶变换。本文运用“半长法”计算正弦信号的相关函数，再运用FFT 计算其功率谱。采用“半长法”计算互功率谱，设从同一正弦信号的不同时刻获得的两段离散采样序列为x(n)、y(n)，采样序列的采样频率相同且长度均为M，其自相关函数的计算公式为

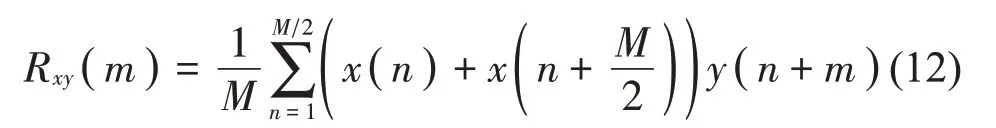
式中：m=0，2，…，M/2-1。从式(12)可知，计算相关函数时，取x(n)的一半，在y(n)上做滑动计算，计算单点Rxy(m)时所用的乘法次数均为M/2，加法次数均为M/2-1，计算结果为无偏估计。

对幅值为5的正弦信号，加信噪比为10 dB的高斯白噪声，将加噪信号进行离散化并截取10 000个离散数据，并将其分为10组，用“半长法”计算其中任意两组离散数据的相关函数，计算结果的波形如图4所示。

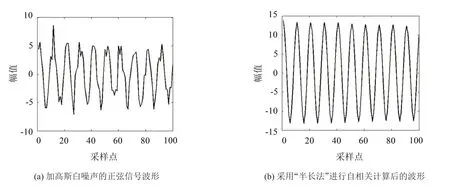
图4 基于“半长法”计算加噪正弦信号的自相关函数波形

从图中可知，根据“半长法”得到的自相关函数波形平滑且无衰减，达到了抑制噪声的目的，同时保证了波形的完整性，便于对其进行功率谱分析。

用上述10组离散数据计算仿真信号的功率谱密度。方法1：先直接对每组数据进行FFT 计算，再对计算结果进行平方运算；方法2：先采用式(2)计算每组数据的自相关函数，再对离散结果进行FFT 计算；方法3：先采用“半长法”计算每组信号的自相关函数，再对离散结果进行FFT 计算。分别计算根据上述3种方法求得的10组功率谱结果的方差，结果如表1所示。

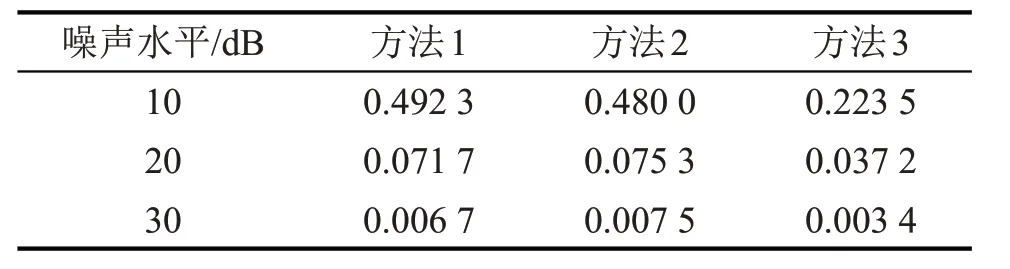
表1 根据3种方法计算的功率谱的方差

从表1可知，在不同噪声水平下，根据“半长法”计算得到的互功率谱结果的方差较小，约为前两种方法的50%，说明“半长法”抑制平稳信号的噪声效果良好。

4 改进校准方法的实现步骤

Hn估计利用噪声的互功率谱为零的性质，通过对多组数据求互功率谱，再计算其算术平均值，可有效地抑制噪声对计算结果的影响，提高加速度传感器校准结果的准确度。实现基于Hn估计的改进压电加速度传感器校准方法的具体步骤为：

（1）数据采集并分组。对工作标准压电加速度传感器和参考标准压电加速度传感器的输出信号进行数据采集，并进行分组，保持组数和单组数据长度相同，分别记为tri(m)、tui(m)(i=1，2，…，L；m=1，2，…M)；

（2）相关函数计算。对L组tri(m)和tui(m)进行互相关计算并求算术平均值，再对L组tui(m)求互相关计算并求平均值，计算公式为

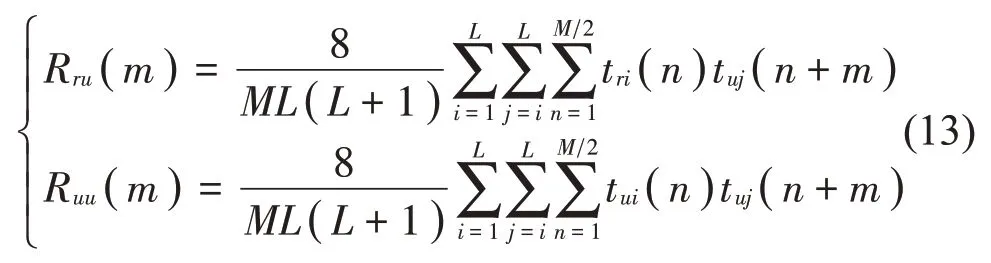
（3）功率谱计算。对相关函数进行FFT 分析，计算出L(L+1)/2组工作标准压电加速度传感器和参考标准压电加速度传感器的输出信号在对应频率点的功率谱密度；

（4）工作标准加速度传感器灵敏度计算。根据式(6)，计算L(L+1)/2组工作标准压电加速度传感器的灵敏度，并求算术平均值；

（5）改变激振频率，重复步骤（1）到步骤（4），并对工作标准压电加速度传感器在不同频率点处的灵敏度值进行存储；

（6）用被校压电加速度传感器替换参考标准压电加速度传感器，在相同条件下进行激振，并对传感器的输出信号进行处理，数据采集、相关函数计算、功率谱计、被校加速度传感器灵敏度计算等参照步骤（2）到步骤（4）进行。

首次校准时，先执行步骤（1）到步骤（4），用参考标准压电加速度传感器对工作标准压电加速度传感器的灵敏度进行校准并存储，后续校准时，若系统的状态未发生改变，可直接执行步骤（5）到步骤（8），使用测得的工作标准压电加速度传感器的灵敏度对被校压电加速度传感器的灵敏度频响函数进行校准。

5 实验分析

为了验证本文算法的准确性与实用性，设计实验计算被校压电加速度传感器的灵敏度，并计算其标准差。搭建的实验系统中，传感器部分包括两个8305型传感器和一个4368型传感器，配套2692型电荷放大器；振动激励装置包括4809型激振器和2706型功率放大器；信号发生器为33220A型函数发生器，数据采集分析仪由1065型PXIe 机箱和4497型高速数据采集板卡组成。由Labview软件产生加有白噪声的正弦离散数据，由控制函数发生器产生激励信号，通过功率放大器驱动激振器产生振动激励。搭建的校准实验系统如图5所示。校准过程中，两个8305型传感器与被校4368型传感器安装方法如图6所示。

以两个8305型压电加速度传感器中的一个作为工作标准压电加速度传感器，另一个作为参考标准压电加速度传感器，以4368型压电加速度传感器作为被校压电加速度传感器，分别以加入信噪比3 dB 和10 dB 高斯白噪声的正弦信号为激励信号，信号的主频率分别为5 Hz、20 Hz、80 Hz、160 Hz、315 Hz、630 Hz、1 280 Hz和2 000 Hz，在上述8个频率正弦激励条件下，按照替代法的操作步骤，用H1估计法、H2估计法和Hn估计法分别测量4368型压电加速度传感器的灵敏度，进行10次测量并计算平均值，计算结果如表2所示。

图5 校准实验系统

图6 传感器安装图

表2中，S对应的灵敏度值为在中频标准振动系统上测量得到的结果；S-3H1、S-3H2和S-3Hn分别为3 dB信噪比条件下根据H1估计法、H2估计法和Hn估计法计算得到的灵敏度值；S-10H1、S-10H2和S-10Hn分别为10 dB 信噪比条件下根据H1估计法、H2估计法和Hn估计法计算得到的灵敏度值。

以将在标准振动台上测量所得的10组数据进行平均得到的结果为真实值，以3 dB噪声条件下和10 dB 噪声条件下根据Hn估计法、H1估计法和H2估计法进行10次计算所得结果的平均值为实测值，求相对误差，相对误差的绝对值如图7所示。

分别计算在3 dB噪声条件下和10 dB噪声条件下根据Hn估计法、H1估计法和H2估计法进行10次计算所得结果的标准差，计算结果如图8所示。

由图7可知，在同一噪声水平下，在对应频率点处，基于Hn估计法所得计算结果的相对误差绝对值整体上比基于H1估计法和H2估计法所得结果小；结合图8可知，在同一噪声水平下，基于Hn估计法计算结果的标准差约为基于H1估计法和H2估计法计算结果的标准差的1/10，即在单次测量条件下，Hn估计Hn估计、H1估计和H2估计所得结果的相对误差法对噪声的抑制效果较H1估计法和H2估计法好。计算结果证明了本文计算方法的有效性。

图7 在各噪声条件下根据

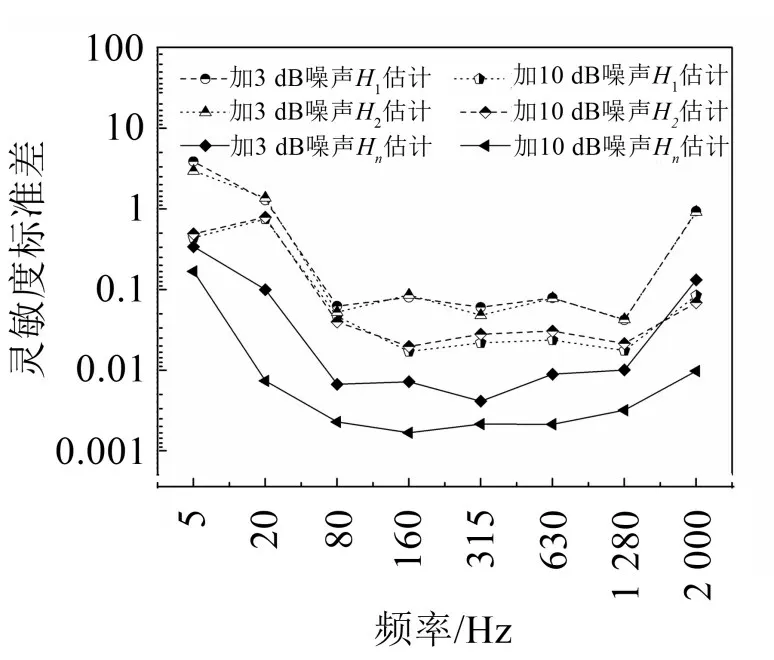
图8 在各噪声条件下根据Hn估计、H1估计和H2估计结果所得的标准差

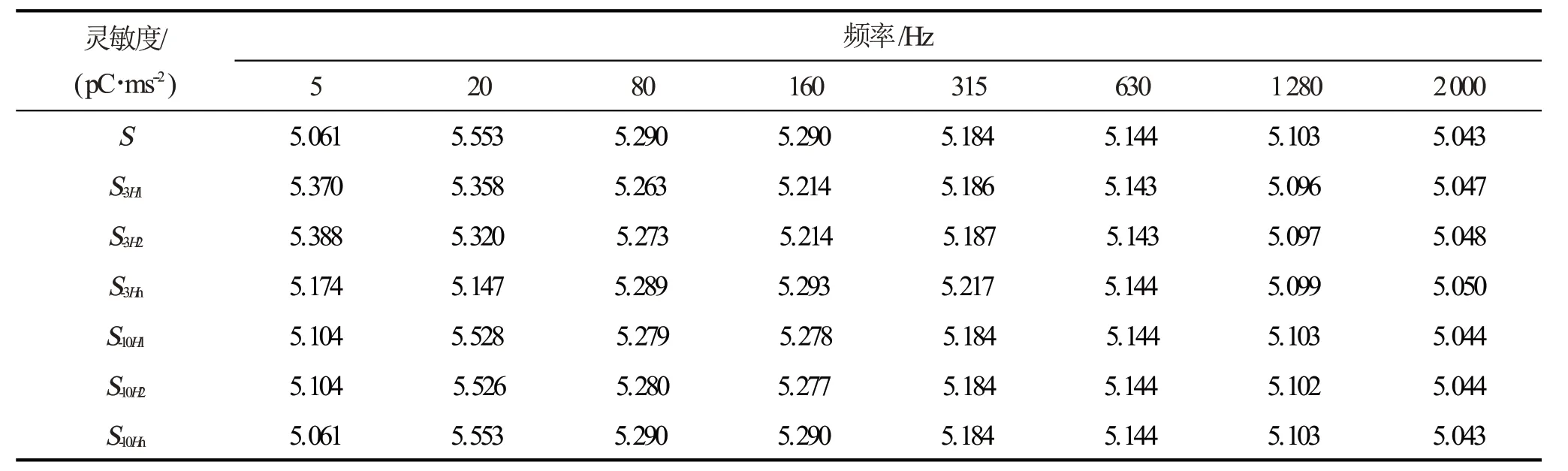
表2 不同噪声水平下被校压电加速度传感器的灵敏度

6 结语

本文提出了一种压电加速度传感器改进校准方法，并进行了实验验证，结果证明，相较H1估计方法和H2估计方法，噪声对根据该方法所得计算结果的影响更小，它提高了压电加速度传感器校准结果的准确度。在分析替代法校准中噪声对计算结果影响的基础上，介绍了Hn估计方法抑制信号噪声的原理、利用“半长法”计算相关函数以及功率谱的实现步骤，最后对算法进行仿真实验对比，仿真和实验结果证明了所提算法的有效性。