地铁车辆-轨道耦合振动响应分析及轨道结构参数优化
2021-04-17夏志强朱林军吴福来宋宏波施可南方火浪
夏志强,朱林军,吴福来,宋宏波,施可南,方火浪
(1.中国电建集团华东勘测设计研究院有限公司,杭州311122;2.杭州未来科技城建设有限公司,杭州310012;3.浙江大学 建筑工程学院,杭州310058)
随着我国城市轨道交通事业的发展,由地铁运行产生的振动和噪声对环境的影响越来越受到人们的重视。为了降低地铁运行对周围环境的影响,轨道多采用无砟轨道结构形式,如整体道床、板式道床、浮置板式道床等轨道结构。浮置板式无砟轨道在减振降噪方面效果明显,适用于人口密集的区域和一些特殊地区,钢弹簧浮置板轨道已在我国得到大量运用。目前已有许多学者对无砟轨道的动力学特性进行了研究分析。郭亚娟等[1]、侯德军等[2]、蒋崇达和雷晓燕[3]、李林峰等[4]和王少林等[5]建立了车辆-钢弹簧浮置板轨道耦合动力学模型,通过瞬态分析模拟了列车移动荷载经过钢弹簧浮置板轨道时的动力响应。金浩和刘维宁[6]探讨了梯式轨道枕下减振垫铺设方式对其减振能力的影响,根据实际应用和试验经验,提出了两种全新的枕下减振垫铺设方式。余关仁等[7]和王小韬等[8]研究了扣件和钢弹簧隔振器失效对轨道动力响应的影响。陈林和姚林泉[9]建立了不同类型无砟轨道竖向耦合动力学模型,分别计算了整体式无砟轨道、板式无砟轨道以及浮置板式无砟轨道在列车运行下的振动响应。石蕊等[10]建立了钢弹簧浮置板轨道-箱梁桥三维有限元模型,以美国六级不平顺谱为激励,将轮轨力作为输入,对钢弹簧浮置板减振轨道的振动特性进行了研究。韩艺翚等[11]选取线路条件基本相同的断面,分别对圆形盾构隧道直线段和曲线段的钢弹簧浮置板道床以及对应的普通整体式道床进行现场测试,评价了钢弹簧浮置板道床的实际减振效果。吴道禹等[12]根据实际工程施工图纸,构建了钢弹簧浮置板轨道的有限元模型,对钢弹簧浮置板轨道在不同弹簧刚度、布置方式及载荷下浮置板轨道的模态频率和竖向位移进行了分析。
本文以在建杭州市地铁3号线下穿文教区段工程为研究对象,建立两种轨道结构型式的车辆-轨道竖向耦合动力学模型。利用有限元软件ABAQUS分析地铁运行时两种轨道的振动源强特性及其减振性能,评价浮置板长度、轨道不平顺、扣件刚度、钢弹簧刚度和行车速度对轨道结构动力特性的影响。
1 力学模型与计算条件
1.1 车辆-轨道耦合动力学模型
根据车辆-轨道耦合动力学理论,分别建立车辆-普通整体道床轨道竖向耦合动力学模型(见图1(a))和车辆-钢弹簧浮置板轨道竖向耦合动力学模型(见图1(b))。车辆-轨道耦合系统可分解为车辆和轨道两个子系统,并由轮轨接触关系实现二者在竖向的耦合。车辆系统从上至下依次包括车体、二系悬挂系统、构架、一系悬挂系统和轮对。普通整体道床轨道系统从上至下依次包括钢轨、扣件和基础,钢弹簧浮置板轨道系统从上至下依次包括钢轨、扣件、浮置板、钢弹簧和基础。
根据赫兹非线性弹性接触理论,轮轨接触力与位移关系可表示为
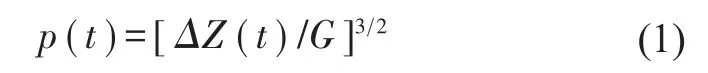
式中:△Z(t)为轮轨间弹性压缩量,G为轮轨接触常数,对于磨耗型踏面车轮,轮轨接触常数取值为G=3.86R-0.115× 10-8(m/N2/3),R为车轮半径(m)。
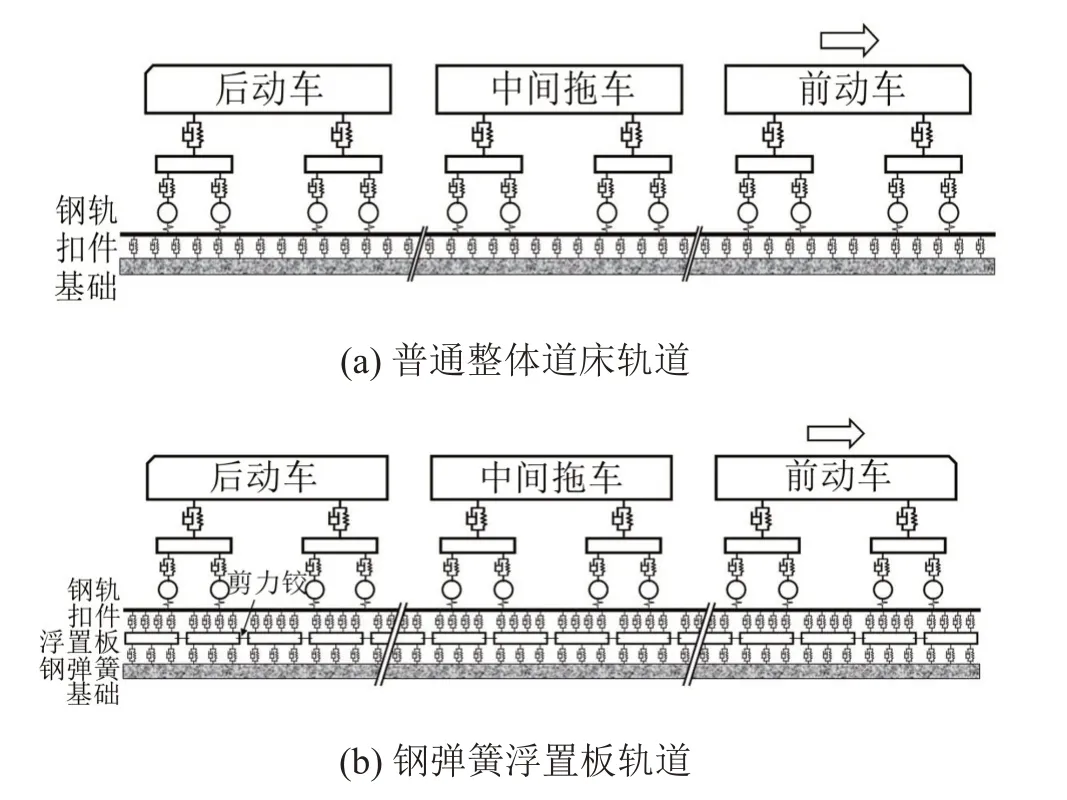
图1 车辆-轨道竖向耦合动力学模型
地铁车辆为AH型,由6节车体(2节动车和4节拖车)组成。考虑到车辆和轨道的对称性,以车辆和轨道的纵向对称轴为中心进行建模和分析。利用有限元软件ABAQUS,建立了整车和轨道的二维有限元模型。轨道总长400 m,图2为车辆-钢弹簧浮置板轨道有限元模型的局部放大图。一系悬挂、二系悬挂、扣件、钢弹簧采用弹簧/阻尼器单元,车体、转向架、钢轨、浮置板采用实体单元,车体和转向架作为刚体。钢弹簧底端固定,将轨道两端水平约束,列车以恒定速度行驶。普通整体道床轨道模型只需删除浮置板和钢弹簧单元,并固定扣件底端。
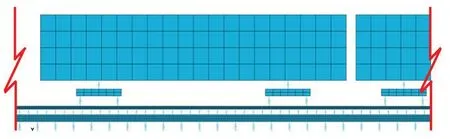
图2 车辆-钢弹簧浮置板轨道有限元模型局部放大图
对车辆-轨道系统,利用轮轨间的相互作用力平衡和几何相容条件,实现车辆与轨道的耦合。利用有限元软件ABAQUS,采用直接积分法,通过迭代计算,获得列车运行产生的系统动力响应,确定列车振动荷载的时程曲线(轮轨接触力、扣件支点力和钢弹簧支点力)。
1.2 模型参数
AH型车辆参数见表1。其中一、二系悬挂参数取自参考文献[13],其它参数由车辆制造厂提供。轨道结构参数见表2。参数取自参考文献[13-15]。地铁设计最大行车速度为80 km/h。
1.3 轨道不平顺
功率谱密度函数是表征轨道不平顺平稳随机过程中最常用的统计函数,可以表明轨道不平顺的大小随频率的变化。选取美国六级高低不平顺谱作为系统激励,利用MATLAB 编写了计算程序,由功率谱求出频谱的幅值和随机相位,再运用傅里叶逆变换求出轨道高低不平顺空间样本,如图3所示。
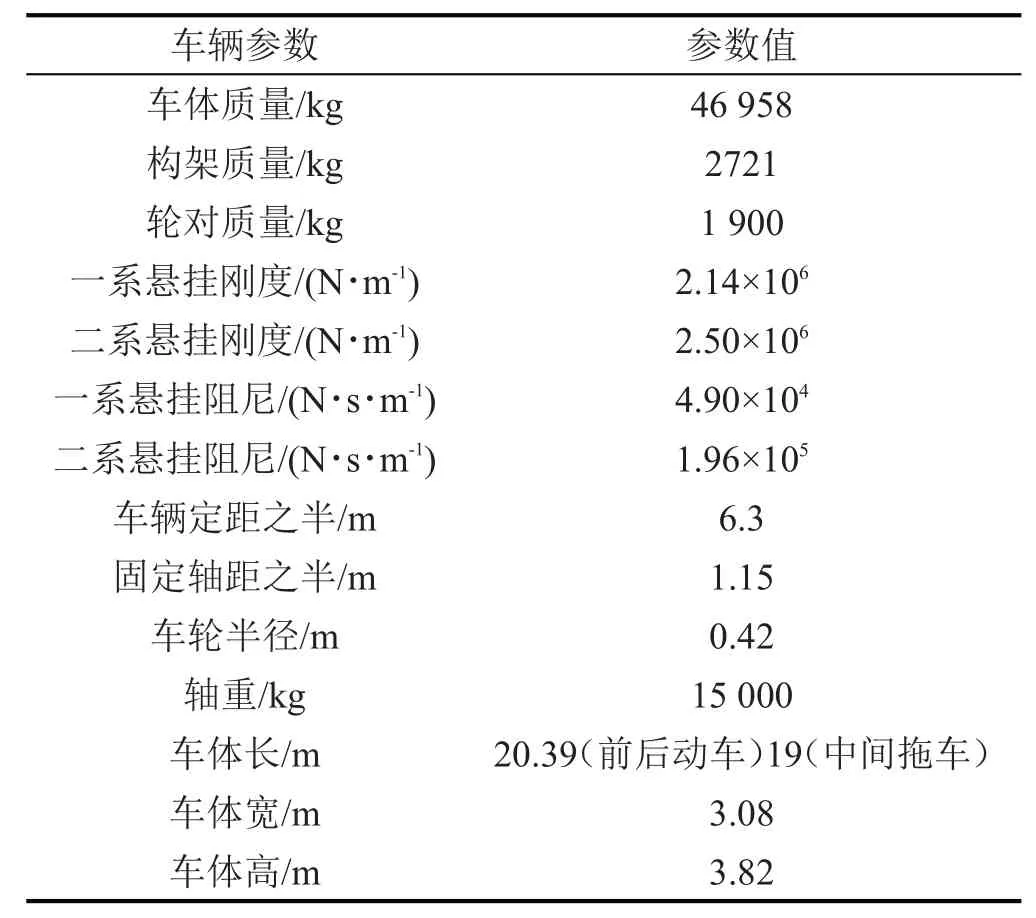
表1 地铁AH型车基本参数
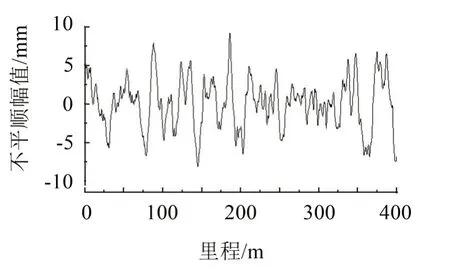
图3 轨道高低不平顺空间样本
2 轨道振动源强特性
2.1 有不平顺激励的普通整体道床轨道动力响应
图4为有不平顺激励的普通整体道床轨道的动力响应,其中图4(a)为钢轨竖向加速度时程曲线,图4(b)为钢轨竖向位移时程曲线,图4(d)为轨道支点力(包含静力部分)时程曲线。从图4(a)和图4(b)可以看出,当6节车体依次经过钢轨观测点时,观测点处的钢轨加速度和位移大幅度增加。
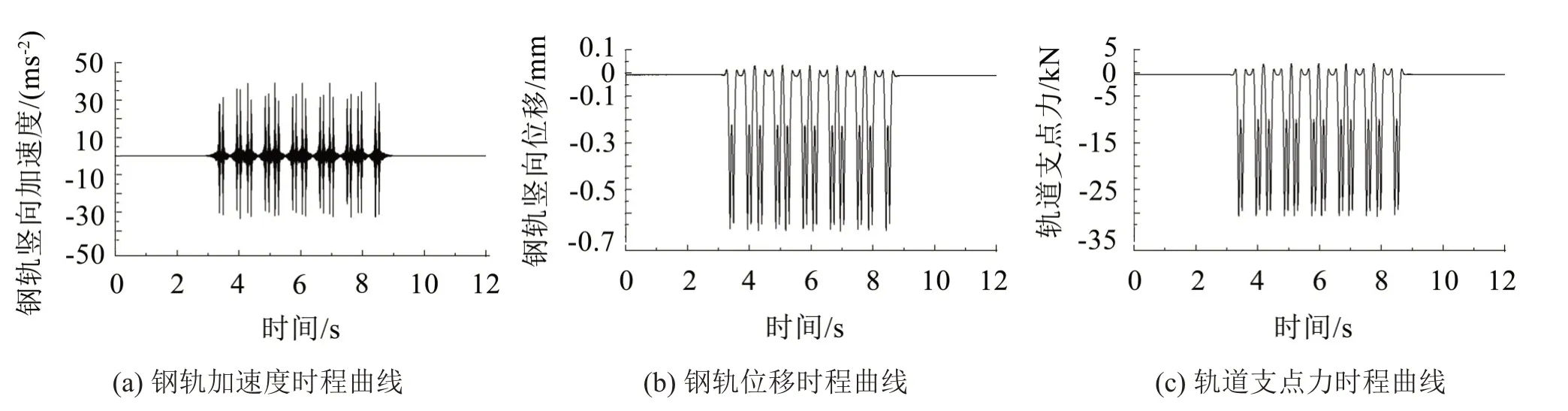
图4 有不平顺激励的普通整体道床轨道动力响应
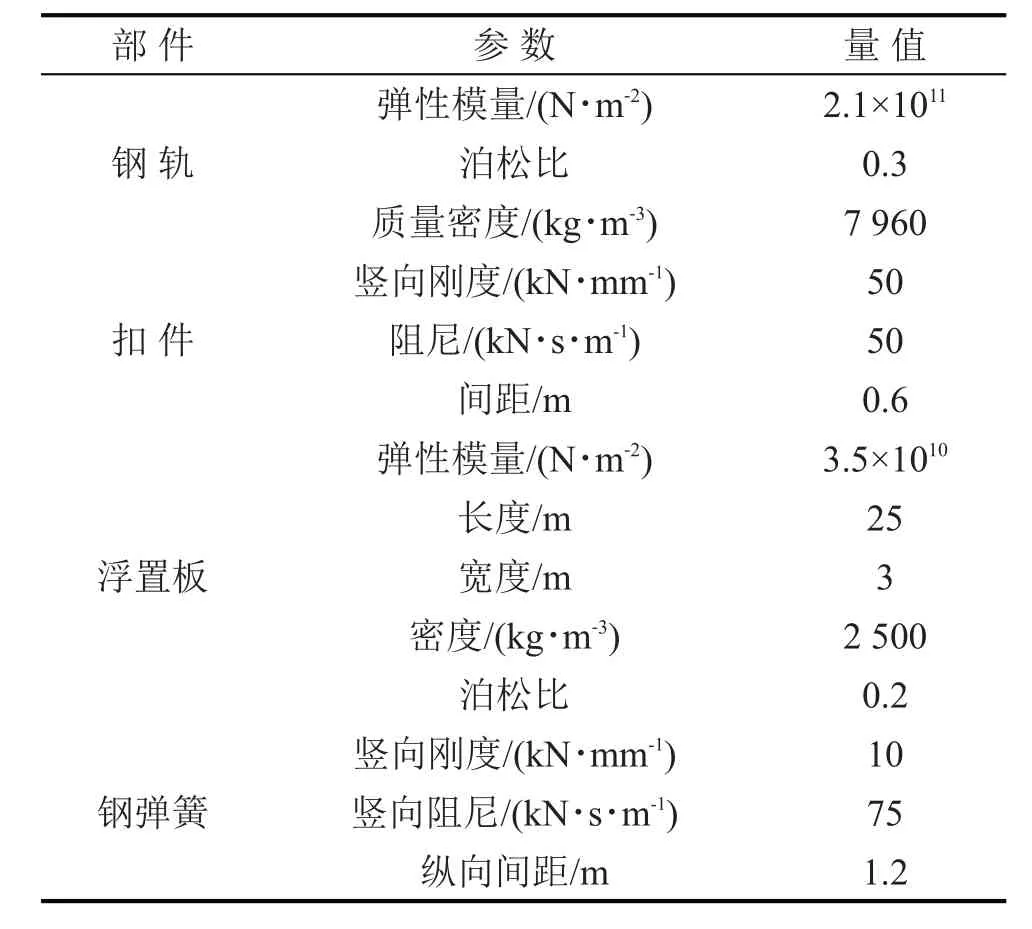
表2 轨道结构基本参数
从图4(c)可以看出,当轮对经过观测点处时,轨道支点力就会出现很大的增幅,且各轮对经过观测点处时的支点力峰值基本相同,最大动支点力(不包含静力部分)为30 kN。另外,从图4(a)至图4(c)可以看出,由于普通整体道床轨道的刚度较大,加速度、位移和支点力响应的高频成份都比较丰富。
2.2 有不平顺激励的非连续浮置板轨道动力响应
图5为有不平顺激励的非连续浮置板轨道的动力响应,其中图5(a)至图5(d)分别为钢轨和浮置板竖向加速度、竖向位移的时程曲线,图5(e)为钢弹簧支点力时程曲线。计算中,浮置板长度取25 m,并且不考虑剪力铰的影响。从图5(a)可以看出,当6节车体依次经过钢轨观测点时,观测点处的钢轨加速度明显增大。从图5(b)可以看出,在钢轨观测点正下方的浮置板观测点处,当车体依次经过时,浮置板加速度也呈现增长趋势,但与钢轨加速度相比,增长幅度非常有限,其峰值远小于钢轨的加速度峰值。从图5(c)和图5(d)的比较可以看出,由于钢轨受扣件和钢弹簧的双重影响,钢轨的位移峰值略大于浮置板的位移峰值。从图5(e)可以看出,当轮对经过钢弹簧观测点处时,钢弹簧支点力将大幅度增加,且中间拖车轮对经过观测点处时,钢弹簧支点力将达到最大值,最大动支点力为28 kN。
另外,从图4和图5的比较可以看出,两种轨道结构的钢轨加速度基本相同,但钢轨位移相差很大。由于浮置板和钢弹簧的存在,钢弹簧浮置板轨道的钢轨位移峰值是普通整体道床轨道的7倍左右。并且,将普通整体轨道的扣件支点力与浮置板轨道的钢弹簧支点力进行比较,可以看出,虽然两者峰值相近,但扣件数量是钢弹簧数量的两倍,因此钢弹簧浮置板轨道向隧道传递的力约为普通整体道床轨道的0.5倍,说明钢弹簧浮板结构具有良好的减振效果。
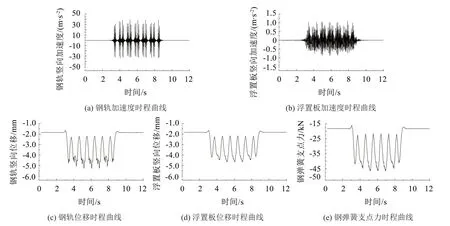
图5 有不平顺激励的非连续浮置板轨道动力响应
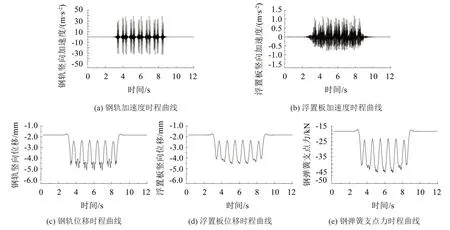
图6 有不平顺激励的连续浮置板轨道动力响应
2.3 有不平顺激励的连续浮置板轨道动力响应
图6为有不平顺激励的连续浮置板(无限长浮置板)轨道的动力响应,其中图6(a)所示的钢轨加速度和位移大幅度增加。图6(d)分别为钢轨和浮置板竖向加速度、竖向位移的时程曲线,图6(e)为钢弹簧支点力时程曲线。从图5和图6的比较可以看出,当车体依次经过各结构的观测点时,连续浮置板轨道的加速度、位移和支点力响应与非连续浮置板轨道的加速度、位移和支点力响应基本一致,最大动支点力为27 kN。由于带剪力铰的非连续浮置板刚度处于不带剪力铰的非连续浮置板刚度与连续浮置板刚度之间,因此以上结果说明浮置板长度和剪力铰对轨道动力响应的影响不大。
2.4 无不平顺激励的连续浮置板轨道动力响应
图7为无不平顺激励的连续浮置板轨道的动力响应,其中图7(a)至图7(d)分别为钢轨和浮置板竖向加速度、竖向位移的时程曲线,图7(e)为钢弹簧支点力时程曲线。从图6和图7的对比可以看出,不考虑不平顺激励时,钢轨和浮置板的加速度明显小于有不平顺激励的相应值,而钢轨和浮置板的位移及钢弹簧的支点力接近于有不平顺激励的相应值,最大钢弹簧动支点力为26 kN。
3 结构参数和行车速度对轨道动力特性的影响
3.1 扣件刚度的影响
在其它参数不变的情况下,扣件刚度分别取10 kN/mm、30 kN/mm、50 kN/mm、70 kN/mm、100 kN/mm,计算得到的钢弹簧浮置板轨道最大动力响应见图8(a)至图8(c),浮置板位移几乎没有变化,而钢轨位移急剧减小,并逐渐接近浮置板位移。从图8(b)和图8(c)可以看出,虽然钢轨和浮置板加速度以及钢弹簧支点力随扣件刚度的增大而增大,但变化幅度很小,因此扣件刚度对它们的影响基本上可以忽略。
3.2 钢弹簧刚度的影响
在其它参数不变的情况下,钢弹簧刚度分别取1 kN/mm、5 kN/mm、10 kN/mm、15 kN/mm、20 kN/mm,计算得到的钢弹簧浮置板轨道最大动力响应见图9(a)至图9(c)。从图9(a)可以看出,随着钢弹簧刚度的增加,钢轨和浮置板的位移明显减小,并且两者非常接近。从图8(b)可以看出,钢弹簧刚度对钢轨和浮置板加速度的影响较小。从图9(c)可以看出,随着钢弹簧刚度的增加,钢弹簧支点力明显增大。因此,在不影响轨道系统稳定性条件下,钢弹簧刚度尽量取小值。
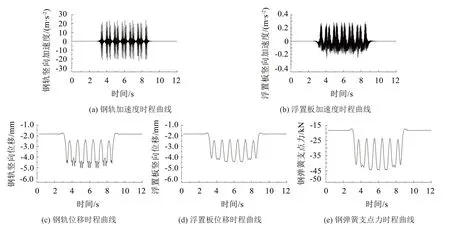
图7 无不平顺激励的连续浮置板轨道动力响应
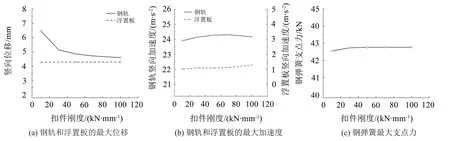
图8 扣件刚度对轨道动力响应的影响
3.3 行车速度的影响
在其它参数不变的情况下,行车速度分别取40 km/h、60 km/h、80 km/h、100 km/h 和120 km/h,计算得到的钢弹簧浮置板轨道最大动力响应见图10(a)至图10(c)。由图10(a)至图10(c)可以看出,随着行车速度的增大,钢轨和浮置板的位移以及钢弹簧支点力的变化不大,而钢轨和浮置板的加速度有较大增加。
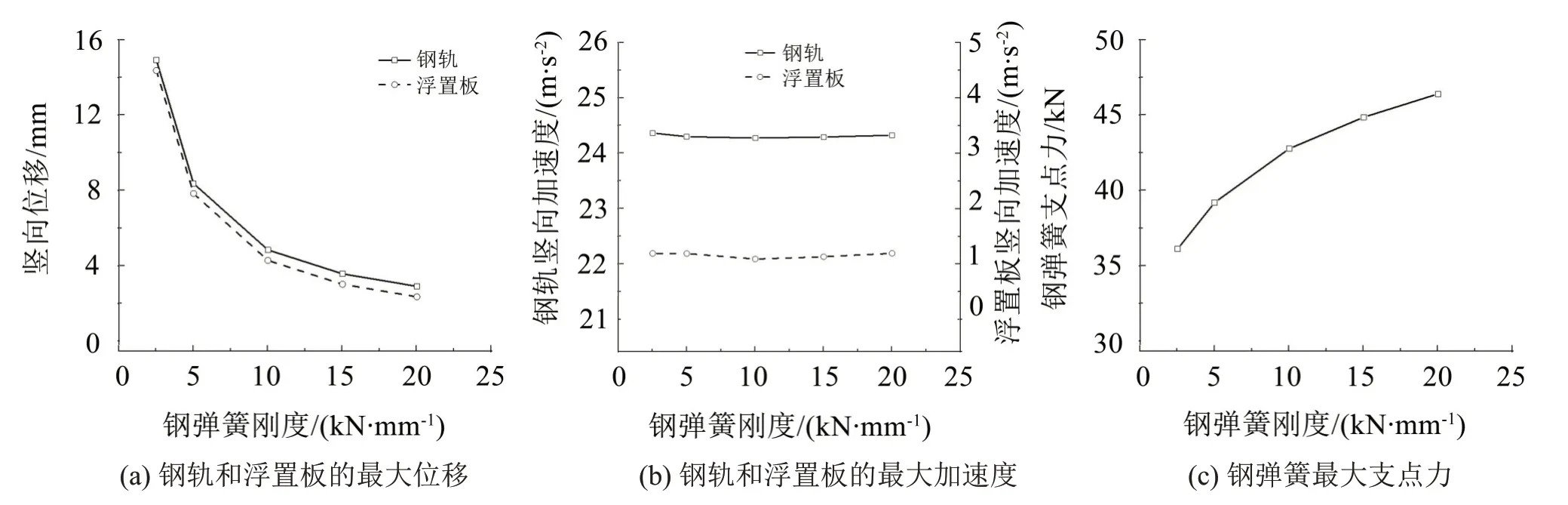
图9 钢弹簧刚度对轨道动力响应的影响
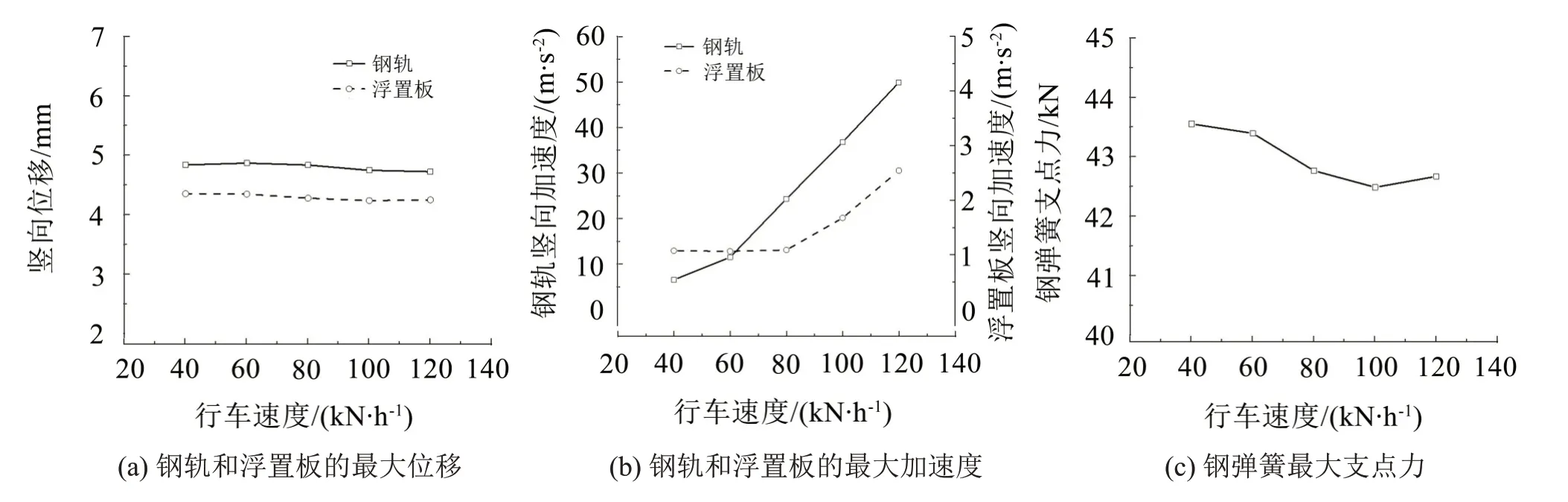
图10 行车速度对轨道动力响应的影响
4 结语
根据车辆-轨道耦合动力学理论,建立了两种轨道结构的车辆-轨道耦合动力学模型,利用有限元软件ABAQUS 计算分析了在轨道不平顺激励下的轨道动力响应,可以得出以下结论:
(1)普通整体道床轨道和钢弹簧浮置板轨道的钢轨加速度基本相同,但位移相差较大。钢弹簧浮置板结构能有效降低车辆-轨道系统向隧道传递的地铁振动荷载,具有良好的减振效果。
(2)非连续浮置板轨道与连续浮置板轨道的动力响应基本一致,说明浮置板长度和剪力铰对钢弹簧浮置板轨道动力响应的影响不大。
(3)轨道不平顺对钢轨和浮置板的加速度影响较大,对钢轨和浮置板的位移及钢弹簧的支点力影响较小。
(4)扣件和钢弹簧的刚度对钢轨和浮置板的位移影响较大,对加速度影响较小。扣件刚度对钢弹簧支点力的影响较小,而钢弹簧刚度对钢弹簧支点力的影响较大。因此,在选择钢弹簧浮置板轨道的结构参数时,应综合考虑各参数对轨道系统稳定性和减振性能的影响。
