基于SARAX-LAVENDER的快堆光子释热行为分析
2021-04-16陈建达郑友琦杜夏楠吴宏春
陈建达,郑友琦,杜夏楠,吴宏春
(西安交通大学 核科学与技术学院,西安710049)
反应堆中的释热由中子释热和光子释热2部分组成[1]。在传统的金属冷却快增殖堆中,光子释热约占总释热的13%[2]。不同类型的组件中,光子的释热份额各不相同。在非燃料区且中子通量密度较低的区域,如反射层组件、控制棒、屏蔽层和结构材料等,几乎所有的释热都来自光子的贡献。传统的释热计算,或仅考虑中子的释热贡献,或假定光子不进行输运就地沉积,均会低估非燃料区的释热水平。在快堆的核设计中,热应力计算、冷却剂流量分配和非燃料组件的释热率计算等均涉及光子的释热率分布,迫切需要开发一个适用于快堆核设计的光子释热率计算程序。
SARAX-LAVENDER,简称LAVENDER,是西安交通大学NECP实验室自主研发的适用于先进反应堆中子学分析系统的堆芯计算程序[3-4],具有针对快堆特点的临界计算、燃耗计算、反应性计算、临界棒位搜索、重启动和换料等功能,尚不具备求解中子-光子耦合输运方程和精确计算堆内光子释热率分布的功能。本文基于中子输运理论、光子输运理论和中子-光子数据库的制作,开发了中子-光子耦合输运模块和利用比释动能因子精确计算堆内光子释热率分布与总释热率分布的计算模块,并对比分析了设计模块与HYDRA程序及蒙特卡罗程序的计算结果。
1 理论模型和计算流程
1.1 多群中子-光子数据库的制作
用于LAVENDER输运计算的多群中子-光子耦合数据库结构如图1所示。其中,对于大部分核素,(γ,n)截面一般为0,所以,光子与材料发生反应所产生的中子对中子源的贡献很小,可以忽略不计。因此在中子输运过程中,可以不考虑(γ,n)截面所带来的影响。
在裂变反应堆中,光子的产生途径主要是中子与靶核发生作用,靶核退激后放出光子。中子产生光子的主要反应道,如表1所列。

图1 多群中子-光子耦合数据库结构[5]Fig.1 Arrangement of multi-group neutron(n) andgamma(γ) cross sections in a coupled transport table[5]

表1 中子产生光子的反应道Tab.1 Gamma production through neutron reaction
光原子截面是光子与核外电子发生相互作用概率大小的量度,不具有共振现象,制作光原子截面时仅需对核数据评价库中的数据进行线性化处理和能群归并。且多群光原子截面依赖于元素,即同一元素的所有同位素具有相同的光原子截面,所以,在加工光原子截面时,仅需使用核数据加工程序NJOY对不同的元素进行处理。在中子-光子耦合输运过程中,需要使用的多群光原子截面包括光子总截面、相干散射矩阵、非相干散射矩阵和电子对产生矩阵。
用于输运计算的多群中子截面是由少群常数产生程序SARAX-TULIP(TULIP)制作产生的。TULIP程序从点截面数据库和多群数据库出发,利用超细群方法处理共振,采用碰撞概率方法进行组件的输运计算[6]。TULIP程序已经过多个基准题验证,可满足快堆的计算精度要求。
在进行释热率分布计算时,需要使用中子和光子各自的比释动能(kinetic energy released in material, KERMA)因子[7]。本文通过NJOY程序制作产生光子和中子各自的KERMA因子。光子不存在共振效应,且截面不随背景截面和温度而发生变化,因此,通过NJOY程序加工后的光子KERMA因子,可以直接用于计算堆芯的光子释热率。中子存在极为复杂的共振效应,需要对NJOY程序加工后的结果进行处理,才能得到考虑自屏的中子KERMA因子kn,用于计算反应堆内的中子释热率。kn的计算公式为
定义 2[9] Hom-Jordan李代数(L,[·,·]L,α,δ)由空间L,一个二元双线性运算L×L→L满足
(1)
其中,kn(NJOY)为用NJOY程序加工后的与背景截面和温度相关的KERMA因子;σn(NJOY)为用NJOY程序加工后的与背景截面和温度相关的中子微观截面;σn(TULIP)为组件程序TULIP产生的有效自屏中子截面。
中子释热率与光子释热率相加,即为堆芯内的总释热率。
1.2 功率计算
LAVENDER程序中的中子释热率和光子释热率计算流程,如图2所示。LAVENDER程序采用离散节块方法求解中子输运方程,基本出发点是对中子通量密度的角度分布在一些离散的方向上进行求解,在空间度量上,采用粗网节块和节块内的多项式展开进行离散。
首先,通过材料和几何信息求解中子输运方程,获得各个节块的33群中子通量密度φi,g,其中,i,g分别为空间节块编号和能群编号。
其次,求解式(2)得到各个节块的光子源项。
(2)
其中,Ni,e为第i个节块核素e的核子密度;σi,e,x,g为TULIP程序产生的关于x反应的多群微观中子截面;χe,x(g,gγ)为光子产生截面,表示第g群中子与核素e发生x反应产生第gγ群光子的概率。
将计算得到的Si,gγ当作固定源,并对散射源项和光子总截面进行输运修正处理[8]。
(3)
(4)
σtr,s,gγ→gγ′=σs,0,gγ→gγ′(gγ′≠gγ)
(6)
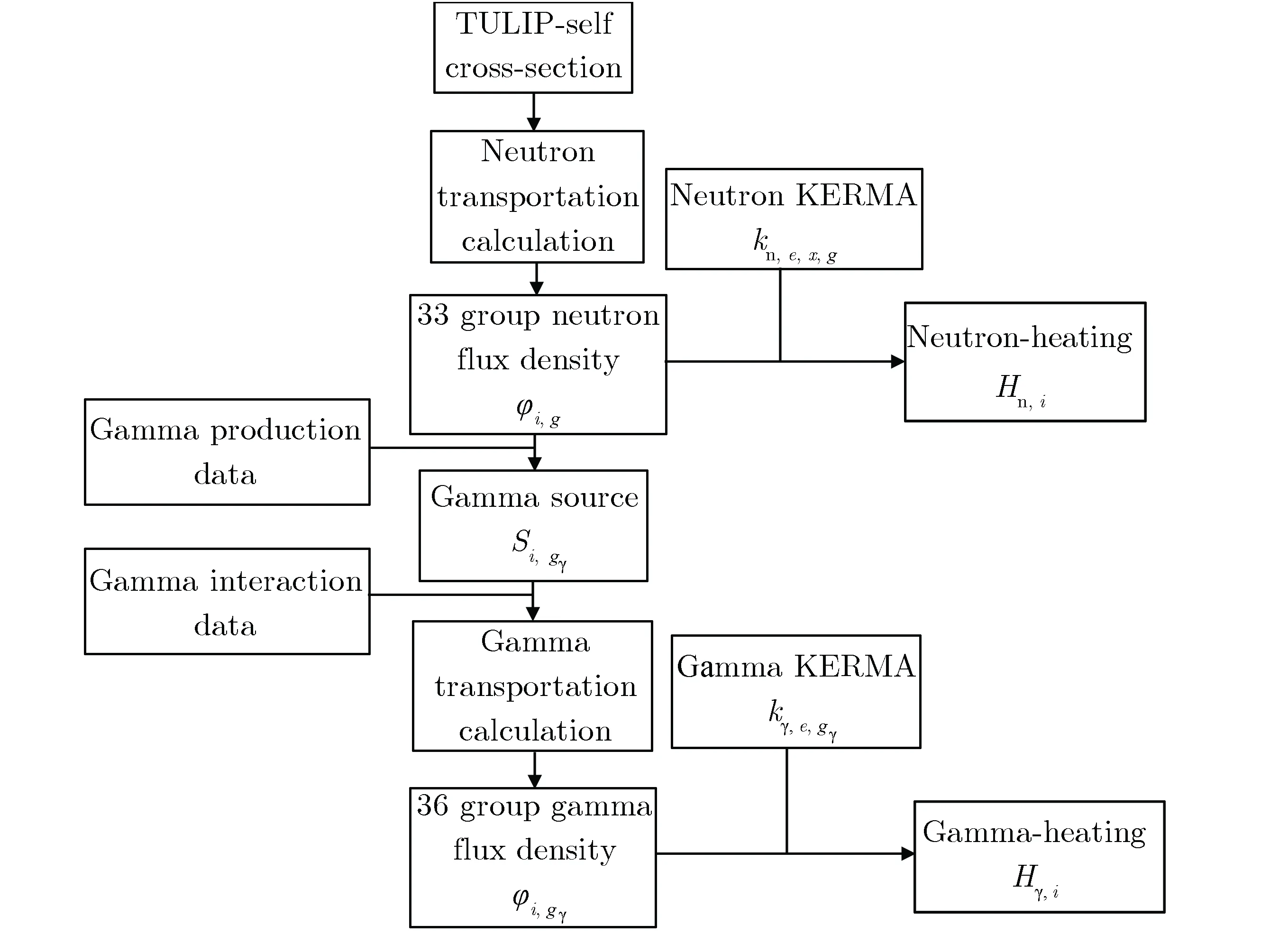
图2 LAVENDER程序中的中子释热率和光子释热率计算流程Fig.2 Flow chart of detailed neutron- and γ-heating calculations in LAVENDER
尽管光子具有波粒两重性,但一般在光子能量极低的情况下才表现出波的特性。在核能领域中,可将光子当作中性点粒子进行处理,光子在介质内运动时,可不考虑其受核的电磁作用力的影响,也可忽略量子力学效应,光子在介质内的运动符合玻耳兹曼方程。因此,可以仿照中子输运方程,得到多群稳态光子输运修正方程为
其中,Σtr,gγ为宏观输运修正总截面;Σtr,s,gγ′→gγ为宏观输运修正散射截面;Ωm为运动的单位方向矢量;Ψm,gγ为光子角通量密度;φgγ′为光子通量密度;Sgγ′为外光子源项。中子-光子耦合输运计算中有2种耦合方式:一是在中子输运迭代收敛后,先利用收敛的中子通量密度分布进行光子源项计算,再使用光子源项进行光子输运计算;二是中子输运和光子输运耦合迭代,考虑光子输运对中子源项的贡献,但对大部分核素,由于光子产生中子的截面一般为零,故光子对中子源项的贡献很小可以忽略不计。因此,2种耦合方式的计算结果相差很小,本文LAVENDER程序中使用第1种耦合方式。
通过数值求解中子-光子耦合输运方程,可以得到33群的中子通量密度φi,g和36群的光子通量密度φi,gγ。则中子释热率、光子释热率和总释热率的计算公式为
(8)
(9)
Hi=Hi,n+Hi,γ
(10)
其中,Hi,n,Hi,γ分别为第i个节块的中子释热率和光子释热率,W·cm-3;kn,e,x,g为核素e发生x反应的中子KERMA因子;kγ,e,gγ为核素e的光子KERMA因子;Hi为第i个节块的总释热率, W·cm-3。
2 数值结果与分析
为验证中子-光子输运模块的正确性,选择一个全反射堆芯作为算例。堆芯布置如图3所示。其中,中间材料为燃料,外圈为反射层,整个堆芯由20×20×20个节块组成。
LAVENDER程序具有使用其他数据库截面的功能,因此,使用BUGLE96数据库的中子-光子截面,对算例的keff和归一化光子通量密度进行计算,并与中子-光子耦合输运程序HYDRA[9]的相应计算结果进行对比,以验证LAVENDER程序中子-光子输运模块的正确性。HYDRA程序是NECP实验室开发的基于细网差分的大规模并行计算程序,具备压水堆pin-by-pin计算、堆外探测器响应函数计算、屏蔽计算和中子-光子耦合输运计算等功能。图4为堆芯虚线上所有组件的归一化光子通量密度分布。

图3 全反射堆芯布置Fig.3 Core configuration with reflective boundarycondition imposed on all boundaries

图4 堆芯虚线上所有组件的归一化光子通量密度分布Fig.4 The normalized gamma flux density distribution of all assemblies on the vertical line of the core
由图4可见,用LAVENDER程序和HYDRA程序计算的归一化光子通量密度基本相同,对于大部分节块,这2种程序计算结果的相对偏差均小于1%;相对偏差极大值约为4.3%,出现在材料交界处的节块中,这主要是由于HYDRA程序与LAVENDER程序在材料交界处的网格划分粗细程度不同造成的。
在使用同一套截面数据下,用LAVENDER程序和HYDRA程序计算得到的keff分别为2.206 09和2.206 49,二者的相对偏差为0.018%。
为了验证LAVENDER程序中子-光子截面库和释热率计算模块的适用性和合理性,用LAVENDER程序和MCNP程序分别对图5所示堆芯各个组件的归一化光子释热率和归一化总释热率进行了计算。图5堆芯内区包含20根燃料组件和5根控制棒,在燃料外围布置2圈共56根增殖组件,在堆芯最外区布置88根反射层组件。由于该堆芯是1/8对称,因此,只需对1/8堆芯进行计算。

图5 对称堆芯布置Fig.5 Configuration of symmetrical core
图6给出了LAVENDER程序与MCNP程序计算的归一化光子释热率分布对比。

图6 LAVENDER程序与MCNP程序计算的归一化光子释热率分布对比Fig.6 Normalized gamma-heating distributions calculatedby LAVENDER and MCNP, respectively
由图6可见,LAVENDER程序与MCNP程序计算的堆芯内的归一化光子释热率分布大致相同,二者的相对偏差均小于3.4%。
图7给出了LAVENDER程序和MCNP程序计算的归一化总释热率分布对比。
由图7可见,2种程序计算结果的最大相对偏差出现在最边角的组件上,约为10.5%;对于其他边界组件,相对偏差均小于8.2%;对于内区的燃料组件、增殖组件和控制棒组件,最大相对偏差均小于3%。分析认为, 2种程序计算结果之间的偏差主要来自中子释热的计算, 可能是由于LAVENDER程序中计算中子释热的KERMA因子与MCNP程序中计算中子释热的能量转移截面不同造成的。最边角组件的释热绝对值低,导致相对偏差较大。
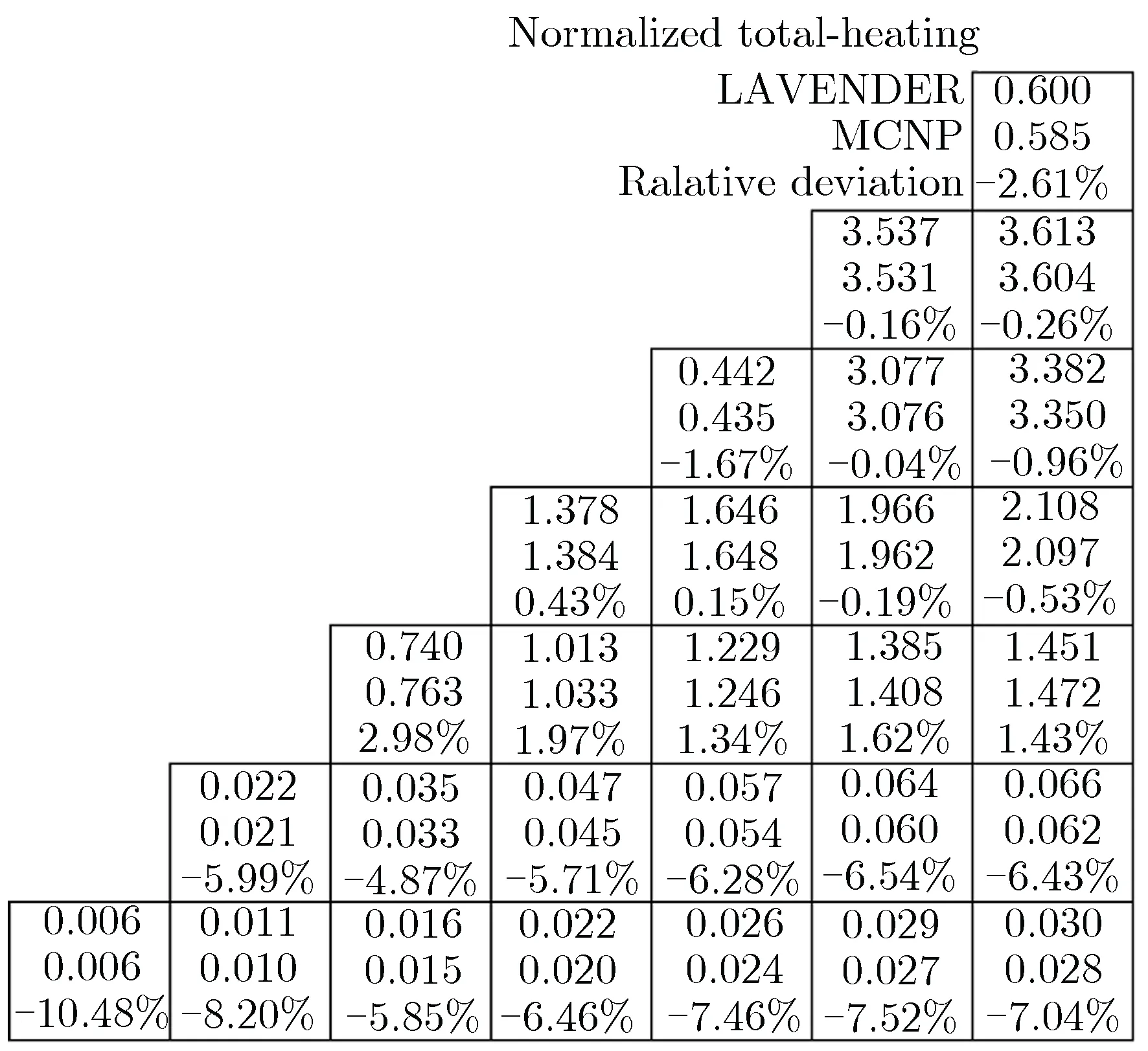
图7 LAVENDER程序与MCNP程序计算的归一化总释热率分布对比Fig.7 Normalized total-heating distributions calculatedby LAVENDER and MCNP, respectively
表2给出了LAVENDER程序和MCNP程序计算的各类型组件及堆芯的光子释热份额。

表2 利用LAVENDER程序和MCNP程序计算的各类型组件及堆芯的光子释热份额Tab.2Gamma-heating fractions in different assemblies and core calculated by LAVENDER and MCNP, respectively
由表2可见,整个堆芯中约10%的释热贡献来自光子;反射层组件中约80%的释热由光子产生;控制棒组件中约20%的释热来自光子;增殖组件和燃料组件中,由于中子裂变反应释放的能量较大,因此,光子的释热份额较低,仅约10%。2种程序计算结果之间的相对偏差小于8%。
3 结论
本文在快堆堆芯计算程序LAVENDER的基础上,制作了中子-光子数据库,开发了中子-光子耦合输运模块和释热率计算模块,通过和HYDRA程序及MCNP程序计算结果的对比,对开发模块进行了验证。结果表明,LAVENDER程序的中子-光子耦合输运计算是正确的,光子释热率计算结果与MCNP程序的计算结果符合较好,反应堆堆芯中的光子释热份额较大,约占10%。
目前,还无法直接应用核数据处理程序制作缓发光子产生截面,后续将进一步探索缓发光子产生截面的制作,提升利用KERMA因子计算释热率的精度。
