某型号起落架撑杆稳定性分析

李 薇，郭 辉，韩持刚，于新鹏

(中航飞机起落架有限责任公司，陕西 汉中 723200)

撑杆作为主起落架的一个关键组件，与机身连接，承担着主起落架部分冲击载荷，起着主起支柱与机身间载荷传递，约束支柱外筒相对机身转动的作用。起落架放下时，撑杆展开并上锁将主起支柱锁定在放下位置，从而使其能够承受航向和垂向载荷；主起支柱收上时，撑杆在主起撑杆作动筒(以下简称撑杆作动筒)的驱动下开锁后折叠，与主起支柱协调运动，一同收入主起落架舱内。其稳定性对主起落架的收上、放下过程起着关键作用，并直接影响着飞机的起飞、着陆安全。因此，找到影响撑杆稳定性的因素并进行控制，对飞机的安全性能至关重要[1-2]。

1 撑杆的工作机理

1.1 撑杆的结构组成

撑杆主要由上撑杆组件、下撑杆组件、连杆、摇臂、撑杆作动筒、接头、铰接螺栓和螺母等零件组成(见图1和图2)，成对安装在飞机主起支柱上。组成撑杆的零组件基本一致，仅个别零件因结构左右对称有所区分。

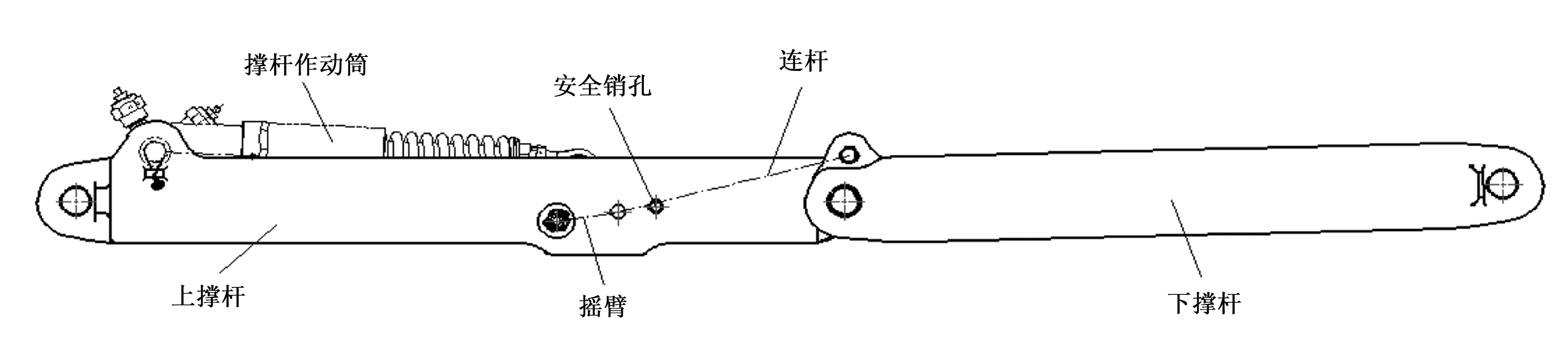
图1 上锁状态

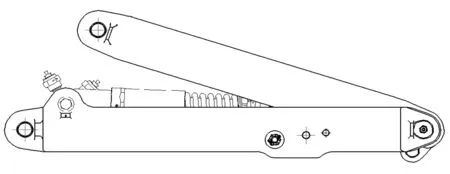
图2 开锁状态

上撑杆一端双耳片与安装在机身上的接头铰接，另一端双耳片与下撑杆铰接，中部设有与摇臂连接的孔及安装地面安全销的通孔。下撑杆未与上撑杆连接的一端单耳片与主支柱上的接头铰接。铰接的上、下撑杆设有向上的偏心距e1=(6.2±0.3) mm，连杆和摇臂设有向下的偏心距e2=(7±0.5) mm，偏心距可通过调整连杆的长度及调节片的厚度保证。

1.2 撑杆的工作原理

1.2.1 放下主起落架时撑杆的上锁及展开原理

飞机主起落架放下过程中，在放下作用力的驱动下，上、下撑杆展开，当连杆和摇臂铰接点的偏心距e2变为0时，上、下撑杆的展开受到限制，此时一直作用在摇臂上的撑杆作动筒的弹簧力会使摇臂产生顺时针旋转；当摇臂转动到与上撑杆止动时，偏心距e1、e2最终形成，撑杆锁上锁(见图1)，将主支柱锁定在放下位置。

1.2.2 收起主起落架时撑杆的开锁及折叠原理

飞机收起主起落架时，撑杆作动筒在液压力的作用下回缩，带动摇臂逆时针转动，使e2值减小；当e2值减小至0并开始变为负值时，撑杆锁实现开锁(见图2)，并在主起支柱收上的作用力驱动下向上折叠，与主起支柱协调运动，一起收入起落架舱内。

2 撑杆偏心距的调整

2.1 传统偏心距调整方式

传统撑杆调整方式，主要借助工艺装备(专用检测装置、专用装配夹具、工艺销轴以及专用工艺连杆)将以上零组件在平台上按设计图样组装起来(组件铰接原理如图3所示)，通过高度尺和块规进行尺寸检测分析。在偏心距调整过程中，需频繁调节连杆中心距及垫片厚度，保证设计要求的偏心距e1=(6.2±0.3) mm和e2=(7±0.5) mm。传统方法调整繁琐，调整耗时长且效率较低。

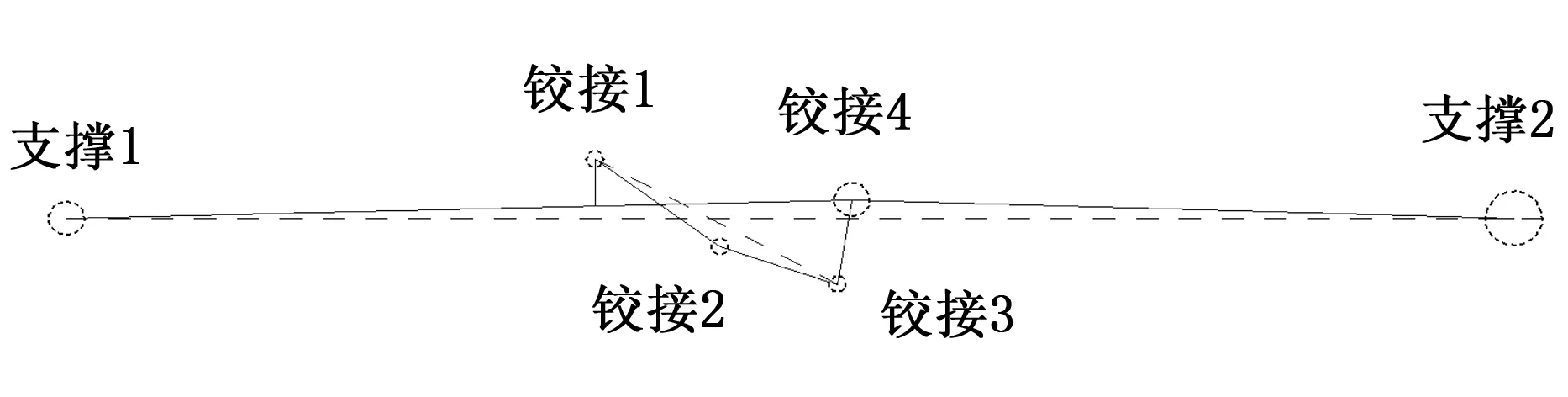
图3 组件铰接原理示意图

2.2 基于CATIA软件尺寸驱动的偏心距调整

在CAITA软件零件设计模块中，按零组件关联的孔心距名义尺寸及相关角度构建装配关系(见图3)，通过尺寸驱动获得e1、e2值。可将基体尺寸选为变量，每次递增0.01 mm，分别对e1、e2进行测量，通过数据(见表1)和拟合线图(见图4)可知：任一零件基本尺寸变化与偏心距大小变化呈线性比例。摇臂组件上的尺寸(110±0.05) mm变化、连杆上的尺寸84.5～85.5 mm的变化与e1、e2的变化比例相同，均为1∶0.2∶6的比例关系，对偏心距值的影响也最明显；上撑杆组件上的尺寸(40±0.05) mm变化和下撑杆组件上的尺寸(55.1±0.05) mm变化对偏心距值的影响偏小；表1中e1与e2值的变化均为反比，即e1越大，e2越小。

表1 基本尺寸对偏心距的影响

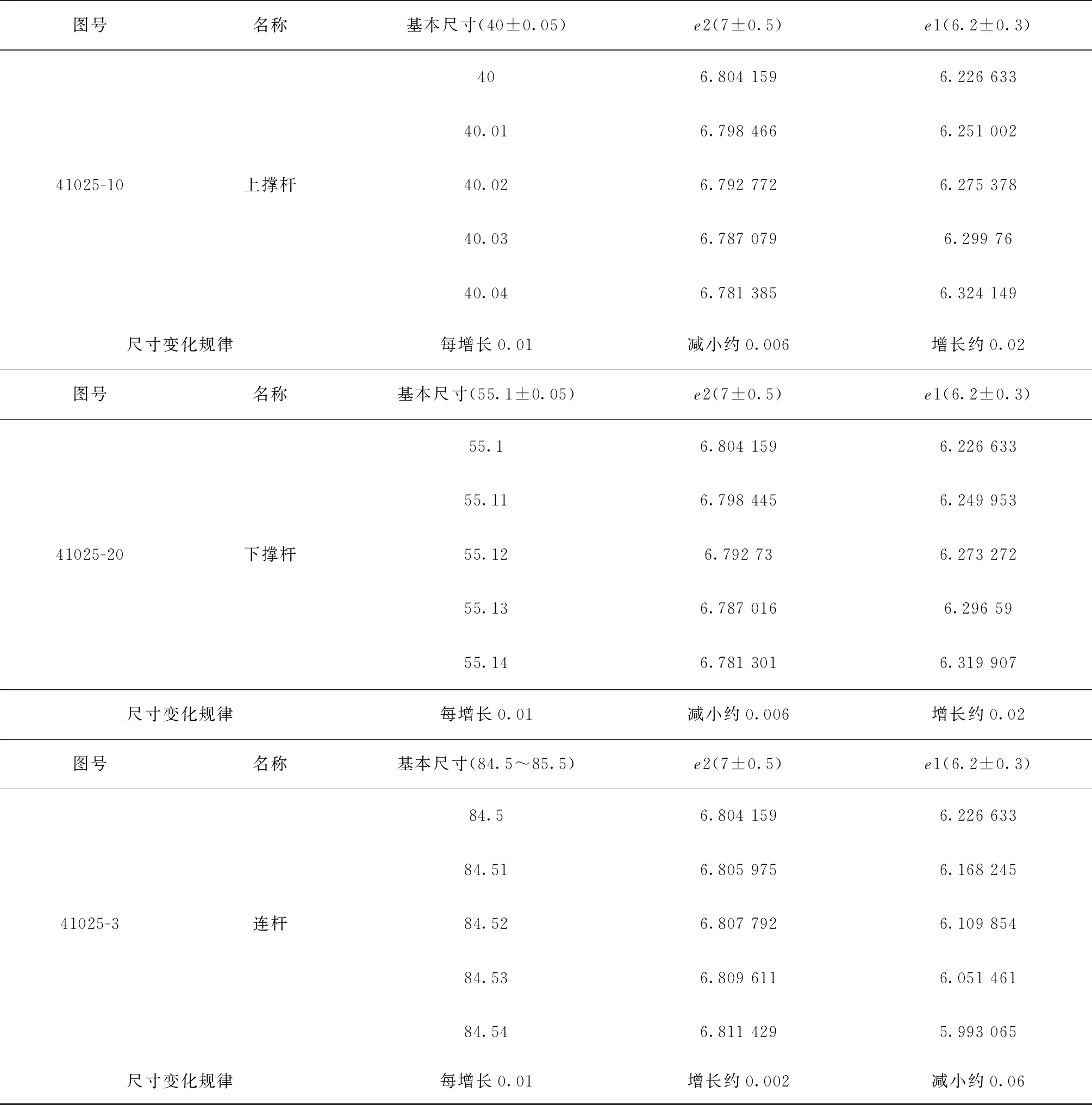
(续表)

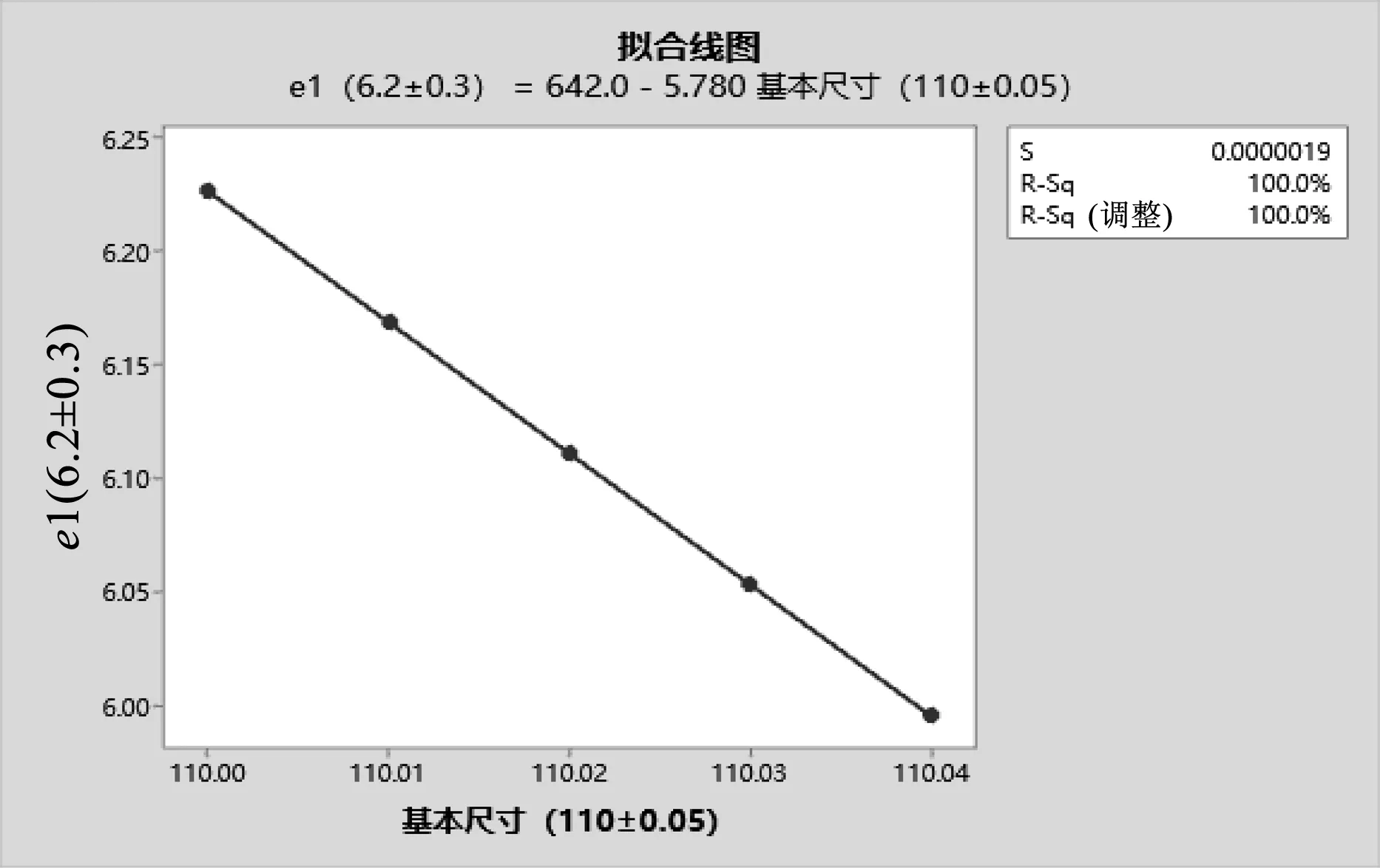
a)偏心距e1

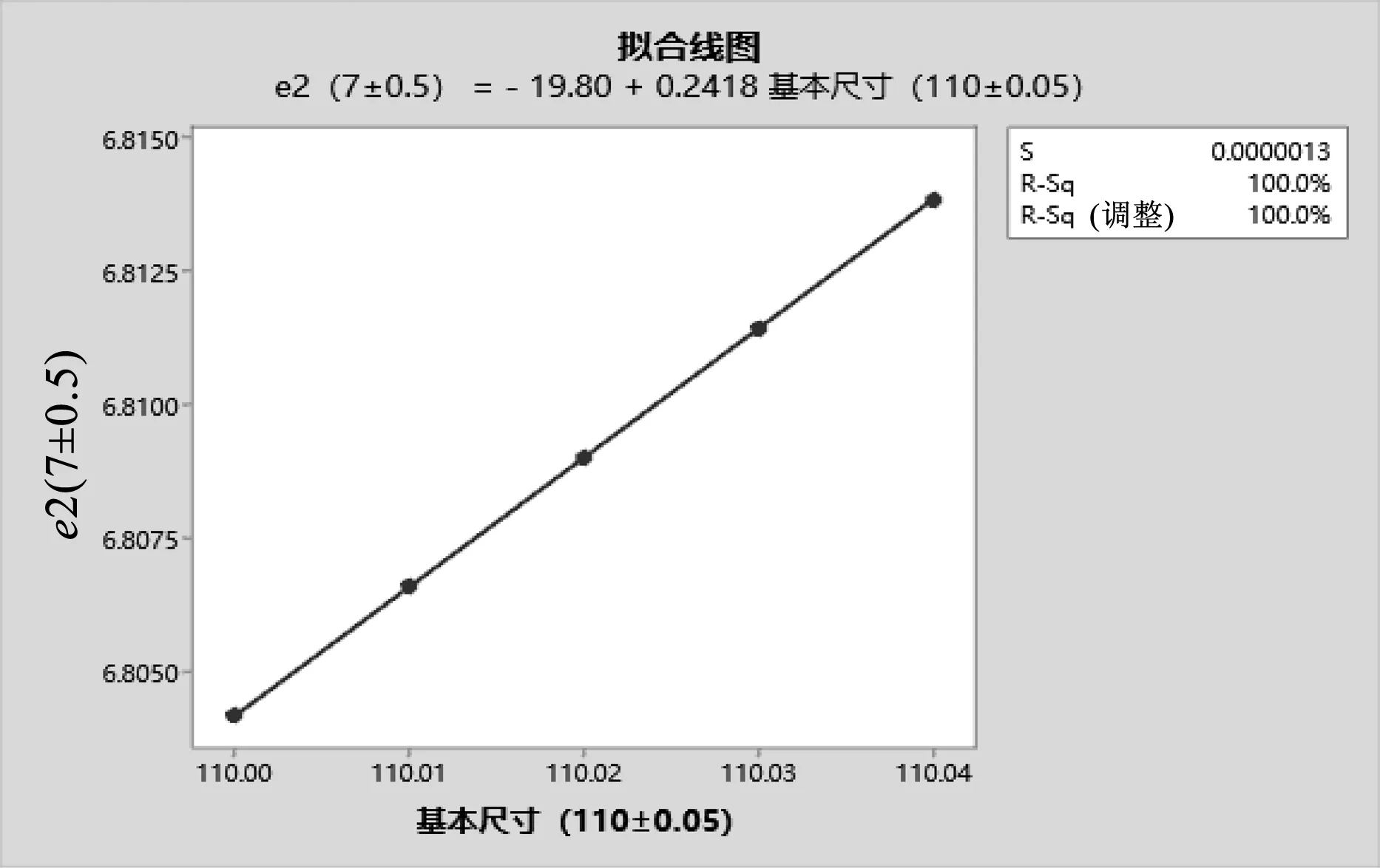
b)偏心距e2

在设定e1、e2值的大小时，同样采用尺寸驱动求解法，求解连杆中心距大小。此时，角度57.17°为封闭环，其余尺寸链约束不变，同时改变e1和e2，通过尺寸驱动可测量出连杆中心距与角度新值(见表2)。

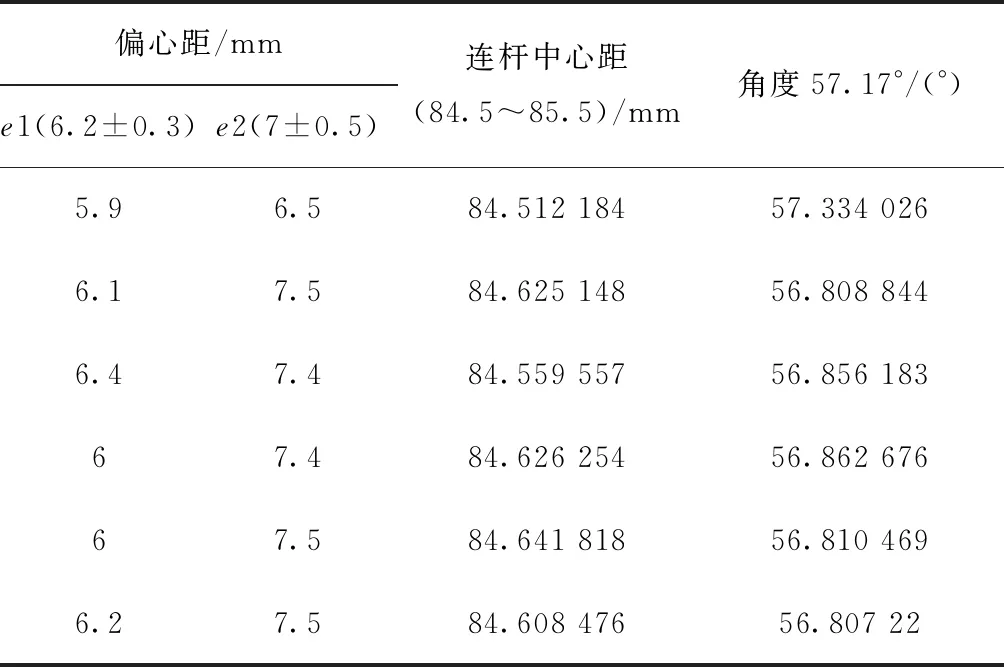
表2 偏心距对连杆中心距、角度57.17°的影响

通过上述分析可知，更换摇臂组件和连杆可快速调节出撑杆所需偏心距，并且变化比例接近1∶0.2∶6，而更换上、下撑杆调节撑杆偏心距效果不佳。值得注意的是：摇臂组件的中心距公差只有0.1 mm，调节范围小，而连杆的公差为1 mm，调节范围大，因此连杆调节偏心距是偏心距调整最快捷且装配效率最高的工艺方法。

3 撑杆在承压试验中的稳定性分析

3.1 撑杆承压试验

可折撑杆及撑杆锁设有微小偏心距，以保证受载时稳定可靠，不因受载变形而开锁。若偏心距值过小，撑杆受压时会因变形或安装误差使偏心距值小于零而开锁；若偏心距值过大，则会引起较大的附加载荷。在起落架放下时，撑杆展开并上锁将主起支柱锁定在放下位置，从而使主支柱能够承受航向和垂向载荷。撑杆连接简图如图5所示。

3.2 撑杆承压试验稳定性分析

撑杆的主要承力件中除撑杆作动筒为弹性组件外，其他均为刚性零件。在承受压载荷时，偏心距e1是依靠偏心距e2进行支撑，而e2是依靠撑杆作动筒锁定的，因此需要考虑撑杆作动筒装配后对e2的支撑力[3-5]。

撑杆作动筒支撑力：

F弹=KX

(1)

式中，K是弹性系数；X是弹簧压缩长度。

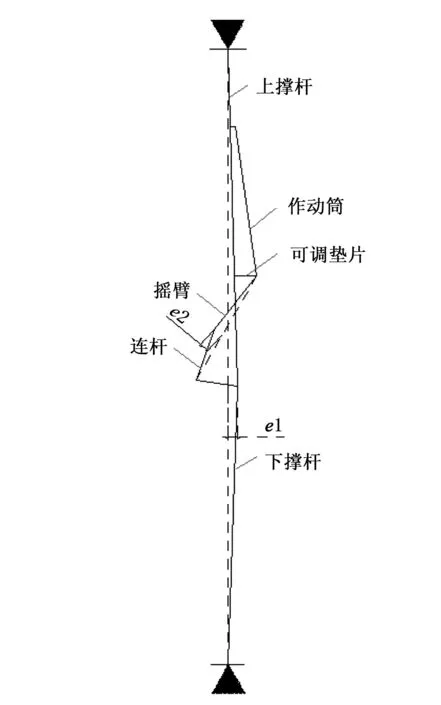
图5 撑杆连接简图

通过式1可知，在弹簧选定后，弹簧的压缩量是决定作动筒支撑力的关键因素。在保证撑杆偏心距e1、e2在(6.2±0.3) mm、(7±0.5) mm范围内进行承压试验来验证产品稳定性。将撑杆放置在曲线机上，保持上撑杆与压力机连接部位不动的情况下，通过压力机油缸上升产生压缩载荷，同时将百分表端头放置在上、下撑杆联接螺栓部位，检测在载荷达到206 kN的过程中，e1变化量≤0.7 mm[6-10]。现将撑杆的稳定性转化为在承压试验中偏心距e1的变化量，可调整作动筒的压缩量>1 mm时观察其对撑杆稳定性的影响，检测偏心距e1变化量(见表3)。

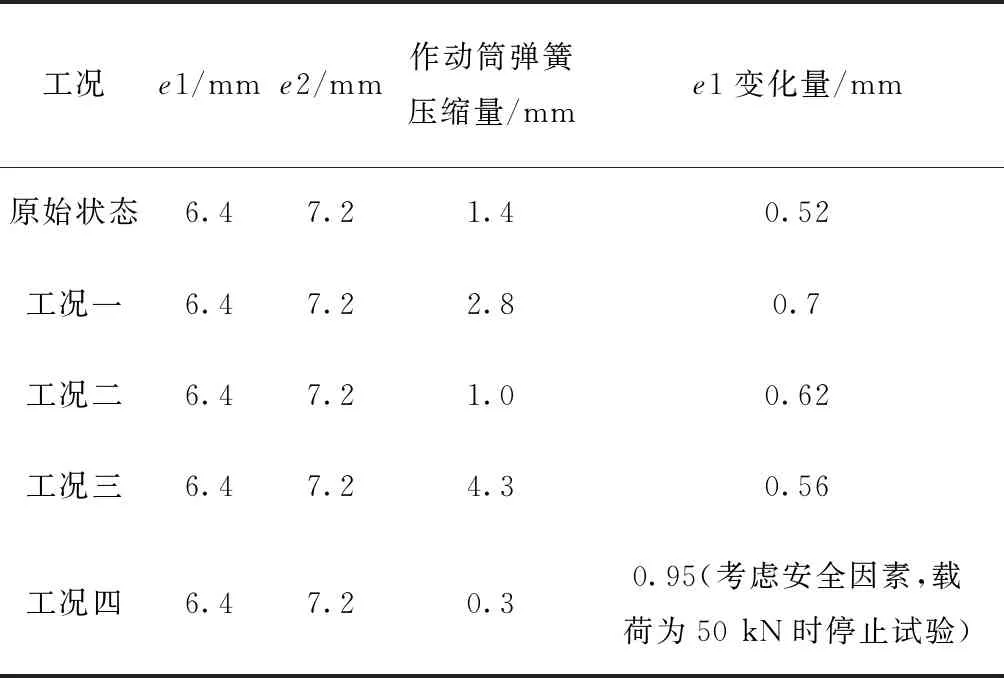
表3 作动筒压缩量在承压试验中的影响

上述4种工况试验数据的线性回归分析如图6所示。由图6可知：P=0.279>0.05，线性关系不明显，即在保证作动筒弹簧存在压缩量的情况下，调整压缩量的大小对e1偏心距变化量没有决定性影响，但撑杆作动筒在较小或无压缩量进行装配时对撑杆稳定性影响较大。

3.3 铰接点位配合间隙对撑杆稳定性的影响

在给定零件材料、几何形状的情况下，组件的装配间隙也是影响偏心距变化量的重要因素。为此，进行了4组工艺试验，通过改变4个关键铰接点(见图3)联接螺栓的外径值，分析e1偏心距变化量。用于试验的螺栓编号为A1、B1、C1、D1，按不同直径分为8组(共32项)，其直径尺寸及组别详见表4。

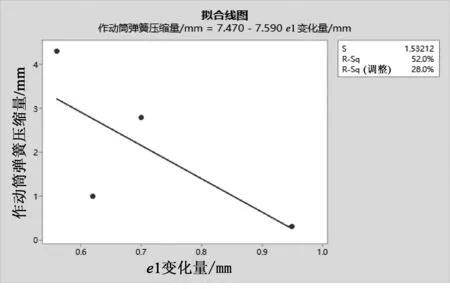
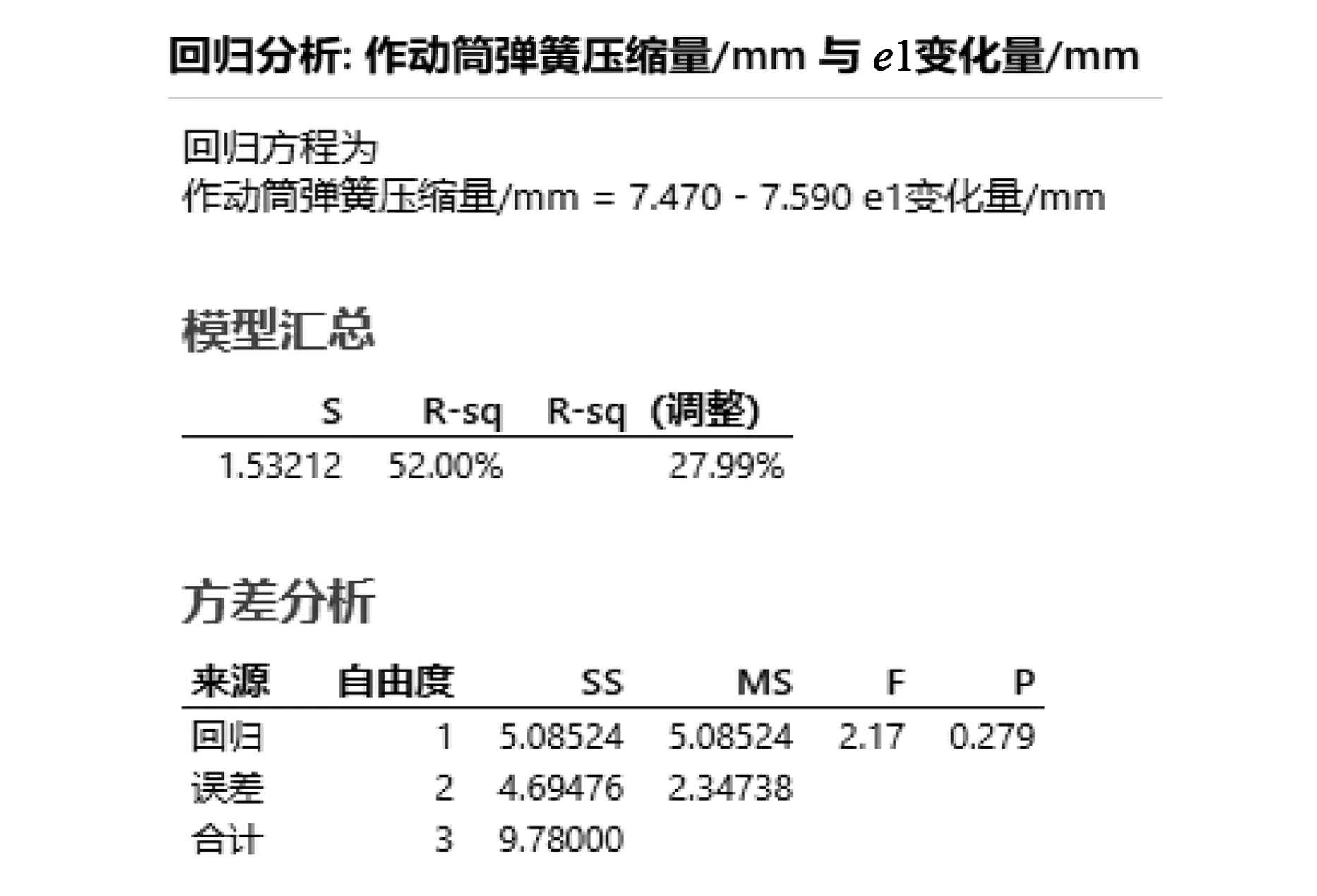
图6 作动筒弹簧压缩量与e1变化量的线性回归分析

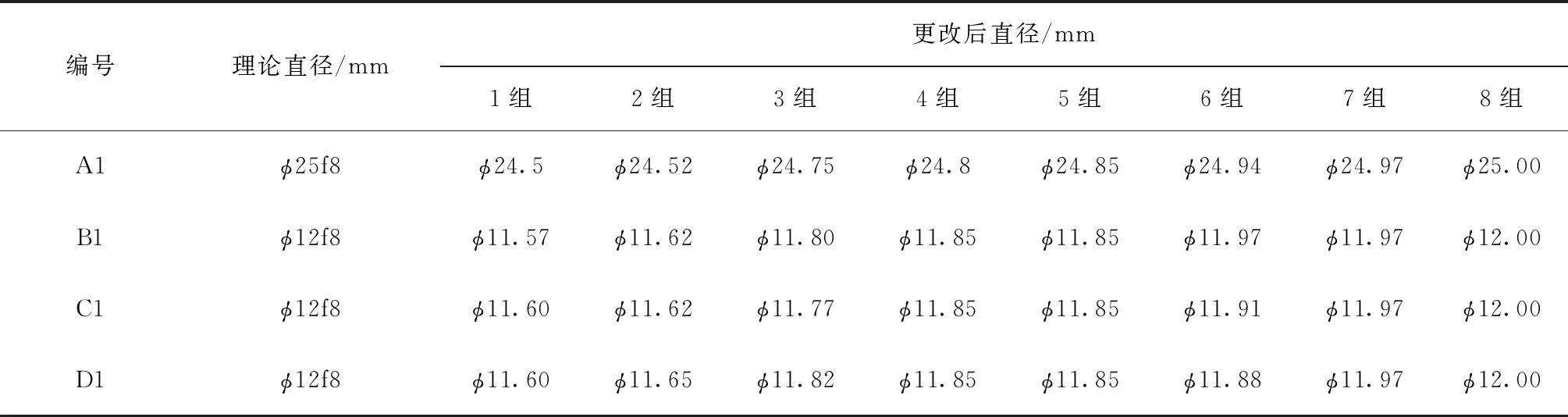
表4 直径尺寸及组别

试验前，通过调整止动垫圈厚度或连杆尺寸，使偏心距满足e1=(6.2±0.3) mm、e2=(7.0±0.5) mm，确保4处铰接点位零件内孔尺寸一致。任意选取表4中8组不同铰接间隙的螺栓进行承压试验，其线性载荷F下的偏心距变化量Δe1见表5。表5中，Δe1为正表示百分表是顺时针转动，偏心距增大；反之偏心距减小。

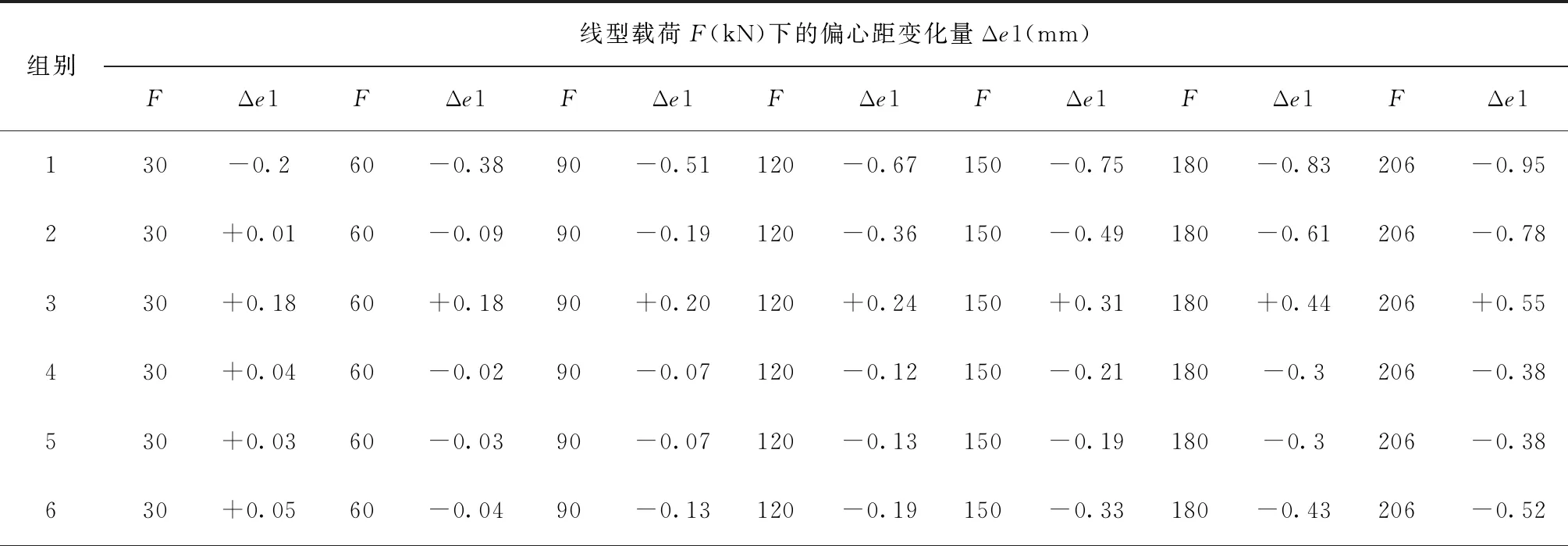
表5 8组不同铰接间隙撑杆承压试验结果

(续表)

8组载荷F与偏心距变化量Δe1一元回归分析如图7所示。由图7可知：P<0.05回归方程显著，偏心距变化量Δe1对载荷F的影响占9.64%，铰接零件配合间隙对撑杆稳定性的影响较为显著，撑杆在受到相同载荷时，间隙越小，撑杆的稳定性就越高。

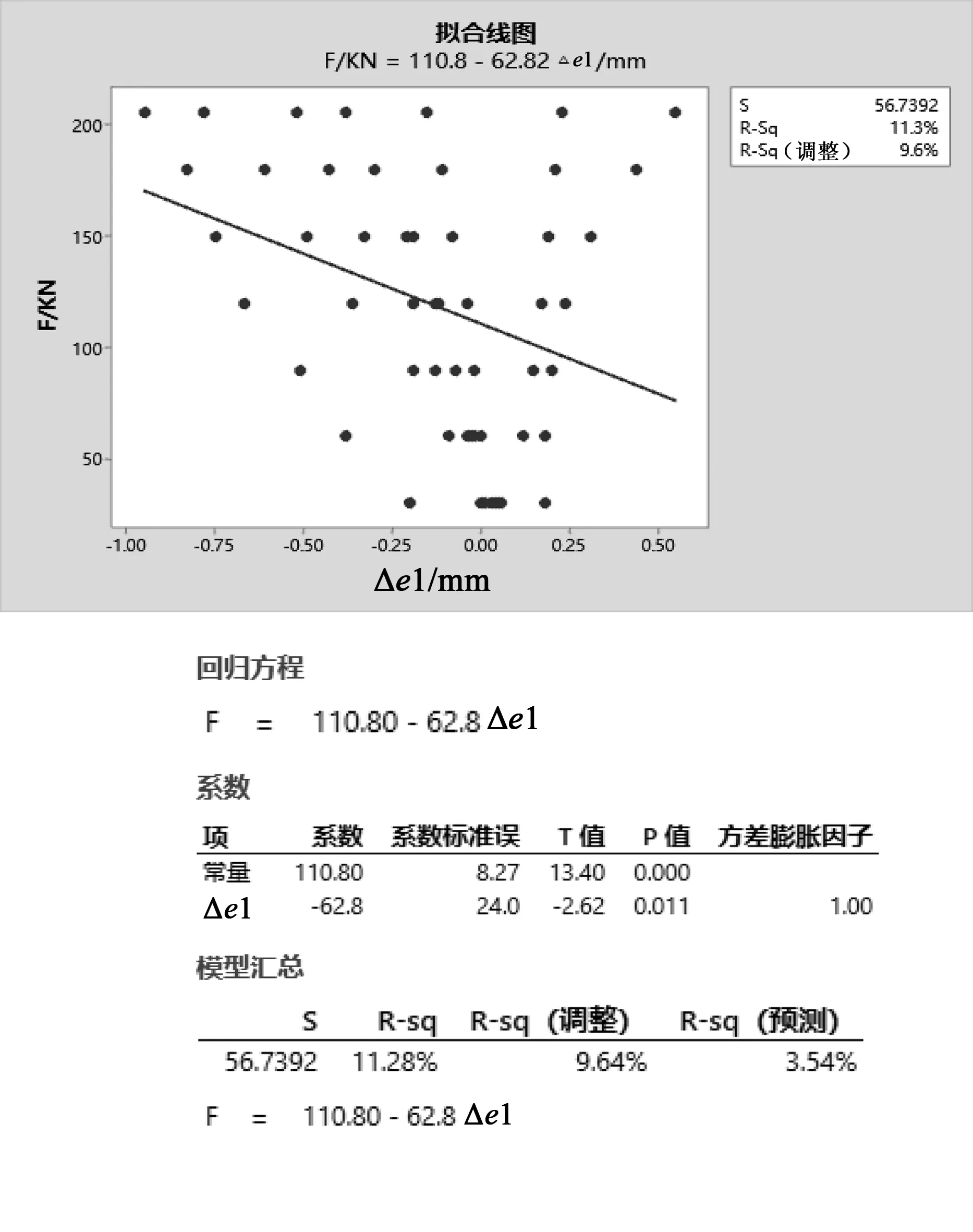
图7 F-Δe1一元线性拟合图与回归方程

4 结语

撑杆稳定性由2项指标决定：第1项指标为依靠上、下撑杆及连杆、摇臂建立起的偏心距e1、e2；第2项为撑杆在承载(停机时承受飞机载荷)时偏心距e1的稳定性指标。通过机构工作原理、稳定性试验分析可知，采用尺寸驱动计算偏心距e1、e2可提高偏心距调节的准确性和高效性。虽然在给定零件材料、几何形状，保证作动筒弹簧压缩量>1 mm的工况下，调整压缩量数值，偏心距变化量无明显变化，但是在实际装配过程中发现，撑杆作动筒在较小或零压缩量的状态下，对撑杆稳定性影响很大。同时，零件间隙对承压稳定性影响较为显著，间隙量越小，撑杆稳定性就越高。