基于CFD方法的溢洪道下游水流数值模拟
2021-04-16徐解刚蒋利俊夏雪峰施建业
徐解刚,蒋利俊,夏雪峰,施建业
(1.宜兴市湖镇水利站,江苏 宜兴 214200;2.宜兴市西渚镇水利站,江苏 宜兴 214200;3.宜兴市芳桥街道水利站,江苏宜兴 214200;4.扬州市勘测设计研究院有限公司,江苏 扬州 225000)
1 引言
溢洪道是最重要的水工建筑物之一,用于防止大坝漫顶,并在洪水期间提供足够的安全性和稳定性。溢洪道设计不当可能导致大坝失效;因此,溢洪道必须经过科学设计,并且在水力上足以验证水流特性。
溢洪道的水流分析是一个重要的工程问题。因此,计算机科学和数值技术的最新发展推动了计算流体力学(CFD)的使用,将其作为实现这一目的的强大工具[1]。计算流体动力学是一种用于解决流体流动问题的数值方法。由于计算流体力学可以提供比物理模型更快、更经济的解决方案,工程师们在验证计算流体力学软件方面研究较为丰富。骆霄等[2]采用Flow-3D对高速水流无压溢洪洞内消能工进行了数值模拟。洪亮等[3]基于Flow-3D 软件对涵洞鱼道进行了三维水流数值模拟。
本文采用计算流体力学软件Flow-3D 对整个溢洪道的水流特性进行研究。此外,通过将结果与实验结果进行比较,对该软件在溢洪道配置方面的能力进行检验。
2 试验模型
3 数字方法论
Flow-3D 是一个强大的计算流体力学软件,能够解决广泛的流体流动问题。它使用有限体积法求解RANS 方程。该软件利用真实流体体积法(VOF 法)计算自由表面运动,并使用面积/体积障碍物表示法(FAVOR)对复杂的几何区域进行建模。在真正的VOF 方法中,使用了一种特殊的平流技术,该技术给出了自由表面的清晰定义,并且不计算空隙或空气区域中的动力学。在分析开始时,定义每个单元中障碍物占据的体积或面积部分,并计算每个单元中的流体分数。流体分数的连续性方程和动量方程使用FAVOR 函数来表示,并且有限体积法或有限差分近似用于每个方程的离散化和求解。
一般的控制质量连续性方程,包括VOF 和FAVOR 变量,可以写成:
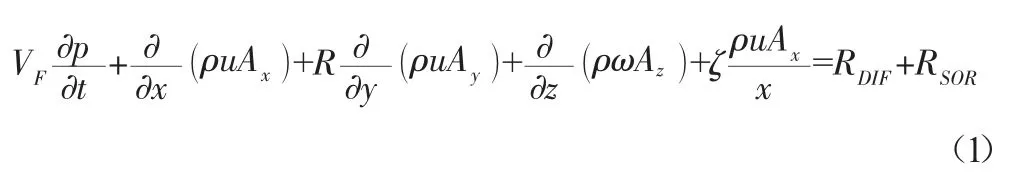
式中:VF是开放流动的分数体积,ρ 是流体密度,RDIF是湍流扩散项,RSOR是质量源。速度分量(u,υ,ω)可以在坐标方向(x,y,z)或(r,θ,z)。Ax、Ay和Az是在x、y和z方向上开放流动的部分区域。
公式(1)右侧的第一项是湍流扩散项:
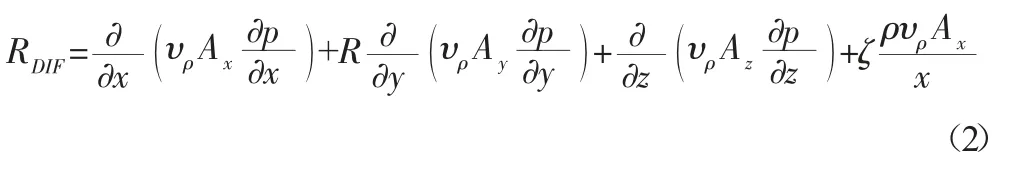
其中系数νρ=Cρμ/ρ,其中μ是动量扩散的系数,Cp是一个常数,其倒数通常被称为湍流施密特数。最后,最后一项,RSOR在公式(1)的右边是一个密度源项,例如,可用于模拟通过多孔障碍物表面的质量注入。在可压缩流动问题中,需要全密度输运方程的解,如公式(1)所述。对于不可压缩流动问题,ρ是常数,公式(1)简化为不可压缩条件:
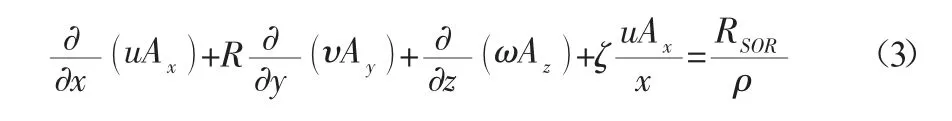
流体速度分量的运动方程(u,υ,ω)在三个坐标方向上,可以写成:
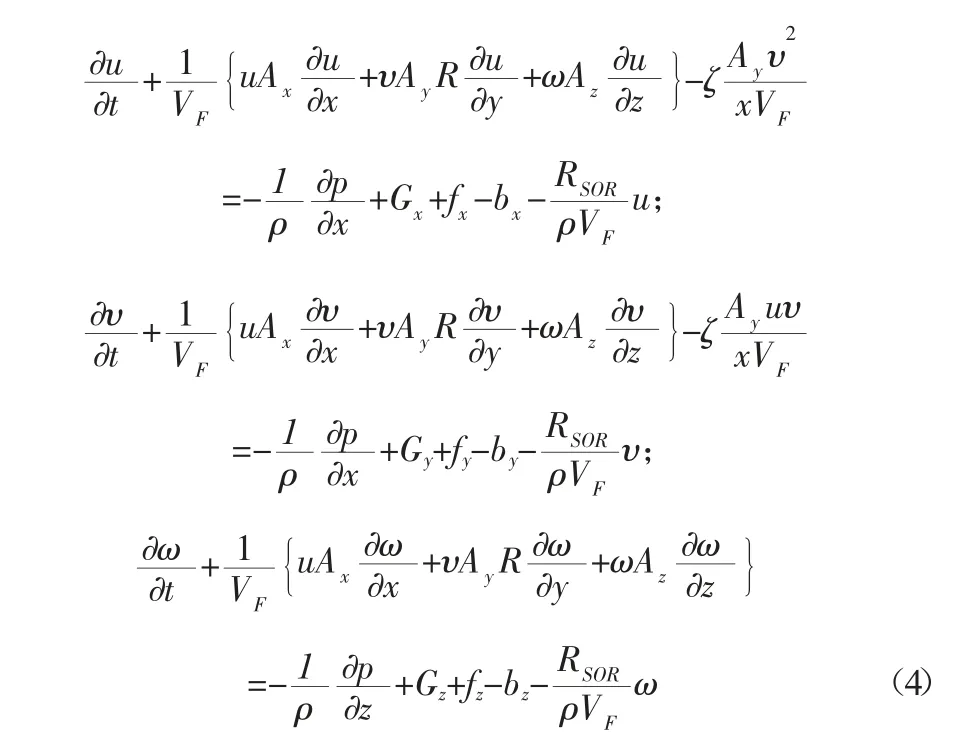
其中(Gx,Gy,Gz)是重力加速度,(fx,fy,fz)是粘性加速度,(bx,by,bz)是多孔介质中的流动损失,最终说明了在由几何成分表示的源处的质量注入。Uw=(uw,υw,ωw)是源分量的速度,Us=(us,υs,ωs)是流体在源头表面相对于源头本身的速度。如前所述,Flow-3D 使用有限差分或有限体积近似对控制方程进行数值求解。流动区域被细分为矩形单元。每个单元格都有相关的因变量的局部平均值。该软件中使用关于时间和空间增量的一阶有限差分近似。即使有限差分网格不均匀,也采取了特殊的预防措施来保持这种精度。此外,二阶精确选项也可用。无论如何,边界条件在任何情况下都至少是一阶精确的。例如,动量方程的有限差分近似的一般形式(公式(4))可以写成:

其中Ri+1/2与坐标系有关,在笛卡尔坐标中等于1。平流、粘性和加速度项有明显的含义。例如,FUX 表示u在x方向的平流通量;VISX是粘性加速度的x分量;BX是垂直于x方向的挡板的流量损失;WSX是x方向的粘性壁加速度,GX包括重力、旋转和一般非惯性加速度。
4 数值模型
采用三维水流软件对油车水库溢洪道上的水流进行模拟。溢洪道的几何图形由Auto-Cad 软件创建,并导出为立体平版(stl)格式。然后,将stl 文件直接导入到Flow-3D 中。计算范围包括溢洪道坝顶前150 m、整个溢洪道结构和挑坎后300 m。此外,在垂直方向的计算域中,考虑了溢洪道顶部上方约50 m 处。RNG 湍流模型是Flow-3D 软件中最精确的模型[4]。
设置合适的边界条件对数值结果是否反映实际情况有重要影响。由于该软件中的流动区域被定义为笛卡尔坐标中的六面体,因此有六个不同的边界需要固定。在这种情况下,需要自由表面流的流量数据。因此,在垂直方向上,顶部边界被设定为大气压,底部边界为边壁。由于这些模拟的目的是模拟具有不同水头水平的溢洪道上的流速,以便与物理模型数据进行比较,因此上游边界被设定为基于溢洪道顶部上的总流体高度的指定压力,而下游边界被设定为流出。值得一提的是,该软件中还有其他几种边界选项可以应用于下游侧。y 方向或垂直于流动方向的边界条件被指定为两侧的壁。图1 显示了在每个方向设置的边界条件。实现尽可能接近实际流场的精确初始条件对模拟时间有非常重要的影响。对于初始条件,在溢洪道的上游和下游指定了矩形区域,认为压力是垂直方向上的流体静力分布。在溢洪道的下游和上游指定了矩形流体区域,其高度与边界处指定的流体高度相同。图2 显示了溢洪道的情况分析的开始。在这种情况下,指定的流体高度为181.2 m,以提供1370 m3/s 的流速。

图1 边界条件

图2 溢洪道情况分析图
通常,每个数值模型都以计算网格或网格开始。它由许多相互连接的单元组成,这些单元将物理空间细分为小体积,每个小体积都有几个相关的节点。节点用于存储未知参数的值,如压力和速度。确定合适的网格尺寸也是任何数值模拟的重要部分。网格大小不仅会影响结果的准确性,还会影响模拟时间。因此,重要的是尽量减少网格的数量,同时包括足够的分辨率,以充分获得几何图形和流动细节的重要特征。本文考虑了四种不同的网格类型。每个网格类型的网格大小和相应的计算时间见表1。每种网格类型的精度与实验结果的比较见图3。结果基于1370 m3/s 流量下的平均流动深度。根据计算结果的准确性和每种网格类型的相应模拟时间,选择第二种网格类型进行其余模拟,并基于该网格尺寸给出数值结果。

表1 网格类型和相应的计算时间

图3 基于平均流动深度的每种网格类型的精度
5 结果分析
通过三维数值模拟,获得了四种不同流量条件下的流动深度、速度和压力等流动特性。结果与水工模型试验结果进行了比较。沿溢洪道的测压管压力值是针对四种不同的流量进行计算的。图4~图7 显示了溢洪道的压力分布。可以看出,数值模型的结果与实验结果有相当好的一致性。对于所有流速,斜槽上的最小压力出现在距离溢洪道顶部140 m 处。斜槽这一部分的压降可能会导致气穴现象,对结构有害。表2 给出了计算的测压压力值和测量的测压压力值之间的差值百分比。可以看出,最大差值为7.97%,数值符合较好。对于所有流速,由数值模型计算并由水力模型测量的平均速度分布见图8~图11。根据结果,我们发现随着流速增加,流速也增加。此外,由于斜槽末端区域的高流速,这些区域可能存在严重至严重气蚀损坏的风险。表3 给出了计算结果和实验结果之间的差异百分比。可以看出,结果之间的最大差异为5.47%,小于6%,计算值与实验结果符合较好。
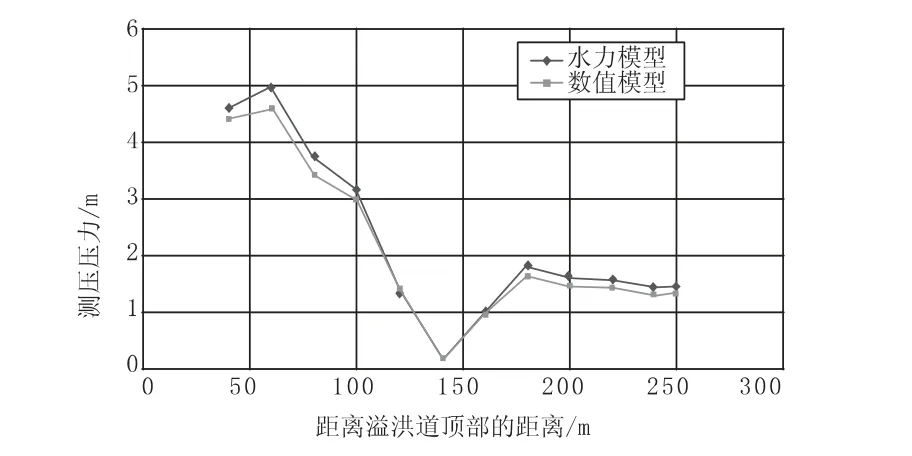
图4 Q=1370 m3/s 时计算和测量的测压压力的比较
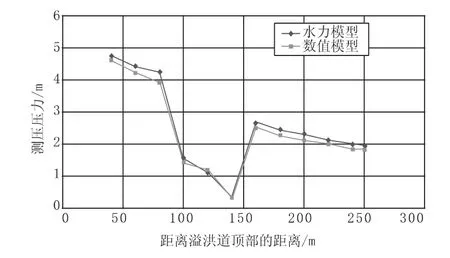
图5 Q=2000 m3/s 时计算压力和测压压力的比较

图6 Q=2500 m3/s 时计算和测量的测压压力的比较

图7 Q=3000 m3/s 时计算压力和测量压力的比较

图8 Q=1370 m3/s 时计算和测量平均流速的比较

图9 Q=2000 m3/s 时计算和测量平均流速的比较

图10 Q=2500 m3/s 时计算和测量平均流速的比较
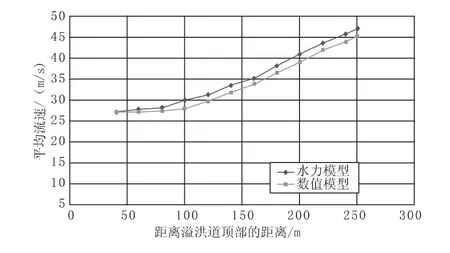
图11 Q=3000 m3/s 时计算和测量平均流速的比较

表2 计算的测压压力和测量的测压压力之差

表3 计算流速和测量流速之差
6 结论
物理测量既昂贵又耗时,数值模拟是分析溢洪道水流的一种方便有效的工具。采用数值模拟可以提供完整流场的详细信息,保证设计的正确性。本研究采用计算流体力学软件Flow-3D 对溢洪道的水流进行了模拟。结果表明,数值结果与实验吻合较好。平均速度值的计算结果和实验结果之间的最大差异为5.47%,测压压力值的最大差异为7.97%。该软件对溢洪道水流数值模拟能力的评估证明是成功的。
