基于浆液稠度时空变化的盾构隧道壁后注浆扩散机制
2021-04-16乔世范檀俊坤郭佳奇张细宝谢济仁喻伟方正
乔世范,檀俊坤,郭佳奇,张细宝,谢济仁,喻伟,方正
(1.中南大学土木工程学院,湖南长沙,410075;2.河南理工大学土木学院,河南焦作,454150;3.中铁五局集团电务工程有限责任公司,湖南长沙,410006;4.中铁南方投资集团有限公司,广东深圳,518052)
盾构法因具有施工效率高、安全性好以及对周边环境影响小等优点,被广泛应用于水利管廊和地铁隧道等开挖工程中[1-2]。在盾构施工中,盾构刀盘及盾体半径通常大于拼装管片半径,以避免卡机现象发生。由此,盾构施工拼装后的管片与岩体之间形成一个可达10 cm 左右的间隙[3],造成隧道围岩土体松落。为稳定隧道管片位置、确保隧道工程质量,通常通过管片的注浆孔向隧道外围土体注入水泥浆液,削减地层应力释放和地层变形对隧道管片稳定性产生的不利性影响[4-5]。在隧道管片壁后注浆加固过程中,注浆浆液会对管片产生向内挤压力,随着浆液进行,浆液压力上升到一定程度造成隧道管片整体或局部损毁[6]。因此,盾构隧道壁后注浆浆液扩散半径及管片承压等问题对盾构壁后注浆具有十分重要的作用[7]。
现阶段,许多学者通过现场监测、模型试验、理论分析及数值模拟等方式研究隧道壁后注浆浆液的扩散形式、管片承压及浆液压力分布等[8-11]。YE 等[12]对充填注浆的扩散机理进行理论研究,建立考虑回填注浆渗透效应的半球面扩散模型,发现注浆压力分布规律,并定义有效注浆扩散半径的概念;BEZUIJEN等[13]通过隧道壁后注浆现场试验,发现浆体压力呈现上部小、下部大的特征;随时间不断推移,注浆浆液的扩散速度与浆体锋面压力均逐步下降,最终浆液扩散半径不再增加,浆液锋面压力与地下水压力趋于相等。KOYAMA[14]通过大型注浆模型试验,发现当注浆压力较小时,土体空隙难以充分填充,充填效果不理想,注浆压力过大会造成砂层密实处土体局部破坏;袁小会等[15]通过实际工程以及室内试验,深入研究宾汉流体在盾尾间隙注浆过程压力分布及浆液的流变性,推导出了盾尾空隙过程中注浆压力的传递公式,并用Sophia 隧道的监测结果验证了注浆压力分布模型的合理性;KASPER等[16]对盾构壁后浆体压力分布形式进行数值模拟,指出壁后注浆压力对上部土体变形和管片受压变形起到决定性作用。
以往研究多基于注浆浆液在扩散区域内,假定不同位置浆液稠度在同一时刻稠度相同,浆液稠度随时间同步变化。因在水泥注浆过程中忽略浆液稠度空间分布不均匀性,计算得到的浆液压力往往较实际浆液压力偏高。本文基于稠度时变性幂律本构模型,首先,研究水泥浆液在净水条件下盾构壁后注浆浆液扩散变化过程;其次,建立考虑浆液稠度时间及空间变换的半球面扩散模型,并推导隧道壁后注浆浆液稠度及浆液压力时空分布方程;最后,探讨公式的适用范围及各种参数取值方式,分析浆液特性和注浆参数等主要因素对隧道壁后注浆浆液扩散半径的影响,并针对考虑与不考虑浆液稠度空间不均匀性所得结果进行比较,验证考虑稠度空间不均匀性的必要性。
1 水泥浆液稠度试验
盾构隧道在臂后注浆过程中水泥浆液保持流动状态,因此,确定浆液流动类型及浆液性质是建立壁后注浆扩散模型的首要条件。基于此,本文对水泥浆液稠度随时间推移的变化规律进行试验研究。
1.1 试验设备及试验材料
试验采用水泥为广东某厂产的32.5R普通硅酸盐水泥,水泥性能满足文献[17]规定。试验设备包括电子称、量筒、温度测量仪、计时器、恒温水箱、旋转型黏度计和搅拌容器等。
1.2 试验设计及过程
根据文献[18]规定,普通硅酸盐水泥初凝时间应大于45 min,据此,本试验研究水泥浆液搅拌完成40 min 内稠度随时间变化的规律。本稠度时变性试验中的水灰比分别选取0.50,0.60和0.70。试验过程如下:
1)将水倒入恒温水箱,水温控制在20 ℃;
2)将水泥放置电子称上进行称质量;
3)使用量筒量从恒温箱内量取适量温水,将水泥倒入搅拌容器,然后将量取好的温水倒入容器内进行搅拌,搅拌先快后慢,分别搅拌2 min,取出搅拌好的浆液倒置5个试验杯,记录时间;
4)将试验杯放置旋转黏度计下,由低到高调节旋转黏度计转速,得到不同配比水泥浆液的流变曲线,所得流变曲线的斜率即为水泥浆液的黏度;
5)每5 min测量1次浆液稠度。
水泥浆液稠度流变曲线如图1所示,由图1知:水泥浆液稠度流变曲线通过原点,水泥浆液的剪切应力随剪切速率增大呈现非线性增加,剪切应力的增大速率随剪切速率增加而减小,符合幂律流体特征。采用幂律方程拟合试验结果,浆液幂律方程的拟合平方差R2均在0.98 以上,拟合所得流动指数n(见表1)小于1,水灰比为0.5~0.7的水泥浆液为剪切稀化流体,表观黏度函数为幂律形式[19],表示为

式中:τ为剪切应力,Pa;c为幂律流体黏度系数,Pa·s;γ为浆液剪切速率,s-1,γ=-dv/dr;v为流速;n流变指数。
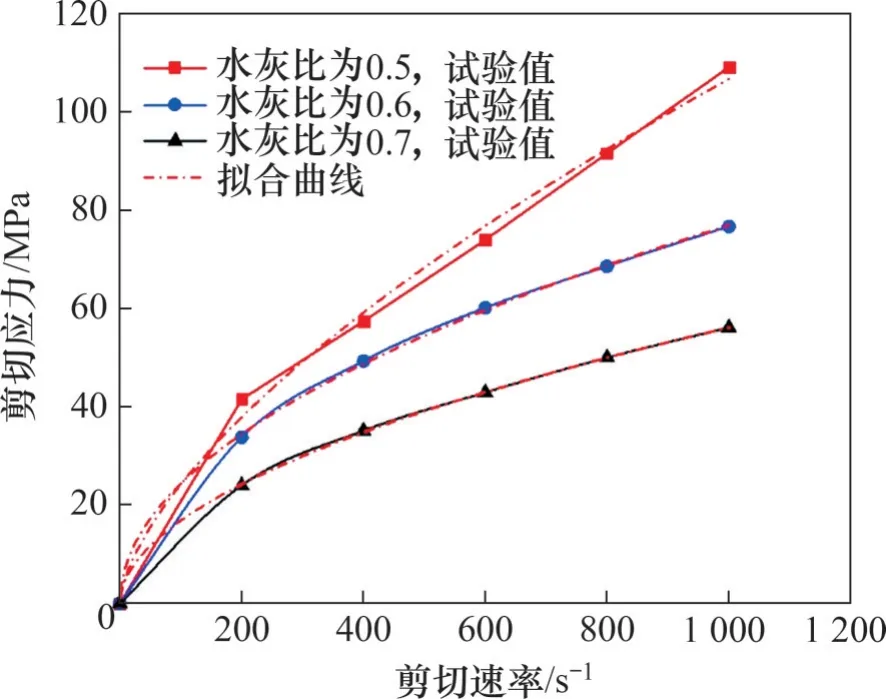
图1 水泥浆液稠度流变曲线Fig.1 Rheological curve of cement slurry consistency
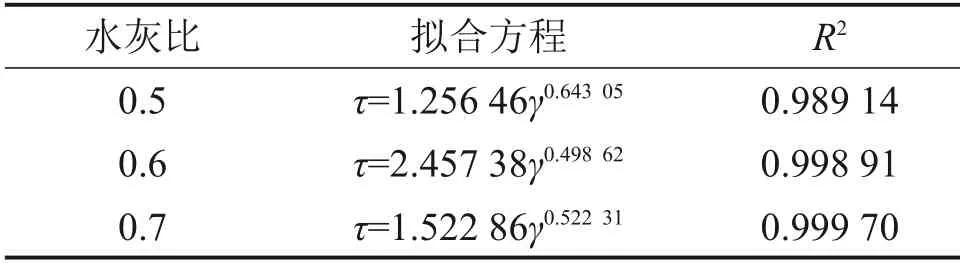
表1 水泥浆液幂律方程拟合Table 1 Power law equation fitting of cement slurry
1.3 试验结果
根据水泥浆液流变曲线,可测得浆液在不同时间的稠度,如图2所示。由图2可知:水泥浆液稠度随水灰比增大而减小;水灰比为0.5的浆液对应的浆液初始稠度约为水灰比为0.6 及0.7 的浆液初始稠度的2倍;各种水灰比黏度均随时间大幅度增加,并随时间延长,水灰比为0.5的浆液稠度增速明显高于水灰比为0.6 与0.7 的浆液稠度增速,水泥浆液稠度与时间的关系曲线基本符合自然对数关系,其流体稠度时变关系可表示为

式中:c(t)为水泥浆液稠度时变函数;c0为水泥浆液初始稠度,Pa·s;λ为水泥浆液稠度时变系数;t为水泥浆液注浆时间,s。
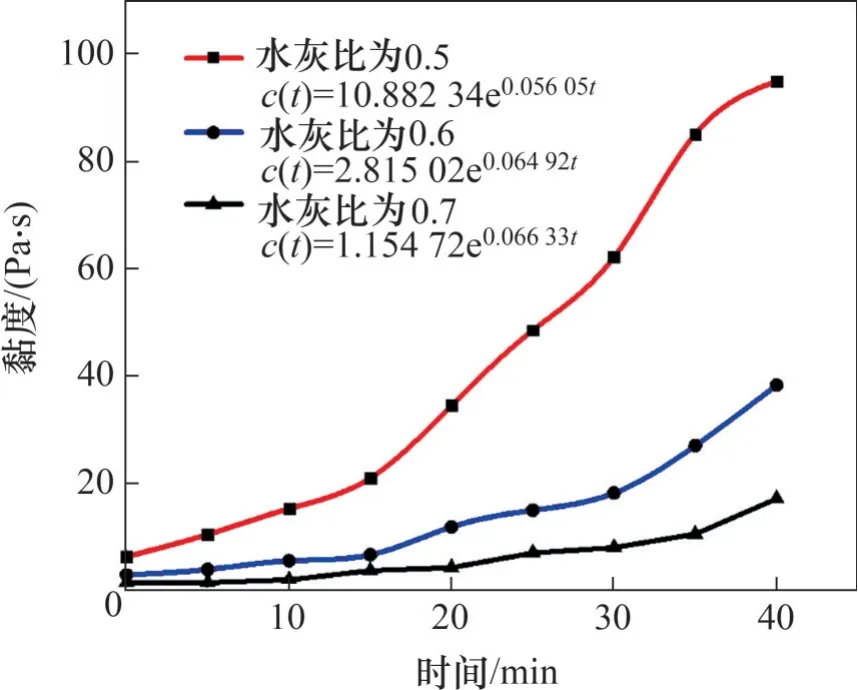
图2 水泥浆液黏度与注浆时间的关系Fig.2 Relationship between viscosity of cement slurry and grouting time
2 幂律型浆液扩散模型
2.1 基本假设
1)浆液和被注介质是不可压缩、均匀的各向同性材料;被注介质骨架为刚体,在注浆过程中浆液的渗透性不发生改变,空隙的几何尺寸不发生变形。
2)浆液扩散方式为完全驱替扩散,不考虑浆液水截面处水对浆液的稀释作用。
3)在注浆过程中,注浆速度保持恒定,忽略重力影响,浆液在被注入介质以半球面扩散,在渗透范围内浆液延注浆孔周围扩散。
4)由于盾构段的开挖半径远大于柱体半径,忽略盾构开挖截面曲率,将管片外壁与盾构开挖内壁均为平面。
5)浆液流速较小,流态为层流。
2.2 浆液稠度时空分布
在注浆速率恒定情况下,注浆机上出浆口与管片注浆孔距离一定,则浆液质点由出浆口到达注浆孔经历时间一致,因此,浆液流至注浆孔处的稠度相同。可认为,浆液进入隧道管片壁的时刻为浆液初始稠度开始增长的起点,随着壁后注浆工程的不断进行,浆液质点持续向前推移,所有浆液质点到达相同位置所需的注浆时间一致。图3所示为假定浆液以注浆孔为球心向外扩散的浆液沿注浆孔以半球面扩散模型。
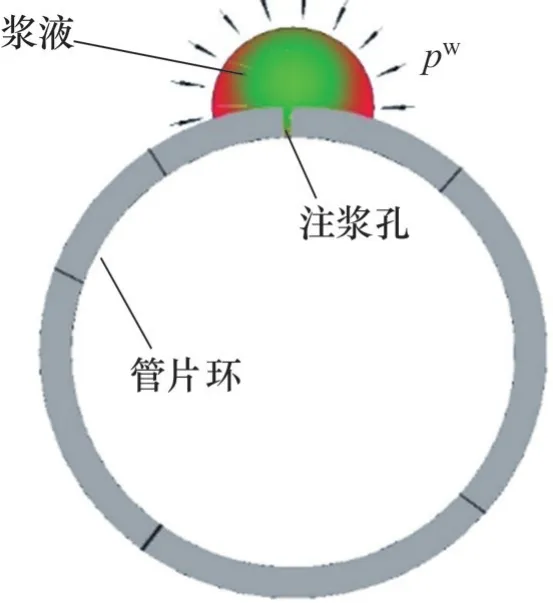
图3 隧道壁后注浆半球面扩散模型Fig.3 Grouting hemispherical slurry diffusion model after shield wall
根据质量守恒定理可知,水泥浆液注入量与隧道壁后浆液扩散量一致,注浆时间与扩散半径关系可表示为
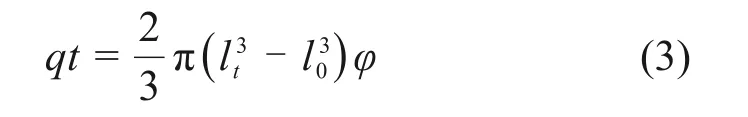
式中:q为注浆速率;l0为注浆孔半径;lt为t时刻注浆球体扩散半径;φ被注入介质的空隙率。
由于注浆孔尺寸远远小于注浆扩散区,因此,忽略注浆空半径l0长度,对式(3)进行恒等变换,可得到浆液扩散半径lt为

在稠度时空分布分析中,定义水泥浆液质点从注浆孔流至隧道壁后的时间ts和浆液质点的稠度增长时间tg这2个时间概念。隧道壁后注浆速率恒定,浆液稠度增长时间以质点从注浆孔到达隧道壁后时刻ts为始点,以水泥注浆时间t为终点[9],则浆液质点的稠度增长时间tg为

浆液扩散的本构方程以浆液质点随时间运动作为描述对象,对于浆液质点,浆液稠度只受时间影响。对于整个浆液动态扩散过程,浆液质点从注浆孔进入隧道壁后,水泥浆液稠度以初始值为起始值,随着扩散时间增加而不断增大。浆液质点随着注浆过程而不断向前移动,但到达不同位置所需要的时间不同,导致不同位置的浆液质点稠度增长时间不同,从而导致不同位置的浆液稠度不同。
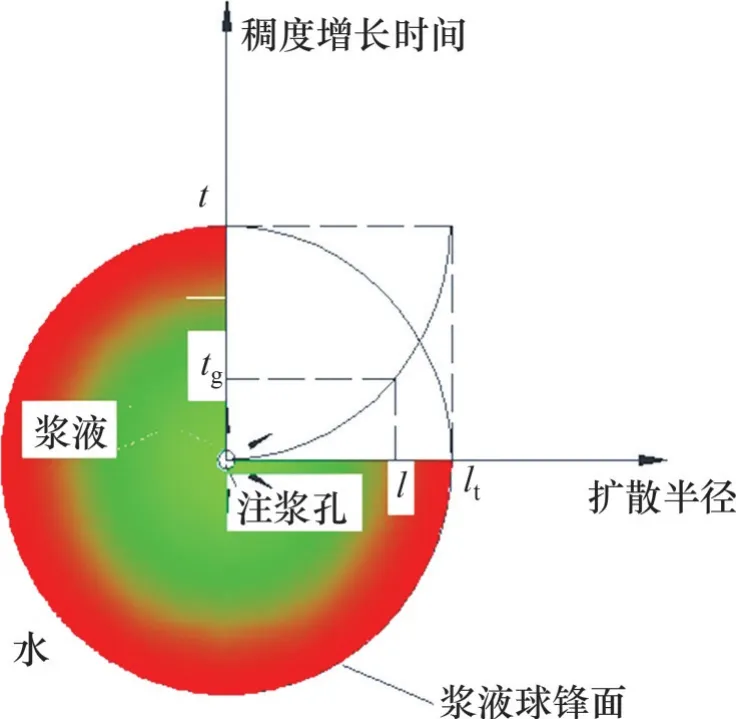
图4 稠度增长时间变化示意图Fig.4 Schematic diagram of growth time of slurry viscosity
浆液质点流入隧道壁后时,t=tg,可知浆液稠度增长时间tg=0 s。因浆液稠度增长时间与浆液扩散空间位置具有一一对应关系,并满足0≤tg≤t的条件,根据质量守恒定理,浆液扩散区内浆液质点距离注浆孔中心位置关系如下:
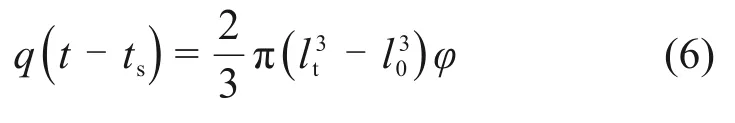
由于注浆孔半径l0远小于注浆扩散半径,忽略注浆孔半径l0,将式(5)代入式(6),可得浆液扩散半径l与其所对应稠度增长时间为

由于注入浆液只在扩散区内进行,浆液质点位置与注浆孔中心点距离均小于浆液半球面扩散半径lt,式(7)应满足以下关系:
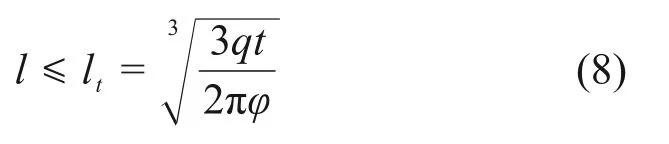
由式(7)可知,浆液稠度增长时间tg与浆液质点到注浆孔中心点的距离l相对应。则l处浆液稠度在注浆时间t时为

将式(7)和(8)代入式(9)得浆液扩散区稠度时空分布方程:
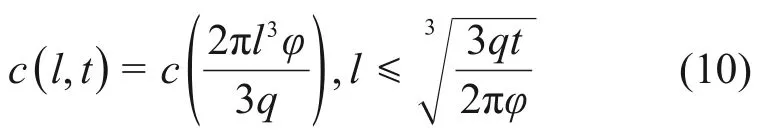
在式(10)中,注浆时间t没有出现在等号右端,由此可知,在注浆速率恒定时,浆液质点的空间位置对浆液稠度有决定作用,浆液扩散半径受注浆时间影响。
2.3 浆液扩散运动方程
假定浆液被注入介质渗流通道做层流运动,地层毛细管均匀分布,并符合均匀毛细管理论,其填充介质毛细管直径取r0,取一段与毛细管同轴的圆柱形微元体(l为长度,r为半径,p为微元体单位面积上所受压力),忽略重力影响,幂律流体毛细管流动示意图如图5所示。
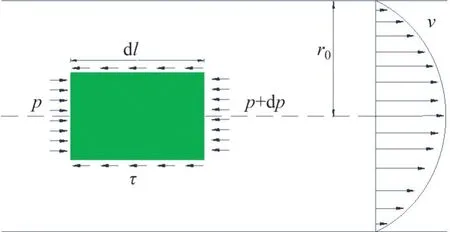
图5 幂律流体毛细管流动示意图Fig.5 Schematic diagram of capillary flow of power law fluid
在不考虑重力的情况下,流体柱受力满足以下平衡关系:
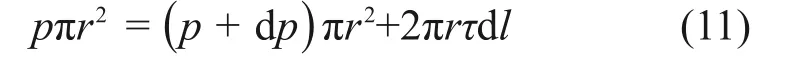
式中:p与p+dp分别为微元流体柱段dl的左端压力与右端压力;τ为微元流体柱面剪应力。
由式(11)推出流体外表面所受剪应力为

式(12)表明剪切应力τ与毛细管内径径向距离呈正比,在管壁附近切应力最大,管中心线附近切应力很小。
将式(12)代入幂律流体的基本流变方程(即式(1)),可得
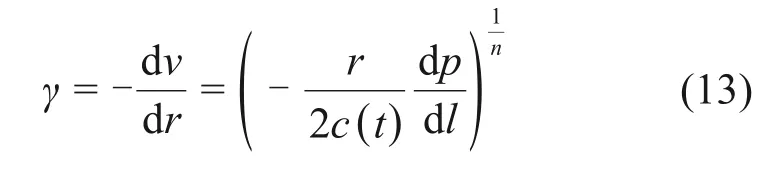
对式(13)进行分离变量积分,并将位于圆边边缘r=r0时流体流速v=0的边界条件代入,得幂律浆液在圆管速度关系式:
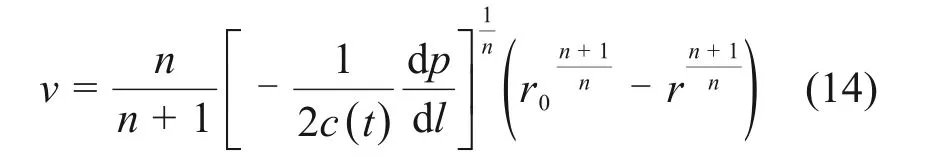
由图5可见:毛细管沿管轴任意剖面内的流体质点速度呈现抛物线状,其单个毛细管单位时间流量q0为剪切区(0≤r≤r0)流量的总和。
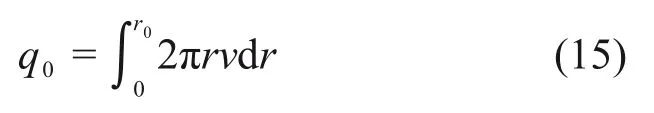
将式(14)代入式(15)并进行整理可得:
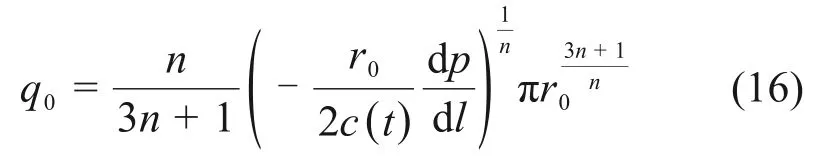
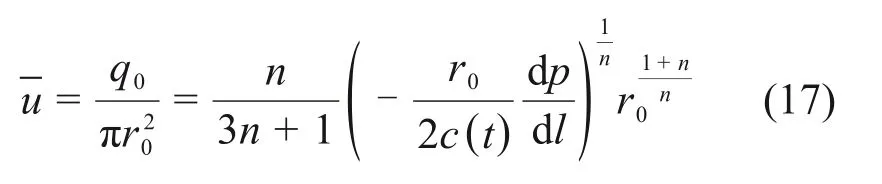
利用Dupuit-Forchheimer 关系式[20],将流体实际质点平均速度转化为渗流速度,得到幂律型浆液在被注介质中运动任意时刻的平均渗流速度为
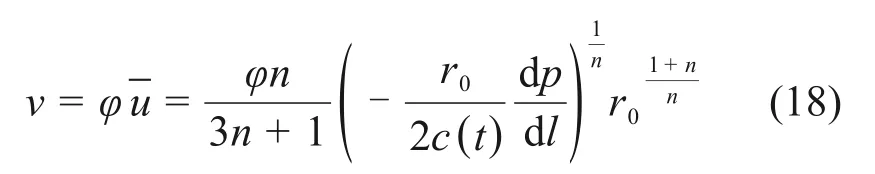
2.4 浆液扩散区内压力时空分布
幂律型注浆过程中单位时间注浆量q为
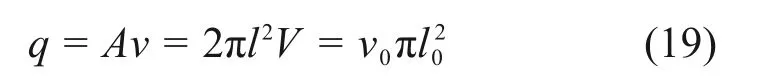
式中:A为任意时刻的半球面浆液的外表面积。将式(10)与(18)代入式(19)可得

对式(20)进行恒等量变换,可得浆液扩散区的压力梯度:
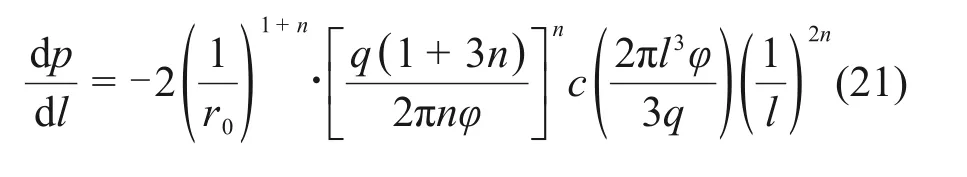
对式(21)在(l0,l)范围内进行积分运算,并将l=l0时,p=p0的注浆边界条件代入,可得到浆液扩散区内任一半径l位置的浆液压力:
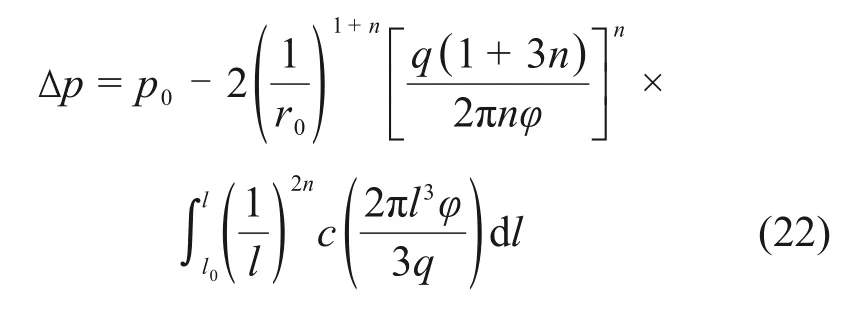
令l=l1时,p=pw,代入式(22),可得时空变化方程:
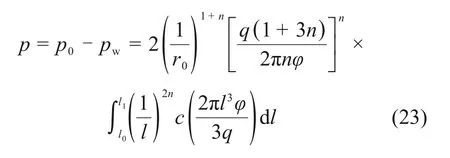
其中:pw是注浆孔位置处的地下水压力。
将幂律浆液稠度时间函数方程(即式(2))化为可解答的压力空间分布方程,采用的稠度时间函数为
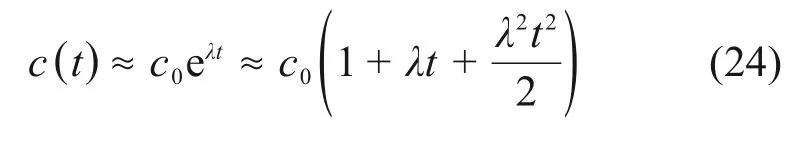
将式(24)代入式(22)和(23),可得任意半径l处的浆液压力:
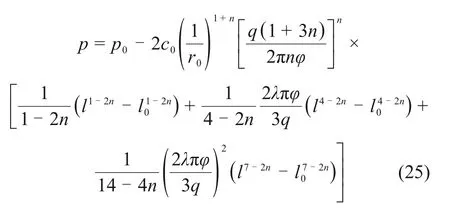
注浆压力差Δp与扩散半径的关系为
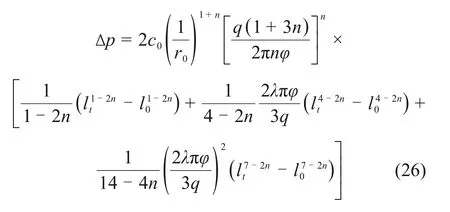
幂律型水泥浆液对管片产生的压力Fg为
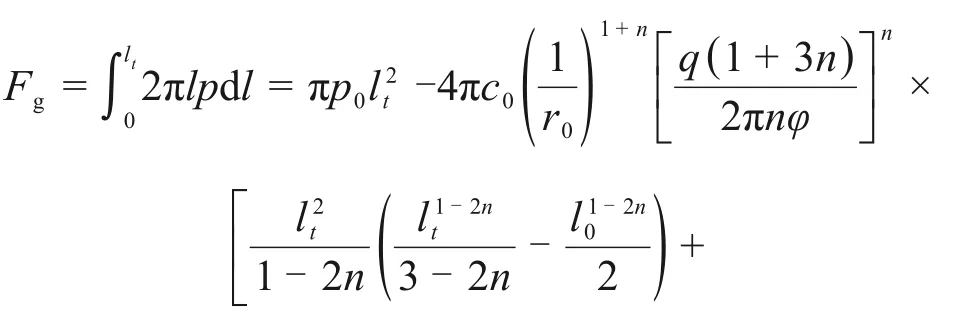
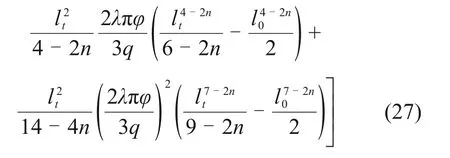
将式(4)代入式(26),可得注浆压力与注浆时间的关系:
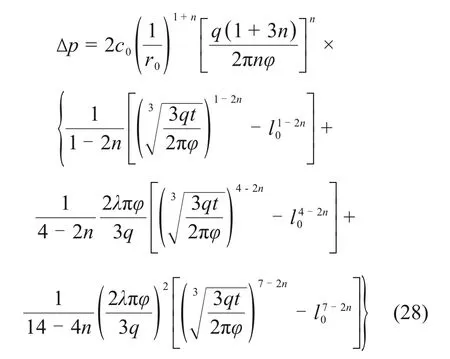
2.5 不考虑浆液分布不均匀性
忽略浆液稠度空间分布不均匀,则浆液质点的稠度只注浆时间有关,与浆液质点所处位无关,由此得任一扩散半径l处的注浆浆液压力:
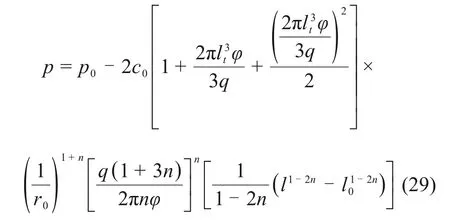
注浆压力差Δp与扩散半径的关系为

幂律型水泥浆液对管片的压力为
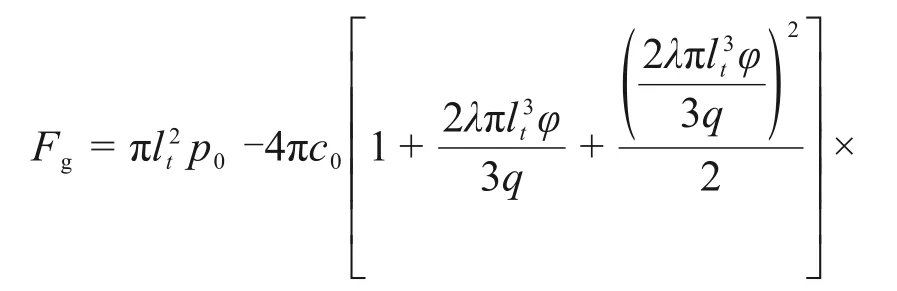
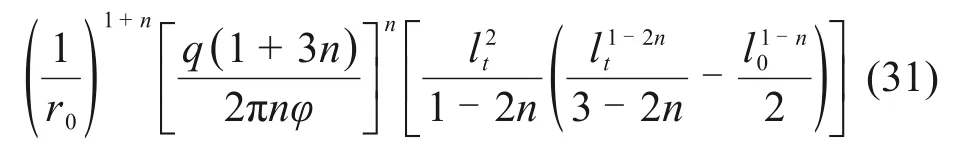
将式(4)代入式(30),可得注浆压力差与注浆时间的关系:
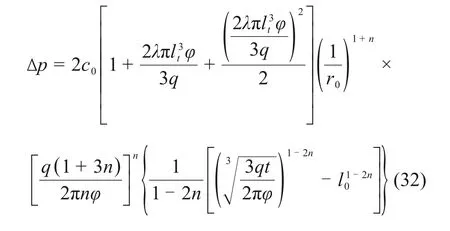
3 参数确定方式及公式适用范围
3.1 参数确定方式
时变性幂律流体渗透扩散模型计算式中的参数,通过以下方式进行确定:
1)注浆孔半径l0可采用卡尺等测量工具多次测定取平均值;
2)可在注浆管端头附近安装压力表,以获得注浆孔压力P0;
3)水泥浆液的初始稠度系数c0、流变指数n及时变指数λ可依据已有的幂律型水泥浆液的稠度时变性研究成果获取[21],或采用室内浆浆液稠度时变试验获取,对试验结果进行线性或非线性回归而得。
4)被填充材料的孔隙率φ为被填充材料的孔隙体积于总体积之比,可由下式计算得出:
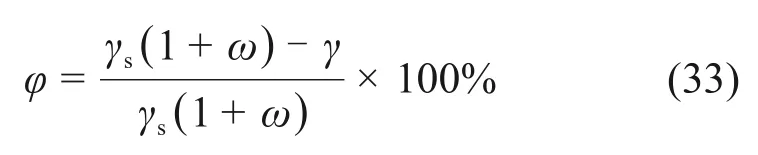
式中:ω为被注入介质的含水率;γ为被注入介质天然容重,kN/m3;γs为被注入介质颗粒容重,kN/m3,以上参数可以通过土工试验确定。毛细管半径r0可通过下式计算:

式中:K为水在被注入介质中的渗透系数。K依据K=kμw/(ρwg)计算求出。不同温度下水的密度ρw及水的黏度μw可通过查阅文献[22]获得。
3.2 公式适用范围
上述公式是基于层流状态下进行的推导,不适用于紊流流体。依据文献[23],可利用Z对圆管中幂律流体对层流和紊流进行划分:当Z大于808时,浆液流体为层流运动;当Z小于808时,浆液流体为紊流运动。以层流稳定理论为基础,认为浆液由层流状态过渡到紊流状态时,紊流的漩涡不同时发生在整个管断面,Z计算式如下:
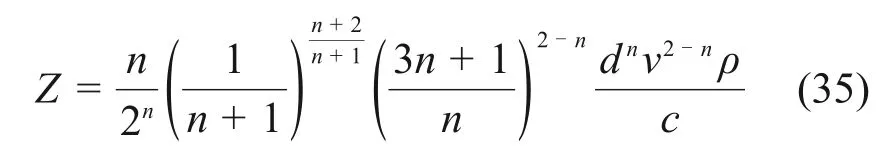
式中:ρ为流体密度;d为圆管直径。
当浆液为牛顿流体时,即流变指数n=1,Z=0.384 9Re,Re为流体雷诺数,当雷诺数大于2 100,流体为紊流型流体;当雷诺数小于2 100时,流体为层流流体。将临界值2 100 代入式(35)可得Z为808,即可用Z=808 为界判断浆液的流态。由于流体在地层中的流动状态不易判断,因此,采用上述方法查明盾构隧道壁后注浆浆液流态难度较大,依据文献[24],在注浆压力不大时,注浆浆液在地层中的渗透速率与浆液的水灰比有关。当水灰比为0.5~0.7,0.8~1.0 和2.0~10.0 时,水泥浆液分别为幂律流体、宾汉流体和牛顿流体。由此可知,上述公式适用于水灰比为0.5~0.7的范围。
4 算例分析
以某城市轨道交通线隧道壁后注浆形式为例进行计算。经室内试验测定,土体孔隙率φ为35%,渗透系数k为0.089 4 m/s。为保证浆液具有长期稳定性、流动性及适当的初凝时间,选用32.5普通硅酸盐水泥,水灰比分别为0.5,0.6 和0.7,注浆孔半径l0为1.4 cm,注浆速度为10 L/min,注浆附近地下水压力pw为0 Pa,地下水温度为20°C,水的黏度uw为1.01×10-3N·s/m2[25]。
4.1 注浆渗透扩散区稠度时空分布比较
由式(3)可得t=90 s 时浆液扩散半径lt=0.25 m,将相关参数代入式(10)与式(24),可得水泥浆液扩散区(l∈[0,lt])内的稠度空间分布曲线如图6所示。
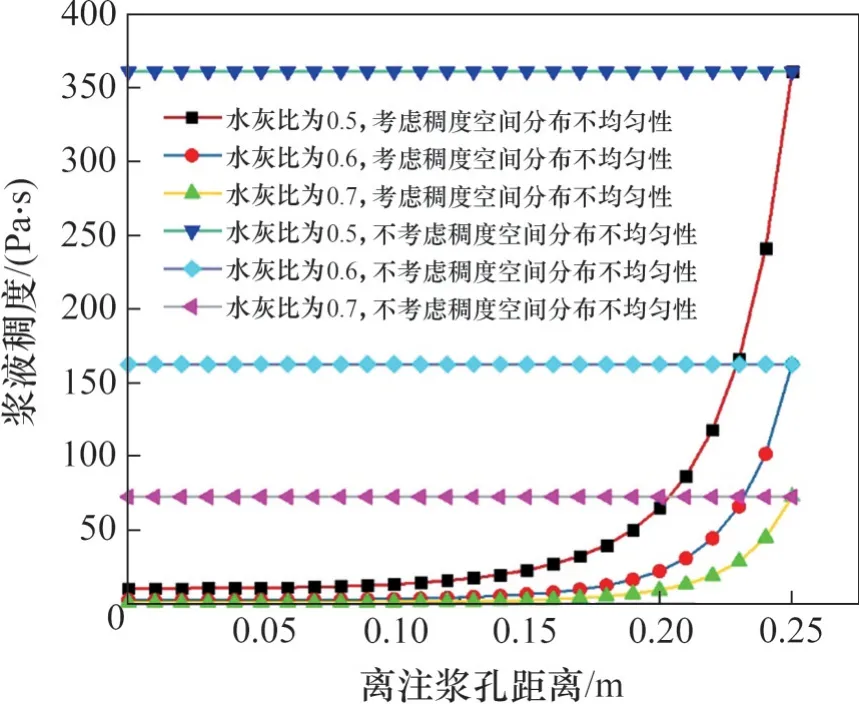
图6 浆液稠度空间分布曲线Fig.6 Spatial distribution curves of slurry consistency
由图6可知:考虑黏度空间不均匀性时,浆液空间分布曲线初期表现缓慢上升;随着离注浆孔中心位置距离增加到一定程度(约0.17 m后),浆液稠度增加速度迅速提高,表明浆液离注浆孔距离越远,稠度越大,且稠度随距离增加速率迅速增加,浆液稠度时间函数与浆液稠度空间分布一一对应;考虑与不考虑稠度空间分布不均匀性的2种浆液扩散锋面处的表观稠度相同,其原因在于水泥浆液注浆时间和浆液扩散锋面处浆液增长时间相等;在注浆孔距离0~0.25 m 扩散区内,水灰比分别为0.5,0.6 和0.7 的浆液稠度空间分布曲线由上至下依次排列,且曲率由大到小依次分布;水泥浆液初始稠度随着水灰比减小而增大,其稠度差随离注浆中心距离增大而增大,不同浆液水灰比稠度增长速率的差值随浆液质点扩散距离增加而增大。
4.2 注浆压力比较
将隧道壁后注浆相关参数代入式(28)和(32),得到壁后注浆压力与时间推移变化关系,见图7。
由图7可知:在盾构隧道壁后注浆初期,考虑浆液与不考虑稠度分布不均匀性这2种情况下的壁后注浆压力差值较小,水灰比对不考虑稠度空间分布不均匀性影响不大,对考虑浆液稠度时空分布不均匀性影响明显,具体表现为随浆液稠度增大,浆液压力增长速率减小;随着注浆时间增加,不考虑稠度空间不均匀性所得注浆压力明显较高,且两者之间的差值不断扩大,在10 min 时两者差值可达60 倍以上。这表明对于隧道壁后水泥注浆工程,充分考虑浆液空间分布不均匀性十分必要。
4.3 注浆终压与扩散半径
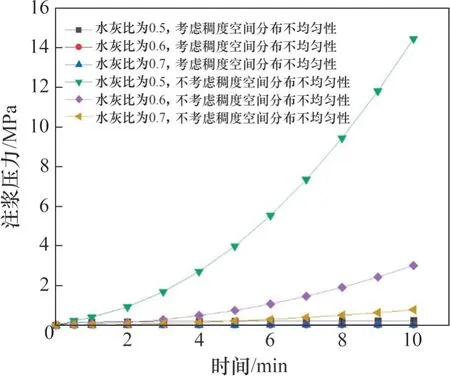
图7 注浆压力随时间变化曲线Fig.7 Curves of grouting pressure with time
浆液扩散半径以注浆结束标准,将参数代入式(26)和(30),得到水泥浆液盾构壁后注浆扩散半径与注浆终压的关系,如图8所示。
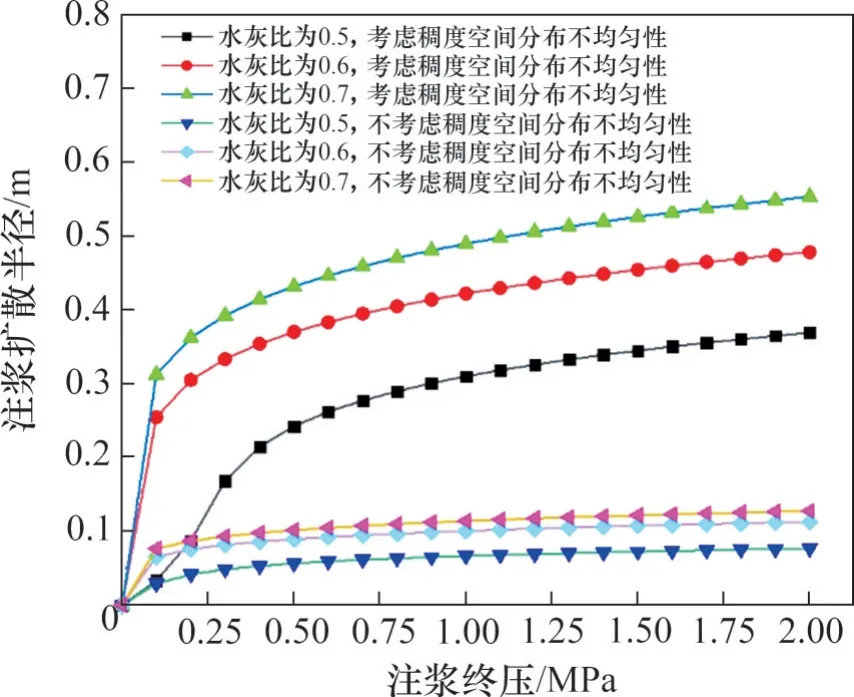
图8 浆液扩散半径与终压变化关系Fig.8 Relationship between slurry diffusion radius and final pressure
由图8可知:
1)随注浆终压增大,浆液扩散半径增速表现出明显的阶段性。在注浆终压较小时,随注浆终压增大,水泥浆液扩散半径扩展速度十分迅速;在注浆终压较大时,水泥浆液扩散半径扩展速度较缓慢,注浆终压对浆液扩散半径影响的减弱。
2)考虑稠度空间分布不均匀性时,扩散半径随注浆终压上升速度明显比不考虑时的上升速度快。其原因在于,考虑水泥浆液稠度空间不均匀性将会致使浆液黏滞阻力的计算值比实际值高,在注浆终压保持相等时,水泥浆液扩散半径较实际扩散半径偏小,进一步说明了盾构隧道壁后注浆考虑浆液稠度空间分布不均匀性的必要性。
3)注浆终压对浆液扩散半径的影响均表现出随水灰比增大而增大。当浆液扩散半径相同时,水灰比越大,其所需的注浆终压越小。
4.4 注浆终压对管片总压力的影响
实际工程中注浆终压多在1 MPa之内,为了便于研究管片总压力与注浆终压关系,本文设置终压为2 MPa,将相关参数代入式(27)和(31),可得管片总压力随注浆压力变化曲线,如图9所示。
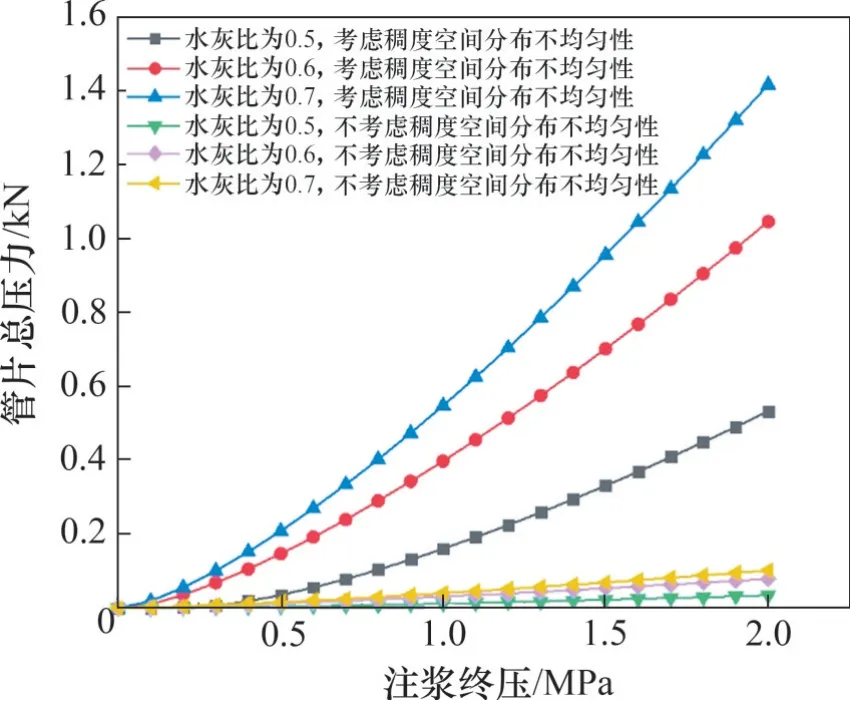
图9 管片总压力与终压变化关系Fig.9 Relationship between total segment pressure and final pressure
由图9可知:
1)采用不同水灰比浆液进行注浆,管片所受总压力均随注浆终压增加而增加,但增幅表现并不一致,其增幅随着水灰比增大而增大。
2)当终压为2 MPa 时,考虑稠度空间分布不均匀时,注浆浆液水灰比为0.7的管片总压力是注浆浆液水灰比为0.5 管片总压力的2.7 倍。不考虑稠度空间分布不均匀性时,注浆浆液水灰比为0.7的管片总压力是注浆浆液水灰比为0.5管片总压力的3.0 倍。基于此,从管片结构的受力安全考虑,不可单纯改变浆液水灰比来提升注浆效果。
3)当注浆终压较低时,考虑与不考虑浆液稠度空间分布不均匀性注浆压力差异较小,但随着注浆终压增大,在2.0 MPa 时两者相差可达13 倍以上。
4)注浆压力从0.2 MPa 到2.0 MPa,水泥浆液扩散半径增大不到2倍,而浆液注浆压力对管片的总和却增加20 倍以上。由此可知,仅仅依靠增大注浆压力来提升浆液扩散半径,将会致使隧道管片因承受浆液总压力过大造成破坏,即单纯通过增大注浆压力来改善注浆效果不可行。
4.5 浆液压强分布
以2.0 MPa为注浆终压,并以此为注浆结束标准,由式(26)和式(29)可得考虑与不考虑稠度空间分布不均匀性的扩散半径,如表2所示。
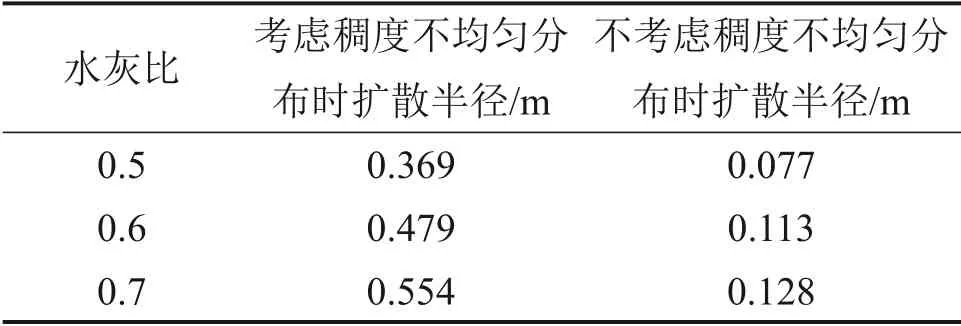
表2 注浆终压2.0 MPa水泥浆液扩散半径Table 2 Diffusion radius of cement slurry with final grouting pressure of 2.0 MPa
将表2中扩散半径与其他相关参数代入式(25)和(30),可得浆液各质点压强随注浆孔中心位置距离变化曲线,如图10和图11所示。
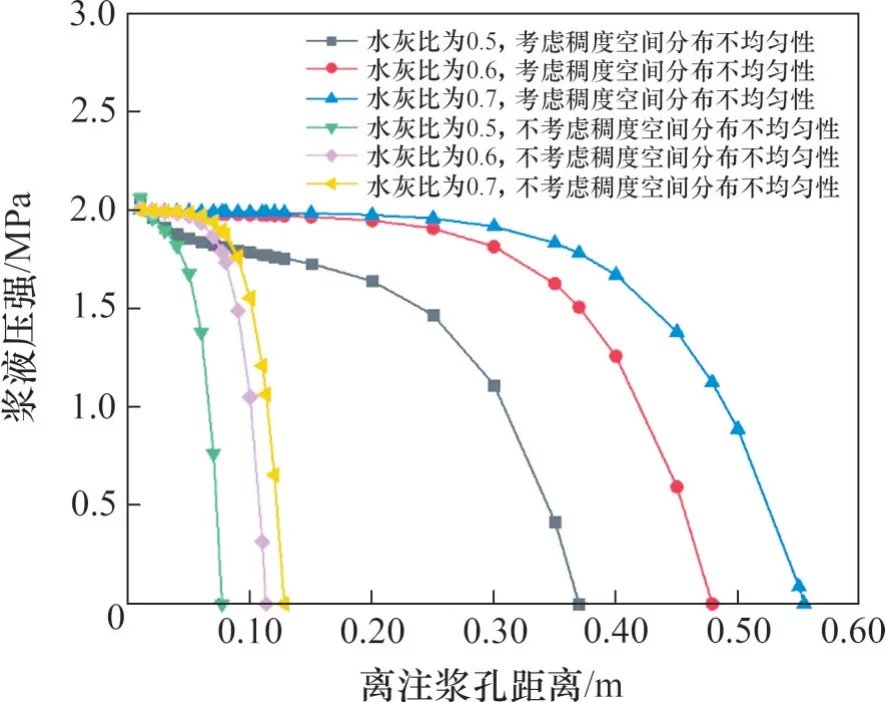
图10 注浆孔距离与浆液压强空间分布关系曲线Fig.10 Relationship curve between the distance of grouting hole and the spatial distribution of slurry pressure
由图10和图11可知:
1)在注浆终压相同的情况下,浆液质点与注浆孔相距越远,其承受压力越小,浆液质点承受压力与扩散距离呈现下抛物线趋势。具体为,在距注浆孔较近时,浆液压强随扩散半径增加而减小,其减小速度较缓慢。在距注浆孔较远时,浆液内部压强随扩散半径增加而迅速下滑,在浆液最大扩散半径处浆液承受压强与外部水压相等。
2)扩散半径相等的不同水灰比浆液承受的压强随浆液水灰比增大而增大。在扩散半径较近处,水灰比对浆液压强影响较小,反之,对浆液压强影响明显。
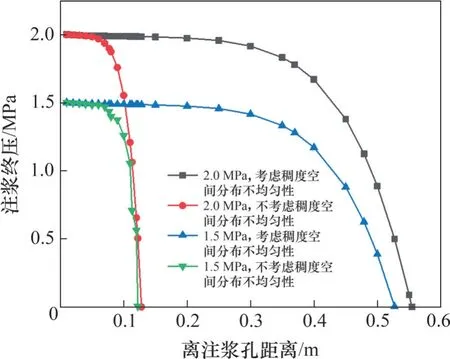
图11 水灰比为0.7浆液压强空间分布关系曲线Fig.11 Spatial distribution relationship curve of slurry hydraulic pressure with water-cement ratio of 0.7
3)不考虑稠度空间分布不均匀性时,随离注浆距离增加,浆液压强下降速度较考虑时更大。
4)在离注浆孔附近,在不同注浆终压下,浆液压强相差较小;随着扩散距离增大,不同注浆终压浆液压强差增大。不考虑稠度空间分布不均匀性时,注浆终压对浆液质点承受压强变化影响较小。
5 结论
1)水泥在水灰比为0.5~0.7 时,浆液符合幂律流体特征,建立了恒定注浆速率条件下考虑稠度时空变化的隧道壁后注浆半球面扩散模型,推导了隧道壁后承受压力的时空分布方程及管片受力计算公式。
2)考虑黏度空间不均匀性时,浆液离注浆孔距离越远,稠度越大,且稠度随距离增加,其增加速率迅速增加,浆液稠度时间函数与浆液稠度空间分布的趋势保持一致;在注浆终压相同时,浆液压强随注浆孔距离增加而减小,在距注浆孔较近的范围内浆液压强减小缓慢,离注浆孔较远距离的浆液压力迅速靠近,接近临界水压力。
3)在注浆终压较小时,随注浆终压增大,水泥浆液扩散半径的扩展速度增加迅速;当注浆终压较大时,水泥浆扩散半径的扩散速度扩展较缓慢;管片承受的总压力均随注浆终压增加而增加显著,其增幅随着水灰比增大而增大;当扩散距离相同时,浆液压强随注浆终压增大而增大。
4)不考虑浆液空间分布不均匀性所得注浆压力是正常值的60 倍以上,所得浆液扩散半径大约是正常值的1/3,管片承受总压力相差20倍以上。
