非饱和土渗透系数试验与模型预测及验证

2021-04-16刘小文罗海林陈嘉帅

南昌大学学报（工科版） 2021年1期

刘小文，罗海林，陈嘉帅

(南昌大学建筑工程学院，江西南昌 330031)

自然界中地表土体绝大多数处于非饱和状态，土体中包含着固、液、气三相，渗流可认为是液相在土体中动态迁移的过程，且不同于饱和土体，在多相的相互影响下，非饱和土的渗流过程十分复杂。对非饱和土渗流运动的分析通常以渗透系数作为基本参数，但非饱和渗透系数受到饱和度、孔隙率、基质吸力、土体结构等因素的影响，直接对非饱和渗透系数的测量颇为不易。为了较为便捷地获取土体的渗透系数，国内外许多学者进行了渗透系数获取方法的研究。直接试验法中，Gardner[1]首先基于压力板仪试验提出的多步溢出法，虽可同时测量渗透系数和土-水特征曲线，但是当试验时间比较长时会产生气泡并集聚在陶土板上，影响测量精度。一维土柱的湿润锋前进法[2]能够在较短时间内直接测量非饱和土的渗透系数，但该方法对土体会有一定的限制[3]。王铁行等[4]利用水平土柱入渗法，通过试验与数据处理，得到了不同干密度黄土-水分扩散率与体积含水量的关系。姚志华等[5]设计一种能够获取黄土原状试样的设备，并与室内重塑试样一起进行了水平土柱试验，对非饱和Q3黄土的渗透特性开展了相关研究，但水平土柱并不能较为真实地反映天然状态下的入渗情况。

除使用直接的试验方法获取渗透系数外，通过使用常用的土-水特征曲线(也即SWCC)和渗透系数模型也可以大致得出土体的渗透系数。Genuchten[6]提出的VG模型得到了广泛的应用。后来通过利用VG模型拟合的SWCC曲线的参数代入Mualem模型方程[7]中得出了非饱和土渗透系数。Fredlund等[8]发现，土-水特征曲线方程的参数相互不独立，无法独立分析每个参数对渗透系数的影响。Childs等[9]提出的Childs & Collis-George(CCG模型)也得到了广泛的运用；Fredlund等[10]在Childs & Collis-George孔隙分布模型的基础上，推导出了一个建立在整个土-水特征曲线上的渗透系数函数。Rahimi等[11]研究发现，在高吸力范围内，渗透系数的预测效果相对较差。为此国内外学者也作出了一定的改进，Rahimi等[12]将现有的SWCC方程和可用的相对渗透率KR方程相结合，研究了SWCC方程和相对渗透率KR方程在非饱和渗透率函数估计中的作用。蔡国庆等[13]提出了一种可以基于SWCC试验量化初始孔隙比的方法，以此开展了初始孔隙比对非饱和土相对渗透系数影响的研究。孙大松等[14]建立了基于土体孔隙分布的分形模型，推导出采用分维数与进气值表示的渗透系数的理论表达式。

由于现存的各种方法都存在一定的缺陷，数值模型常为经验公式且没考虑干湿循环的影响[15]，加上试验又耗时较长、操作较为复杂且不能得到准确的渗透系数，在工程运用中也不清楚哪种方法最为适用。就江西红土而言，其分布面积广泛，大量运用于工程建设中，所以对红土的渗透系数的研究尤为重要，但是目前在该领域的研究较少。本文通过压力板仪试验和一维垂直土柱渗流试验，并结合CCG模型和VGM模型对土体的非饱和渗透系数进行研究，利用Geo-Studio数值模拟对试验及模型结果进行对比验证。结果表明；动态多步溢出法与CCG模型预测的结果更为吻合，且略小于渗流实际情况。湿润锋前进法能够较好地适用于江西地区红土，由于土柱试样较大减少了边界影响，结果与实际情况更为接近，为指导工程实践提供一定参考。

1 基本原理

1.1 动态多步溢出法渗透系数计算

溢出法作为一种瞬态试验方法，最早于1956年由Gardner[1]基于压力板仪试验提出。利用压力板仪进行动态多步溢出法的试验不仅可以测得非饱和土的土-水特征曲线，也可测得非饱和土在不同基质吸力下的渗透系数[16-19]，公式如下：

(1)

(2)

1.2 Childs & Collis-George模型预测渗透系数

采用Childs等[9]提出的Childs & Collis-George模型后经过Marshall等[20]改进和Kunze等[21]的修正后，完善成为一种以任意孔径分布为基础预测非饱和渗透系数的模型，通过模型预测江西红土的非饱和渗透系数。其渗透系数表达式如下：

(3)

(4)

式中：ks为实测饱和渗透系数；ksc为计算的饱和渗透系数；Ad为调整系数；Ts为水的表面张力；ρw为水的密度；g为重力加速度；μw为水的绝对黏度；θs为饱和体积含水率；kw(θw)i为对应于第i等分中点的体积含水率(θw)i的渗透系数；p为计及不同尺寸孔隙的相互作用的常数，可假设其为2.0；m为试验土-水特征曲线上饱和体积含水率与最小体积含水率之间的等分数；N为饱和体积含水率与零体积含水率之间的计算间断总数，N=m[θs/(θs-θL)]，θL为相应于试验土-水特征曲线上的最小体积含水率，m≤N；(ua-uw)j为相应于第j个间段中点的基质吸力值。

1.3 Van Genuchten-Mualem模型预测渗透系数

将VG模型[6]代入Mualem模型[7]获得Van Genuchten-Mualem模型，其表达式为

(5)

(6)

式中：Se为有效饱和度；θ为体积含水率；θs为饱和时体积含水率；ψ为基质吸力；θr为残余体积含水率；ks为饱和渗透系数；a、n、m为拟合参数，通常有m=1-1/n。

由于残余含水率θr的确定颇为困难，由汪东林等[22]将残余含水率θr假定为0进行的数据拟合结果发现影响较小，故本文VG模型拟合采取θr=0。

1.4 湿润锋前进法计算渗透系数

图1为水在土柱中的湿润锋运动示意图。A为垂直土柱的底端断面，B为土柱的监测断面，降雨历时分别为t1和t2时湿润锋分别发展到断面M1和M2。

图1 湿润锋移动示意图Fig.1 Schematic diagram of wetting peak movement

通过计算湿润锋传导率便可以得出非饱和土的渗透系数：

(7)

式中：θ(h,t)为垂直土柱体积含水率分布函数；ψ(h,t)为基质吸力分布函数；θ0为垂直土柱的初始体积含水率；γw为水的重度；v为湿润锋前进的平均速率。v取湿润锋前进的平均速率，利用监测点的体积含水率与基质吸力关系，试验数据经过VG模型拟合后可以用于计算，将数据代入式(7)可以对非饱和渗透系数进行计算。

2 试验设计

对比采用GEO-Experts压力板仪试验和一维垂直土柱渗流试验，对渗流情况及渗透系数的确定展开研究。

2.1 垂直一维土柱试验装置

自行设计定制的有机玻璃圆柱桶(图2所示)，高度为100 cm，外径为50 cm，内径为48 cm。采用MPS-6土壤水势传感器测量基质吸力，水势传感器由一个湿度传感器与一块已知水分释放曲线的多孔材料组成，当多孔材料与周围土壤达到水分平衡后，湿度传感器测量多孔材料的水分含量，并根据水分释放曲线将水分含量换算成水势。而且MPS-6使用一种特制陶质材料，具有非常大的孔径范围，这使得MPS-6适合测量的水势范围很大。土壤水势传感器的数据记录使用手持式ProCheck多功能读表，见图3。采用MS10土壤水分传感器测量土体的含水率，运用自动化数据采集箱对水分传感器的数据进行采集，见图4。圆柱筒用来装载土样及预先放置土壤水分传感器和水势传感器，沿着有机玻璃柱两侧对应高度位置打有两种不同尺寸的预留孔洞，一侧预留孔用来安装MS10土壤水分传感器，另外一侧安装MPS-6水势传感器，传感器的安装位置见图5。

图2 空心有机玻璃圆柱Fig.2 Hollow plexiglass cylinder

图3 水势传感器多功能读表Fig.3 Water potential sensor and multifunctional reading table

图4 含水率数据自动化采集箱Fig.4 Automatic collection box for moisture content data

图5 传感器安装位置示意图(单位：cm)Fig.5 Schematic diagram of sensor installation location

2.2 试验步骤

1) 试验开始前，配制初始含水率的湿土，加水喷洒后搅拌均匀，用膜布盖上静置24 h，静置后复测含水率。

2) 计算10 cm高土柱所需湿土质量；称取所压到10 cm高度处所需湿土放入有机玻璃桶内，用自制压实器均匀压实；重复此操作，直至土柱装填到70 cm高，层与层之间刮毛处理，确保连接紧密，不出现断层。在土柱分层压实的过程中向有机玻璃侧壁涂抹少量凡士林来有效减小边界效应的影响。

3) 土柱填筑至预埋传感器位置时，在有机玻璃筒的侧壁垂直插入传感器探头，此做法是避免土柱填筑完成后再插入水分传感器会对土样造成扰动，传感器与有机玻璃柱壁之间用热熔胶密封，以防止试验过程中水分和气体的泄露。

4) 在土柱顶部均匀铺设5 cm厚细砂，尽量保证水分下渗均匀，防止在渗水过程中试样表层板结或沿侧壁集中下渗；用喷水壶持续、缓慢、均匀加水，加水结束后，立即将顶部盖上，盖子与有机玻璃柱连接处涂抹凡士林，将其与有机玻璃柱连接起来形成密闭空间，防止水分散失。

5) 通过水分传感器与水势传感器记录体积含水率变化以及对应的基质吸力值，做好记录。

2.3 试验方案

试验用红土土料取自南昌市某公路路基筑基用土。土料完全干燥状态色泽呈红褐色，按照土工试验标准(GB/T 50123—1999)对试验备用土料进行了：1) 筛分试验；2) 比重瓶试验；3) 轻型击实试验；4) 液塑限测定试验。得到了土样的基本物理力学性质指标参数见表1所示。

表1 试验用红土基本物理指标参数Tab.1 Basic physical parameters of laterite used in the test

土体含水率越低，其渗透系数越小，土体内的渗流运动越慢，为获取较大饱和度范围的数据，同时也为了避免由于土体初始含水率过小导致前期渗流等待时间过长，设置土柱的初始体积含水率为10%。利用喷壶缓慢地在上层加水，一共加水10 L。利用预先埋置在不同深度的传感器采集数据，记录不同深度体积含水率、基质吸力与时间的变化关系，土柱试验方案见表2。

表2 一维垂直土柱试验方案Tab.2 One-dimensional vertical soil column test plan

3 试验结果

3.1 动态多步溢出法土-水特征曲线试验结果

将制备好的不同压实度的土样置于GEO-Experts压力板仪，逐级增加气压后无需等待试样的内部气压力平衡后再进行加压，试验首先通过气压控制系统施加至第1级气压5 kPa，气压持续不变直至t1时刻(试样在此时尚未到达平衡状态)；随后按照气压施加顺序将气压增加至第2级气压25 kPa，并且保持该气压不变直至t2时刻；以此类推，增加气压至第7级气压400 kPa，直至tn时刻。做好未达到平衡状态试样在每级气压下溢出水量和时间的记录，通过溢出水量反算处于不同时间与不同基质吸力的含水率，动态多步溢出法在不同压实度下的试验数据如图(6)所示。

饱和度图6 不同压实度下试验结果Fig.6 Test results under different compaction degrees

3.2 动态多步溢出法渗透系数试验结果

根据试验中试样的初始状态参数：初始饱和度、初始吸力值和饱和试样中水的质量，得到每级压力下、各个时刻试样的饱和度。此通过试验得到了饱和度随时间的演化方程，采用最小二乘法，求解出每级压力下相对应的C和值。根据求得C和值代入式(1)和式(2)，通过编制程序计算，可以求得渗透系数kw的计算结果见图7所示。

饱和度图7 试样渗透系数与饱和度关系Fig.7 Relationship between permeability coefficient and saturation of sample

3.3 CCG和VGM模型渗透系数拟合结果

CCG模型利用3.1节中土-水特征曲线的结果代入式(3)和式(4)计算结果见图8所示；VGM模型利用3.1节中土-水特征曲线的结果代入式(5)和式(6)计算结果见图8所示。

饱和度图8 不同压实度下饱和度与渗透系数关系Fig.8 Relationship between saturation and permeability coefficient under different compaction degrees

3.4 湿润锋前进法试验结果

3.4.1 湿润锋前进平均速率

采用湿润锋前进法进行数据处理，当传感器数值达到峰值后持续一段时间内不再明显增加即代表湿润锋已运移于此。对各试样湿润锋抵达不同深度监测点的数据进行整理，见图9。刚开始加水时由于土的渗透性较小，在土柱上部会有积水，土柱内土体在上部会先出现一段饱和区。在入渗的初始阶段速率会较快，到一定时间后速率趋于稳定。反映在湿润锋抵达各监测点时间上，入渗深度超过15～25 cm后湿润锋移动的速率较之前有所下降，也可以看到压实度越高的试样这种下降越不明显。对数据进行计算，可以得到不同压实度的土柱试样其相邻监测点每一段土柱内湿润锋前进的平均速率，计算结果见表3。

t/min图9 湿润锋抵达各监测点的时间Fig.9 Time when the wet front reaches each monitoring point

3.4.2 土柱中含水率与基质吸力的确定

通过预埋在同一深度的土壤水分传感器和土壤水势传感器，可以确定含水率与基质吸力的关系。图10为各压实度土柱试验的含水率与基质吸力关系图，可以看到深度分别在15、35 cm处测量得到的含水率与基质吸力曲线非常接近，误差很小，表明制作的土柱均质性很好，所以各压实度试样其余深度监测点的基质吸力与含水率关系也符合其关系曲线。刘星志[23]也提出Van Genuchten模型最为适合，故对试验数据采取VG模型进行了土-水特征曲线拟合，a、b、m为拟合参数，R2为相关系数的平方，拟合参数结果见表4。

表3 湿润锋前进平均速率Tab.3 Average forward velocity of the wet front

基质吸力/kPa(a) 压实度85%

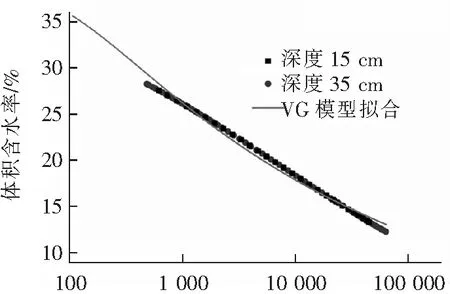
基质吸力/kPa(b) 压实度90%

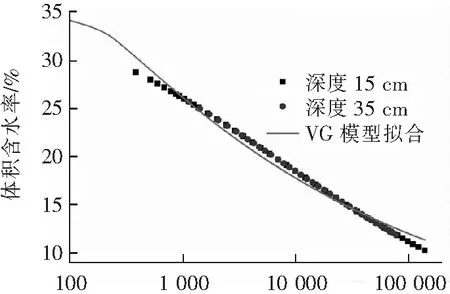
基质吸力/kPa(c) 压实度93%

基质吸力/kPa(d) 压实度95%图10 各压实度土柱试验的土-水特征曲线试验数据与拟合Fig.10 Test data and fitting of soil-water characteristic curve of soil column test with various compaction degrees

表4 土柱试验VG方程拟合参数表Tab.4 Fitting parameter table of VG equation in soil column test

3.5 计算结果

利用式(7)，结合表2、表3和表4中参数求解得到不同压实度下渗透系数与饱和度关系，如图11所示，同一试样内不同深度的渗透系数也存在着差异性，非饱和土渗透系数随着深度发生变化。同一试样，随着深度的增加，非饱和土渗透系数逐渐减小。其原因在于一次性加水，加水后引起上部含水率的迅速增加，对于计算存在一些扰动影响。随着入渗的持续，土柱中其余深度湿润锋过境含水率稳定增长，计算结果趋于稳定。而对于监测点5，由于埋深深度较深，加水后水分运动距离过长，计算渗透系数偏小。

饱和度(a) 压实度85%

饱和度(b) 压实度90%

饱和度(c) 压实度93%

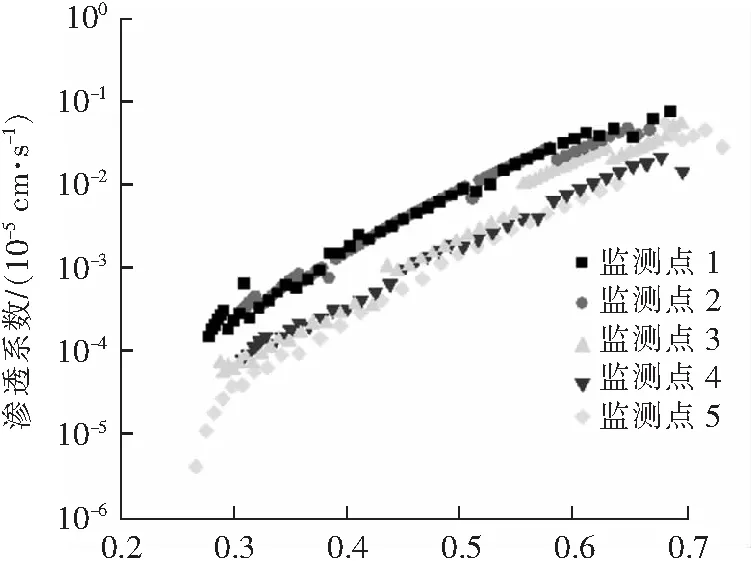
饱和度(d) 压实度95%图11 一维土柱法各压实度的渗透系数关系

3.6 结果拟合

由图11可以看到，监测点3、4的数据由于埋置深度较深，受加水后含水率快速增大的影响较小，两个监测点计算得到的渗透系数非常接近且相对符合实际。故取监测点3、4的渗透系数作为数据点对渗透系数与饱和度函数关系进行拟合。

通过研究发现，非饱和渗透系数的对数lgk与饱和度Sr呈现线性关系，拟合关系为：

lgk=a+bSr

(16)

其中：k为渗透系数，cm·s-1；Sr为饱和度，范围为0～1。表5为各压实度下渗透系数与饱和度关系的拟合参数，图12为各压实渗透系数拟合直线图。由图12可以看出，压实度的影响下非饱和渗透系数的对数lgk与饱和度Sr仍呈现线性关系。

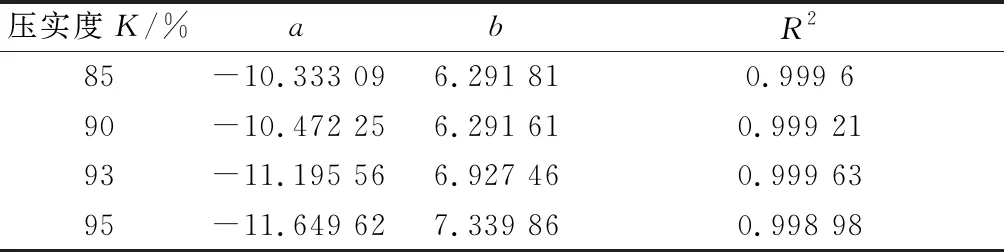
表5 非饱和渗透系数与饱和度拟合参数Tab.5 Unsaturated permeability coefficient and saturation fitting parameters

饱和度图12 一维土柱法渗透试验拟合直线Fig.12 Fitting straight line for one-dimensional soil column permeability test

4 4种方法下渗透系数与饱和度关系曲线对比

将基于动态多步溢出法、土-水特征曲线预测得到的渗透系数，与土柱法试验得到的渗透系数进行比较分析，见图13。

饱和度(a) 压实度85%

饱和度(b) 压实度90%

饱和度(c) 压实度93%

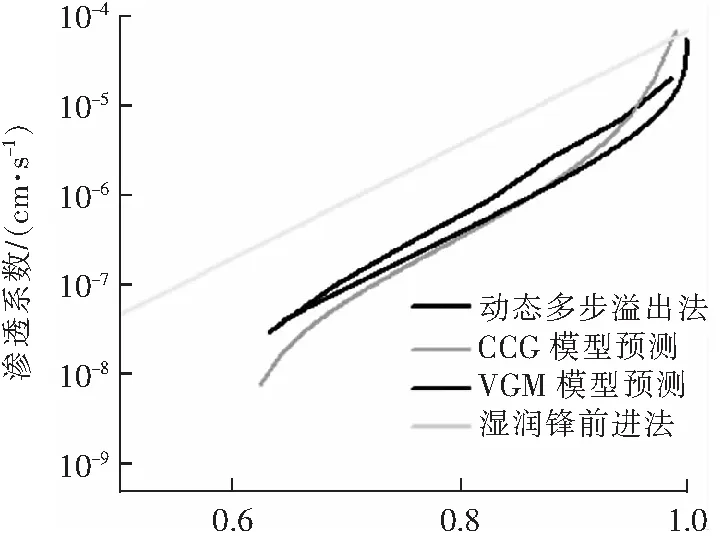
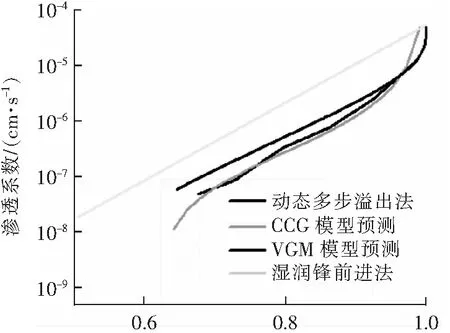
饱和度(d) 压实度95%图13 各方法求解的渗透系数函数对比Fig.13 Comparison of permeability coefficient functions solved by various methods

对比发现:4种模型计算的渗透系数都是随着饱和度的下降而减小，其渗透系数随饱和度的变化规律一致；采用湿润锋前进法计算得到的渗透系数比另外3种方法的要更大一些，相差5～10倍。其中，VGM模型除了压实度为90%试样外，其余3种压实度下预测的渗透系数与湿润锋前进法相差5倍以内。

经过两种模型预测的渗透系数与基于动态多步溢出法求解的渗透系数函数都非常接近，CCG模型对于基于多步溢出法计算的渗透系数有更好的相似性，在饱和度0.6～1.0范围内，渗透系数几乎重合。两种预测模型中，CCG模型预测动态多步溢出法计算的渗透系数效果最好。

湿润锋前进法与动态多步溢出法计算的渗透系数随饱和度变化的趋势一致，但在相同的饱和度下，湿润锋前进法的计算结果比动态多步溢出法要大10倍左右，原因可能是湿润锋前进法是使用土柱试验计算，土柱试样比溢出法的试样大得多。

5 土柱渗流试验的数值模拟

5.1 模型建立与参数设置

通过在Geo-Studio软件内的seep/w模块里构造相同大小的数值模型，设定与试验条件相同的入渗边界来进行数值模拟试验，可以再现试验室一维垂直土柱的渗透试验过程。同时将计算得到的4种非饱和渗透系数函数关系代入数值模拟中，对数值模拟结果与实际试验结果进行数据研究，验证多种方法计算得到的渗透系数的正确性，并找出最符合实际渗流的渗透系数。

土柱体模型在二维上呈现的尺寸为高0.7 m，宽度0.48 m，网格间距X与Y方向均为0.01 m。模型顶部加水为入渗边界，左右边界均为不透水边界，底部为透水边界与大气连通。计算模型如图14。

土柱全部由红土填充，入渗水头边界设置为单位流量随时间变化的函数。对模拟入渗采用瞬态渗流分析，在瞬态渗流分析中需要对土体的渗透性函数和土-水特征曲线进行定义。采用VG模型拟合的土-水特征曲线及3种不同方法计算得到的4种渗透系数函数，将饱和体积含水率代入seep/w中设置体积含水率函数与渗透系数函数。

因为材料的初始含水率对渗流分析有影响，且要与土柱试验保持一致，需要在土体材料参数内激活初始孔隙水压力。土柱试验土样的初始体积含水率θ=10%，在拟合土-水特征曲线中取对应的初始孔隙水压力数值对材料赋值；然后，选择之前确定的土-水特征曲线和非饱和渗透系数函数，数值模拟持续时间与土柱试验保持一致，取2 600 min。

监测面的设置与2.3.2节土柱试验中一致，选择深度分别为5、15、25、35、45 cm作为监测面，计算完成后可以直接获取土体内任意一监测面有关参数随时间变化的数据，监测面示意图如图14所示。

图14 数值模型Fig.14 Numerical model

5.2 不同压实度下湿润锋的时程曲线拟合结果对比

图15为湿润锋抵达各监测点的时程曲线图，可以清楚地看到，4种不同渗透系数函数对于模拟还原湿润锋的运动过程其规律相似。其中，采用湿润锋前进法求得的渗透系数函数的模拟工况，在4种压实度工况中都与实际试验的数据很好地贴合，只是湿润锋抵达监测点的时间有一些提前，可以理解为其湿润锋前进法计算的渗透系数要稍大于实际渗流情况。而基于土-水特征曲线采用两种模型预测以及基于动态多步溢出法计算得到的渗透系数函数，其湿润锋运动时程曲线的模拟结果比实际试验有一些延后。