考虑Pareto改进的售电公司最优购售电模型

2021-04-16黄煌杨胡萍彭鑫周睿肖思敏

南昌大学学报（工科版） 2021年1期

黄煌，杨胡萍，彭鑫，周睿，肖思敏

(南昌大学信息工程学院，江西南昌 330031)

2015年“中发9号文”特别指出新一轮电改应当开放售电业务，培养售电侧各竞争主体，为发电厂和用户提供更多直接交易通道和交易选择机会，在文件指导下国内大量售电公司相继成立[1]。随着近年来交易模式规范化，售电市场份额日趋饱和，诸多省份出现售电公司相继退市的情况，对售电公司购售电策略进行研究，有助于售电公司走出困境，转亏为盈[2]。

售电公司购售电策略分析，目前研究主要针对售电定价方法和调度优化方法，其中售电定价方法的核心主要在于使用电价理论，通过多市场组合购电、制定用户购电套餐达到增加售电利润的目的[3-4]。调度优化方法主要分析售电公司通过自身或者其他主体持有储能装置、光伏发电装置等设备对各时段购售电量进行调度，达到售电公司效益最大化[5-6]。文献[7]充分发挥用户可中断负荷对售电量曲线的调整能力，鼓励售电公司采用和用户签订需求响应合同的方式规避尖峰电价带来的风险；文献[8]对电能氢气转换技术进行了说明，提出售电公司可以通过加装氢储设备来提高售电调节能力，同时利用氢储设备参与辅助服务市场创造收益；文献[9]提出售电公司制定售电策略时应考虑园区内可控式负荷、可控分布式电源、储能设备、风力发电和光伏发电对用户需求电量的影响，并以社会成本最小为目标建立了园区售电商出清和运行优化模型；文献[10]基于大数据使用LSTM-SVM算法将电力用户分为3类，并根据这3类用户用电特性及其负荷预测结果为售电公司制定针对性电能调度策略提供指导。以上调度优化方法的研究可以提升售电公司售电能力，但是没有考虑其他市场参与主体持有有限生产资料，盲目增加售电量会损害其他主体利益的情况。

Pareto改进作为福利经济学的重要工具，具有保障市场参与成员福利的功能，常被运用于解决多选择背包问题。文献[11]提出利用Pareto相关理论解决有轨电车储能电池和超级电容的容量配置多目标优化问题，在满足体积、质量约束的情况下，降低了单位输出功率下的电能损耗。文献[12]提出将Pareto改进运用在电力市场领域，建立一种兼顾效率与帕累托改进的电力市场竞价模式，避免售电公司因追逐利润最大化对其他市场主体利益造成损害，有助于电力市场稳定。

本文针对电力市场各主体交易行为，考虑售电公司购售电对其他主体造成影响，基于罚函数法加入Pareto改进约束，使用QPSO算法以加入Pareto改进约束罚函数后的售电公司利润函数最大化为目标，建立售电公司购售电模型。通过与传统不考虑Pareto改进的售电公司购售电模型进行对比，验证了本模型在提高市场总利润，在策略更新过程中保障各个主体利润、避免系统在约束边界运行、降低系统风险的有效性。

1 市场主体利润建模

电力市场中主体主要有发电公司、售电公司、电网公司和电力用户，本文针对这4类主要参与主体进行分析。

1.1 售电公司利润建模

假设售电公司从现货市场购买电能，并以固定价格对用户出售，输电费用和输电过程中产生的线路损耗均由售电公司承担。根据上述假设，售电公司在第t小时获得利润应为：

RR,t=PR2UQR2U,t-(PG2R,t+PP2R)QG2R,t

(1)

QR2U,t=QG2R,t-Qloss,t

(2)

Qloss,t=(1-η)QG2R,t

(3)

式中：PR2U为售电公司向电力用户出售电量的售价；QR2U,t为售电公司在第t小时向电力用户出售的电量；PG2R,t为发电公司与售电公司在第t小时的结算价格；PP2R为电网公司提供输电服务收取的输电价格；QG2R,t为发电公司在第t小时向售电公司出售的电量；Qloss,t为第t小时电能运输过程中造成的线路损失电量，其与输电导线型号、输电线路电压等级、负荷功率因数密切相关，可以用效率η进行表示，通常输电线路综合效率为95%～97%。

售电公司购买电量需要满足线路传输功率约束：

0≤QG2R,t≤QLinemax

(4)

式中：QLinemax为输电线路最大传输容量。

1.2 其他公司利润建模

假设发电公司使用火力发电机组，其发电成本可使用二次函数进行表示，则发电公司在该交易行为中获得利润可表示为：

RG,t=PG2R,tQG2R,t-CG2R,t

(5)

(6)

式中：CG2R,t为发电公司在第t小时向售电公司出售电能带来的发电成本；c1、c2、c0分别为火电机组发电成本的一次系数、二次系数和常系数，该值可以通过统计手段利用数据拟合方法得到。

发电公司出售电量应满足火电机组爬坡约束和最大最小出力约束：

QG2R,t-QG2R,t-1≤KGmax

(7)

QGmin≤QG2R,t≤QGmax

(8)

式中：KGmax为火电机组最大爬坡功率；QGmax和QGmin为火电机组最大出力功率和最小出力功率。

假设在电力市场改革环境下，电网公司作为管道型企业，通过收取输电费用进行盈利，则电网公司在交易中获得利润为：

RP,t=PP2RQG2R,t-r

(9)

(10)

式中：r为不同负荷水平下电网公司承担的风险，其与线路负荷水平呈线性正相关,当负荷水平超出安全裕度后，风险将随负荷增长而增加；k为EENS的价格比例系数；S为电量不足期望(expected energy not supplied,EENS)；k′为等效后的比例系数；QLineN为线路经济输送容量；β为输电线路安全裕度[13-14]。

假设电力用户为持有有限生产资料的工业园区，参考文献[15]工业用户效用函数构建利润模型，模型如式(11)、式(12)所示。

RU,t=UU,t-PR2UQR2U,t

(11)

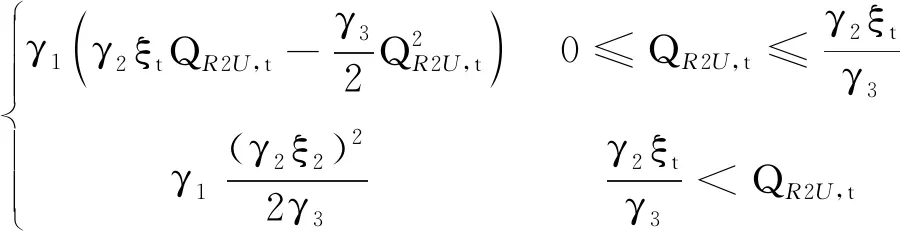
(12)

式中：UU,t为电力用户在第t小时内的效用值；γ1、γ2和γ3分别为效用函数的特征参数，可以对工业园区内工业用户效用进行调查统计得到；ξt为与时间相关的随机数，代表了随机扰动量对用户效用的影响，由于电力用户所持有的生产资料是有限的，因此当电量使用达到一定程度，用户生产能力趋于饱和，效用将不再增加。

2 Pareto改进约束下的QPSO寻优

2.1 Pareto改进约束

售电公司购售电决策的制定不但会影响自己的利润，还会影响市场内其他主体的利润，以降低其他主体利润来提升自身利润的售电决策，必然会被市场中利润受损的主体所抵制。为了促进市场繁荣，实现多主体共赢，提高售电策略的接受程度，在不损害其他主体利润的条件下实现售电公司利润最大化，使用罚函数法建立Pareto改进约束，以售电公司利润最大化为目标，考虑该约束对购售电策略进行寻优。

Pareto改进是指在没有任何主体境况变坏的前提下，通过一种决策使得至少一个主体境况变得更好。Pareto改进的数学模型表示为：

Ri=fi(X1,X2,…,Xd)

(13)

(14)

(15)

(16)

以售电公司日利润最大化为目标，加入Pareto改进约束罚函数对其进行寻优。约束罚函数和目标函数F可以表示为：

(17)

p′=ω(bother+bpareto,R+bpareto,G+bpareto,P+bpareto,U)

(18)

(19)

式中：bother为综合了线路传输约束、火电机组爬坡约束和出力约束的偏差；bpareto,R、bpareto,G、bpareto,P、bpareto,U分别为售电公司、发电公司、电网公司和电力用户Pareto改进约束的偏差，偏差越大，所得解越不满足约束条件；ω为惩罚因子；p′为不满足约束所导致的综合惩罚量。

使用量子粒子群算法(QPSO)对售电公司购售电策略更新过程进行模拟，将每次迭代后所得全局最优解作为售电公司新的策略，实现策略的寻优。

2.2 QPSO寻优

QPSO结合量子力学相关理论，借助势阱模型和波函数构建粒子寻优模型，利用蒙特卡洛随机模型反演粒子新的位置，克服了传统PSO算法移动方向固定、寻优范围不断缩小、寻优路径无法布满整个解空间的缺陷，是一种适合运用于工程计算、策略寻优的高可靠性智能算法[16]。

QPSO中第j个粒子的吸引子e位置和粒子位置更新公式为：

ej(l)=φj(l)Ej(l)+[1-φj(l)]G(l)

(20)

(21)

QG2R,j=(QG2R,j,1QG2R,j,2…QG2R,j,24

(22)

(23)

式中：T为最大迭代次数；l为当前迭代次数；Ej为粒子最优位置；G为全局最优位置；N为粒子总数；α为QPSO收缩扩张系数，随着迭代次数增加，α将从a线性变化为b；μj和φj为服从0～1均匀分布的随机数，可通过蒙特卡洛随机模拟确定[17]。

QPSO计算流程如图1所示。

图1 QPSO计算流程图Fig.1 QPSO calculation flow chart

为方便计算，在求取初始粒子适应度值、生成粒子最优及全局最优步骤时设置Pareto改进惩罚量为0。

3 计算与分析

假设市场内存在火力发电公司、售电公司、电力用户各1个，电力用户类型为大型工业园区，输电服务由电网公司提供，发电公司与售电公司在现货市场的结算价格如图2所示。

t/h图2 现货市场结算电价图Fig.2 Spot market settlement electricity price chart

其他相关参数取值可见表1。

表1 参数取值表Tab.1 Parameter value table

使用QPSO算法在粒子种群大小为10，最大迭代次数为200，QPSO收缩扩张系数中a、b分别取值为1、0.5，惩罚因子为5 000分别以售电公司利润函数最大化为目标和以加入Pareto改进约束罚函数后的售电公司利润函数最大化为目标对售电公司购售电策略进行寻优，4个市场主体在这两种购售电策略下利润如图3、图4所示。

代数图3 不考虑Pareto改进约束下各主体日利润Fig.3 Without considering the daily profit of each subject under the constraint of Pareto improvement

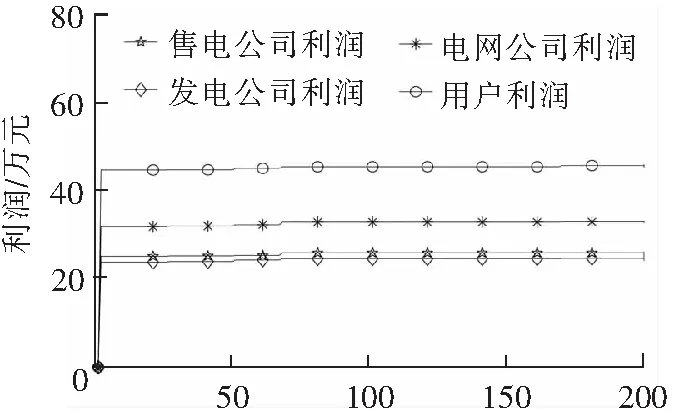
代数图4 考虑Pareto改进约束下各主体日利润Fig.4 Consider the daily profit of each subject under the constraint of Pareto improvement

在不考虑Pareto改进约束的情况下，寻优初期发电公司、电网公司和电力用户日利润随着售电公司日利润增长而增长，直至电力用户日利润达到最大。在50次迭代后，售电公司、发电公司和电网公司日利润继续增加，但是增速明显减缓，电力用户日利润反而下降。最终，售电公司、发电公司、电网公司和电力用户日利润分别为29.6万元、27.9万元、37.8万元和29.1万元，市场总日利润124.4万元。

在考虑了Pareto改进约束的情况下，寻优初期发电公司、售电公司、电网公司和电力用户日利润均快速增加，当增加到一定程度，增加速度急剧减缓。随着迭代次数增加，4个市场主体日利润出现小幅增加，增加时不会导致其他主体日利润减少。最终，售电公司、发电公司、电网公司和电力用户日利润分别为25.9万元、24.6万元、32.9万元和45.6万元，市场总日利润为129万元。

以策略更新带来的利润削减作为指标分析市场参与主体对新策略的抵触情况，利润削减量越大则参与主体对新策略抵触越强烈。

Di,l=|min(0,Ri,200-Ri,l)|

(24)

(25)

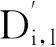
不考虑Pareto改进约束情况下电力用户DU,l,如图5所示。

代数图5 最优策略下电力用户利润削减Fig.5 Users cut profits under the optimal strategy

电力用户利润削减先从0增长至最大值，再随着迭代次数增加逐渐减小，在第14次迭代时有最大利润削减为19.1万元，使用最优策略对该策略进行更新时电力用户抵触最强烈，其他主体利润削减DR,l、DP,l、DG,l始终保持为0，因此不会产生抵触。

考虑Pareto改进约束情况下，使用最优策略对各迭代下采用策略进行更新时各主体利润削减均为0，不会产生抵触。

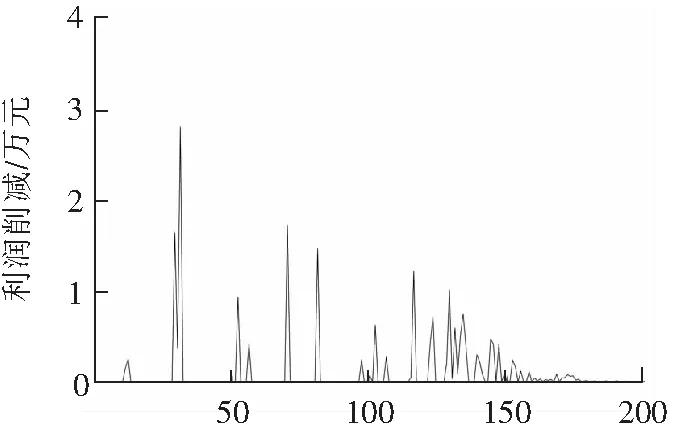
代数图6 新策略下电力用户利润削减Fig.6 Users cut profits under the new strategy

用户利润削减情况断续出现，随着迭代次数增加，利润削减量逐渐减少，全过程最大削减量为2.7万元，相对使用最优策略进行一次更新，采用逐次更新电力用户产生抵触更小。

考虑Pareto改进约束情况下，使用各次当前迭代下采用策略对上一代迭代下采用策略进行更新时各主体利润削减量均为0，不会产生抵触。

两种方法下的售电公司最优购售电策略如图7、图8所示。

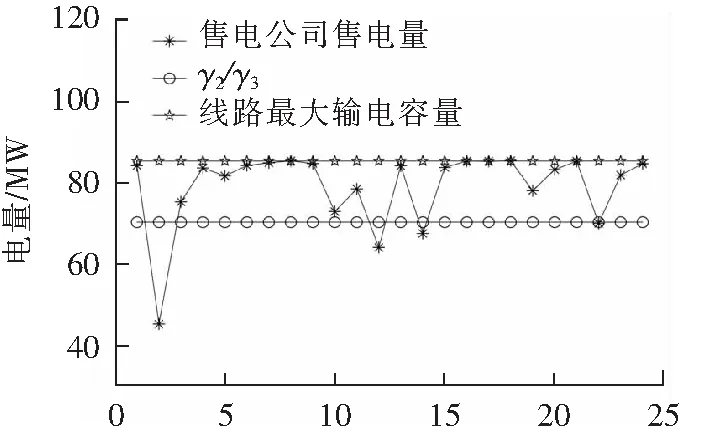
t/h图7 不考虑Pareto改进约束下各时段售电量Fig.7 Without considering Pareto improvement constraint for electricity sales in each period

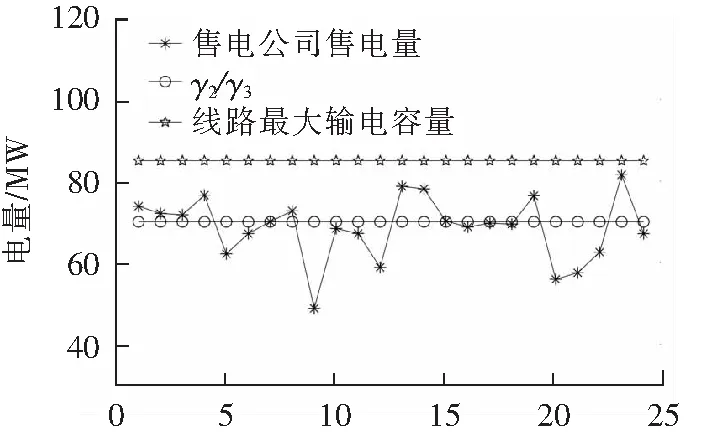
t/h图8 考虑Pareto改进约束下各时段售电量Fig.8 Considering Pareto improvement constraint for electricity sales in each period

若ξt取值为1，电力用户最大生产能力时的用电量为图中γ2/γ3曲线，未考虑Pareto改进约束的情况下，售电公司各小时售电量接近线路最大输电容量，出售电量明显高于电力用户所能使用最大电量，用户购买超出部分电量不但无法获得更多利润，反而增加了其购电成本，这是图3中电力用户利润降低的主要原因。

考虑了Pareto改进约束的售电公司各小时售电量分布在γ2/γ3曲线两侧，距离线路最大输电容量存在一定距离，售电公司售电量曲线与γ2/γ3曲线存在差值是由于ξt波动导致，其与用户投入生产人员数量、机器维护情况、订单量以及其他影响用户最大生产效率的因素有关。加入Pareto改进约束可以促使售电公司在满足电力用户最大效用情况下进行购售电，有效地避免系统在约束边界运行，降低系统运行故障风险。