信息融合算法在空间飞行器自由段跟踪中的应用

丁力全,吴 楠,孟凡坤,王 静

(1.战略支援部队信息工程大学,河南 郑州 450000;2.战略支援部队兴城特勤疗养中心,辽宁 兴城 125100)

信息融合是指将来自多个传感器或多源信息通过协调优化以及综合处理,产生新的有效信息,从而获得更为准确、更可信的结果[1]。目标跟踪领域,融合系统的结构主要包括集中式融合、分布式融合方式[2]。其中,集中式融合可以获得最优融合的估计,但它存在运算量较大，容错性能不强等缺点,如果个别传感器传送错误信息,将导致估计总体性能变差或造成跟踪目标丢失等情况[3]。而分布式融合能够减小融合中心中主滤波器的运算量,并对来自传感器的信息进行有效融合。对于分布式融合系统,早期Singer等提出凸组合融合算法,当每条航迹之间不存在过程噪声且传感器初始时刻估计误差不相关时,凸组合可看作是最优算法[4]。但在实际情况下,这一假设难以得到满足,由于过程噪声的存在和局部传感器之间的误差相关性,Bar-Shalom Y和Campo L提出Bar-Shalom-Campo算法[5],将其应用在工程实际中。随后Carlson 提出联邦滤波器概念,基于信息分配原则,实现了全局最优估计[6]。该算法在计算效率和容错性方面相对上述其他算法有明显的提升。

由于空间飞行器跟踪系统的非线性极强,因此跟踪滤波器的选定应该满足非线性的运动规律。由于UKF滤波相对于EKF无论从运算量还是精度方面,在非线性系统滤波中是较好的滤波方法[7],因此,本文选用UKF滤波算法作为滤波融合的主要算法。

1 空间飞行器自由段动力学模型

本文主要研究通过雷达观测获取飞行器的测量参数,因此在地固系中描述飞行器飞行状态较为合适。当飞行器在自由段运动时,不仅受地球引力影响,还受非惯性附加力,因此自由段目标动力学方程可以精确构建[8]。

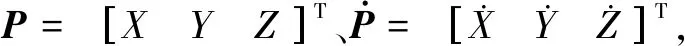
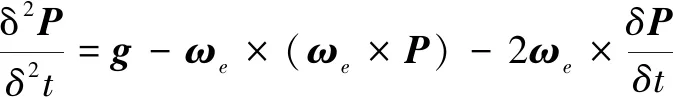
(1)

ωe为动坐标系相对惯性系的角速度,g表示引力加速度,且:

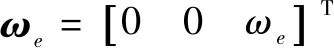
(2)

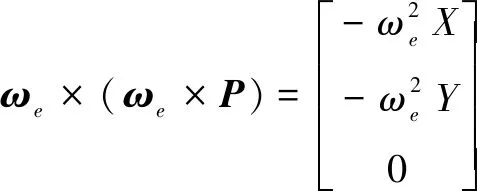
(3)

(4)

地固系下引力加速度g可表示为

(5)

飞行器自由段在地固系中的状态方程可描述为

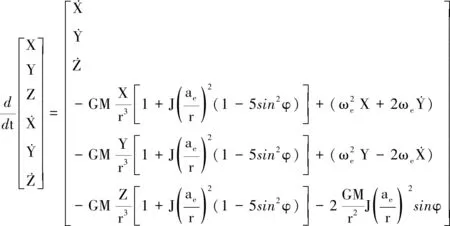
(6)

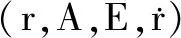
(7)

雷达站心在地固系中的位置矢量为

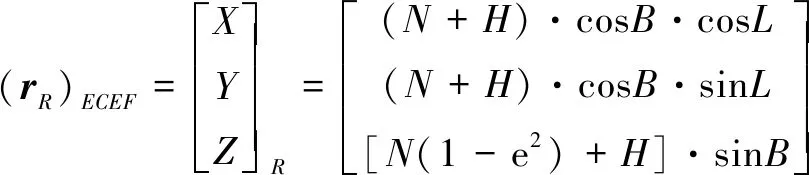
(8)

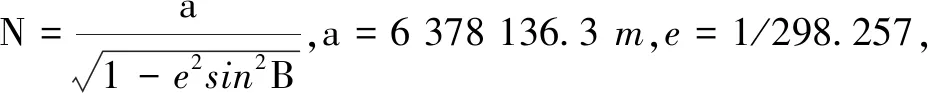
(9)

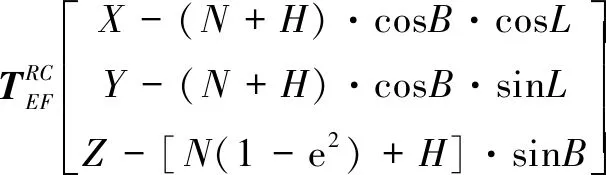
(10)

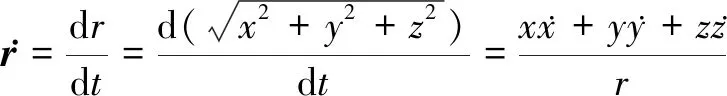
(11)

(12)

2 信息融合算法

本文所有融合方法中的主滤波器和子滤波器都是结合空间飞行器自由段运行规律,应用跟踪性能较好的UKF滤波器,具体的滤波方式可以参考文献[7]。

2.1 集中式融合算法

集中式融合是将来自多个传感器的测量数据传送到融合中心,统一完成滤波融合处理,进而对目标进行跟踪并分类。如图1,这种方法可获得较高的精度,但是数据传递和处理量大,对通信线路和处理器要求高,相对来说可靠性较差[9]。常用的集中式融合方法有并行式滤波和序贯滤波。

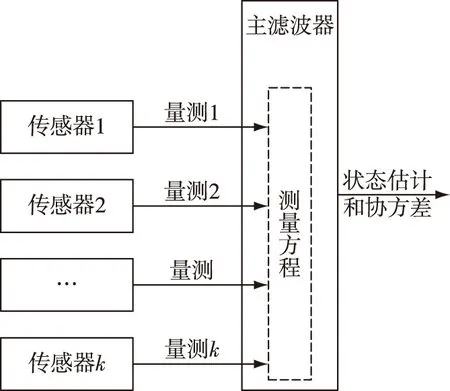
图1 集中式融合

1)基于UKF的并行式滤波

各传感器分别将量测数据传入融合中心中的主滤波器,由主滤波器通过UKF算法对全部测量数据进行融合处理。如图2,融合后输出公式:

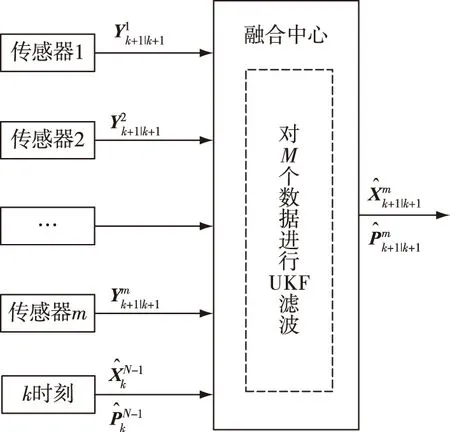
图2 基于UKF的并行滤波

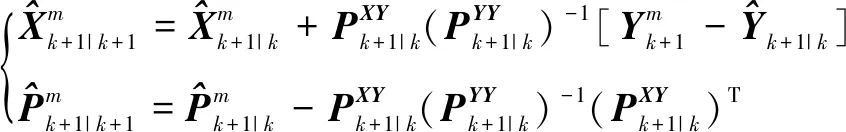
(13)

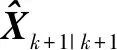
2)基于UKF的序贯滤波

基本思想是主滤波器按照从第一个到最后一个子滤波器的顺序,对目标运动状态估计值进行序贯更新,也就是通过上一时刻的一步预测,输出当前时刻的状态估计和协方差矩阵[9]。如图3,融合公式:

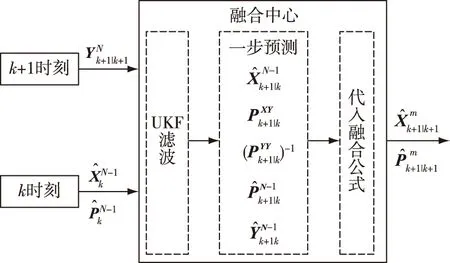
图3 基于UKF的序贯滤波

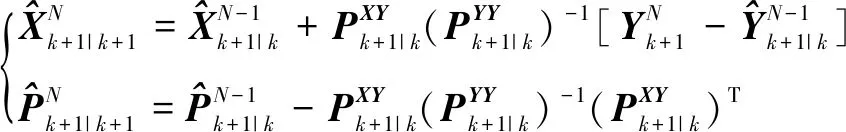
(14)

2.2 分布式融合算法

在分布式信息融合系统中局部传感器所得到的航迹称为局部航迹,融合中心融合后形成的航迹称为系统航迹也叫全局航迹[10]。如图4,在航迹进行过关联后,通过相关的规则,将航迹进行融合,通过相应的算法得到下一时刻的状态和协方差估计,完成更新。

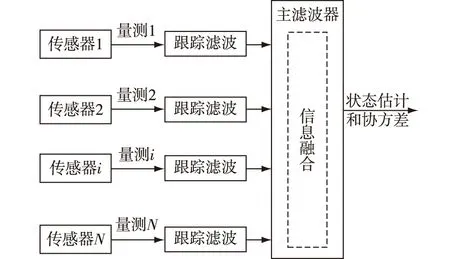
图4 分布式融合

1) 基于UKF的简单凸组合算法

假定来自不同传感器的同一目标航迹误差之间不相关,即相互独立(互协方差矩阵为0)[4]。如图5，那么N个传感器的融合结果:

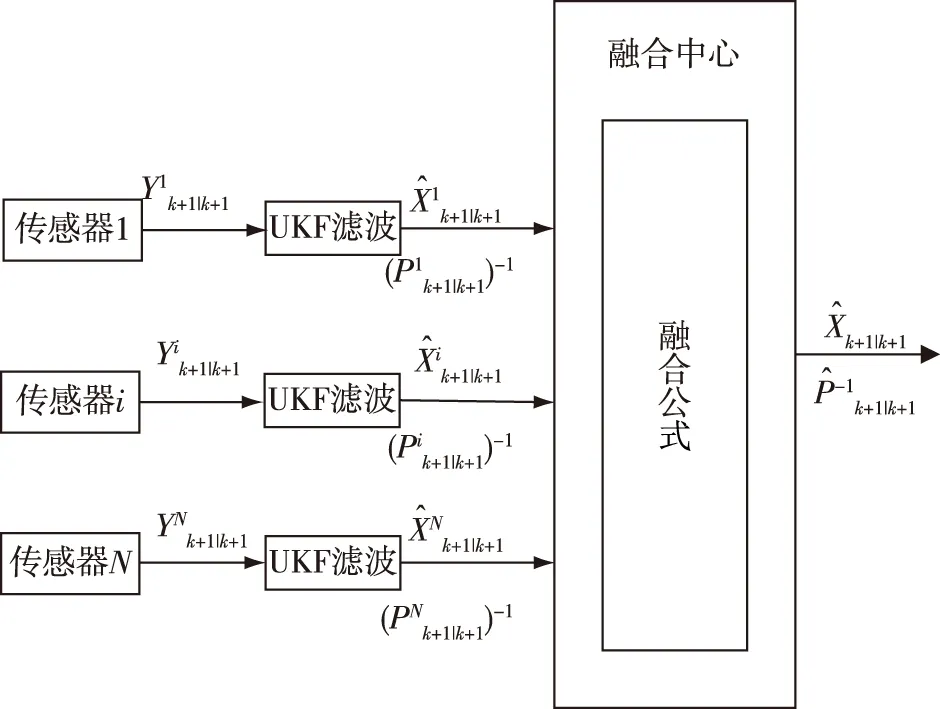
图5 基于UKF的简单凸组合融合

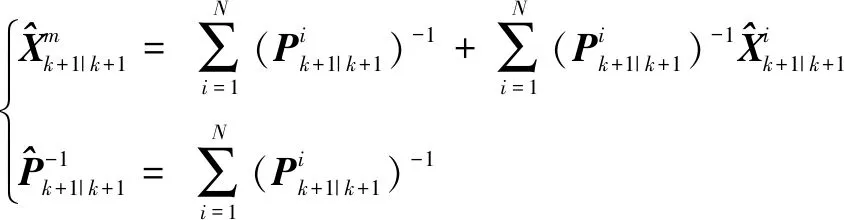
(15)

i表示第i个传感器。该算法的运算量小,在部分领域可以普遍应用。但仅有当多个局部传感器假定为不相关时才是最优算法,倘若误差相关,则退为次优算法[11]。由于凸组合融合没有考虑局部估计误差之间的相关性,轨迹跟踪的传感器之间存在较强的相关性即互协方差存在,因此该算法不适用于空间飞行器轨迹数据融合,本文不再对其进行比较。

2) 基于UKF的Bar-Shalom-Campo算法

由于凸组合考虑的条件理想,现实工程应用中很难实现传感器之间相互独立的要求,因此Bar-Shalom-Campo算法考虑了共同的先验估计或共同的过程噪声,在进行航迹融合时应考虑各传感器局部估计之间的误差相关性[12]。如图6,假设两个传感器i和j,它们在主滤波器中的融合方程及协方差阵分别为:

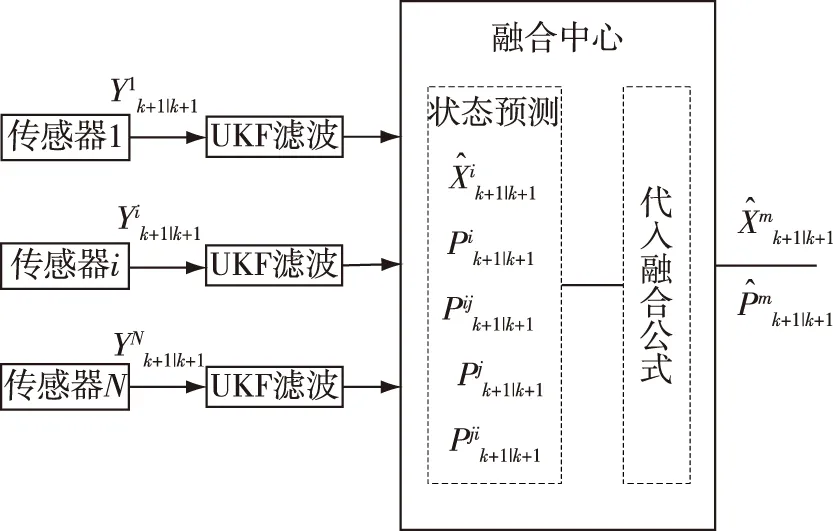
图6 基于UKF的Bar-Shalom-Campo融合

(16)

这种算法由于涉及传感器之间的协方差矩阵计算,因此需要采集大量的信息,这种方法是最大似然意义下的最优算法[10]。

3) 基于UKF的联邦滤波算法

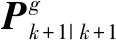
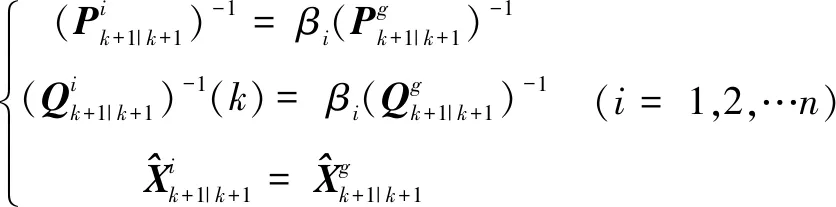
(17)

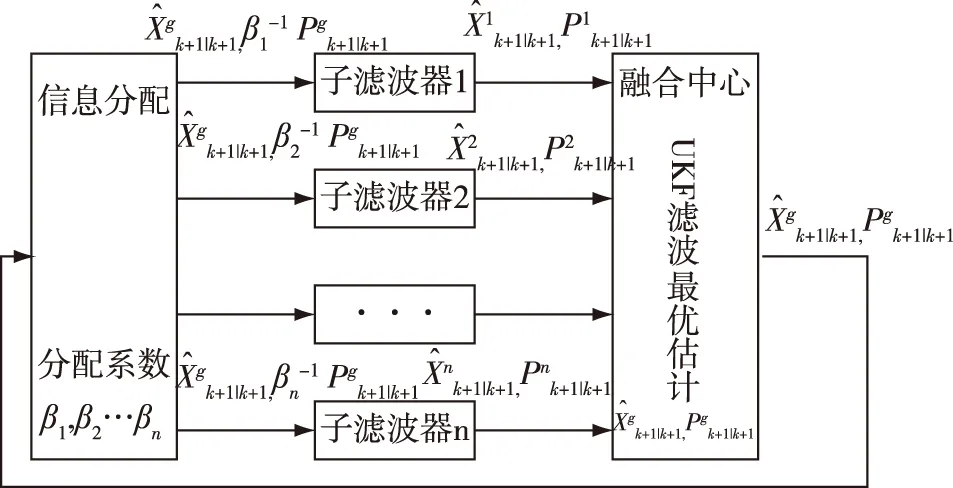
图7 基于UKF的联邦滤波融合

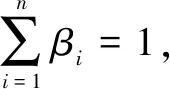
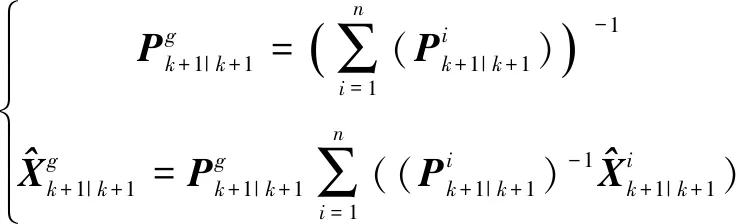
(18)

3 仿真实验与结果分析

3.1 仿真实验

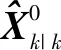
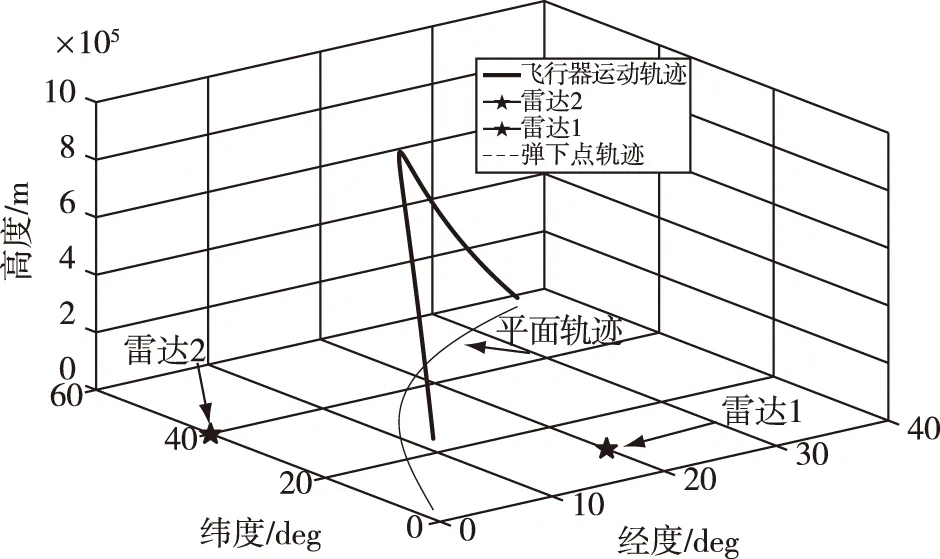
图8 雷达与飞行轨迹位置关系图

3.2 仿真结果

参考X方向位置的均方根误差,由于Y、Z方向位置和X、Y、Z方向的速度均方根误差趋势与X方向位置均方根误差趋势相近,在此不一一进行对比。表1为算法所用时间。

表1 融合滤波算法的仿真用时

1) 单雷达跟踪与另外几种融合算法的对比。由仿真结果可以看出,在飞行器自由段状态估计中,融合后滤波的均方根误差都比单雷达跟踪均方根误差要小,融合后滤波精度可得到有效的提升。这说明基于多雷达观测的信息融合对于状态估计的精度提升和对目标准确的跟踪有更好的效果。仿真结果如图9。

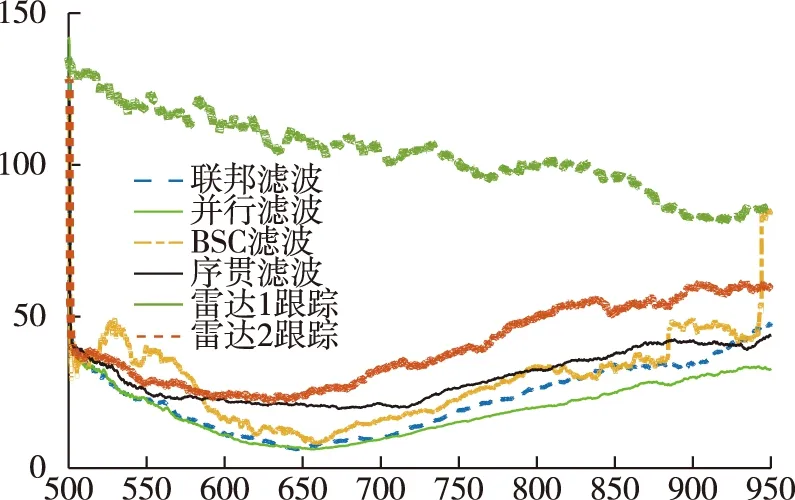
图9 融合算法与单雷达X方向位置估计均方根误差

2) 集中式融合两种算法对比。由图10可看出,在飞行器自由段状态估计中,基于UKF的并行式滤波均方根相对于基于UKF的序贯滤波均方根误差更小,计算时间更短,从精度要求来看,两者都能很好满足仿真条件要求的精度,计算量也大致相同。根据两种滤波原理可以分析得出,并行式滤波相当于对数据进行扩维滤波运算,对传感器测量误差相关性没有特殊要求,相当于对多组观测数据进行一次总的滤波,运算方式较为灵活。但如果传感器数量增加,滤波处理维数增大,尤其是在处理高维矩阵的逆等运算时计算量会相当大。而序贯滤波相当于对N个传感器进行N次的递推计算,将一步预测相关数据应用到当前的滤波器当中,虽然对于不同传感器之间具有较好的自适应性,但每次都要对当前状态进行更新,随着传感器数量增加,运算量也会随之增加。在选用集中式融合方法时,可选用并行滤波提高估计精度。根据两种融合原理分析,但如果传感器数量增加,这两种方式的计算量会增长明显,需要更宽的数据传输链路来传输原始的数据,因此在实际应用中实现起来较为困难。

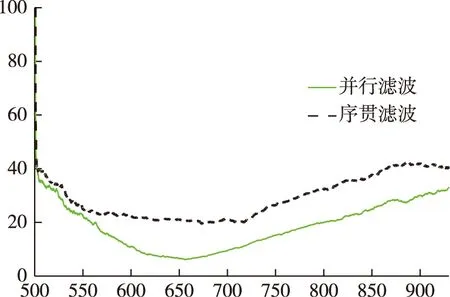
图10 并行滤波与序贯滤波X方向位置估计均方根误差

3) 分布式融合两种算法对比。由仿真结果由图11可看出,在飞行器自由段状态估计中,两部雷达观测数据下,基于UKF的联邦滤波优于基于UKF的Bar-Shalom-Campo融合滤波。Bar-Shalom-Campo融合滤波考虑了传感器误差之间的相关性,但这种方法是最大似然意义下最优估计,不是最小方差最优估计。联邦滤波之所以性能较好,是因为它利用“方差上界”技术消除了各子滤波器状态估计的相关性,各子滤波器之间实现了相互独立,然后按方差阵加权进行信息最优融合估计,得出的系统状态的估计值即为最优估计值[13]。

图11 两种分布式融合X方向位置估计均方根误差

4) 集中式与分布式融合算法的对比。选取集中式和分布式融合方式中效果最好的两个方法进行比较，即基于UKF的并行滤波和基于UKF的联邦滤波。由图12可以看出,在自由段状态估计中,基于UKF算法的并行滤波的精度要高于基于UKF的联邦滤波,但运行时间更长,两种融合方式都能较好地满足估计精度要求。在应用两部雷达进行数据融合时,若出于精度的考虑,可选用集中式并行滤波融合的方式,若出于系统容错性和计算量等方面考虑,可选用联邦滤波融合。随着传感器数量的增加,虽然集中式融合虽然能提供更准的精度,但从实际工程应用上来看,无论是出于系统容错性、稳定性考虑还是计算量等方面考虑,基于UKF的联邦滤波更适用于多传感器在自由段中状态融合估计。

图12 联邦滤波与并行滤波X方向位置估计均方根误差

4 结束语

在飞行器自由段状态估计中,多传感器信息融合确实能够提升状态估计的精度和性能。在实际应用中,若传感器数量较少时,可选用集中式融合中并行滤波的方式或联邦滤波方式进行数据融合,在传感器数量较多时,考虑计算量、跟踪时效性、系统容错性、估计精度及稳定性等相关情况,基于UKF的联邦卡尔曼滤波能够更好地进行空间飞行器自由段目标状态融合估计。