采用变时域模型预测的车辆路径跟踪控制方法

张世义， 顾小川， 唐爽， 李军

(1. 重庆交通大学 机电与车辆工程学院， 重庆 400074；2. 重庆交通大学 轨道交通车辆系统集成与控制重庆市重点实验室， 重庆 400074)

随着交通事故发生率的不断提高[1]，旨在改善交通行车环境、安全与效率的智能交通系统(ITS)正被日益推崇[2].智能交通系统集成各领域的先进技术，将人-车-路紧密配合，可以实现全局交通情况的优化与管理，对当今交通系统存在的污染、拥堵、事故频发、能源消耗过度等问题均能起到较好的缓解及改善作用.

路径跟踪通过转向轮主动转向控制准确地跟踪规划层的目标路径，并保持行车的平稳性和乘坐的舒适性[3].目前，应用较为广泛的路径跟踪算法主要采用对车辆的横向和纵向进行控制的方法，如比例-积分-微分(PID)控制算法[4]、纯追踪算法[5]、滑膜控制算法[6]、自适应控制算法[7]和模型预测控制(MPC)算法[8]等.模型预测控制算法通过预测模型、系统当前状态量和未来控制量进行在线滚动优化，再对预测输出进行矫正，从而进一步修正模型[9].由于可以处理系统多目标及多约束优化问题，MPC算法在国内得到广泛的运用.严国军等[10]提出自适应MPC控制器自动调节预测时域，减少运算时间,保证跟踪控制的实时性，但其运动学模型无法满足高速和大侧向加速度的工况.白国星等[11]基于非线性模型预测算法，采用三次多项式分别拟合速度、预测时域与稳态转向角的函数，但其运动学模型只考虑中低速的仿真效果.张严等[12]在三自由度动力学模型基础上，采用遗传算法对模型预测控制器的预测时域、控制时域进行优化，但牺牲了部分乘坐舒适性.基于此，本文提出一种变预测时域自适应路径跟踪控制方法.

1 车辆动力学模型的建立

1.1 车辆三自由度动力学模型

动力学模型和运动学模型是自动驾驶车辆建模时最常用的两种模型.运动学模型不涉及车辆自身质量、受力等因素，适用于中低车速及道路曲率、侧向加速度较小的工况；动力学模型研究车辆运行中的受力情况，通过牛顿第二运动定律建立模型方程，在高速或道路曲率较大时的效果更佳.为了提高车辆高速行驶时跟踪控制的可靠性，将车辆动力学模型作为路径跟踪研究的基础.

将车辆的三自由度模型表示为微分方程的形式，有

(1)

为了简化模型，采用小角度假设[14]，即

cosθ≈1， sinθ≈θ， tanθ≈θ.

(2)

式(2)中：θ表示轮胎的侧偏角和偏转角等角度.

当侧偏角较小时，前、后轮的侧向力与纵向力可用近似线性函数描述，前、后轮的侧向力分别为

(3)

式(3)中：Cc，f，Cc，r分别为前、后轮的侧偏刚度.

前、后轮的纵向力分别为

Fl，f=Cl，fSf，Fl，r=Cl，rSr.

(4)

式(4)中：Cl，f，Cl，r分别为前、后轮的纵向刚度；Sf，Sr分别为前、后轮的滑移率.

通过车身坐标系和大地惯性坐标系之间的转换关系，对大地惯性坐标系下车辆的运动情况进行表述，有

(5)

联合整理式(1)～(5)，简化后可得基于线性轮胎模型和小角度假设的车辆非线性连续三自由度动力学模型，即

(6)

1.2 线性化系统

将系统任意参考时刻描述为状态空间表达式的形式,即

(7)

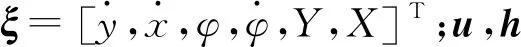
由于非线性系统不能用于线性时变模型预测控制，因此，在某参考时刻一阶泰勒展开，并结合式(7)可得误差状态方程.即

(8)

2 模型预测路径跟踪控制器

基于车辆动力学模型和模型预测控制算法，设计模型预测路径跟踪控制器.

2.1 预测方程

对误差状态方程(8)进行离散化，有

ξ(k+1)=Akξ(k)+Bku(k).

(9)

式(9)中：Ak=I+TAt，I为单位矩阵，T为采样周期；Bk=TBt；k为k时刻.

(10)

将基于MPC控制器的预测时域和控制时域分别定义为Np和Nc，Np>Nc.系统未来预测时域内的预测方程可以用矩阵形式表示，即

Y(k+1|k)=Ψkξ(k)+ΘΔU(k).

(11)

2.2 约束条件

2.2.1 轮胎侧偏角 由前、后轮侧偏角与系统各状态量的关系可知，当侧偏角不超过5°时，在任一时刻t，前轮侧偏角αf，t和后轮侧偏角αr，t的计算公式为

(12)

因此，选择前轮侧偏角的约束为-2.5°<αf，t<2.5°.

2.2.2 车辆附着条件 当车辆纵向匀速行驶时，横向加速度ay与地面附着系数μ呈线性关系，即ay≤μg.为避免约束条件限定范围过窄而求解失败，将附着条件约束设置为软约束条件，即

ay,min-ε≤ay≤ay,max+ε.

(13)

式(13)中：ε为松弛因子；ay,min，ay,max分别为横向加速度的最小值与最大值.

2.2.3 质心侧偏角β为质心侧偏角，在良好路面中，-12°<β<12°；在冰雪路面中，-2°<β<2°.

2.3 目标函数

基于MPC路径跟踪策略的目的是保证预测输出变量与参考值之间的误差尽可能小，从而准确地跟随预定的轨迹，保持跟踪稳定性.

为了求出状态方程(10)的最优解，得到控制输入增量，将其作为设计相应目标函数的状态量进行下一步求解.此外，因预测模型具有复杂性，且包含较多的动力学约束，故加入松弛因子[15]，目标函数的最终形式为

(14)

式(14)中：Q，R为权重矩阵；ρ为松弛因子的权重系数；ηref为输出量参考值.

基于以上推导过程，为便于求解，路径跟踪问题可转为二次规划求解问题，即

(15)

式(15)中：Umax，Umin分别为控制量的最大和最小值；ΔUmax，ΔUmin分别为控制增量的最大和最小值；yh，ys分别为硬约束输出和软约束输出.

2.4 反馈校正

在每一个控制周期里对式(15)完成求解计算后，得到控制时域内的控制输入增量序列为

(16)

根据模型预测基本原理，将该控制序列的首个元素值作为实际控制输入增量，再作用到系统中，有

(17)

系统不断循环向前重新预测下一时域的输出，通过优化得到新的控制序列，直至最终搜索完成.

3 变时域模型预测路径跟踪控制

3.1 车速与预测时域对跟踪效果的影响

预测时域对模型预测控制器的性能影响较大，预测时域类似于驾驶员模型中预瞄未来一段时刻的距离，在不同车速的工况下，不同的预瞄距离会产生不同的控制效果.根据以往的研究经验，当车辆低速运行时，减小预瞄距离会产生相对较好的控制效果，增大预瞄距离则会降低跟踪精度与车辆稳定性；反之，当车辆高速运行时，增大预瞄距离能够提高控制效果，且不会产生因预瞄距离过小导致的跟踪精度不良、转向抖动等问题，从而提高车辆的稳定性.搭建Carsim/Matlab/Simulink联合仿真平台，在跟踪双移线工况下，分析不同车速和预测时域的跟踪效果，车速(v)分别选取36，72，90，108，126 km·h-1，预测时域Np分别选取8，15，20，25，30；附着系数设置为0.8.

当车速为36 km·h-1时，不同预测时域的仿真结果对比,如图2所示.由于车速较低，故选取前4组预测时域数据进行对比较为合理.由图2可知：跟踪过程较为平稳，轨迹的跟踪偏差均较小，横摆角速度的变化也在合理范围内；当Np=8时，轨迹的跟踪偏差及横摆角速度最优；当Np=25时，横向位移偏差最大.

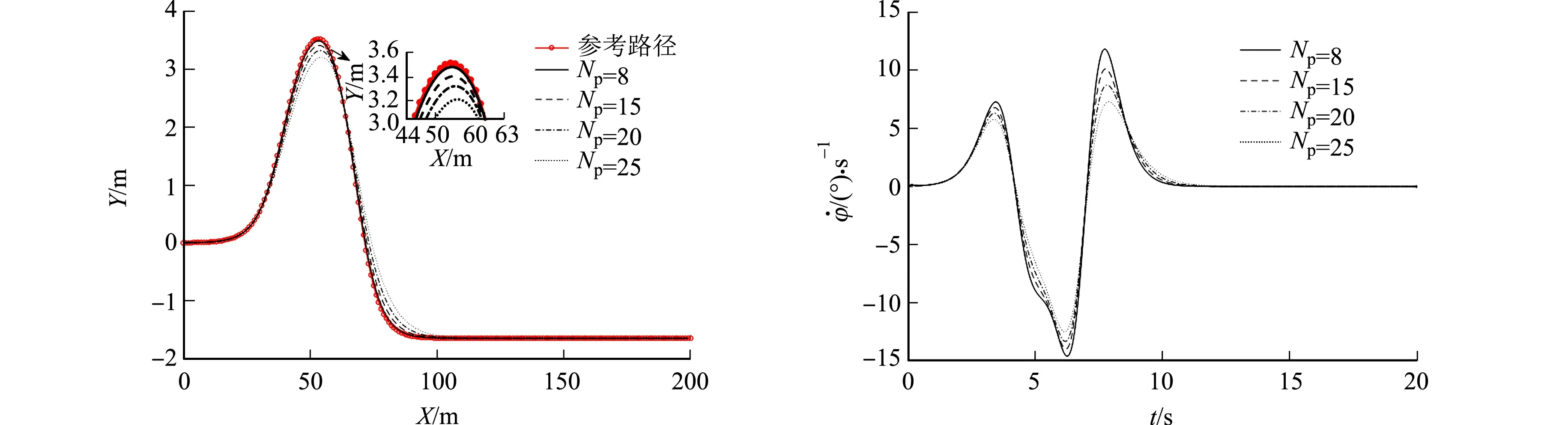
(a) 跟踪轨迹 (b) 横摆角速度图2 不同预测时域的仿真结果对比(v=36 km·h-1)Fig.2 Comparison of simulation results in different prediction horizons (v=36 km·h-1)

当车速为72 km·h-1时，选取前4组预测时域数据进行分析，不同预测时域的仿真结果对比，如图3所示.由图3可知：当Np=8时，车辆在80～100 m处再次发生侧滑，且横摆角速度过大，车辆的行驶稳定性受到很大影响，故中高车速时应该适当地增大预瞄距离，给予足够的空间响应期望轨迹；当Np=15时，跟踪偏差适中，横摆角速度的变化平滑自然，且在合理范围内.

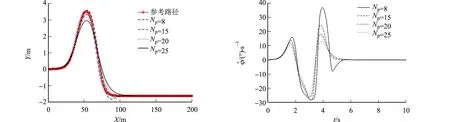
(a) 跟踪轨迹 (b) 横摆角速度图3 不同预测时域的仿真结果对比(v=72 km·h-1)Fig.3 Comparison of simulation results in different prediction horizons (v=72 km·h-1)

当车速为90 km·h-1(中高车速)时，不同预测时域的仿真结果对比，如图4所示.由于车速为72 km·h-1时，较小的预测时域会使车辆稳定性大幅降低(图3(b))，因此，在中高车速下，选取后4组预测时域进行分析较为合理.由图4(a)可知：当Np=15时，在纵向位移100 m处，横向位移偏差达到1 m，此时,横摆角速度震荡过大，表明车辆路径跟踪的稳定性较差;当Np=20时，跟踪偏差较小，横摆角速度波动平滑自然，较为合理.

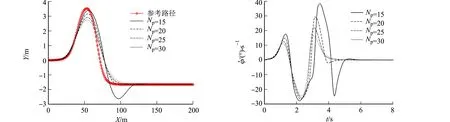
(a) 跟踪轨迹 (b) 横摆角速度图4 不同预测时域的仿真结果对比(v=90 km·h-1)Fig.4 Comparison of simulation results in different prediction horizons (v=90 km·h-1)

当车速为108 km·h-1时，选取后4组预测时域进行分析，不同预测时域的仿真结果对比，如图5所示.由图5可知：当汽车在较高车速下运行时，较小的预测时域已经无法满足路径跟踪精度和行驶稳定性的要求，这是由于高速下汽车的动力学特性发生了很大的变化，车辆行驶的稳定性急剧下降， 使车辆无法快速地响应期望的转角；当Np为25，30时，横摆角速度变化较为平稳，但当Np为30时，其路径跟踪偏差相对不理想，最大偏差达到1 m.

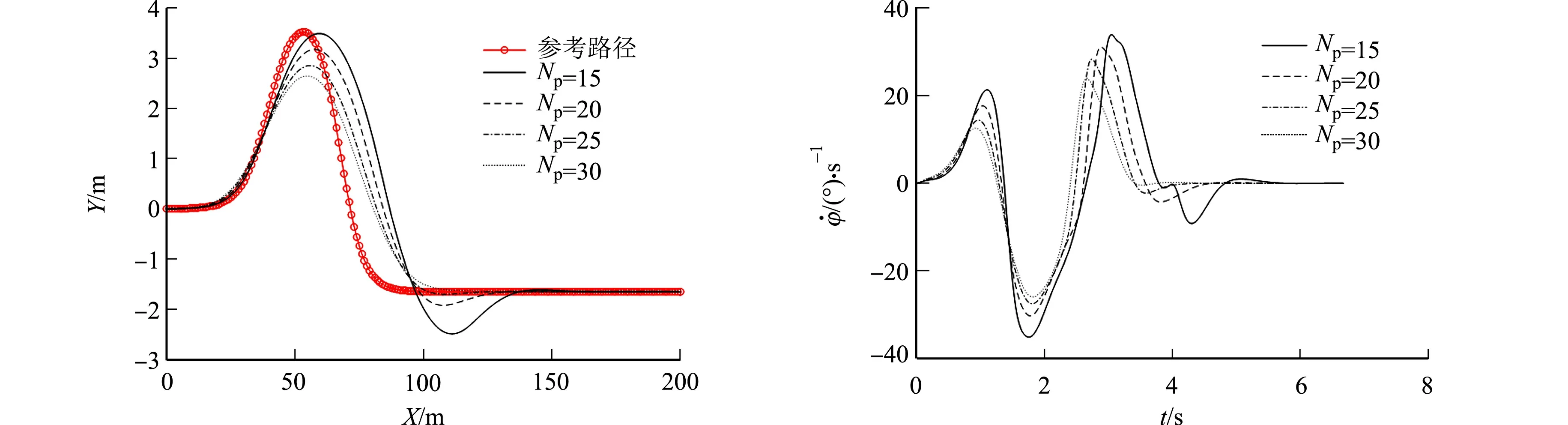
(a) 跟踪轨迹 (b) 横摆角速度 图5 不同预测时域的仿真结果对比(v=108 km·h-1)Fig.5 Comparison of simulation results in different prediction horizons (v=108 km·h-1)

当车速为126 km·h-1时，选取后4组预测时域进行分析，不同预测时域的仿真结果对比，如图6所示.由图6可知：当预测时域较小(Np=15)时，车辆的横摆角速度波动较大，已超出稳定性要求的界限，车辆严重失稳，路径跟踪失败，车辆完全脱离期望的轨迹；当Np=30时，虽然路径跟踪精度误差最大达到1 m，但由于此时车辆运行于高速工况，应着重考虑保持超车变道时的稳定性以保证安全.

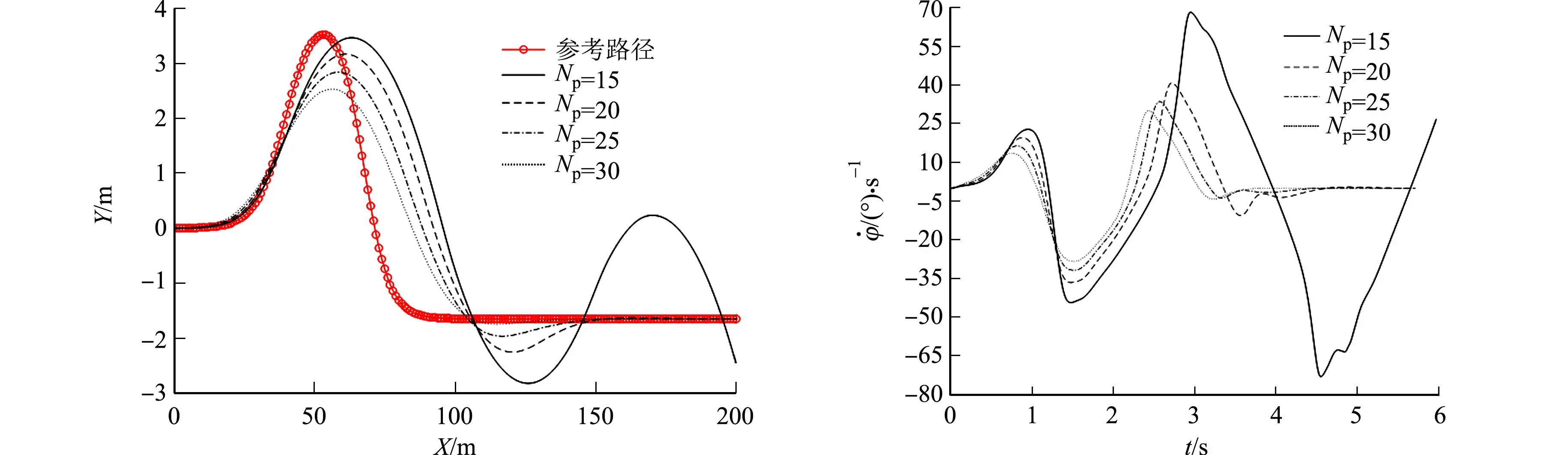
(a) 跟踪轨迹 (b) 横摆角速度图6 不同预测时域的仿真结果对比(v=126 km·h-1)Fig.6 Comparison of simulation results in different prediction horizons (v=126 km·h-1)

综上可知，在低速(某一定速)工况下，较小的预测时域的跟踪过程较为平稳，且车辆路径跟踪精度较高，而较大的预测时域会增大预瞄距离，使响应期望轨迹变慢，跟踪过程虽然平稳，但偏差相对较大；在高速(某一定速)工况下，较大的预测时域能够稳定地追踪期望路径，但由于预瞄距离增大，存在跟踪偏差，而较小的预测时域会牺牲车辆的稳定性，在高速运行时十分危险，应尽量避免.

3.2 变时域自适应路径跟踪控制器

总结预测时域与车速的变化关系，为了使车辆在不同车速下行驶时能自适应地调节预测时域，获取较优的跟踪精度及行驶稳定性，提出一种变时域自适应路径跟踪控制器，即根据车辆当前的行驶速度更新预测时域.路径跟踪控制器流程，如图7所示.

选取5组速度对应的较优预测时域作为变时域自适应路径跟踪控制器的数据来源.将数据在Matlab软件中进行3次多项式拟合，得出预测时域与车速v的拟合关系函数为

(18)

预测时域与车速的拟合函数关系曲线，如图8所示.图8中：5个圆圈代表上述对比分析后选取的实验数据.

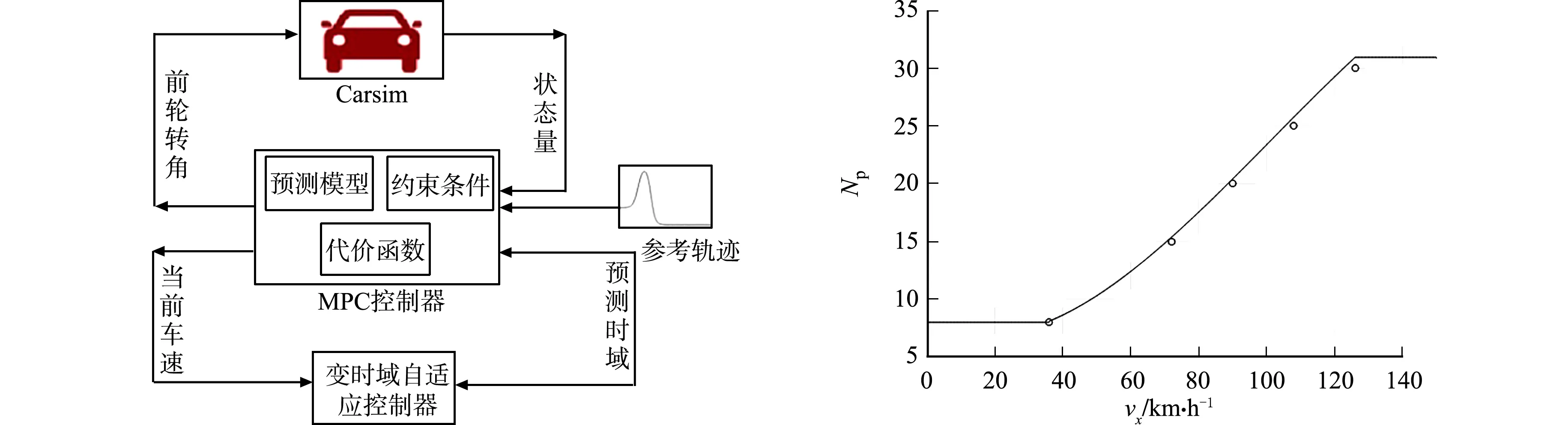
图7 路径跟踪控制器流程 图8 预测时域与车速的拟合函数关系曲线Fig.7 Flow chart of path tracking controller Fig.8 Fitting functional relation curves for prediction horizon and speed

3.3 仿真分析

设置仿真环境，对变预测时域自适应路径跟踪控制器的有效性进行验证，并与5组数据结果进行对比分析.设置附着系数为0.8，并根据车辆的实时速度不断更新预测时域，参与路径跟踪模块进行计算.变速工况下的路径跟踪仿真结果，如图9所示.

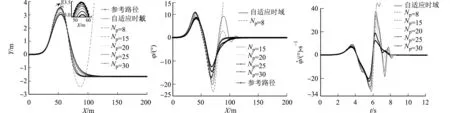
(a) 跟踪轨迹 (b) 横摆角 (c) 横摆角速度

(d) 前轮偏转角 (e) 质心侧偏角 (f) 侧向加速度

(g) 车速 (h) 预测时域图9 变速工况下的路径跟踪仿真结果Fig.9 Path tracking simulation results of path tracking under variable speed condition

由图9可知：当Np=8时，在纵向位移为80 m后，车速不断提升，此时,车辆动力学特性发生较大变化，已满足不了约束要求，控制量出现非可行解，导致在双移线工况出口处的跟踪参考路径和参考横摆角失败；预测时域较大时，跟踪精度较差，最大误差接近1 m；在自适应时域控制下，车辆能准确地跟踪参考轨迹，横摆角虽然随着车速的提升出现偏转，但是最终能迅速调整并收敛于参考值，使横摆误差趋于0，车辆恢复稳定行驶；变时域自适应路径跟踪控制器的横摆角速度变化也较为平稳，可保证车辆运行时的稳定性；质心侧偏角在±8°范围内波动，当路面附着系数为0.8时，侧向加速度也能保持在阈值范围内变化，均满足节2.2中对动力学约束的要求；随着车速的不断变化，控制器可实时更新对应的预测时域，从而预测下一时刻的输出，保证不同车速下变时域跟踪控制器良好的自适应性能.

4 结束语

建立车辆三自由度动力学模型，通过一阶泰勒线性展开，近似地离散化处理等变换，完成线性时变模型预测的理论推导.加入松弛因子，避免控制器求解过程中多约束导致非可行解的情况，进一步推导预测优化问题的矩阵形式，将模型预测路径跟踪控制问题转化为二次规划求解问题.选取不同车速及预测时域进行仿真，对比分析不同车速对应的最优预测时域值，拟合预测时域与车速的函数关系曲线，设计变预测时域自适应路径跟踪控制器，实时更新预测时域，预测下一时刻的输出值，并搭建Carsim/Matlab/Simulink联合仿真平台进行验证.结果表明：当车辆变速行驶时，自适应路径跟踪控制器在满足动力学约束的前提下，能够实时更新不同车速下的最优预测时域，并进行计算求解，在一定程度上可以解决车辆在低速和高速下的跟踪精度问题，保持车辆行驶的稳定性.