采用径向基神经网络的卫星网络申报趋势分析方法

石会鹏， 潘冀， 刘海洋， 赵睿, 刘珊杉, 韩锐

(1. 国家无线电监测中心， 北京 100037;2. 华侨大学 信息科学与工程学院， 福建 厦门 361021)

卫星频率和轨道资源是一种重要的战略资源，世界各国在使用之前需要向国际电联(ITU)进行申报和协调，其申报流程必须按照ITU的《组织法》及《无线电规则》等进行，任何一个国家都不能单方面主宰卫星频率和轨道资源的获取和使用.因此，有效地分析全球卫星网络资料的申报趋势，提前采取必要的申报策略，是抢占轨位资源战略制高点的重要前提[1].目前，我国在国际电联登记有效的卫星频率和轨道资源的资料数量已经位居世界前列.

卫星网络资料的申报是卫星频率和轨道资源获取，以及频轨战略资源储备的唯一途径.卫星网络资料的申报是一个长期过程，地球同步轨道(GSO)卫星的资源申报竞争尤为激烈[2-4].在卫星网络申报管理工作中，相关行业的专家很难准确地把握复杂的申报趋势，特别是资料的申报趋势受国际政治形势、经济态势、相关行业政策等多维度因素的影响，而大部分因素无法进行定量分析.因此，当前的卫星网络资料申报工作主要依靠专家的个人经验，缺乏量化分析的指标和方法[5].基于此，本文从卫星网络资料申报趋势预测的需求出发，将径向基函数(RBF)神经网络应用于卫星网络申报趋势分析，构建基于RBF神经网络的趋势量化分析方法.

1 卫星网络资料申报的特点

卫星网络资料申报的趋势主要分为两类：一是规划业务(planed services)；二是非规划业务(non-planed services).其中，非规划业务由于采用“先登先占”原则，竞争态势更加严峻，GSO卫星频轨资源的竞争获取尤为突出，文中主要针对非规划业务GSO卫星网络的申报趋势进行研究.

非规划业务GSO卫星网络资料申报流程，如图1所示.图1中：A,C,N资料是各国卫星网络协调的接口性文件和依据，是卫星网络申报工作的核心.A资料是卫星网络提前公布的资料，GSO卫星网络报送C资料时自动生成；C资料是卫星网络协调资料，描述卫星网络的各项指配及申报参数，如轨道参数、频率指配参数、地面站参数，以及业务和业务区等；N资料是卫星网络通知资料，进一步细化卫星网络资料参数，同时，涉及协调完成状态等.

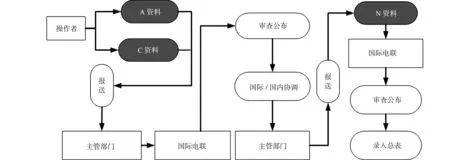
图1 非规划业务GSO卫星网络资料申报流程Fig.1 Non-planned services GSO satellite network information declaration process

此外，根据ITU的相关规定，卫星网络资料的申报不得早于其计划投入使用时间的前7年，即非规划业务频段卫星网络自国际电联收到完整申报材料之日起，须在7 a内启用，这就要求卫星网络申报工作具有前瞻性.因此，需要采用科学的预测方法，为申报工作提供量化依据.

对ITU卫星网络申报数据库中的历史申报数据进行分析可知，卫星网络的申报趋势评估主要有以下2个基本特点.

1) 评估过程具有数学回归特性.无论影响因子是连续量还是离散量，卫星网络申报趋势评估的绝大部分过程对未来趋势的发展程度均具有对应的数学模型回归的特性，时间上具有变化的延续性，可通过相应的数学模型体现出当前的发展与趋势.

2) 影响因子具有多元非线性.影响评估过程的因素非常多，因子的量化分析也极为复杂，某些因子需要通过概率统计等方式进行量化，而量化过程往往具有一定的非线性，同时，部分因子无法直接获取，可能存在隐含的相关性.

2 卫星网络申报趋势分析算法

2.1 算法的分类

对未知事物状态进行预测可采用多种算法模型，例如，朴素贝叶斯算法、K邻近聚类预测、支持向量机(SVM)和决策树等，根据各算法采用的输入向量类型进行划分，可将预测方法分为基于时间序列预测方法和基于多因子回归预测方法.

1) 基于时间序列预测方法.时间序列预测方法是给定一个历史时间序列X=(X1,X2,…,XT)，其中，T表示时间序列的长度，对未来时间序列X′=(XT+1,XT+2,…，XT+k)中的每个变量取值进行估计.按照变量取值的估计方法进行分类，时间序列预测方法可分为线性预测方法和非线性预测方法.线性预测方法主要基于统计学模型，如自回归(AR)模型、滑动平均(MA)模型和自回归滑动平均(ARMA)模型等；非线性预测方法主要指以各种人工神经网络结构为基础的预测方法，文中主要采用径向基函数神经网络进行时间序列预测.

基于时间序列预测方法是将预测目标的历史记录数据以时间为自变量，以预测对象为因变量形成时间序列，拟合出变化趋势的神经网络模型，并根据拟合模型预测目标对象的未来值，其本质是将多维度的影响因素包含在时间这个唯一的因素内[6].时间序列预测方法具有简单、直观的特点，但对于目标对象的长期预测，往往误差较大，需要不断地通过实际数据进行修正，从而获得较好的长期预测效果.

2) 基于多因子回归预测方法.基于多因子回归预测方法建立在结果与影响因素的关系上，通过研究影响预测结果的因素来预测目标对象[7].基于时间序列预测方法与基于多因子回归预测方法的区别在于前者的自变量是时间，而后者能涵盖除时间之外的多种因素.基于多因子回归预测方法能最大限度地将多种影响因素融入预测过程中，但该方法需要用户根据经验明确并量化预测具体的影响因素[8].

2.2 算法的筛选

结合上述卫星网络资料申报趋势分析过程的特点，采用基于多因子回归预测方法对卫星网络资料申报的发展趋势进行分析，往往需要设定卫星网络资料申报的影响因素，如申报卫星的轨位、频段等信息，这些信息都将对未来申报趋势的判断结果产生影响.此外，影响因子多而复杂，有些因素无法量化，例如，ITU的政策必然会影响申报趋势，但这一影响因素目前仅能凭借领域专家的直觉经验，而无公认的量化指标，故无法作为算法的输入.因此，若采用基于多因子回归预测的方法对卫星网络资料申报趋势进行分析，影响因子无法全面量化，必将增加分析方法的复杂度.

考虑到ITU数据库中存在全球卫星网络申报资料的信息，如果以单位时间周期内的资料申报数量为基准，对特定类型卫星网络资料进行统计，可以直观地表现出该类型卫星网络资料申报的变化情况.例如，按月对全球GSO卫星网络申报资料数量进行统计，可以得到以“份·月-1”为单位的资料申报数量变化曲线，该统计量是对申报趋势的直观表达.因此，采用单位时间周期内的资料申报数量作为卫星网络资料申报趋势的评价指标，不但可以直观地量化申报趋势，同时，所需考虑的影响因子也极少，仅需考虑时间这一维度.综上，采用基于时间序列预测方法对卫星网络申报趋势进行分析.

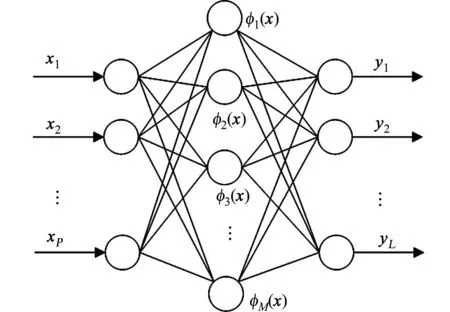
图2 RBF神经网络结构Fig.2 RBF neural network structure

2.3 RBF神经网络预测算法

在面向时间序列的预测方法中，人工神经网络算法是一种有效的预测算法.目前，人工神经网络的结构设计主要是受生物学原理的启发，但有一类神经网络模型的建立是基于数学原理的指导，RBF神经网络是典型的代表.目前，大部分传统人工神经网络的应用都是基于反向传播(BP)神经网络，但BP神经网络具有局限性，容易陷入局部极小值，而RBF神经网络因其结构特点而具有更好的函数逼近能力，能有效地克服BP神经网络的部分缺陷[9].RBF神经网络是一种前馈神经网络，仅有3层网络结构，如图2所示.图2中：X=(x1,…，xP)为网络的输入向量；Y=(y1,…，yL)为网络的输出向量;而φ1(X)～φM(X)为激活函数(一般采用高斯函数).

由于RBF神经网络各层使用的激活函数与BP神经网络不同，因此，RBF神经网络的逼近性能更好.此外，采用局部激活函数的RBF神经网络能在很大程度上克服BP神经网络容易陷入局部极小值的问题，并且在网络结构设计上可以更好地采用量化分析方法，而不是依赖设计人员的经验，训练效率也较BP神经网络更高[10-12].采用RBF神经网络的文中算法设计如下.

1) 网络结构设计.RBF神经网络的结构设计方法一般有聚类算法、梯度训练方法和资源分配网络(RAN) 算法[13].因资源分配网络算法具有较好的训练效率，故将其作为RBF网络结构设计算法，具体有以下5个步骤.

步骤1设置网络输出误差期望值D(不同应用可根据样本拟合情况进行调整).

步骤2引入2个训练样本数据，对隐层节点中心和权值进行初始化赋值.

步骤3再输入1个样本数据，计算网络输出，如果网络输出符合新颖性要求，则引入该节点，新颖性的定义是新输入的样本点需满足两个条件，即

(1)

(2)

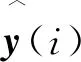
步骤4若新输入的样本数据不符合新颖性要求，则采用最小均方(LMS)算法调整中心和权值.

步骤5循环执行步骤3，4，直到所有样本输入完成，或网络输出误差小于预测值D时，完成网络结构设计[15-17].

2) 样本集预处理.从上述网络结构设计可以看出，样本数据对网络结构的设计有直接的影响.因此，科学地选取和处理样本，可有效提高分析结果的准确性.根据卫星网络资料申报的特点，采用时间序列形式的样本数据.为了使卫星网络资料的样本数据可以被RBF神经网络识别，需对样本数据进行样本序列化、数据清洗和队列抗劣，具体有以下3个步骤.

步骤1样本序列化.采用单位时间周期内的资料申报数量(如份·月-1)作为卫星网络资料申报趋势的评价指标，在相关数据库中，按照待预测的卫星网络资料类型(如全球GSO卫星网络或Ka频段卫星网络等)进行统计，获得以份·月-1为单位的卫星网络资料统计值，并对申报时间进行自然数序列化处理，将其作为算法模型的输入.

步骤2数据清洗.由于ITU等数据库中统计的样本数据时间跨度较长，以全球GSO卫星网络N资料申报趋势预测为例，在数据库中，该类资料在1990年前已有记录，但在实际使用中，跨度过长的历史数据样本会造成更大的误差，产生过拟合现象.为减少久远的历史数据样本对当前趋势产生过拟合的影响，经过对不同样本数据的迭代计算可知，以趋势预测时间点前9年的数据作为样本的效果最好.

步骤3队列抗劣.由于卫星网络申报资料的样本不可避免地受到短时波动因素的影响，该类影响并不是卫星网络资料申报趋势的主要内因，且会对样本数据产生噪声.因此，采用最小二乘平滑(OLS)对样本进行抗劣去噪处理，具体流程如下.

输入：样本集合(Zi,Ki),Zi为序列索引号，Ki为待预测类型的卫星网络资料的每月申报数量，i取值为[1,n],n为样本项目数量.

输出：输出抗劣去噪后的新样本集合Oi.

Ⅰ) 按照一定尺度m开辟先进先出(FIFO)队列滑动窗口为[(Z1,K1),(Z2,K2)，…，(Zm,Km)].

Ⅱ) 将该窗口从样本时间序列的前端开始滑动，每滑动一次样本点，就进行一次最小二乘拟合计算，即获得多项式方程φ(Z)=α0+α1Z+…+αlZl，使窗口内各样本点与其偏差σ的平方和最小，即

Ⅲ) 按多项式方程φ(Z)计算新样本点的Ki值.

Ⅳ) 重复Ⅱ)，Ⅲ)，直至处理完所有样本点，生成新样本集合Oi.

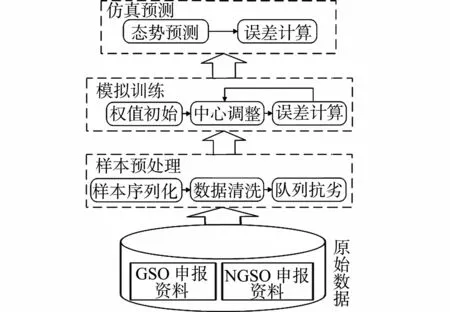
图3 申报趋势预测流程Fig.3 Declaration trend forecasting process

用预处理后的样本对网络模型进行训练，即可得到卫星网络申报趋势预测的RBF神经网络模型.申报趋势预测流程，如图3所示.

3 分析方法与验证

卫星网络资料申报状态的统计及申报趋势发展的预测评估可以指导相关部门或卫星操作者进行判断.主要评估集有卫星网络资料数量的增长趋势、GSO轨道资源的竞争趋势和非对地静止轨道(NGSO)资料的增长趋势等.按照节2的算法，以ITU数据库2008-2016年的卫星网络申报数据为训练集，以2017年的申报数据为测试集，构建申报趋势的RBF神经网络预测模型，并对模型进行测试验证.以2017年1月全球GSO卫星网络N资料申报的趋势预测为例，进行算法验证.

1) 样本序列化.根据ITU数据库的查询规则，从数据库中提取全年的N资料，按照资料申报时间，按月份进行统计，以2016年上半年为例，得到以份·月-1为统计单位的全球卫星申报N资料数kN(表1).对“年-月”字段进行序列化(表2)，以自然数序列代替“年-月”的形式，因为神经网络的输入节点一般要求为连续或离散的数值形式.

表1 N资料库表

表2 序列化后N资料库表

在程序中导入序列化后的库表数据，以序列化后的时间为横坐标，以GSO卫星网络N资料每月申报数为纵坐标，可得申报资料统计曲线(1986-2018年)，如图4所示.

由图4可知：在序列号270(2008年)附近产生了申报趋势上的变化，这是由于申报趋势的影响因素(如商业航天兴起)发生了变化，为减少历史数据造成的过拟合，增加影响因素变化后的样本数据比重，需对样本数据进行清洗.

2) 数据清洗.以9年为一组数据进行数据清洗，对2017年1月GSO卫星网络N申报数量进行预测，即以2008年6月为起点，以2016年12月为终点，统计GSO卫星网络N资料申报情况，可得申报资料统计曲线，如图5所示.清洗后样本数据序列号(2016上半年)也相应地发生变化，如表3所示.

图4 N资料统计曲线(1986-2018年) 图5 数据清洗后的N资料统计曲线(2008-2016年) Fig.4 Statistical curve of N data (1986 to 2018) Fig.5 Statistical curve of N data after data cleaning (2008 to 2016)

3) 队列抗劣.由于样本存在噪声，需对样本数据进行队列抗劣处理，结果如表4所示. 截取2008年6月至2016年12月的数据作为RBF网络模型的训练样本，队列抗劣后的样本，如图6所示.

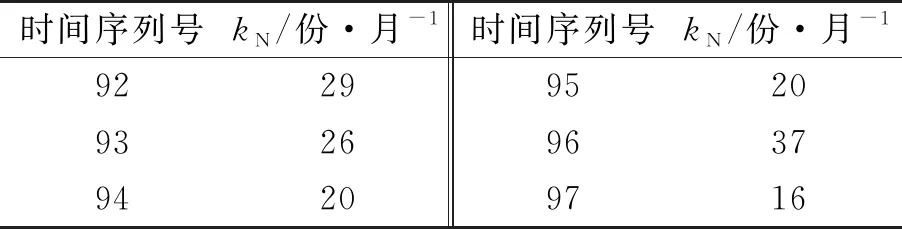
表3 数据清洗后的数据示意表

表4 队伍抗劣后的数据示意表

4) 网络初始化.完成数据样本的采集后，可以开始RBF神经网络结构的设计，RBF网络结构的构建采用资源分配网络学习算法.

5) 中心调整.首先，选取两个输入样本，将其作为RBF神经元的结构参数代入网络结构中，得到相应的输出结果；然后，重新设计网络线性层，逐步减小误差.

6) 误差计算.如果网络输入误差未达到预期值，则根据下一个最大误差的样本，再增加一个神经元，如此反复，使误差减小，直至误差达到规定的误差性能，或神经元数量达到上限时，整个建网结束.

RBF神经网络模型对样本集的拟合曲线，如图7所示.该模型在完成100次反向传播训练后，模型训练的均方误差为0.015 4.

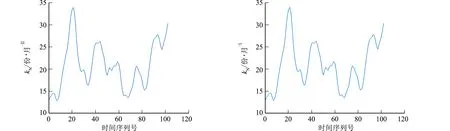
图6 队列抗劣后的样本 图7 RBF神经网络模型对样本集的拟合曲线 Fig.6 Sample after anti-inferior of queue Fig.7 Fitting curve of RBF neural network model to sample set

7) 趋势预测.获得训练后的RBF神经网络模型后，输入序号103(2017年1月)可得2017年1月全球GSO卫星网络N资料申报趋势预测为22.4份·月-1.

8) 误差对比.2017年1月实际统计的全球GSO卫星网络N资料申报为19份，与预测结果22.4份·月-1对比，相对误差约为18%.

按照申报趋势的预测流程，选取对应的样本集，重复计算，可得2017年GSO及Ku/Ka波段等卫星网络N资料的预测验证结果，如表5所示.表5中：kN,f为N资料数的预测值；kN,r为实际值；η为误差.

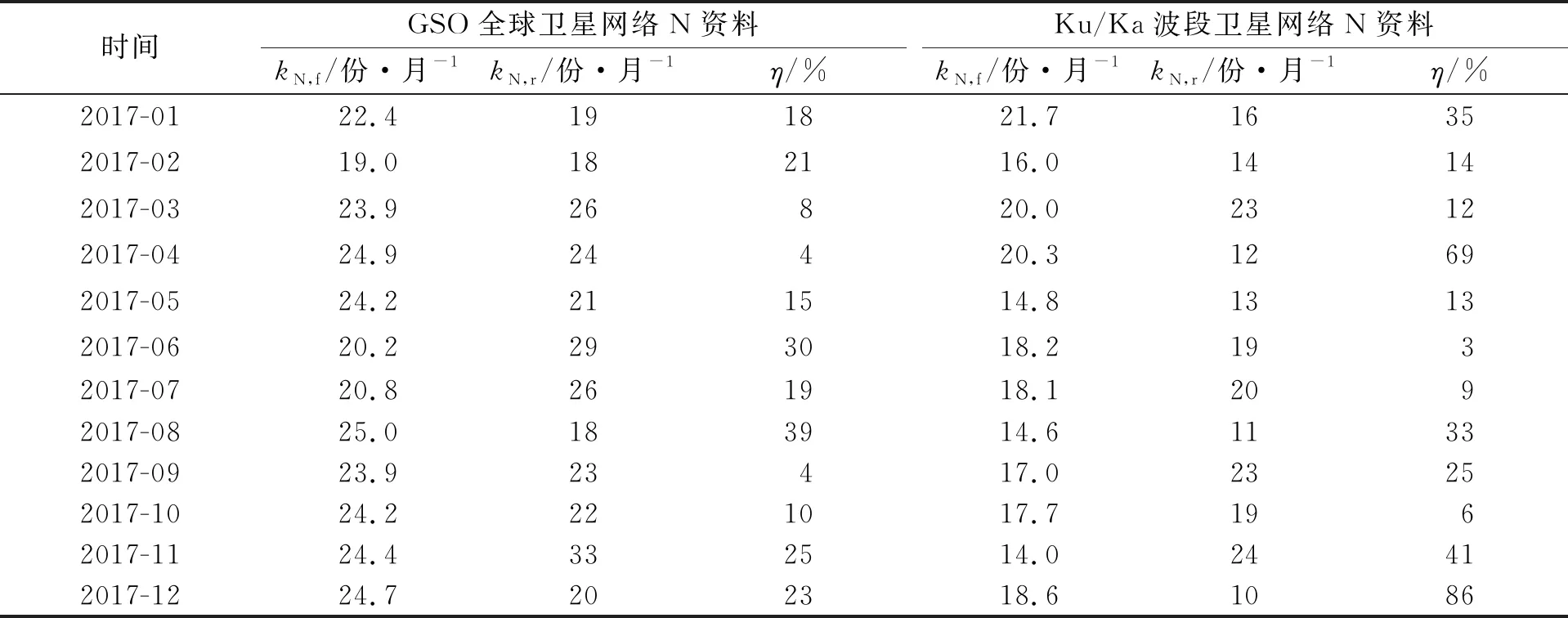
表5 预测验证结果Tab.5 Forecast verification results

(3)

式(3)中：ηi为第i月的预测误差值.

将表5的误差数据代入式(3)，可得GSO全球卫星网络N资料2017年月平均误差约为18%.

4 结束语

基于RBF神经网络算法构建卫星网络资料申报趋势的预测模型,结合真实的历史申报数据进行实验验证.结果表明：GSO全球卫星网络N资料单月预测结果误差基本小于20%，全年平均约为18%，准确度较高，验证了该模型的有效性与评估效能，而Ku/Ka波段等卫星网络N资料中部分误差较大的月份也可为频率协调操作者提供有针对性的申报趋势影响因素的分析方向.