SH 波入射下圆弧状沉积盆地地震反应瞬态解析解计算1

任 朋 陈三红 张郁山

1）中国地震局地球物理研究所，北京 100081 2）中国地震灾害防御中心，北京 100029

引言

强震动观测和震害调查结果均表明，沉积盆地对地震动（尤其是长周期地震动）具有放大效应。基于数值解的盆地效应研究涉及大规模数值计算，尤其是针对较大尺度的盆地。具有规则几何形状的地层结构对地震波散射问题的解析解可用于验证数值计算结果精度，是研究局部场地、地形和盆地对地震动参数放大效应影响的重要理论工具。针对沉积盆地对地震波散射问题，Trifunac（1971）、Wong 等（1974）分别利用波函数Fourier-Bessel 级数展开法和Mathieu 级数展开法，在频域内给出了半圆形和半椭圆形沉积盆地对SH 波散射问题的解析解。针对具有不同深度与宽度比的浅圆形沉积盆地，Todorovska 等（1991）提出了近似的解析解，即利用半径非常大的圆弧近似模拟水平地表，该方法进一步被拓展应用于该类盆地对P 波、SV 波和Rayleigh 波的散射问题（梁建文等，2001，2003，2006；李伟华等，2004；Li 等，2005）。针对浅圆形沉积盆地对SH 波的散射，Yuan 等（1995）提出了闭合形式的级数解，有效避免了大圆弧的近似假定。通过利用大圆弧面近似模拟水平地表，梁建文等（2009a，2009b，2010）求解了三维空间中沉积谷地对P 波、SV 波和Rayleigh 波的散射问题。

上述解析解均在频域内给出，可较好地研究沉积盆地对地震动Fourier 谱分量的放大效应，但工程中更关注地震动时域参数，如峰值加速度（PGA）、峰值速度（PGV）和峰值位移（PGD）及反应谱等。理论上，利用频域稳态解和Fourier 变换，易获得时域瞬态解析解，从而获得地震动时域参数。但上述研究中地震波频率参数η（盆地宽度与入射波波长比值）≤10.0，无法满足获取可靠瞬态解的要求，如对于宽度1 km 的盆地，假定介质剪切波速为1 km/s，如果输入地震动离散时间间隔为0.01 s，则其Nyquist 频率为50 Hz，所需η将高达50。针对该问题，张郁山（2010）提出无须求解线性方程组的级数解法，有效拓展了沉积盆地对SH 波散射问题解析解适用的频带范围。基于张郁山（2010）的研究，本文利用Fourier 变换，获得该问题的瞬态解析解，并研究了El Centro 波入射下，沉积盆地对地震动参数（尤其是长周期参数）的放大效应。

1 瞬态响应解析解

本文首先给出圆弧状沉积盆地在平面SH 波入射下瞬态响应解析解。沉积盆地模型如图1 所示。盆地边界为浅圆弧，其圆心为O1点，半径为b，盆地半宽为a，深度为h，圆心O1与地表之间的垂直距离为d。盆地内沉积介质剪切波速为cv，密度为 ρv，剪切模量µv=ρvc2v。半空间介质剪切波速为cs，密度为 ρs，剪切模量µs=ρsc2s。所有介质假定为均匀、线弹性和各向同性。以圆心O1为原点的坐标系直角坐标为x1和z1，极坐标为r1和 θ1，以盆地地表中心点O2为原点的坐标系直角坐标为x2和z2，极坐标为r2和 θ2。Vi和Vr分别为入射和反射SH 波， γ为入射（反射）角，Vv为 盆地内散射波，Vs为半空间外行波。

图1 沉积盆地模型Fig. 1 Model of alluvium basin

假定入射SH 波幅值为1、圆频率为ω ，稳态条件下，其时间因子为exp(−iωt)，其位移幅值在x2O2z2坐标系下表达式为：

在以O1为极点、θ1为极角、r1为极径的极坐标系下，整个自由场位移Vi+r=Vi+Vr可表示为Fourier-Bessel 级数形式（Abramowitz 等，1972）：

2 结果分析

本文引用稳态级数解的收敛项数，随着无量纲频率η的增大而增加，如对于深度与半宽比为1/2 的盆地，当η=2时，收敛项数为26，当η=20时，收敛项数为157（张郁山，2010）。在本文考虑的频带范围内，稳态级数解均能有效收敛，从而保证了瞬态动力响应计算结果可靠。基于该瞬态动力响应的解析解，本文进一步研究沉积盆地对各类时域地震动参数的放大效应，重点讨论空间位置、入射角、几何参数和物理参数等对盆地放大效应的影响。

2.1 盆地不同空间点放大效应及入射角的影响

以某一特定盆地为例，分析盆地不同空间点处地震动参数放大效应的差异，并讨论SH 波入射角对盆地放大效应的影响。

盆地半宽为500 m，深度为250 m，沉积介质剪切波速和质量密度分别为750 m/s和2 000 kg/m3，半空间介质剪切波速和质量密度分别为1 000 m/s和2 200 kg/m3。参考点坐标设定为（−1 500 m,0 m），该点处自由场运动假定为以0.2g标定的El Centro 波，其加速度、速度和位移时程曲线分别如图2（a）、3（a）、4（a）所示。SH 波垂直入射条件下（γ=0°），图1 所示盆地地表中心点（0,0）处地震反应分别如图2（b）、3（b）、4（b）所示，边界点（500,0）处地震反应分别如图2（c）、3（c）、4（c）所示。由图2～4 可知，盆地中心点地震动PGA 放大效应不明显，放大系数仅为1.05，PGV 和PGD 放大系数分别达1.30和1.21；盆地边界点地震动反而有减小趋势，PGA 放大系数为0.75，PGV 和PGD 与入射波相近。

图2 自由基岩、盆地中心点和边界点地震动加速度时程曲线Fig. 2 The time history curve of ground motion acceleration of free bedrock, central point and boundary point of basin

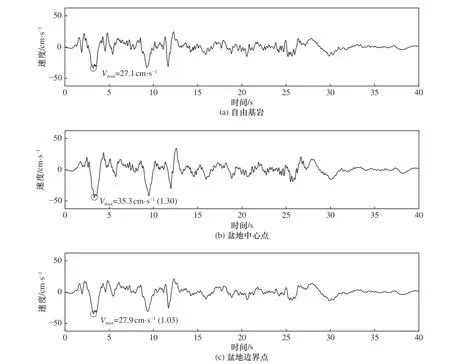
图3 自由基岩、盆地中心点和边界点地震动速度时程曲线Fig. 3 The time history curve of ground motion velocity of free bedrock, central point and boundary point of basin

图4 自由基岩、盆地中心点和边界点地震动位移时程曲线Fig. 4 The time history curve of ground motion displacement of free bedrock, central point and boundary point of basin

该盆地不同地表点地震动反应谱（阻尼比为5%）与自由场地震动反应谱之间的谱比曲线如图5 所示。图5 中，实线表示盆地内部点结果，点线表示盆地外部点（盆地外部点范围为500 ＜|x2|＜1 000）结果，红色粗实线表示盆地中心点结果。由图5 可知，盆地中心点谱比最大值达1.57，其对应的周期TP=0.24 s（本文将其定义为卓越周期），且该谱比曲线在＞1.0 s的周期范围出现1 个放大系数接近1 .6的较大峰值点。当周期为0.24～1 s 时，盆地内部大部分点谱比均＜1 .0，盆地外部大部分点谱比＜1 .0。

图5 垂直入射下盆地地表地震动反应谱谱比曲线簇Fig. 5 The spectral ratio curve cluster of ground motion response spectrum under vertical incidence

不同入射角条件下（γ=0°, 30°, 60°, 90°）盆地地表地震动参数放大系数空间变化曲线如图6 所示。由图6 可知，在垂直入射条件下，盆地内部点具有较显著的放大效应；在斜入射条件下，盆地对地震动的放大更多出现在背波面（x2＞0），且主要分布在盆地边缘附近。

图6 不同入射角下地震动参数放大系数空间变化曲线Fig. 6 The spatial variational curve of ground motion parameters amplification factor at different incident angles

2.2 盆地特性对放大效应的影响

以SH 波垂直入射条件下，盆地地表中心点地震动参数放大系数为指标，分析盆地自身动力特性对放大效应的影响，重点讨论盆地尺度、沉积层厚度和介质力学参数等因素的影响。其中，自由场地震动依然假定为El Centro 波，参考位置为盆地左侧距中心点3倍盆地半宽处。

2.2.1 盆地尺度

将盆地半宽由0.5 km增至5 km，盆地深度始终取为半宽，盆地内、外介质剪切波速分别取为1.5 km/s和2.5 km/s，质量密度分别取为2 100 kg/m3和2 300 kg/m3。不同宽度盆地地表中心点处地震动PGA、PGV 和PGD 如图7 所示，由图7 可知，半宽＜0.76 km的较小尺度盆地对PGA 放大效应明显，放大系数高达2.13；半宽为1～1.57 km的中小尺度盆地对PGV 放大效应较显著，放大系数高达1.89；半宽＞1.6 km的较大盆地对PGD 放大效应显著，放大系数高达1.83，这是因为盆地尺度越大，其对长周期地震波的放大效应越强，而地震动PGD 受长周期成分控制。

图7 地震动峰值放大系数与盆地宽度关系曲线Fig. 7 The relationship curve between the peak amplification factor of ground motion and the width of basin

小盆地（半宽0.5 km）和大盆地（半宽5 km）地表中心点地震动与自由基岩地震动相对位移反应谱曲线如图8（a）所示，小盆地（半宽0.5 km）和大盆地（半宽5 km）地表中心点地震动谱比曲线如图8（b）所示。由图8（a）、8（b）可知，小盆地对地震动反应谱的放大效应主要出现在周期＜1.64 s，其在极高频处的谱比高达2.15；周期＞1.64 s时，大盆地对长周期反应谱具有显著的放大效应，谱比高达2.31，对于位于较大型盆地上的基本自振周期较长的工程结构，对结构变形和承载力提出更高要求，结构抗震分析应重视该类放大效应。谱比曲线卓越周期与盆地半宽的关系曲线如图8（c）所示，谱比最大值与盆地半宽的关系曲线如图8（d）所示，由图8（c）、8（d）可知，随着盆地尺度的增大，卓越周期有增大趋势，谱比最大值在大部分情况下＞2 .0。

图8 盆地宽度对其放大效应的影响Fig. 8 The effect of basin width on its amplification

综上所述，盆地尺度对地震动参数放大效应具有显著影响，这种放大效应在实际工程中应引起足够重视，尤其是对于位于大型盆地上的超高层建筑、大型储液罐和大跨度桥梁等结构，其抗震分析应充分考虑盆地对长周期地震动参数的放大效应。

2.2.2 盆地沉积层厚度

盆地半宽取为1 km，沉积层介质和半空间介质力学参数与前文相同，沉积层厚度由0.4 km增至1 km （即半圆形盆地），不同地震动参数放大系数与沉积层厚度关系曲线如图9（a）、9（b）所示。由图9（a）、9（b）可知，对于较小型盆地，沉积层厚度对中长周期地震动参数（PGV 和1.0 s 反应谱）和长周期地震动参数（PGD 和6.0 s 反应谱）放大系数的影响较小，高频地震动参数（PGA 和0.1 s 反应谱）放大系数随沉积层厚度的变化较剧烈，但未呈现单调变化趋势。其他参数不变，盆地半宽取为5 km、沉积层厚度由2.5 k m增至5 km，不同地震动参数放大系数与沉积层厚度关系曲线如图9（c）、9（d）所示。由图9（c）、9（d）可知，随着盆地尺度的增大，沉积层厚度对中长周期和长周期地震动参数放大效应的影响逐渐显著，其对长周期地震动参数的放大效应显著高于小盆地。

图9 不同盆地宽度条件下深度对地震动放大系数的影响Fig. 9 The effect of depth on ground motion amplification factor under different basin widths

2.2.3 盆地沉积介质剪切波速

盆地半宽取为1 km，沉积介质厚度取为0.5 km，半空间剪切波速和质量密度分别为2.5 km/s和2 300 kg/m3。沉积介质质量密度统一取为2 100 kg/m3，其剪切波速由1.3 km/s增至2.3 km/s。不同地震动参数放大系数与沉积介质剪切波速关系曲线如图10 所示。由图10 可知，随着沉积介质剪切波速的增大，地震动参数放大效应呈减小趋势，这是因为沉积介质剪切波速越小，沉积介质与下卧半空间介质之间的阻抗比越大，在二者交界面处，将有更多的下行地震波反射至盆地内部，盆地内散射波复杂的干涉效应将造成地表地震动更大的放大效应。

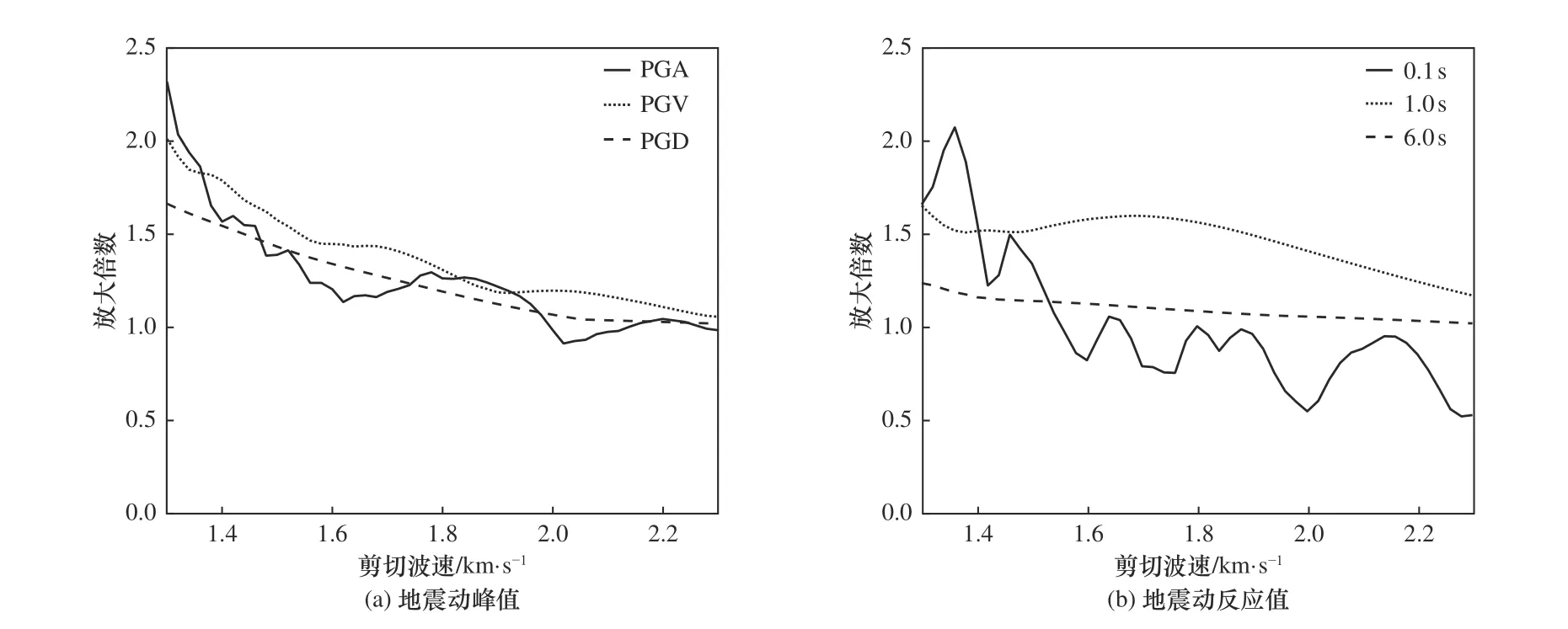
图10 盆地沉积介质的剪切波速对地震动放大系数的影响Fig. 10 The effect of shear wave velocity of alluvium medium on ground motion amplification factor in basin

3 结论

本文基于SH 波入射下沉积盆地动力响应宽频带稳态解析解，利用Fourier 变换，得到瞬态解析解，并研究沉积盆地对地震动参数的放大效应，得出以下结论：

（1）盆地对地震动参数的放大主要发生在盆地内部，相比自由基岩地震动，盆地外部一定范围内地表地震动反而出现减小现象，且在斜入射条件下，盆地对地震动参数的放大区域主要出现在背波面。

（2）盆地尺度对地震动参数放大效应具有显著影响，随着尺度的增大，谱比曲线卓越周期增大，且大尺度盆地对长周期反应谱的放大系数高达2.31。因此，进行位于大型盆地上的超高层建筑、大型储液罐和大跨度桥梁抗震设计时，应充分考虑盆地放大效应对设计地震动参数的影响。

（3）盆地沉积层厚度和沉积介质剪切波速均对地震动参数放大效应具有一定影响。此外，本文仅考虑El Centro 波输入下的盆地效应，事实上，输入地震动不同时会对分析结果产生一定影响。因此，建立盆地地震动参数放大效应工程评估模型时，应综合考虑多因素的不确定性对模型的影响。