巧用自变量找到解题的突破口
2021-04-14陈清
陈 清
(广西南宁市第十三中学 530011)
物理作为研究物体发展和变化规律的一门学科,是以客观事物为基础,探究事物发展的方向,并利用其中的规律去解决发展中存在的问题,而事物的发展总是以一定的顺序来进行的.所以,在高中物理教学中,我们要善于利用事物发展的一些规律,以某个量为“自变量”,让其因变量自动呈现出来.从而培养学生发现问题,解决问题的能力和良好的思维方法,下面,我从四个方面来举例说明:
一、以时间为轴,分析物体的运动
物体的运动和发展绝大部分是以时间为线,按照时间的先后发生为序,所以,我们在分析物理过程时,可以以此为线,帮助学生学会分析物理过程,找到问题所在,然后利用所学知识,解决问题.
例1一辆汽车从A点由静止开始运动,开始做加速度为3m/s2的匀加速直线运动,运动了8s到达B点,然后立即以5m/s2的加速度大小做匀减速直线运动,直至运动到C点停止运动.求:
(1)汽车运动至B点时,物体的速度是多少?
(2)汽车减速运动持续了多少时间?
(3)汽车运动的总位移是多少?
这类问题就是以事情的发生先后为线,我们上课时只要以时间为“自变量”,教会学生画运动草图来分析物体的运动过程,让学生对运动过程有个全面的理解,学生就能找到相应的某一过程来分析,就可以找到相应的规律,问题就可以解决了.相反的,如果是匀减速直线运动,也可以用逆向思维,这样对培养学生的思维能力更有帮助.学生对于这种情况比较的熟悉,也很贴合身边发生的,学生掌握起来还是很容易的.
二、以角速度为切入点,分析物体的运动
圆周运动是高中物理中一个很重要的运动形式,相对于直线运动,属于学生比较难以理解和掌握的内容,学生也比较难以找到其中的规律,在常年的教学中,我以角速度为切入点,通过分析角速度这个物理量的变化,分析清楚物理的运动情况,从物体的运动状态变化而找到问题的解决方法.

图1
例2如图1所示,两个质量均为m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为L,b与转轴的距离为2L.木块与圆盘的最大静摩擦力为木块所受重力的k倍,重力加速度大小为g,若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度.下列说法正确的是( ).
A.b一定比a先开始滑动

C.a、b所受的摩擦力始终相等
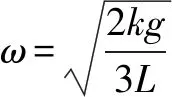
这道题学生做起来普遍觉得比较难,主要原因是学生不知道从何下手.我们老师在引导学生分析的时候可以以角速度ω为切入点.比如,当角速度ω从小逐渐变大的过程中,物体的运动出现什么样的变化,我们把每一个角速度ω物体所对应的状态想清楚,并罗列出来,学生对过程的发展就有一个全面的认识.又因为每一时刻a、b两物体均可视为做匀速圆周运动,所以物体的所需的向心力完全由其所受的静摩擦力来提供,即Ff=mω2r,而静摩檫力是有最大值的,所以当静摩檫力达到最大值时,ω也达到最大值,即临界状态就出现了.这样,学生找到了问题解决的切入点,又抓住了分析物体的运动过程的一条主线——角速度的变化,解题就容易多了.
三、以速度的变化为突破点,分析物体的运动
带电粒子在磁场中的运动是每年高考的必考的热门考点,也是同学们最为头疼的一个知识点,因为这个知识点虽然不多,但是关系复杂,而且题型千变万化,让人捉摸不透.但我们如果在指导学生的时候,在其他物理量不变的前提下,速度与半径就成为一一对应的关系,这样如果以速度的变化为突破口,学生就找到了解题的钥匙.
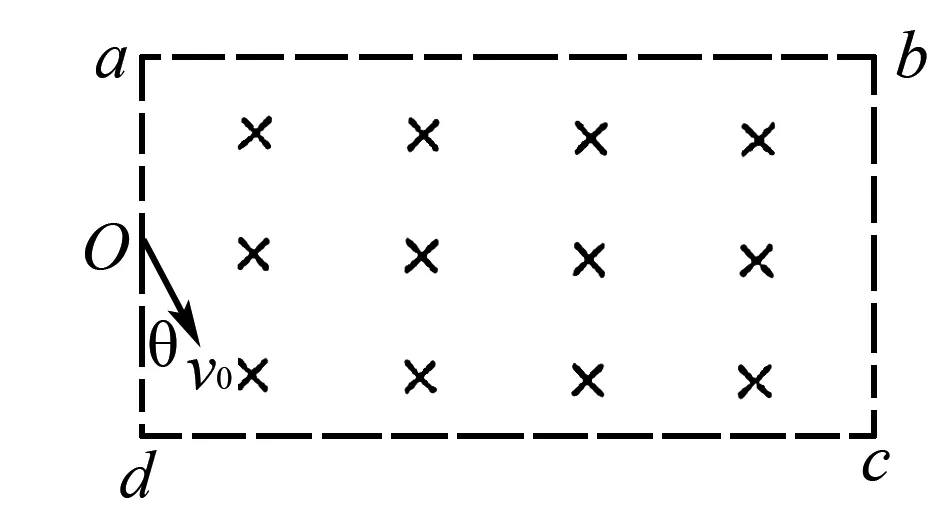
图2
例3如图2所示,一足够长的矩形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场,在ad边中点O,方向垂直磁场向里射入一速度方向跟ad边夹角θ=30°、大小为v0(未知量)的带正电粒子,己知粒子质量为m,电量为q,ad边长为L,ab边足够长,粒子重力不计,求:
(1)若粒子恰好不能从磁场下边界射出,求粒子的入射速度大小V01;
(2)若粒子恰好沿磁场上边界切线射出,求粒子的入射速度大小V02.
(3)若带电粒子的速度v0大小可取任意值,求粒子在磁场中运动的最长时间.
通过这样的分析,学生抓住了速度的变化这一关键量,利用所学知识分析清楚了物体运动轨迹的变化.在以速度与半径成正比的关系中,找到了轨迹与磁场边界相切这一临界状态.理解了临界状态的出现,学生才比较容易掌握其中的规律,找到解题的钥匙.通过这样的分析,找出自变量“速度”,从而找出因变量“半径”.既能让学生顺利解出题目所求,又能培养学生的分析、综合和推理能力.
四、以电流的变化为线索,分析物体的受力
在电学内容的教学中,我们常常遇到学生因为情景太抽象而无法理解的尴尬,电是看不见也摸不着的东西,学生也在从小就受旁人的警告中产生了对电的畏惧,这更加大了我们教学的难度.其实我们在电路电学的教学中,电流是电器设备工作的前提,电流对于电器设备,就像血液对于人一样的重要.而电流一旦变化,就会引起一系列参数的变化.所以抓住电流这条主线,利用电流与其他的物理量的关系,我们很多问题就可以迎刃而解了.
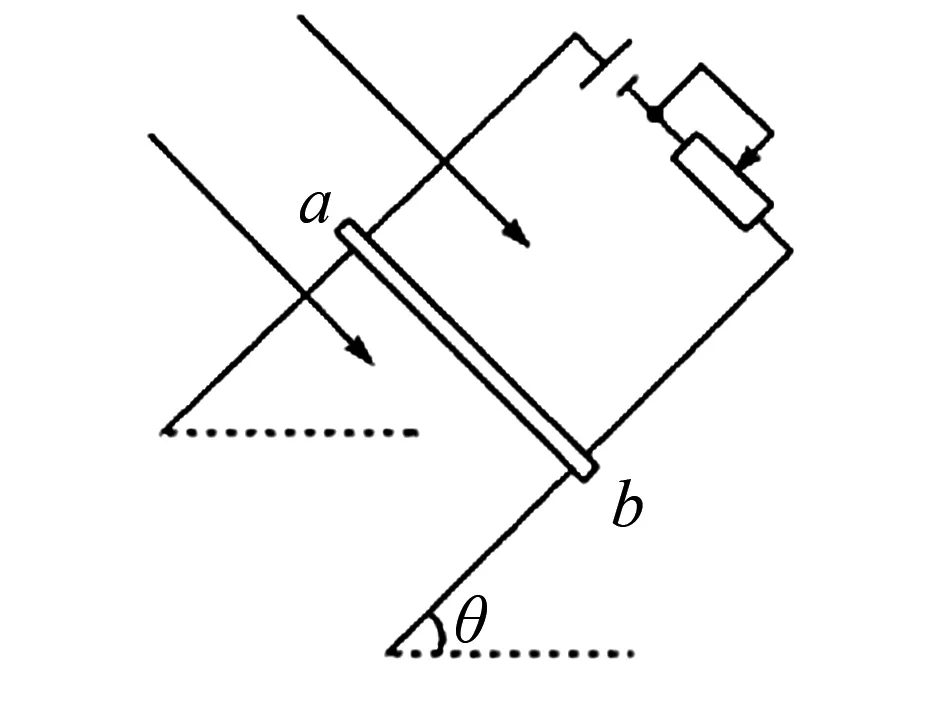
图3
例4质量m=0.02kg、长度L=0.3m的通电细杆ab置于倾角θ=37°的平行放置的导轨上,导轨的宽度d=0.2m,杆ab与导轨间的动摩擦因数μ=0.4,磁感应强度B=2T的匀强磁场与导轨平面垂直且方向向下,如图3所示.现调节滑动变阻器的滑片,试求:为使杆ab静止,通过杆ab的电流范围为多少?(g取10N/kg)
本题在解题中,学生在对杆ab受力分析上比较容易出错,学生习惯思维,就会认为因为杆ab所受摩擦力的方向向上,殊不知ab杆所受的静摩檫力沿斜面向下还是向上是不确定的,而与所受安培力的大小有关.如果老师引导学生以电流的变化为线索,当电流由零逐渐变大时,由安培力F=BIL知,在其他两个物理量不变的前提下,杆ab所受的安培力也从零开始逐渐变大,且由左手定则知,安培力的方向沿斜面向上.综合杆的平衡状态易知则ab所受的静摩檫力开始先沿斜面向上慢慢变小到零,然后在沿斜面向下慢慢增大到最大静摩檫力.有了电流这条主线,就找到了静摩檫力这个变化的物理量,学生在分析的过程中找到了物理量的因果关系,这样学生掌握起来就没有那么困难和抽象.
物理是一门以事实为依据,实验为基础的学科,每一件事情的发展都有相应的规律,其规律都有一个“自变量”这个“因”,我们只有能教会学生掌握找出“因”,就能找到相应的“果”,这对培养学生的唯物主义的世界观有着重要的帮助,为学生奠定良好的思维方式的基础,为学生的终身发展服务,达到立德树人的教育目标.
