黄河干流白银市水川段水面线计算方法对比分析

杨亮亮

(广晟昊兴勘测设计有限公司甘肃分公司，甘肃 兰州 730000)

黄河干流在甘肃境内全长913km，分别流经甘南、临夏、兰州、白银4个市(州)的9个县6个区。近年来，为完善白银市城市防洪体系，避免已建防洪堤带病运行，提升重要城市防洪减灾能力，对黄河干流白银段进行防洪治理。本次黄河干流白银段防洪治理工程中一个关键问题是确定各洪水频率工况下的河道水面线位置，为堤防和护岸工程的加高加固提供理论依据。采用能量方程逐段试算法(伯努利方程法)对白银市段局部区域内的水面线进行计算，但由于能量方程逐段试算法是一种一维方法，且在适用条件和计算方法上存在诸多的局限，使计算结果在可靠性方面还存在一定的问题。为对计算结果进行进一步的校核，本次水面线复核计算采用二维水动力数值模型，对多种洪水频率工况下黄河干流白银市水川段的水面线高程进行模拟计算，并对能量方程逐段试算法计算结果进行复核和评价。

1 能量方程逐段试算法

黄河干流上游白银段洪水相对涨落较缓，洪水历时和间隔较长，洪次较少，水面线推算时认为河段设计洪水下的水流流态是明渠恒定渐变流。在明渠恒定渐变流条件下，工程设计时选择一维能量方程来推求河道不同断面的水位[1]。天然河道水面线计算基本方程为

(1)

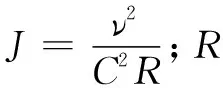
2 二维水动力数值分析

为克服能量逐段试算法在河道水面线计算上的局限和不足，本文对计算结果进行进一步的校核优化，采用二维水动力数值模型，对多种洪水频率工况下黄河干流白银市水川段水面线高程进行模拟计算，并与一维能量方程推求的河道水面线计算结果进行比较，对能量方程逐段试算法计算结果进行复核和评价。

2.1 计算方程

采用二维浅水方程来描述典型河段的水流流动问题，并选择Poisson方程作为坐标转换方程，把物理域上的不规则区域转化为计算域上矩形区域，因为不规则的边界在离散时可能会出现显著的误差[2-3]。曲线坐标系下的二维浅水方程包括：

a.沿水深积分的连续方程：

(1)

式中：u、v分别为ξ、η方向上的水流速度，m/s；Gξξ、Gηη分别为曲线坐标系转换成直角坐标的转换系数；d为基准水位下的水深，m；ζ为基准水位(z=0)以上的水位，m。

b.动量方程:

(2)

(3)

式中：u、v、Gξξ、Gηη含义同上；fu、fv分别为柯氏力系数(地理纬度北纬33°)，1/s；Fξ、Fη分别为ξ、η方向上的紊动动量通量，kg/s2。

c.定解条件：

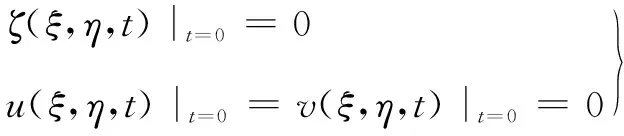
边界条件：出、入流边界上，给定水位、流速或流量过程，固壁边界采用无滑移边界条件。

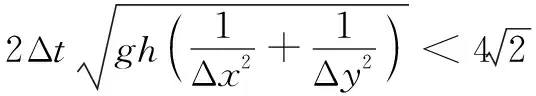
2.2 计算方法

本次模拟计算的数值离散方法采用有限差分法，计算方法是基于交错网格的交替方向显、隐式混合格式，即ADI法。ADI方法将一个时间步长分为两个时间层，各由半个时间步长组成。在每一时间层中，模型方程的所有项通过在空间上至少有二阶精度的相同方法求解。ADI方法的优点是计算稳定性好、计算精度高，缺点是灵活性差，不适用于具有混合偏导数的情况。在二维模拟计算中，ADI方法是无条件稳定的[4]。

3 工程实例

3.1 计算模型

3.1.1 断面布置

黄河干流在白银市境内流经白银区、靖远县、平川区、景泰县，自西南的大峡水电站库区流入，经白银区，至景泰县红柳后拐向西北，经过景泰县五佛后折向东北流出甘肃境内，辖区内河道弯曲，平面上大致呈“S”形，境内河长254km，主要为天然河道段。根据河道分段及断面布置原则，共划分244条横断面，平均断面间距500m。本次计算范围从横1断面至横37断面，河道长度约21km，计算范围内包含38个实测横断面，上游边界为大峡水电站；乌金峡水电站在计算区域下边界下游约9km处，其尾水影响范围至横23断面；安宁渡水文站位于计算范围下边界下游约70km处。图2为黄河干流白银市水川段计算区域示意图。

图2中蓝色线表示本次防洪治理工程设计状况计算范围，与天然状况下计算范围不同的地方用黄色线标示。由图2可知，天然状况和设计状况计算区域的主要差异位于横11断面至横30断面之间。

3.1.2 网格划分

由于天然状况和设计状况计算区域不同，在计算中须生成2套网格分别对天然条件下和设计条件下的工况进行计算。在本次模拟计算中所采用的天然状况和设计状况下的网格点数分别为29×761和22×756。白银市水川段天然状况和设计状况计算网格见图3。

图3 白银市水川段设计状况计算网格

3.1.3 地形插值

为在模拟计算中真实反映计算段河道的地理信息，采用地形插值方法对白银市水川段计算区域内的高程散点进行插值计算生成地形文件[5]。插值计算所涉及的高程散点总数为1403370个，其中横断面散点数为2514个，等高线散点数为1393638个，地形高程散点数为7218个。白银市水川段插值地形图见图4。

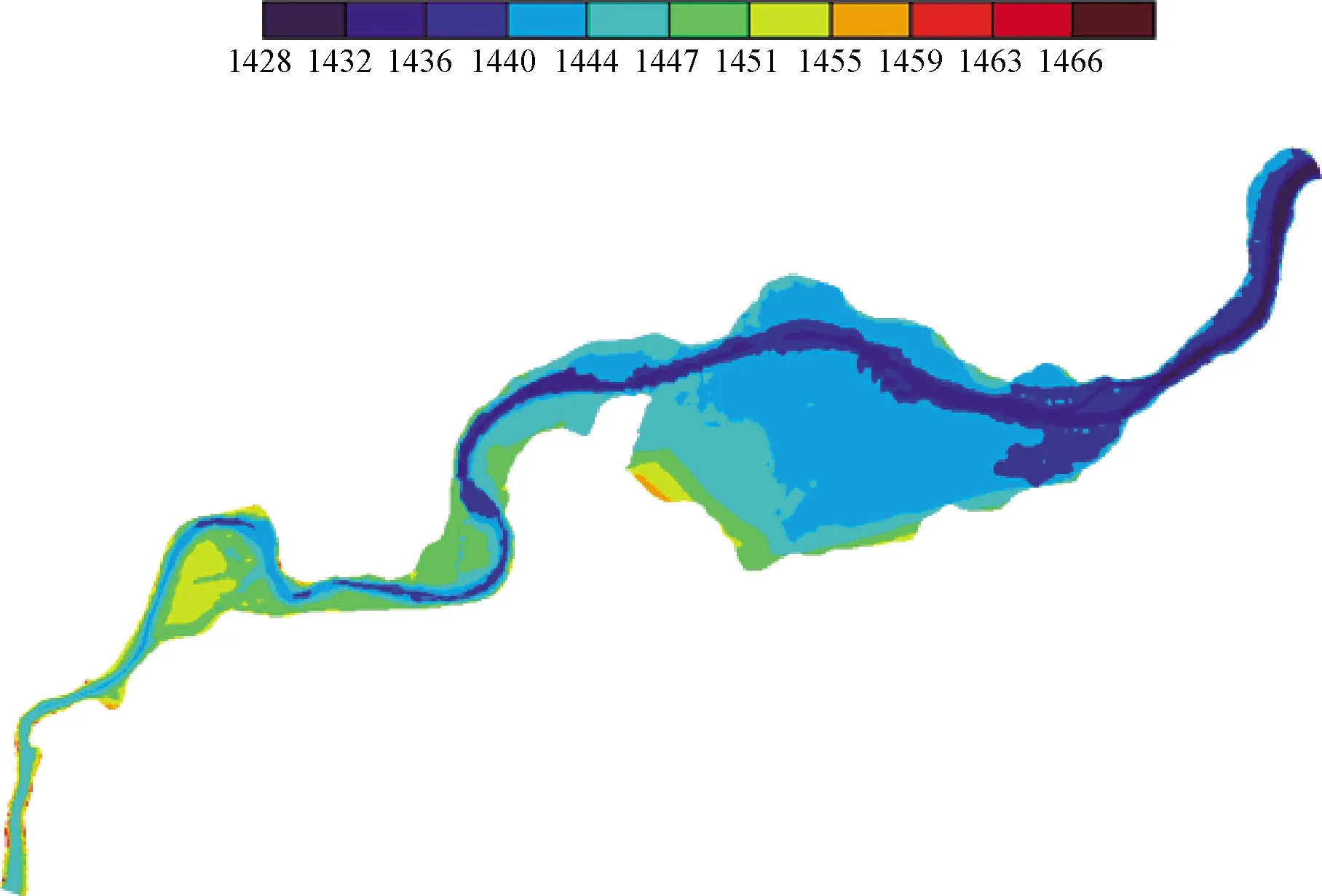
图4 白银市水川段天然状况插值地形图

3.2 计算工况

白银市水川段计算分10年一遇洪水、2012年实测最大洪水、5年一遇枯水期施工洪水和冬季实测流量4种工况，具体计算工况见表1。

表1 白银市水川段计算工况

边界条件：两种方法在河道水面线计算时，工况4的下游水位边界条件采用实测值。对于工况1～工况3，由于缺乏水位实测资料，采用能量方程计算值作为下游边界条件。

3.3 糙率取值

由白银市安宁渡水文站实测糙率-流量关系(见图5)可知，糙率实测值在流量为1000m3/s上下时有明显区别：当流量大于1000m3/s时，糙率值变化不大，介于0.025～0.032之间；当流量小于1000m3/s时，糙率值随流量减小而显著增大，介于0.030～0.060之间。因此，在本次模拟计算中，对工况1～工况3(Q>1000m3/s)，采用同一套槽-滩-植被的率定糙率组合值，对工况4(Q=600m3/s)，由于流量小，水流不上滩，因此在计算区域内不设边滩、植被糙率，取安宁渡水文站实测糙率值0.045(可由图5得到)。在对工况1～工况3的模拟计算中进行比选的糙率组合有：ⓐ河道主槽糙率0.03，边滩糙率0.05，植被糙率0.06～0.15；ⓑ河道主槽糙率0.03，边滩和植被糙率0.04；ⓒ河道主槽糙率0.03，边滩和植被糙率0.06；ⓓ河道主槽糙率0.03，边滩糙率0.05，植被糙率0.10。

采用上述糙率组合对白银市水川段工况进行模拟计算，将其计算结果与能量方程计算值进行比较，选择拟合结果最优的第一组糙率组合为工况1～工况3模拟计算的糙率组合值，糙率值的具体分布见图5(天然状况下)。

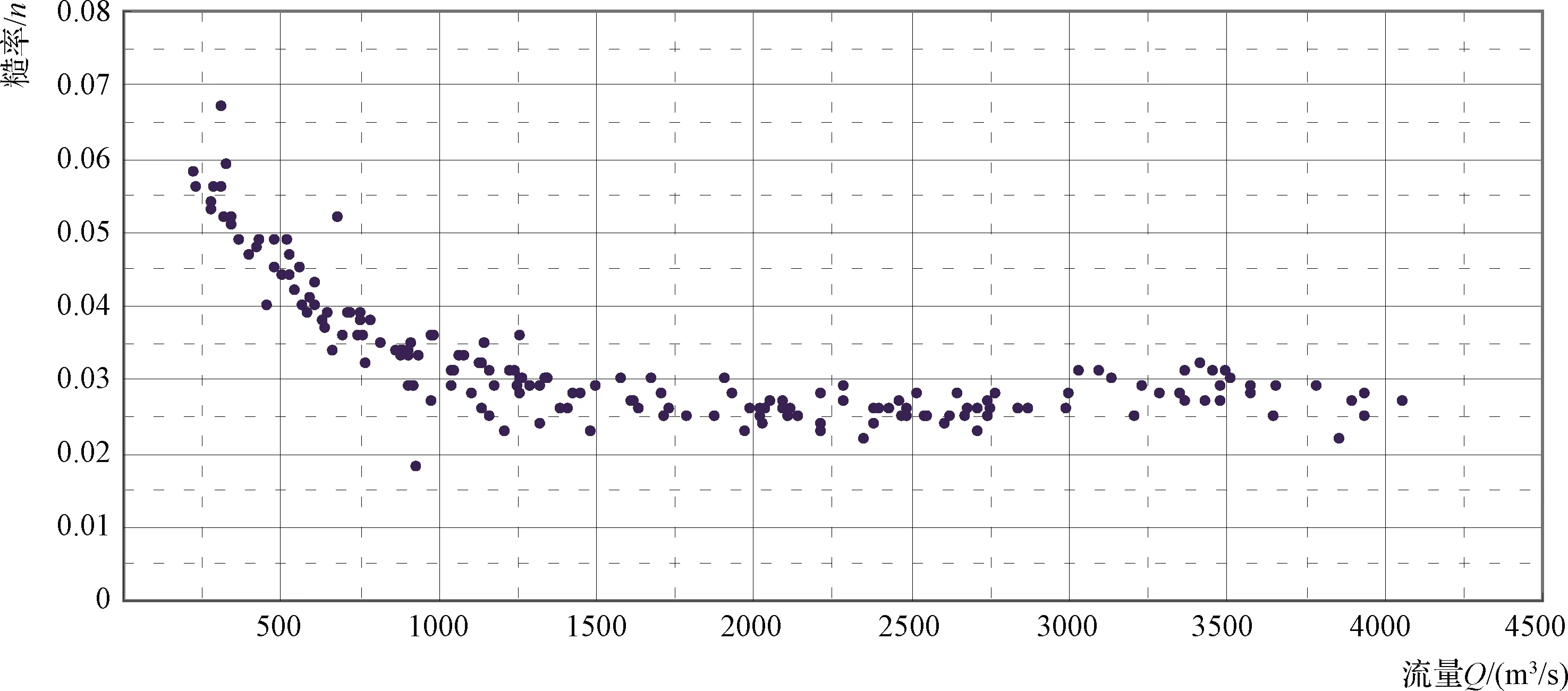
图5 安宁渡水文站实测糙率-流量关系散点图

3.4 模型合理性验证

2012年12月1—3日对白银市水川段进行了水位流量现场观测(工况4)。利用该实测资料对模型进行率定，由于冬季流量较小，水流不上滩，因此在整个计算范围内采用单一糙率值0.045。白银市水川段沿程各断面上的实测值、二维计算结果和两者之间的差值见表2。工况4的二维计算值与实测值的对比见图6。由于横23断面后的区域内水位受下游乌金峡水电站尾水影响，其尾水影响无法在二维数值模型中进行模拟，因此本文仅比较分析横1断面至横23断面间区域的结果。由表2可知，二维计算结果与实测值之间的最大差值为1.50m，出现在横19断面。

由图6可知，二维计算值与实测值之间差值主要出现在横3断面至横8断面、横15断面至横17断面以及横19断面至横22断面。具体原因分析如下：

a.由图6可知，二维计算值在横3断面至横8断面间低于实测值，其主要原因是二维计算值在横2断面和横3断面间存在突降现象。由横2断面至横4断面的地形图和实地踏勘可知：横2断面至横3断面之间距离较大(约1.4km)，远大于水川段的平均横断面距离(500m)，水流在横2断面以后先经过一个近90°的弯道，且伴随有明显的河床缩窄现象。天然工况1条件下横1断面至横3断面流速分布见图7，由图7可知，水流在出弯以后呈现向对岸折冲的趋势，主流整体偏向右岸，左岸局部出现小范围回流，经过一段距离的调整，主流在横3断面处回到河道中心。理论上，以上地形与河势条件会引起河道内水流的能量损耗，使横2断面上游局部出现壅水，横2断面和横3断面间出现较明显的水位跌落现象。本次模拟计算中进行了多组针对糙率与地形的数值试验，结果表明横2断面与横3断面间较大的水位跌落不可避免。由于横2断面至横3断面间较大的水位跌落现象，造成了平面二维计算水位值在横3断面至横8断面间整体低于实测值。

b.二维计算值在横15断面至横17断面间低于实测值，其原因也与横14断面至横17断面之间的地形和河势有关。该河段为45°弯道，且在横15断面存在河心洲，受河心洲的挤压，横15断面附近水面宽度仅为横14断面水面宽度的一半。受地形和河势的影响，二维计算值在横14断面和横15断面间出现跌落现象。同样，在横17断面下游约50m处，河道中再次出现阻水洲滩，使过水断面再次缩窄，水面宽度约为横17断面处水面宽度的3/5左右，且河床底高程出现负坡，造成横16断面至横17断面水面坡降放缓。

c.二维模拟值在横19断面至横22断面间高于实测值。结合实测地形可知：一方面，横18断面至横20断面间，以及横25断面至横27断面间河道中央各有一个洲，在横20断面和横24断面，河道有两处明显束窄；另一方面，横18断面至横19断面河床为负坡，横19断面至横24断面，河床坡度较缓。综合两方面因素，造成横19断面至横22断面的壅水现象，水面坡降放缓。

4 计算结果分析

由于横23断面后的区域内水位受下游乌金峡水电站尾水影响，其尾水影响无法在二维数值模型中进行模拟，本文仅分析各工况下横1断面至横23断面间区域的计算结果。篇幅所限，10年一遇洪水(天然状况计算结果)见表3，列出两个工况(工况2和工况3)下能量方程逐段试算法与二维数值计算值进行比较分析，比较结果见表4，二维计算值与能量方程计算值的对比见图8。

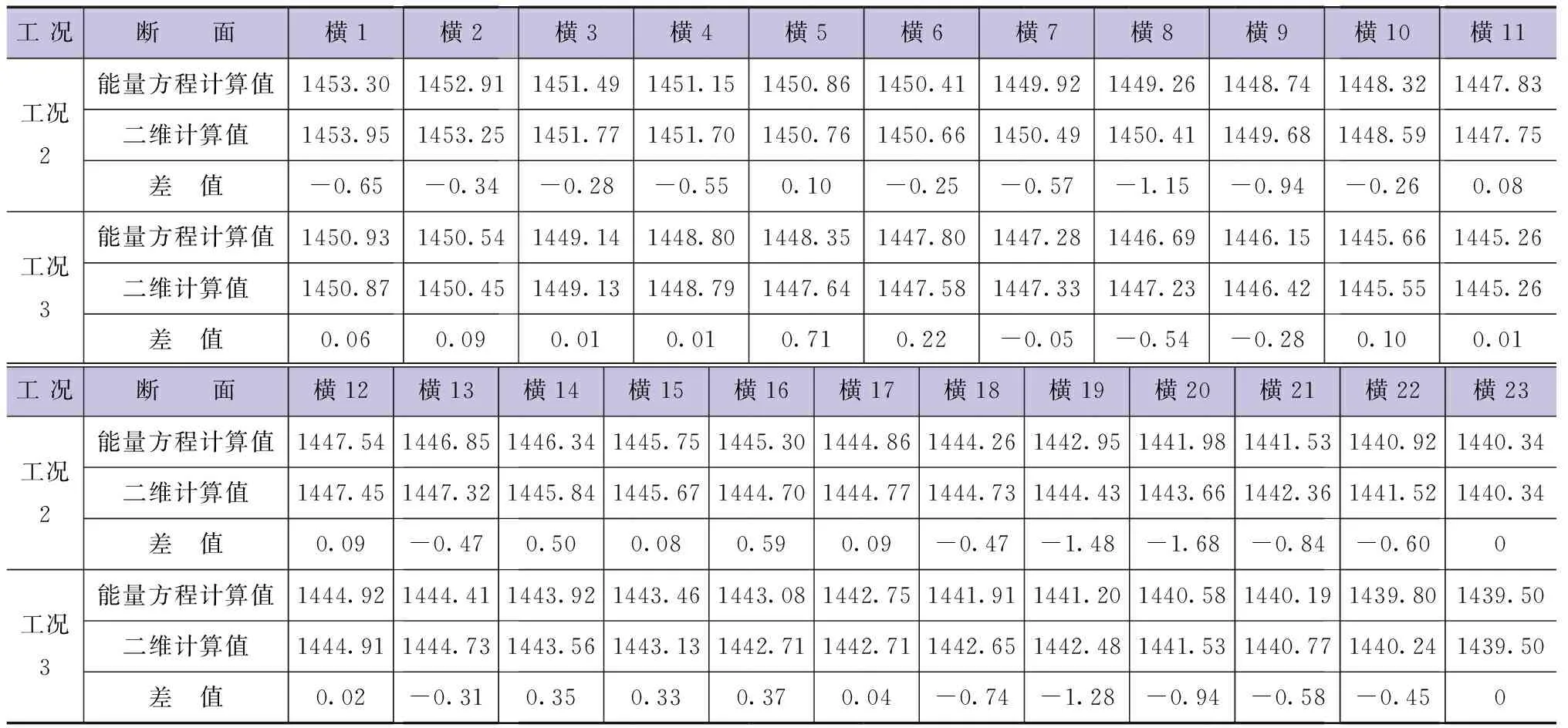
表4 二维计算水位高程与能量方程计算值比较成果(工况2和工况3) 单位：m

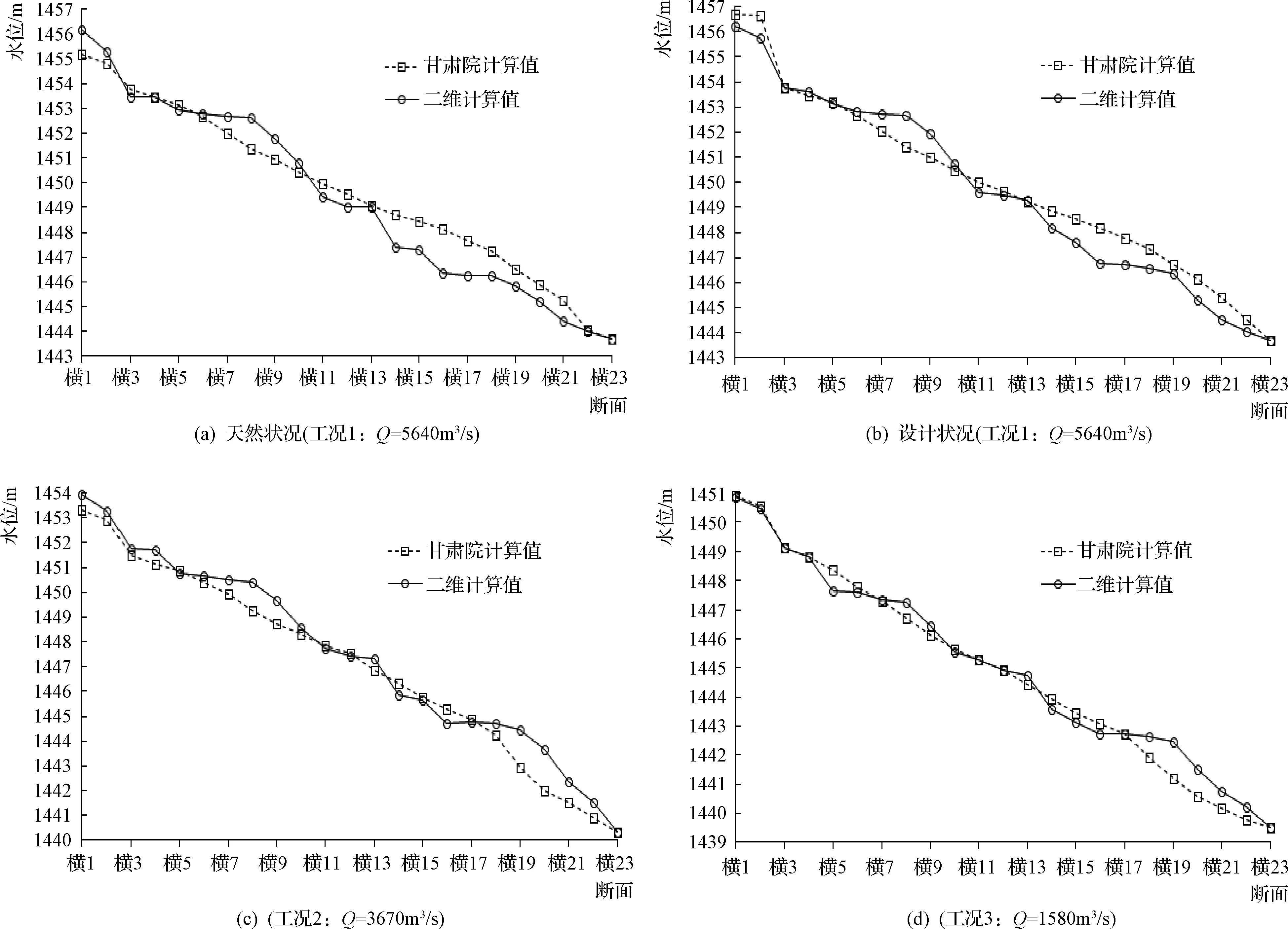
图8 白银市水川段水面线沿程分布

由两种计算方法比较可知：在下游边界取能量方程逐段试算法计算值的情况下，对于工况1的天然状况和设计状况，二维计算值与能量方程计算值的最大差值分别为1.77m和1.44m，均出现在横16断面；对于工况2、工况3和工况4，二维计算值与能量方程计算值的最大差值分别为1.68m、1.28m和1.20m，分别出现在横20断面、横19断面和横19断面。

由图8可知：

a.二维计算值与能量方程计算值的最大差值为1.77m，发生在天然工况1的横16断面。

b.在大流量工况(工况1和工况2)下，横6断面至横10断面间的二维计算值大于能量方程计算值，且在该河段以较大比降下降；随着流量降低，横6断面至横10断面间二维计算值开始减小，部分或全部低于能量方程计算值，但仍维持较大比降。这是因为横6断面至横10断面间河道有两个大角度的转角，且伴随有河床束窄的现象。随着河道中水位降低，地形的影响开始占据主导地位。

c.工况1的天然状况和设计状况下，二维计算值在横13断面至横23断面间均低于能量方程计算值，这是由于横13断面至横16断面间的水面线较大幅度的降落引起的。横12断面至横16断面间为一个近120°的弯道，弯道内侧为顾家善，是一块滩地。在10年一遇洪水工况下，水流上滩，使横12断面至横16断面间的糙率增加，再加上弯道的作用，使横13断面至横16断面间的水面线产生突降。一维模型中采用综合糙率，难以考虑水流上滩所引起的糙率增大现象和弯道的影响，可能致使二维计算值在横13断面至横23断面间低于能量方程计算值。随着流量的降低，工况2～工况4中顾家善区域内均无水流上滩现象，因此在二维计算中没有造成糙率的突然增大，因此对比能量方程计算值，没有出现水面线的突降。随着河道中水位的降低，地形的影响开始占据主导地位，横19断面至横22断面间的壅水现象开始控制横18断面至横23断面的水位值，使这段河道中的二维计算值大于能量方程计算值。

5 结论及建议

利用能量方程和二维水动力数值模型，在10年一遇洪水、2012年实测最大洪水、5年一遇枯水期施工洪水和冬季实测流量4种工况下对黄河干流白银市水川段水面线高程进行计算，并对两种计算结果进行比较分析，得到以下结论：

a.一维能量方程是计算河道水面线的基本理论与方法，是一种适用于恒定流的方法，适用于河道顺直、河道平面形态变化不大且两推算断面间过水断面相对均匀的河段，能量方程逐段试算法基本满足防洪工程一般河道水面线的需要，是一种适用广泛、简便易行的工程计算分析方法。

b.二维浅水方程适用于研究海岸、河道入海口、湖泊、大型水库等具有广阔水域的地区，对河道弯道、断面突变、河道水位突降、壅水以及糙率系数变化的河段计算结果准确，当用于河流水面线计算时，适合于研究具有大片滩地的河段。在洪水到来时，如整个滩地上的水流不能假定是沿同一方向的，则应建立二维模型，充分地重演洪水的侧向演进。

总之，工程设计中可将一维、二维模型嵌套计算，建议对于相对顺直，有堤防约束的河段，可用能量方程计算河道水面线；对于局部地形复杂，水流在滩、槽之间游移变动的河段，以及存在大片滩地的天然状况或者无堤防约束的洪水漫流等，可利用二维浅水方程进行建模计算。同时两种计算方法在河道沿线堤防进行提前预报、预警方面有重要的意义，针对预警结果采取相应的应急措施，能够快速准确地进行防洪。