延期时差对多截面承重立柱框架结构拆除爆破效果的影响❋
2021-04-14高文乐赵德龙李元振张泽华李坤鹏
高文乐 赵德龙 李元振 张泽华 李坤鹏
①山东科技大学土木工程与建筑学院(山东青岛,266590)
②中国石油大学(华东)储运与建筑工程学院(山东青岛,266580)
引言
伴随着我国城市化进程的加快,城市楼房改造和拆除重建的工程越来越多。 爆破拆除因其具有安全高效、经济环保等优点而占有重要地位。 爆破拆除理论的发展落后于实践,目前爆破拆除方案的设计仍以经验公式为主;但拆除对象的结构及其所处的环境日趋复杂,各方面对爆破拆除的要求也越来越高。 因此,爆破拆除必须向精确化、可控化方向发展。 爆破拆除具有不可逆性,对其进行实体实验较为困难;因此,有必要通过数值模拟的方式对爆破方案的制定和参数的优化设计提供参考依据。
在拆除爆破中,延期时差的不同会直接影响爆破振动的强弱、飞石范围的大小以及建(构)筑物倒塌效果的好坏[1]。 王涛等[2]采用了数值模拟来预测建筑物倒塌并得到了较好的效果,提出切口部位施加爆炸载荷能更真实地模拟建筑物爆破拆除倒塌过程;张明等[3]利用ANSYS/LS-DYNA 有限元分析软件,采用整体式模型研究得出:在相同切口形式时,爆破区段延期时间不同,框架结构塑性铰形成位置和倒塌效果有所不同;李胜林等[4]采用内爆法,对单榀钢混框架进行不同延期时间的爆破切口的数值模拟,并提出了延期时间的确定原则;田水龙等[5]研究了不同毫秒延时对后坐的影响;徐鹏飞[6]采用有限元分析方法对混凝土材料模型以及钢筋混凝土本构模型进行了研究。 本文中,以多截面承重立柱酒店爆破拆除项目为例,利用ANSYS/LS-DYNA 软件建立有限元模型,进行数值模拟,探究延期时差对拆除爆破效果的影响;通过现场实际爆破倒塌情况和模拟情况对比,分析有限元模拟的实际工程价值,为类似的工程提供参考借鉴。
1 工程概况
1.1 爆破环境
待拆除酒店位于山东省烟台市开发区长江路与珠江路交叉口西南侧。 因所在地块重新规划建设,地块内建筑物需要被拆除。 该酒店北侧75 m 为长江路;东侧133 m 为珠江路;南侧50 m 为需要保留的平房,88 m 为待拆除楼房;西侧距离二层锅炉房15 m,距离办公楼30 m。 爆破环境示意图见图1。
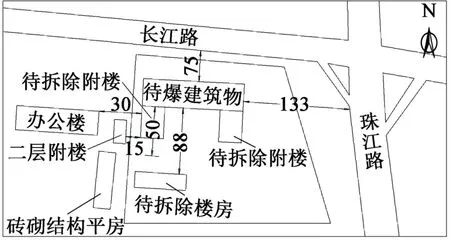
图1 爆破环境(单位:m)Fig.1 Blasting environment(unit:m)
1.2 结构特点
该酒店主体结构8 层(局部10 层),框架结构。高36.4 m,东西长95.3 m,南北宽17.3 m,建筑面积13 000 m2。 建筑物主体结构东西方向共16 排立柱,跨度为3.9 ~9.0 m;南北方向3 排立柱,跨度为2.2 ~8.6 m;单层共计48 根承重框架立柱。 框架柱的截面尺寸有700 mm×700 mm、850 mm×850 mm、1 400 mm×675 mm 3 种类型,纵向配筋情况分别为16φ20、24φ20、24φ22。 建筑物立柱布置见图2。

图2 建筑物立柱布置图(单位:mm)Fig.2 Layout of building columns (unit:mm)
2 爆破方案
考虑被爆建筑物的结构特点和周边环境情况,决定采用向南定向倒塌的爆破方案。 由于该建筑物楼层较高、结构稳定,决定采用三角形爆破切口,切口的上仰角为30°。 将第1 ~3 层设为爆破切口,缺口高度南高北低(第1 层切口最大高度3.9 m、第2层切口最大高度3.6 m、第3 层切口最大高度3.0 m),爆破切口最高处为10.5 m。 爆破切口示意图见图3。

图3 爆破切口(单位:m)Fig.3 Blasting incision(unit:m)
爆破后,建筑物的支撑稳定性被破坏,在自身重力作用下向南定向倒塌。 根据倒塌方向,采用自南向北逐排逐层延期起爆方式。 为了快速形成爆破切口,加快建筑物向南侧倾斜的速度,自南向北各排立柱分别采用非电毫秒延期雷管MS3 段、MS11 段和MS15 段,延期时间分别为 50、460 ms 和 880 ms。
3 不同延期时差下的数值模拟
3.1 有限元模型建立
利用ANSYS/LS-DYNA 有限元软件对工程进行1︰1 建模[7]。 为了能够真实地反映出钢筋和混凝土两种材料的力学性能差异,采用分离式共节点模型。 其中,梁、柱和地面选用solid 164 单元,钢筋选用beam 161 单元,楼板选用shell 163 单元。 为了提高建模和计算的速度,在不严重影响计算精度的前提下,对模型做出了以下简化[8]:1)不考虑钢筋外面的混凝土保护层厚度;2)不设置箍筋,通过适当提高混凝土强度来代替箍筋的作用;3)地面设置为刚体,不发生变形;4)将墙的质量等效分配到梁上;5)不考虑炸药爆炸对切口的形成以及爆炸后切口断面的影响。 同时,考虑到计算的准确性,采用规则的六面体映射网格进行网格划分,网格尺寸设置为0.2 m,单元数量总计344 703 个。 结构的有限元模型见图4。

图4 结构的有限元模型Fig.4 Finite element model of structure
3.2 模型的材料及接触
钢筋和混凝土的材料类型选用∗Mat_Plastic_Kinematic(塑性随动模型),各材料的力学性能参数如表1 所示。 通过关键字∗Mat_Add_Erosion 控制爆破切口的形成以及混凝土材料的失效[9],钢筋的失效则通过定义材料自带的FS 参数进行控制。
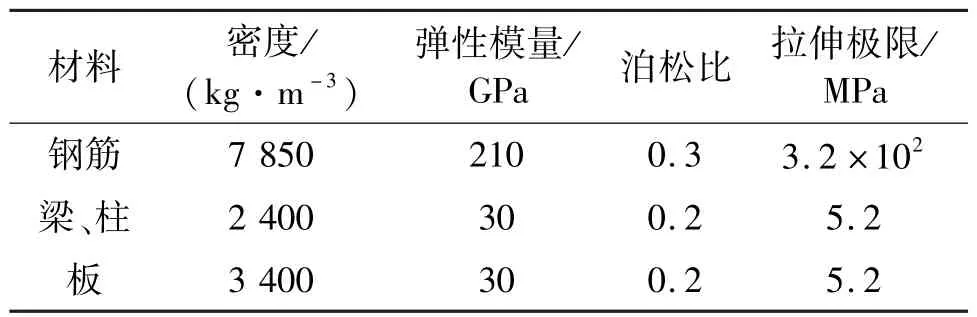
表1 各材料的力学性能参数Tab.1 Mechanical property parameters of each material
考虑到建(构)筑物在倒塌过程中接触的复杂性,在各种接触类型中,用Contact_Eroding_Single_Surface 定义混凝土单元之间以及混凝土单元和地面的接触;用Contact_Nodes_To_Surface 定义钢筋单元和地面的接触[10],防止钢筋穿透地面。 模拟时,取静摩擦系数和动摩擦系数为0.6。
3.3 不同延期时差设置
有限元模型建立完毕后,设置8 种不同的延期方案,延期时差分别为 0、100、200、300、400、500、600 ms 和 900 ms。 其中,8 种延期方案相邻两排立柱之间的延期时差相同。 通过ANSYS/LS-DYNA 进行模拟,分析不同延期时差下多截面承重立柱框架结构的拆除爆破效果。
4 数值模拟结果及对比分析
4.1 数值模拟结果
模型的其他设置保持不变,只改变延期时差,通过数值模拟得到各个延期方案的爆破效果。 不同时差时的最终倒塌效果见图5。 利用LS-DYNA 的后处理模块对图5 中不同延期时差时的倒塌形态进行数据处理,得到不同延期方案的爆堆高度(图6)及后坐距离(图7)。
4.2 对比分析

图5 不同延期时差的倒塌效果示意图Fig.5 Schematic diagram of collapse outcome with different delay time difference

图6 不同延期时差时的爆堆高度Fig.6 Blasting height with different delay time difference

图7 不同延期时差下的后坐距离Fig.7 Rear-seat distance with different delay time difference
通过对徐轩等[11]的研究和本次数值模拟结果的相互论证可以发现,控制延期时差的大小可以有效地将爆堆高度和后坐距离控制在可承受的范围内,降低爆破拆除产生的不良影响。
4.2.1 爆堆高度
以爆堆的最高点作为爆堆高度的选取点。 从图5 和图6 中可以看出,爆堆高度随着延期时差的增加呈先减后增、最后趋于稳定的变化规律,并在500 ms 出现最小值。 其中,延期时差为100 ms 时,由于东北侧一根立柱尺寸为1 400 mm×675 mm,南北向截面刚度较大,在倒塌过程中立柱未完全破碎并且翘起,导致爆堆高度在延期时差100 ms 时陡升。 结构的破碎解体主要依靠构件之间的冲击碰撞作用,当延期时差较小时,在大偏心受压下,最后一排形成塑性铰,上部结构整体发生偏转,但仅第一排的动能会因为距塑性铰较远而比较大,无法使结构完全解体;随着延期时差的增大,每排立柱在梁柱节点处均能形成塑性铰,且在500 ms 时各塑性铰转动充分,产生的竖向动能足以使结构完全解体,爆堆高度为6.92 m;延期时差大于500 ms 后,塑性铰转动充分后并趋于稳定,部分动能转化为内能,能量的耗损反而不利于结构的解体,因此,爆堆高度趋于常数。
4.2.2 后坐距离
从图5 和图7 的数值模拟结果对比中可以发现,后坐距离随着延期时差的增加呈先减小后增大、最后趋于稳定的变化规律,并在400 ms 出现最小值。 楼体在爆破时会产生下坐和沿设计方向的倾倒[12]。 延期时差较小,塑性铰集中在最后一排立柱处;当爆破切口形成后,最后一排立柱承受剩余悬臂结构的全部重力和弯矩,塑性铰迅速破坏;当爆破切口闭合时,水平向动能依据作用力与反作用力原理,会使楼体在相反方向产生后坐,导致结构发生较大后坐。 随着延期时差的增大,各排立柱相继形成塑性铰,并且在延期时差为400 ms 时塑性铰充分转动,动能转化为内能,后坐距离达到最小,为7. 47 m。 随着延期时差的继续增大,前端结构提前触地,对后端结构产生支撑作用,导致后坐增大,最终稳定在一个常数。
5 现场爆破效果
综合考虑最小爆堆高度以及最小后坐距离的原则,爆破方案最终选取自南向北排间延期时差分别为410 ms 和420 ms。 具体通过非电毫秒延期雷管实现。 现场爆破过程如图8 所示,

图8 爆破倒塌过程Fig.8 Collapse process of blasting
起爆后,结构按预定方向倒塌。 对实际爆破和数值模拟的爆堆形态进行对比:实际爆堆高度约8.10 m,后坐距离约6.20 m;数值模拟的爆堆高度为7.36 m,后坐距离为6.81 m。 可认为现场爆破效果与模拟结果比较符合,模拟结果较好。
本次爆破中,整体产生了明显的后坐现象。 分析其主要原因为结构的高宽比仅为1.77,楼房重心偏低,导致支撑体受到偏心力超过其最大的承载能力;支撑体因承载能力不足而迅速发生粉碎性破坏或弯折断裂破坏,楼体以一定角度下沉;同时,转动轴后移,即上部楼体开始做类似于自由落体运动与绕转动轴转动的合成运动[13]。 因此,在爆破施工时应合理地控制后排立柱的装药量,减少小高宽比结构因支撑体承载力不足而产生的后坐现象。
6 结论
1)通过与其他研究对比发现,框架结构在进行定向爆破拆除时,爆堆高度和后坐距离随着延期时差的增大先减小、后增加,最后趋于稳定。 最佳延期时差则根据不同的建筑形态有不同的数值。
2)为避免数值模拟中出现的大截面立柱破而不碎的情况,多截面承重立柱框架结构在爆破拆除时,应对截面刚度较大的立柱进行松动爆破,确保其完全解体。
3)模拟过程中建立的是分离式共节点模型,综合地考虑了钢筋和混凝土的共同作用,虽然没有考虑炸药在爆炸时对整体结构的冲击作用,但也能很好地模拟出结果,与实际工程吻合。
4)对于本文中的建筑形式,当爆堆高度最小时,数值模拟得到的最佳延期时差为500 ms;当后坐距离最小时,数值模拟得到的最佳延期时差为400 ms。 模拟结果也与实际爆破相符,说明数值模拟可以有效地对实际爆破结果进行模拟预测。
