基于混沌理论和GOA-K-means算法的有载分接开关状态特征分析计算方法
2021-04-13马宏忠
马宏忠 严 岩
基于混沌理论和GOA-K-means算法的有载分接开关状态特征分析计算方法
马宏忠 严 岩
(河海大学能源与电气学院 南京 211100)
为更加准确有效地监测变压器有载分接开关(OLTC)机械状态,针对传统基于K-means的监测方法聚类效果易受其初始聚类中心选择的影响,该文提出一种基于蝗虫算法(GOA)和K-means相结合的OLTC机械状态监测方法。首先针对OLTC振动信号的非线性和混沌特性,利用P-G法和互信息值法计算嵌入维数和延迟时间,对实测的OLTC振动信号进行相空间重构;其次应用Kolmogorov熵对重构后的振动信号混沌特性进行判断;最后为提高聚类精度,针对K-means对初始聚类中心的敏感性,将蝗虫算法引入该算法对其聚类中心进行优化,对重构后的高维振动信号采用优化的K-means聚类方法进行分析。研究结果表明:在OLTC的振动信号识别应用中,优化的K-means聚类算法得到的特征量计算结果具备一定的规律性。研究结果为OLTC的机械运行状态监测提供了一种新的途径。
蝗虫算法 有载分接开关 优化K-means 振动信号
0 引言
有载分接开关(On-Load Tap Changer, OLTC)是变压器的主要部件,也是变压器唯一的可动部件。OLTC的正确运行条件对高压直流输电系统的安全稳定至关重要,同时由于它也承受着电气和机械应力,因此使得OLTC成为变压器最脆弱的部件之一。依据国内外对有载调压故障的调查和统计资料显示:OLTC的故障率占变压器的整体故障率的20%以上,且触头和驱动机构等部件造成的机械故障占OLTC总故障的95%以上[1-3]。因此,研究有载调压变压器的分接开关机械故障诊断技术,对于维护变压器稳定运行具有重要意义。
目前,已有诸多学者对OLTC机械状态监测做了大量的理论和实践研究,主要方法包括:OLTC油中溶解气体分析[4]、电机驱动力矩分析[5]、温度分析[5]和振动信号监测技术[6-11],其中振动信号监测方法是目前主流的诊断方法。该方法最先是由ABB公司的C. Bengtsson等在1996年提出[8],其核心思想是借助加速度传感器对OLTC不同工况下的切换过程中的振动信号进行采集,从而实现对OLTC故障诊断。其中如何从采集到的振动信号中获取有效特征量来提高诊断结果精度是一个难点,已有国内外研究者对此进行了一些相关研究。例如,文献[9] E. Rivas等利用小波变换对振动信号进行分解,对振动信号的时域特征进行提取,利用自组织映射和遗传算法,将提取出的故障特征与正常的特征进行对比,建立OLTC的状态判断准则。文献[10]李庆民等利用OLTC振动信号与语音信号的相似性,将隐马尔可夫模型引入OLTC故障中,建立了OLTC的机械故障诊断策略。然而OLTC切换时获取的振动信号是随机、非平稳信号,传统的时频分析法不能从振动信号中获取较为丰富的诊断信息。文献[11]张先知等利用互补经验模态分解(Complementary Ensemble Empirical Mode Decomposition, CEEMD),提出基于固有模态函数(Intrinsic Mode Function, IMF)的段能量降噪算法,并设计出时频矩阵划分算法,对峭度、包络谱线等特征参数进行提取,但由于CEEMD分解算法在处理OLTC振动信号这类非线性瞬态数据时仍然会出现模态混叠等问题,从而导致分解结果及判据的有效性需进一步提高。文献[12]赵彤等基于OLTC的振动信号混沌特性,将一维振动信号利用相空间重构法在高维空间进行重构,并通过定义相点空间分布系数(Phase Point Distribution Coefficient, PPDC),对OLTC的不同工况进行识别,但由于忽略了重构信号的矢量特性,使得定义的评价指标对故障识别有限。文献[13]周翔等基于上述缺陷,通过K-means聚类法对重构后的实测OLTC振动信号进行聚类分析,并将聚类中心作为特征量对OLTC故障进行识别。但是由于K-means算法本身的缺陷,使得计算结果不具备规律性,从而导致OLTC振动信号的诊断结果不精确或者出现误判等情况。
针对上述算法的缺陷,本文提出了一种基于蝗虫算法(Grasshopper Optimization Algorithm, GOA)的K-means的初始聚类中心改进方法(GOA- Kmeans)。蝗虫优化算法是一种仿生优化算法,该算法具有计算简单、收敛速度快、精度高等优点[14]。函数优化测试表明[14]:蝗虫算法(GOA)与萤火虫算法(Firefly Alogrithm, FA)、粒子群算法(Particle Swarm Optimization, PSO)、差分进化算法(Differential Evolution Algorithm, DE)、万有引力算法(Gravitational Search Algorithm, GSA)、遗传算法(Genetic Algorithm, GA)、蝙蝠算法(Bat Algorithm, BA)、花授粉算法(Flower Pollination Algorithm, FPA)相比更具竞争力。该算法目前被应用于参数优化、特征选择及振动故障识别等方面[15-20],但目前尚未发现蝗虫改进聚类算法在OTLC机械故障诊断中的应用。因此本文采用蝗虫算法对K-means算法的初始聚类中心进行优化,并将改进的算法应用于OLTC实测振动数据进行验证。研究内容主要分为以下三部分:①针对OLTC的振动信号具有混沌特性,采用相空间重构算法对振动信号进行计算,并进行混沌特征判断;②基于传统K-means算法对初始聚类算法具有一定的敏感性,采用GOA算法对K-means算法进行改进;③针对传统K-means算法在判断OLTC故障时,得到的特征量不具备规律性的问题,将处理后的振动信号作为GOA-K-means算法的输入,进行计算得到特征量,将所得特征量与传统K-means算法得到的特征量进行对比验证。
1 OLTC振动信号重构
相空间重构理论最先是由J. D. Farmer提出的,并应用于研究时间序列的分析方法,该方法主要用于描述非线性系统的变化过程[21]。本文采用相空间重构法,将OLTC实测振动信号从一维变化为高维,在重构过程中,同时包含振动信号其他变量的变化特征,并且可以从其中一个分量的变化过程中构建和恢复整个振动信号的变化规律和特征。具体定义如下所示。
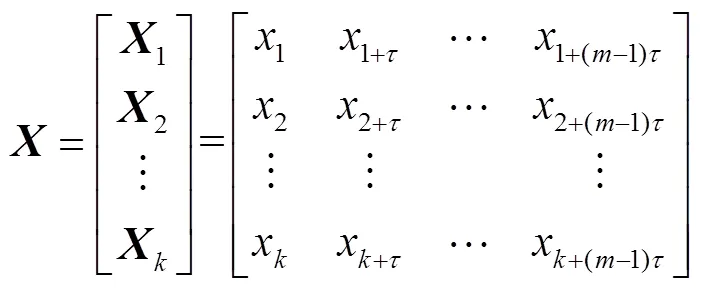
式中,为延迟时间;为嵌入维数;为个维向量构成的振动信号相轨迹,且和之间关系为
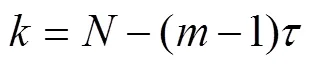
本文采用互信息值法[22]和Grassberger- Procaccia提出的P-G算法[23],分别计算OLTC的延迟时间[24]和嵌入维数。其中,嵌入维数采用P-G计算过程如下。
(1)利用式(1)的振动时间序列进行重构,其中的个数由式(2)确定。
(2)计算关联函数
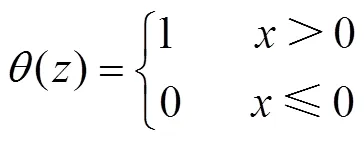
(3)对于某个的适当范围,重构信号的关联维数与累积分布函数()满足线性对应关系,表示为
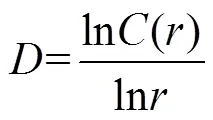
正常工况下的延迟时间和嵌入维数的变化趋势分别如图1和图2所示。其中图1的延迟时间是通过互信息值法计算的,通常将曲线中第一个极小值点对应的横坐标作为延迟时间。图2为OLTC切换过程测得的振动信号得到的ln()随ln的变化曲线,对应的是振动信号的嵌入维数=1~9的变化曲线,当=3时,曲线的线性部分不再变化,而且当=4以上时,无法通过几何图形直观地观察出各个振动模式,因此取=3。
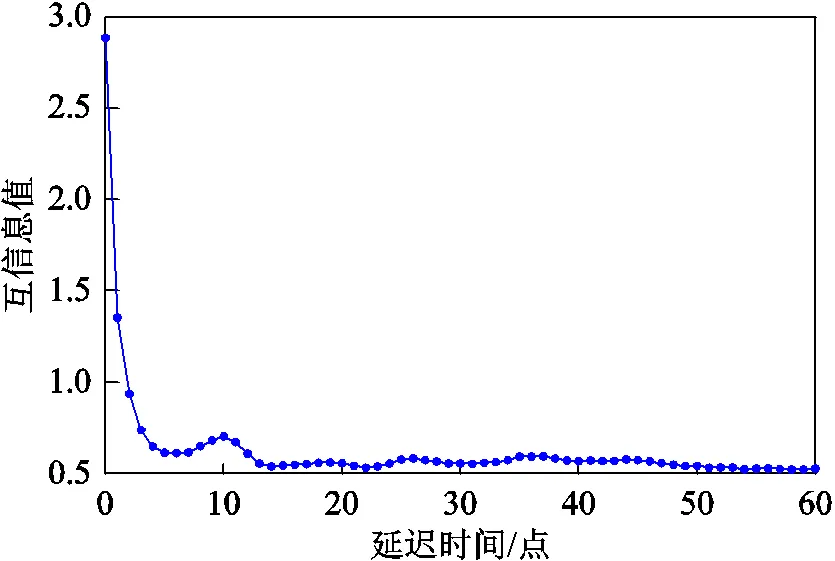
图1 OLTC振动信号的互信息值
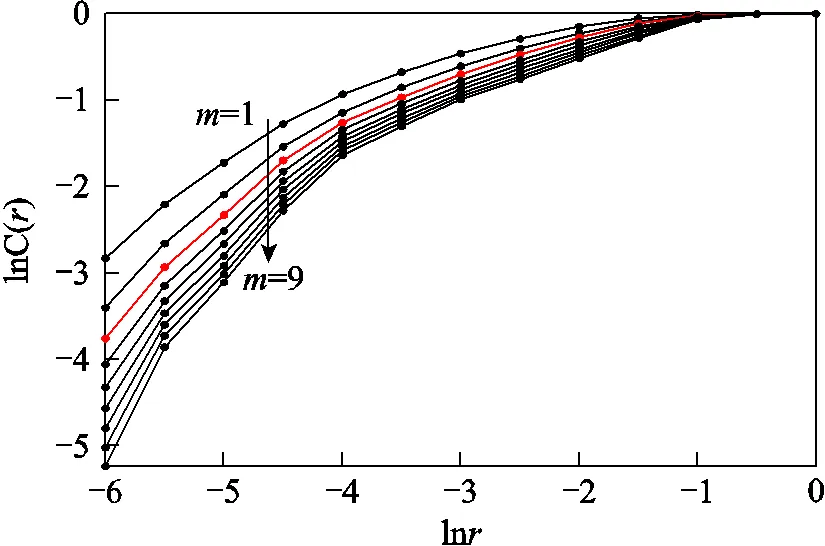
图2 lnC(r)随lnr的变化曲线
2 基于GOA优化K-means聚类算法
传统的K-means聚类算法是由MacQueen 于1967年首次提出的[25-26]。由于K-means算法对聚类中心的初始位置和离群点比较敏感,导致算法精度较低等缺陷,所以本文将GOA算法引入K-means算法中,对该算法的聚类中心进行改进。
2.1 蝗虫优化算法
根据蝗虫算法中蝗虫在自然界中的种群迁移和觅食行为将搜索分为开发和勘探,采用数学模型对该过程进行模拟,表示为[14]
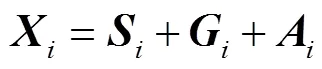
式中,为蝗群中的第只蝗虫的位置;为第只蝗虫收到其他蝗虫的互动力的影响;为第只蝗虫受到的重力影响;为第只蝗虫受到的风力影响。如考虑随机环境因素的影响,则式(5)改为
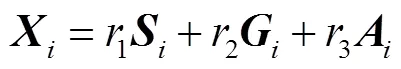
式中,1、2和3的取值为[0,1]间的随机数。
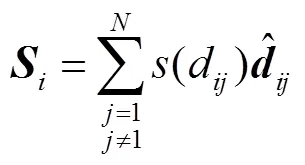
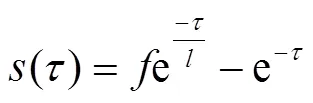
式中,和分别为吸引强度参数和吸引尺度参数,二者的取值情况决定参数的分布情况。通常取=1.5、=0.5。
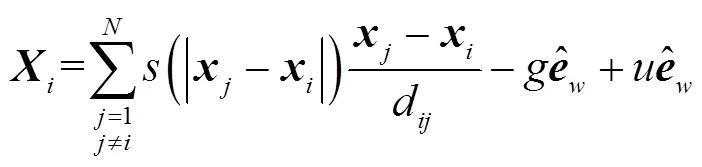
由于蝗虫更新位置不考虑重力和风力的影响,位置更新由蝗虫的当前位置、目标值位置和其他蝗虫位置共同决定,因此式(9)变为
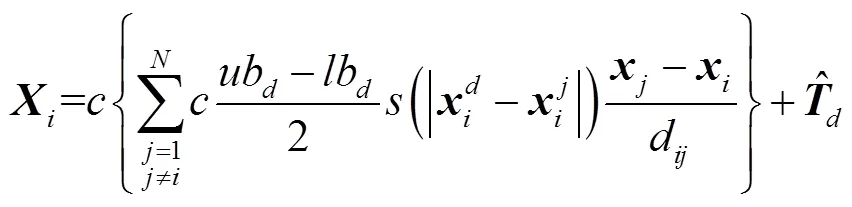
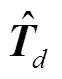
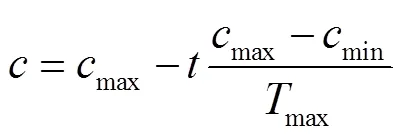
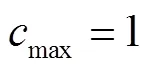
2.2 算法步骤
为了进一步地优化K-means算法的初始聚类中心,优化目标函数为
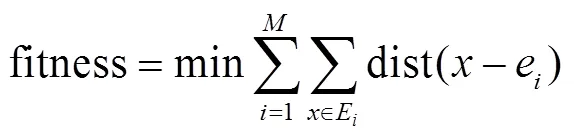
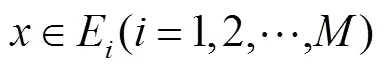
(1)GOA算法参数初始化。算法的最大迭代次数max,蝗群的种群数量、种群维数,以及参数max和min。
(2)利用随机化的方法生成初始蝗群位置。
(3)将式(12)作为适应度函数计算蝗虫个体的适应度值,并将最优适应度值的位置作为目标位置。
(4)利用式(10)对搜索个体进行位置更新。
(5)如果迭代次数>max,则算法终止,输出最优解;反之则回到步骤(3)。

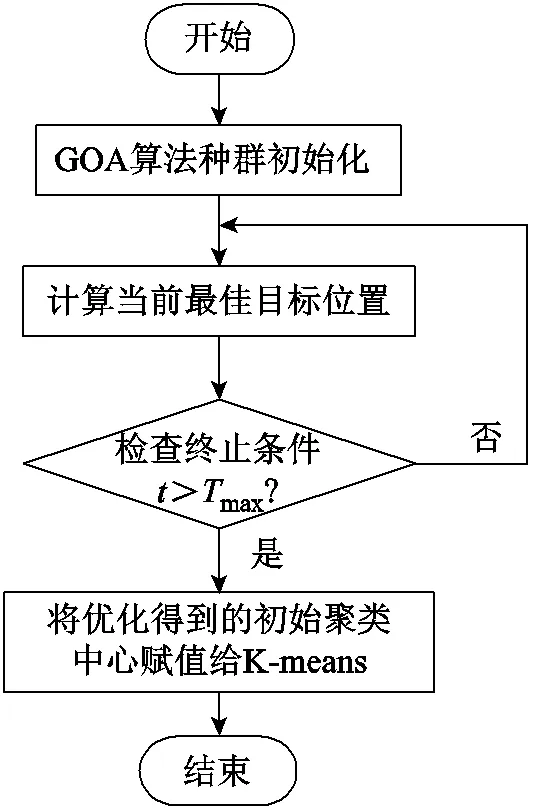
图3 GOA-K-means流程
3 OLTC振动信号的现场测试
本文采用型号CM111-50-63B-10193W华明M型有载分接开关,传感器的类型为传统压电式传感器与电荷放大器基于一体的LC0151型传感器,该传感器具有分辨率高、抗干扰能力强和噪声小等优点。
采集切换过程中的触头在不同工况下的振动信号,信号采样频率为50kHz,触头切换时间约为100ms,频率集中在20kHz以内,采样取6 873个点,切换时间集中在0~41ms,将加速度传感器安装在离振源比较近的地方,综合考虑安装在有载分接开关的顶上,并通过数据采集卡将振动信号转换为数字信号存储于计算机。加速度传感器具体安装位置如图4所示。

图4 OLTC故障试验
4 实验结果分析
4.1 相空间结果分析
在对信号进行具体分析时,首先将信号进行归一化处理,将正常工况下的平均幅值作为基准,其他工况下的振动信号乘以对应的归一化系数,使得不同工况下的平均振动幅值保持一致。归一化只改变信号幅值大小,不改变信号幅值对结果的影响,可以保留信号的完整性。
OLTC的相空间重构如图5所示。由图5可知,根据重构信号的相轨迹图的动力特性,当OLTC机械状态发生变化时,相轨迹的分布状况也会随之发生改变。其中正常工况下振动信号重构时的延迟时间和嵌入维数分别为=6和=3,触头脱落工况下振动信号重构时的延迟时间和嵌入维数分别为=17和=3,触头松动工况下振动信号重构时的延迟时间和嵌入维数分别为=6和=3,触头烧损工况下振动信号重构时的延迟时间和嵌入维数分别为=7和=3。
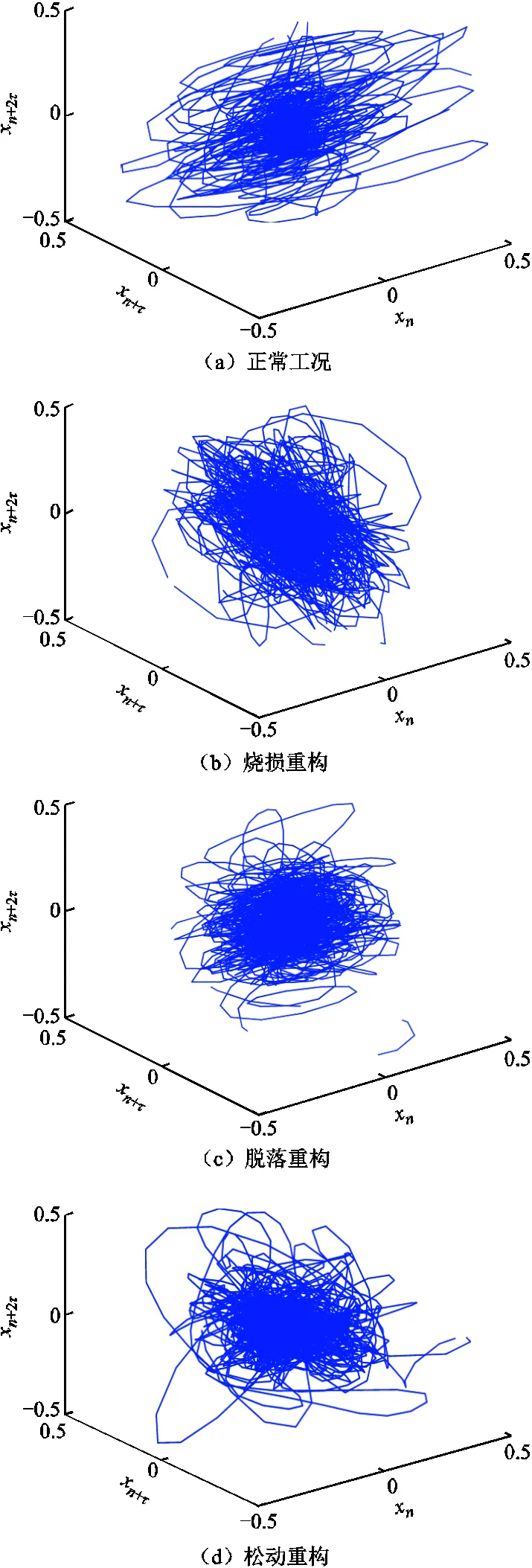
图5 OLTC的相空间重构
4.2 Kolmogorov熵混沌特性判断
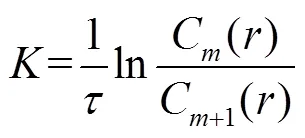
式中,为Kolmogorov熵;为延迟时间;C()和C1()分别为第维和第+1维的关联积分函数。实际计算中通常将随变化的稳定值作为Kolmogorov熵的估计值。
表1 Kolmogorov熵计算结果
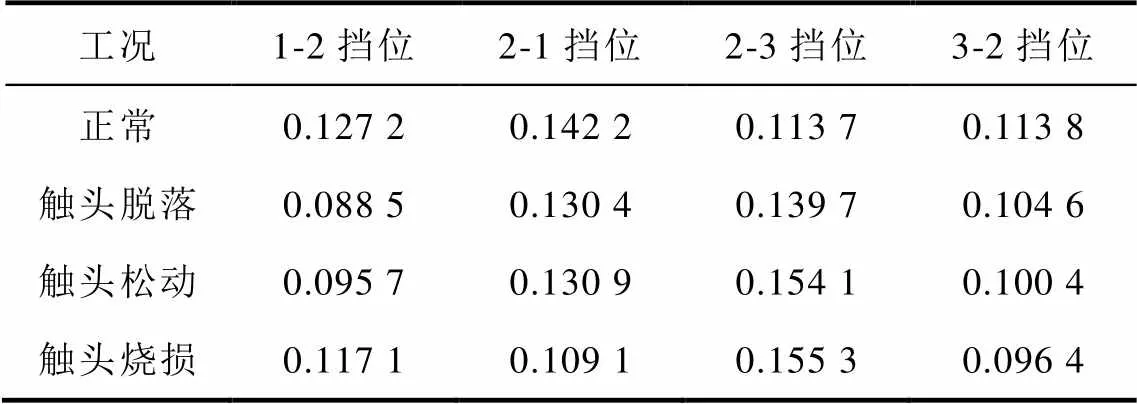
Tab.1 Calculations of Kolmogorov entropy
表1为OLTC在四种不同工况下四个档位的振动信号的Kolmogorov熵的计算结果。由表1中可以看出,Kolmogorov熵均为正,进一步证明了OLTC切换过程中产生的振动具有混沌特性。
4.3 K-means结果分析
本文选取聚类中心的个数=2,3,4,5,6,7,8,得到簇中心总体距离如图6所示,簇中心整体距离均随簇中心数目的增加而减小,当>3时其总体距离明显减缓,考虑综合因素确定簇中心个数为=4。图7表示四类不同工况的聚类中心相空间分布位置。通过图7,可以得出基于K-means方法的簇类中心原点距离之和。
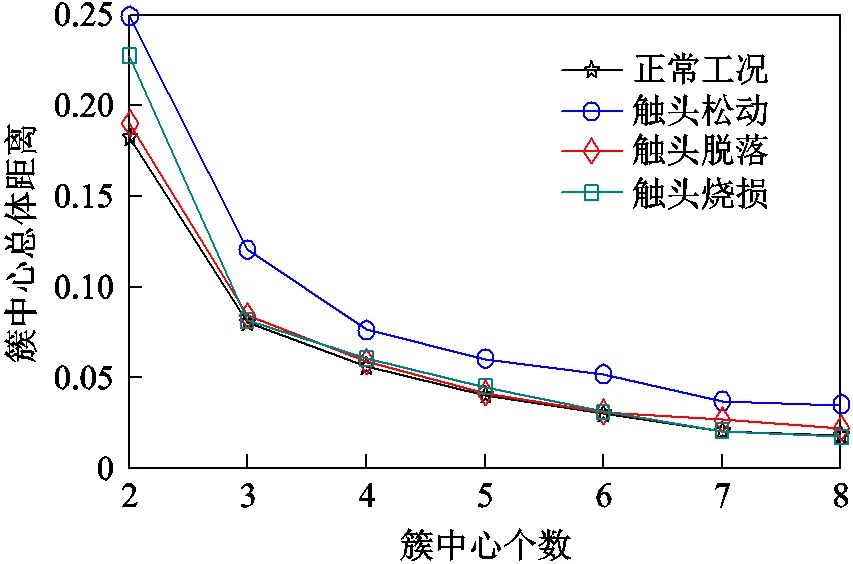
图6 总体距离曲线
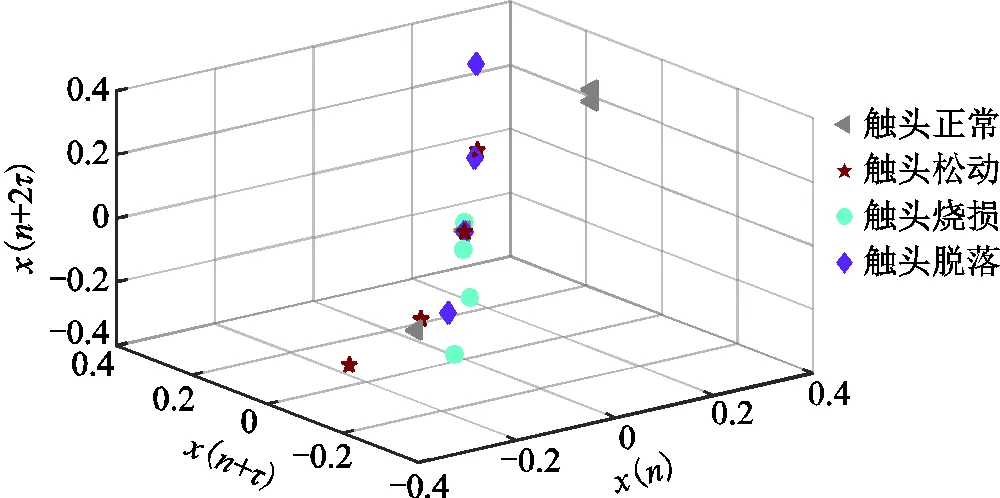
图7 聚类中心相空间位置
表2和表3分别为GOA-K-means的计算结果和传统的K-means计算结果。依据簇中心向量之和,相对于传统方法的K-means而言,GOA-K-means得出的计算结果呈现出规律性的变化:距离之和最大为正常工况,距离之和最小为松动,烧损和脱落的距离之和位于中间。从表2可以进一步看出,当距离之和大于1.1时为正常工况;当距离之和小于1.1时为故障,其中故障最为明显的是触头脱落和触头烧损。当距离之和在0.9~1时为触头脱落状态;当距离之和在0.6~0.7时为触头松动状态;当距离之和在1~1.1时为烧损状态,主要是由于有载分接开关在档位切换时,静动触头受力不均衡,正常状态下的受力大于烧损和松动导致的。烧损状态和正常状态差别不大,主要是由于烧损状态的面积不大,从而导致触头受力变化不同,呈现出的规律也不相同。
表2 GOA-K-means方法簇类中心原点距离之和
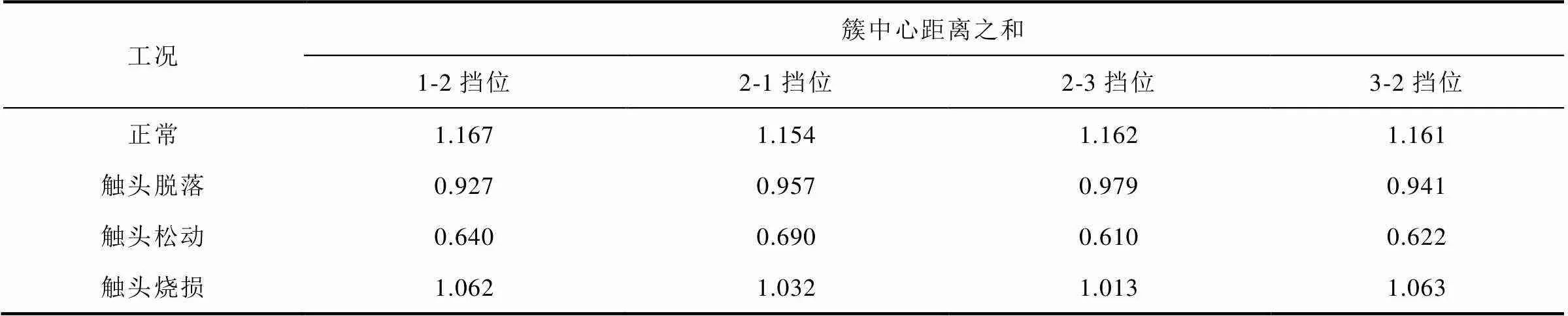
Tab.2 GOA-K-means method for the sum of central origin distances of clusters
表3 传统的K-means方法簇类中心原点距离之和

Tab.3 The sum of the origin distances of cluster central in the traditional K-means method
5 结论
本文为提高OLTC监测诊断精度,对K-means算法的初始聚类进行优化,提出一种基于GOA优化K-means的聚类算法,对实测的重构OLTC振动信号进行识别,研究结果表明:
1)根据OLTC开关切换过程中振动信号的混沌动力学特性,设置典型故障,计算延迟时间和嵌入维数,将实测振动信号在高维空间进行重构,使用Kolmogorov熵验证OLTC的混沌特性,得到振动信号的相空间分布特征,为OLTC的机械故障状态监测提供了更为丰富的信息源。
2)分别采用GOA-K-means算法和传统的K-means算法进行计算,得到OLTC振动信号相空间分布的特征向量簇中心,结果表明:采用GOA-K-means得出的结果呈现出规律性的变化,能较好地区分不同工况下的故障,该分析结果为及时发现OLTC的故障隐患提供了理论依据。
[1]姜益民. 上海电网有载分接开关运行分析[J]. 上海电力, 2006, 19(4): 386-394. Jiang Yimin. Analysis of OLTC running in shanghai power grid[J]. Shanghai Electrical Power, 2006, 19(4): 386-394.
[2]Bengtsson C. Status and trends in transformer monitoring[J]. IEEE Transactions on Power Delivery, 1996, 11(3): 1379-1384.
[3]Simas F E F, de Almeida L A L, de C Lima A C. Vibration monitoring of on-load tap changers using a genetic algorithm[C]//IEEE Instrumentation & Measurement Technology Conference, Ottawa, Ont, Canada, 2005: 2288-2293.
[4]张燕, 方瑞明. 基于油中溶解气体动态网络标志物模型的变压器缺陷预警与辨识[J]. 电工技术学报, 2020, 35(9): 2032-2041. Zhang Yan, Fang Ruiming. Fault detection and identification of transformer based on dynamical network marker model of dissolved gas in oil[J]. Transactions of China Electrotechnical Society, 2020, 35(9): 2032-2041.
[5]Yang Ruilin, Zhang Dandan, Li Zhenbiao, et al. Mechanical fault diagnostics of power transformer on-load tap changers using dynamic time warping[J]. IEEE Transactions on Instrumentation and Measurement, 2019, 68(9): 3119-3217.
[6]杨森, 陈莎莎, 李冠, 等. 基于变分模态分解与特征选择的变压器有载分接开关机械故障诊断[J].南方电网技术, 2019, 13(1): 39-47, 59. Yang Sen, Chen Shasha, Li Guan, et al. Mechanical fault diagnosis of transformer on-load tap-changer based on variational mode decomposition and feature selection[J]. Southern Power Systems Technology, 2019, 13(1): 39-47, 59.
[7]张静, 张丹丹, 程林, 等. 基于振动信号的有载分接开关故障模拟试验研究[J]. 高压电器, 2018, 54(10): 97-105. Zhang Jing, Zhang Dandan, Cheng Lin, et al. Experimental research on fault simulation of on⁃load tap changer based on vibration signals[J]. High Voltage Apparatus, 2018, 54(10): 97-105.
[8]Bengtsson C, Kols H, Martinsson L, et al. Acoustic diagnosis of on tap changers[C]//CIGRE 1996 Session, France: CIGRE, 1996: 32-INT-CANADA- 12-1.
[9]Rivas E, Burgos J C, Garcia-Prada J C. Condition Assessment of power OLTC by vibration analysis using wavelet transform[J]. IEEE Transactions on Power Delivery, 2009, 24(2): 687-694.
[10]Li Qingmin, Zhao Tong, Zhang Li, et al. Mechanical fault diagnostics of onload tap changer within power transformers based on hidden Markov model[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 596-601.
[11]赵彤, 张黎, 李庆民. OLTC振动信号的多维空间相轨图几何特征[J]. 高电压技术, 2007, 33(8): 102-105. Zhao Tong, Zhang Li, Li Qingming. Feature analysis methodology for phase portrait structure of mechanical vibration signals of on-load tap changers, multidimensional space[J]. High Voltage Engineering, 2007, 33(8): 102-105.
[12] 张知先, 陈伟根, 汤思蕊, 等. 基于互补集总经验模态分解和局部异常因子的有载分接开关状态特征提取及异常状态诊断[J]. 电工技术学报, 2019, 34(21): 4508-4518. Zhang Xianzhi, Chen Weigeng, Tang Sirui, et al. State feature extraction and anomaly diagnosis of on-load tap-changer based on complementary ensemble empirical mode decomposition and local outlier factor[J]. Transactions of China Electro tech nical Society ,2019,34(21):4508-4518.
[13]周翔, 王丰华, 傅坚, 等. 基于混沌理论和K-means聚类的有载分接开关机械状态监测[J]. 中国电机工程学报, 2015, 35(6): 1541-1548. Zhou Xiang, Wang Fenghua, Fu Jian, et al. Mechanical condition monitoring of on-load tap changers based on chaos theory and K-means clustering method[J]. Proceedings of the CSEE, 2015, 35(6): 1541-1548.
[14]Saremi S, Mirjalili S, Lewis A. Grasshopper optimisation algorithm: theory and application[J]. Advances in Engineering Software, 2017, 105: 30-47.
[15]Mirjalili S Z, Mirjalili S, Saremi S, et al. Grasshopper optimization algorithm for multi-objective optimization problems[J]. Applied Intelligence, 2017, 48(8): 805-820.
[16]Mafarja M, Aljarah I, Heidari A A, et al. Evolutionary population dynamics grasshopper algorithm approaches for feature selection problems[J]. Knowledge Based Systems, 2018, 145: 25-45.
[17]闫旭, 叶春明. 混合蝗虫优化算法求解作业车间调度问题[J]. 计算机工程与应用, 2019, 55(6): 257-264. Yan Xu, Ye Chunming. Hybrid grasshopper optimization algorithm for job-shop scheduling problem[J]. Computer Engineering and Applications. 2019, 55(6): 257-264.
[18]程泽新, 李东生, 高杨. 基于蝗虫算法的无人机三维航迹规划[J]. 飞行力学, 2019, 37(2): 46-50. Chen Zexin, Li Dongsheng, Gao Yang. UAV three-dimensional path planning based on the grasshopper algorithm[J]. Flight Dynamics, 2019, 37(2): 46-50.
[19]潘峰, 孙红霞. 基于蝗虫算法的图像多阈值分割方法[J]. 电子测量与仪器报, 2019, 33(1): 149-155. Pan Feng, Sun Hongxia. Algorithm for image segmentation based on grasshopper optimization algorithm[J]. Journal of Electronic Measurement and Instruments, 2019, 33(1):149-155.
[20]Zhang Xin, Miao Qiang, Zhang Heng, et al. A parameter-adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery[J]. Mechanical Systems and Signal Processing, 2018, 108: 58-72.
[21]李恩文,王力农,宋斌,方雅琪.基于混沌序列的变压器油色谱数据并行聚类分析[J]. 电工技术学报, 2019, 34(24): 5104-5114. Li Enwen , Wang Linong, Song Bin, eta al. Parallel clustering analysis of dissolved gas analysis data based on chaotic sequences[J].Transactions of China Electrotechnical Society, 2019, 34(24): 5104-5114.
[22]吕金龙, 陆君安, 陈士华. 混沌时间序列分析及其应用[M]. 武汉: 武汉大学出版社, 2001.
[23]Albano A M, Muench J, Schwartz C, et al. Singular value decomposition and the grassberger-procaccia algorithm[J]. Physical Review A, 1988, 38(6): 3017-3026.
[24] 郭伯和, 金宁德, 胡亚范, 等. 油水两相流流型的混沌时间序列分析[J]. 动力学与控制学报, 2004, 2(3): 50-55. Guo Baihe, Jin Ningde, Hu Yafan, et al. Chaotic time series analysis of oil/water two phase flow patterns[J]. Journal of Dynamics and Control, 2004, 2(3):50-55.
[25]钱瑾, 王培红, 李琳. 聚类算法在锅炉运行参数基准值分析中的应用[J]. 中国电机工程学报, 2007, 27(23): 71-74. Qian Jin, Wang Peihong, Li Lin. Application of clustering algorithm in target-value analysis for boiler operating parameter[J]. Proceedings of the CSEE, 2007, 27(23): 71-74.
[26]杨雨航. 动态粒子群优化K-means的图像分割算法研究[J]. 现代计算机, 2019(8): 63-67. Yang Yuhang. Image segmentation algorithm based on improved particle swarm optimization and K-means clustering[J]. Modern Computer, 2019(8): 63-67.
[27]Grassberger P, Procaccia I. Estimation of the Kolmogorov entropy from a chaotic signal[J]. Physical Review A, 1983, 28(4): 2591-2593.
Analysis and Calculation Method of On-Load Tap Changers State Characteristics Based on Chaos Theory and Grasshopper Optimization Algorithm-K-means Algorithm
Ma Hongzhong Yan Yan
(College of Energy and Electrical Engineering Hohai University Nanjing 211100 China)
To monitor the mechanical state of on-load tap changer (OLTC) more accurately and effectively, considering the situation that the clustering effect of traditional monitoring methods based on K-means are affected by the selection of their initial clustering centers, this paper proposed an OLTC mechanical state monitoring method based on the combination of grasshopper optimization algorithm (GOA) and K-means. Firstly, on account of the nonlinear and chaotic characteristics of OLTC vibration signals, the embedding dimension and delay time are calculated by the P-G method and mutual information value method, and the phase space of the measured OLTC vibration signals was reconstructed. Secondly, Kolmogorov entropy was applied to judge the chaotic characteristics of the reconstructed vibration signals. Finally, to improve the clustering accuracy, according to the sensitivity of K-means to the initial clustering center, GOA was introduced into the algorithm to optimize its clustering center, and the reconstructed high-dimensional vibration signals were analyzed by an optimized K-means clustering method. The results showed that in the application of OLTC vibration signal identification, the calculation results obtained by the optimized K-means clustering algorithm have certain regularity, which provides a new way for OLTC machines running state monitoring.
Grasshopper optimization algorithms, on-load tap-changer, optimized K-means, vibration signal
TM403.4
10.19595/j.cnki.1000-6753.tces.201174
2020-09-03
2020-10-13
马宏忠 男,1962年生,博士,博士生导师,研究方向为电力设备状态监测、故障诊断与健康预警。E-mail:hhumhz@163.com
严 岩 男,1990年生,博士研究生,研究方向为电力设备故障诊断、电力系统建模。E-mail:yanyan503986706@163.com(通信作者)
(编辑 郭丽军)
