滚仰式导引头稳定和跟踪特性研究*

陈思远，谢 伟，刘石祥，王以波

（1. 西南电子设备研究所，四川 成都610036；2. 北京理工大学机电学院，北京100081）

引 言

滚仰式红外导引头采用滚转外框、俯仰内框结构，实现了±90°框架角，使导引头视场可以覆盖整个前半球，为导弹实现大离轴角发射提供了必要条件[1]。同时，滚仰式导引头采用捷联稳定控制平台，平台上不安装惯性器件并将探测器置于弹体上，既减小了导引头的体积和质量，又改进了弹体气动性能，并已在美国的AIM-9X和欧洲的IRIS-T得到了应用[2]。

国内在先进空空导弹发展的需求牵引下，对滚仰导引头控制技术开展了研究。文献[3–4]分别采用坐标转换和旋量理论研究了滚仰导引头跟踪目标时的框架角增量计算方法，根据框架角和探测器误差角实现滚仰导引头控制闭环。文献[5]研究了一种跟踪回路角增量优化方法。文献[6–7]分析了滚仰导引头过顶奇异性问题，并提出了分段控制的奇异性控制策略。文献[8–9]采用重构视线角的方法研究了滚仰导引头视线角速度提取。

目前关于滚仰导引头控制技术的研究集中在过顶跟踪策略及视线角速度提取上，关于弹体扰动对滚仰导引头稳定和跟踪的研究很少。本文首先研究了弹体扰动对滚仰导引头的影响，分析了导引头完全隔离弹体扰动的条件，最后通过数值仿真，对滚仰导引头隔离弹体扰动的能力和跟踪目标时光轴惯性空间的运动进行了分析。

1 滚仰导引头稳定特性分析

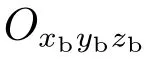
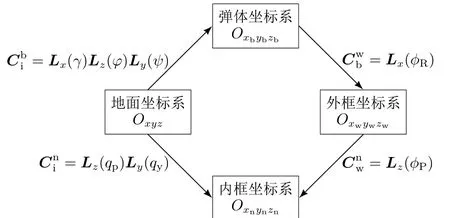
图1 坐标转换关系

图1中：φ为俯仰角；γ 为滚转角；ψ为偏航角；qp为视线高低角；qy为视线方位角；φR为外框框架角；φP为内框框架角；旋转矩阵Lx(ε)，Ly(ε)，Lz(ε)分别表示以角度ε绕x轴、y轴和z轴旋转的矩阵：

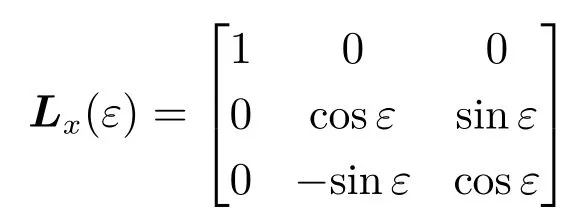
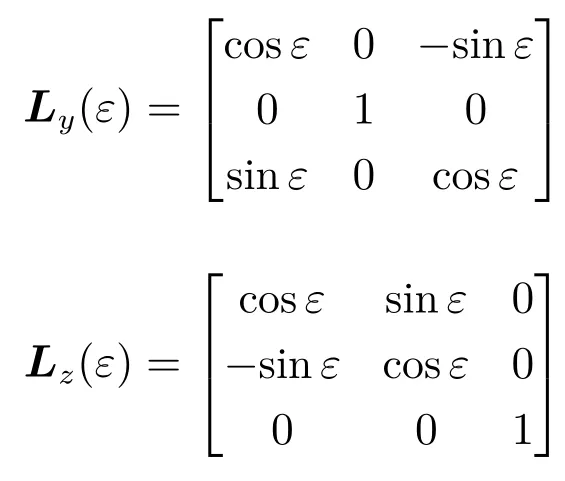
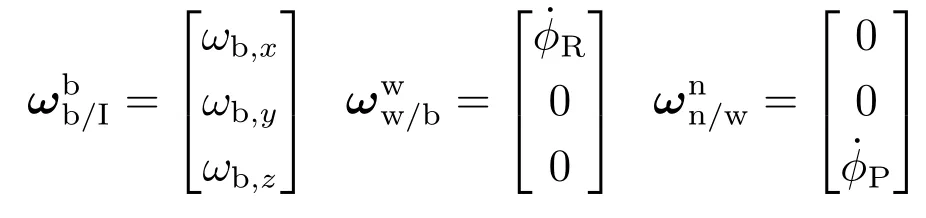
式中：ωb,x,ωb,y,ωb,z为弹体相对于惯性空间的角速度；˙φR和˙φP为导引头框架角速度。

则由坐标转换关系可得：

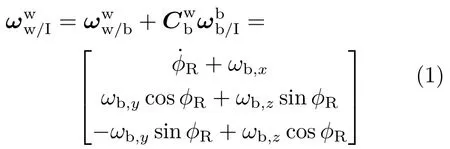
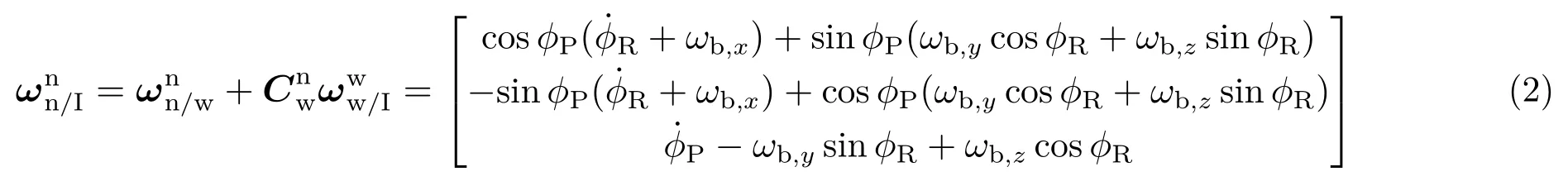
考虑框架轴承光滑，无扰动力矩，滚转轴承可有效隔离弹体滚转通道的扰动，使得滚转框相对于惯性空间在x方向的角速度为0，即：

同理，俯仰框轴承可有效隔离弹体内框俯仰方向的弹体扰动，使得内框相对于惯性空间在z 方向的角速度为0，即：

式（3）和式（4）是导引头轴承结构自动满足的条件，不需要添加控制力矩。内框相对于惯性空间的角速度在z轴上被完全隔离，而在y轴上的分量不一定能隔离。当导引头视线稳定时，需要满足内框相对于惯性空间在z方向和y方向的视线角速度都为0，即：

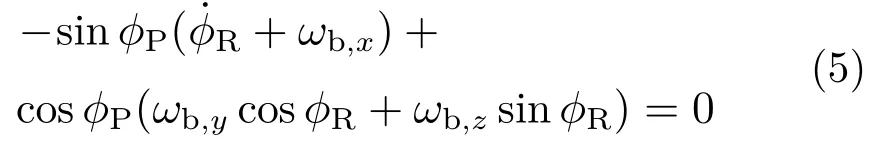
由式（5）可以计算得到：

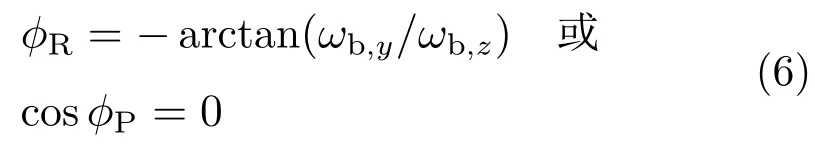
当俯仰框架角为90°时，或者滚转框架角为−arctan(ωb,y/ωb,z)时，内框y方向才能保持稳定。

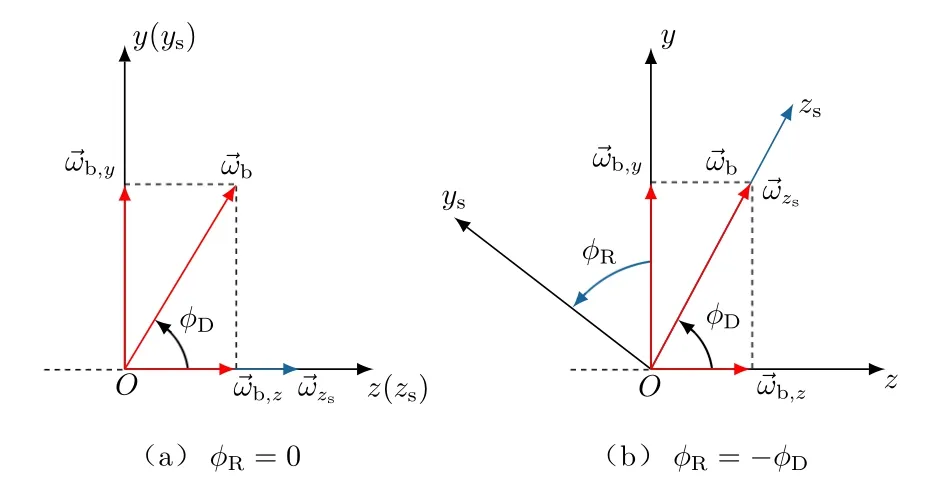
图2 弹体扰动示意图

2 半捷联稳定控制方案

滚仰导引头根据探测器测量得到的相对于内框y，z 轴的目标角偏差εy和εz，结合当前滚转框架角φR和俯仰框架角φP，计算得到滚转框架角误差指令∆φR和俯仰框架角误差指令∆φP，从而驱动框架伺服机构来降低框架角误差。框架角误差指令可通过坐标转换[3]以及矢量理论[4]求解得到，本文采用文献[3]中的方法进行框架角跟踪指令计算，计算式如式（7）所示。

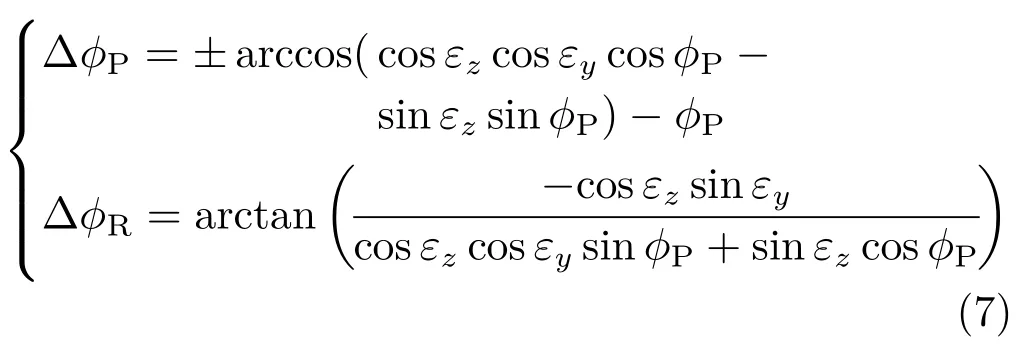
为了降低滚仰导引头的重量和体积，结合其跟踪特性，采用半捷联稳定控制方案，俯仰和滚转框都采用外回路框架角反馈，内回路采用框架角速度反馈控制。俯仰框外回路反馈为俯仰框架角，内回路反馈为俯仰框电机输出角速度。俯仰框反馈可采用弹体角速度与俯仰框架角速度组合得到，其表达式为：

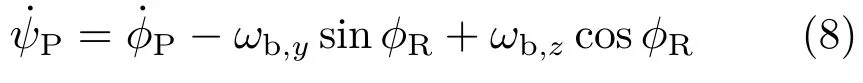
滚转框外回路反馈为滚转框架角，内回路反馈为滚转框电机输出角速度。滚转框反馈等于框架角速度与弹体角速度之和，其表达式为：

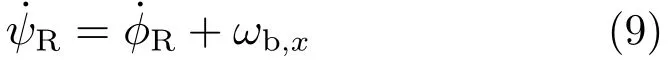
根据稳定回路分析，假设初始探测器误差角为0。导引头可完全隔离滚转扰动，此时˙ψR= 0；当滚转框架角φR=−arctan(ωb,y/ωb,z)时，导引头可同时隔离俯仰和偏航扰动，此时˙ψP=0。

滚仰导引头半捷联稳定控制方案如图3所示。为了实现对目标的有效跟踪，需要滚转导引头的滚转框和俯仰框协同控制，将内框俯仰轴旋转至垂直于目标运动方向，此时期望的滚转角指令为φRC。而根据弹体扰动分析，只有当内框俯仰轴旋转至垂直于弹体俯仰和偏航扰动合矢量方向时才能完全隔离弹体扰动，此时的滚转角指令为φRD。当φRC与φRD不相等时，滚仰导引头不能同时实现对目标的跟踪和光轴在惯性空间的稳定。

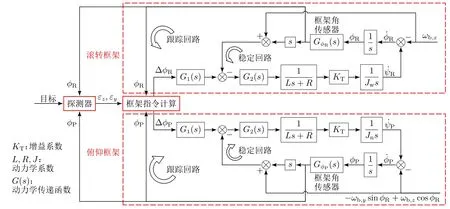
图3 半捷联稳定控制方案

3 光轴惯性空间运动

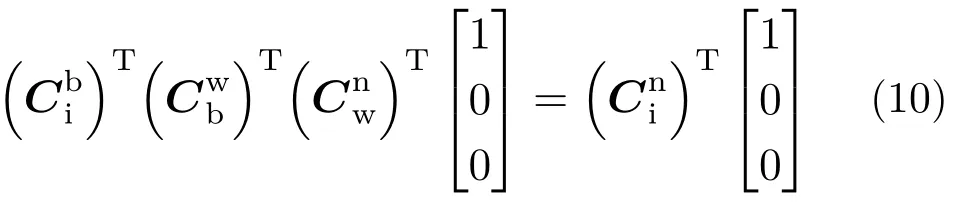
将坐标转换关系带入式（10），可以得到两种转换关系下的光轴在惯性空间的坐标。设由式（10）左边第一种路径得到的坐标为[a b c]T，由第二种路径得到的坐标为[cos qpcos qysin qp−cos qpsin qy]T，则有：

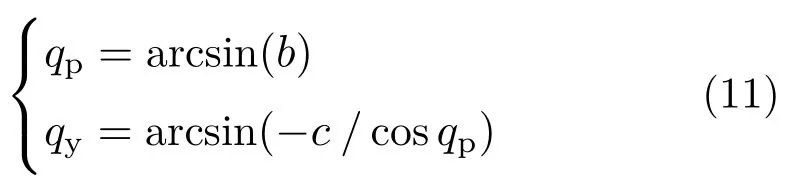
通过式（11）可以计算得到导引头光轴在惯性空间的角度qp和qy。导引头光轴在惯性空间对目标进行跟踪，其运动还受到弹体扰动的影响，当光轴无法完全隔离弹体扰动时，光轴的运动角速度与视线角速度并不相等，无法直接提取视线角速度信息。

4 数值仿真分析

4.1 仿真条件

为了简化仿真，俯仰框和滚转框控制采用相同的控制结构，外回路等效增益为K1，内回路等效增益为K2。等效闭环传递函数为：

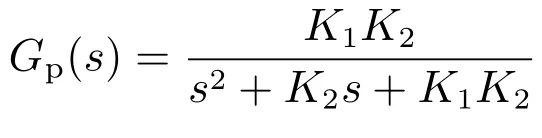
选取俯仰框控制系统增益为K1= 12.56，K2=125.60。选取滚转框K1分别为12.56，18.85，31.42，62.83，K2取为125.60，分析导引头滚转框快速性对隔离弹体扰动以及目标跟踪的影响。

4.2 隔离弹体扰动

初始时刻光轴指向目标，目标固定。弹体偏航方向扰动角速度ωb,y= 1 (°)/s，此时得到的光轴和框运动如图4—图7所示。

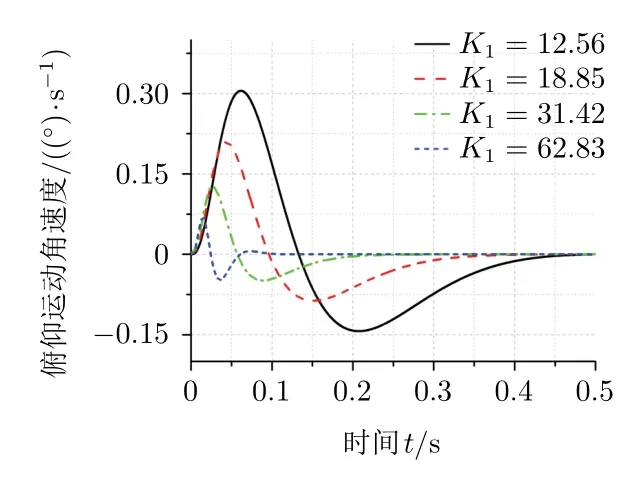
图4 光轴惯性空间俯仰运动角速度

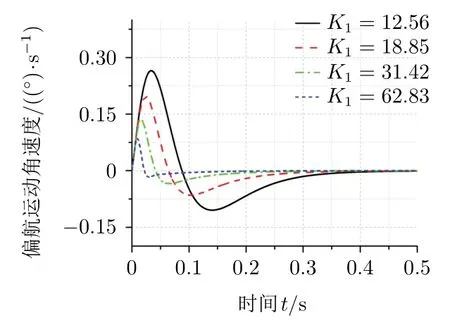
图5 光轴惯性空间偏航运动角速度

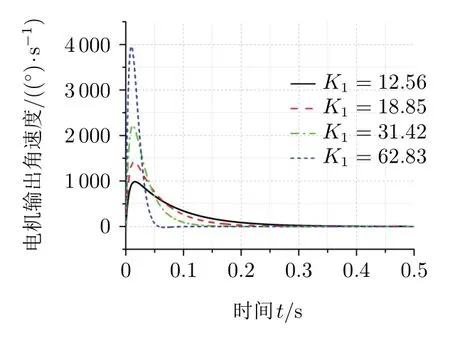
图6 滚转框速度输出

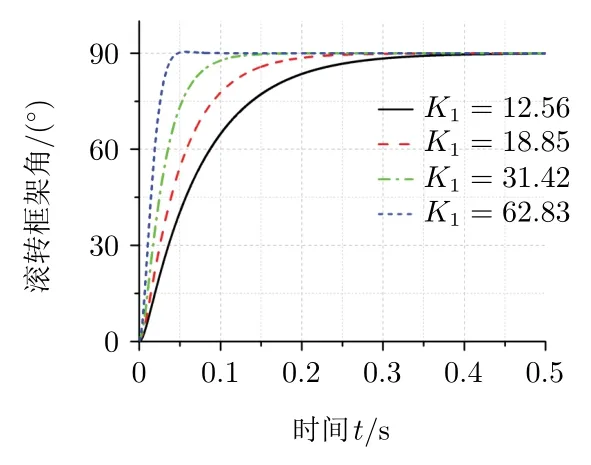
图7 滚转框架角

由图4—图7可以看出，当弹体只有偏航方向扰动时，完全隔离扰动的滚转框架角指令为90°，随着滚转框外回路增益K1的增大，滚转框架角响应速度加快，弹体偏航角速度带来的扰动和过渡过程时间逐渐减小，当滚转框架角滚转到90°时，可完全隔离偏航扰动。在滚转过程中，滚转电机输出角速度会达到极大值，且极大值与滚转外回路增益K1成正比，而实际中由于受到电机输出力矩的影响，如美国AIM-9X的电机框输出角速度为1 600(°)/s[7]，外回路增益K1不能取值太大。

4.3 跟踪能力分析

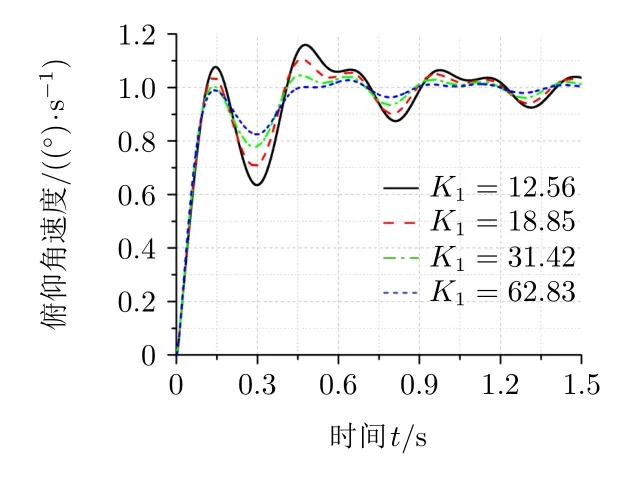
图8 光轴俯仰角速度

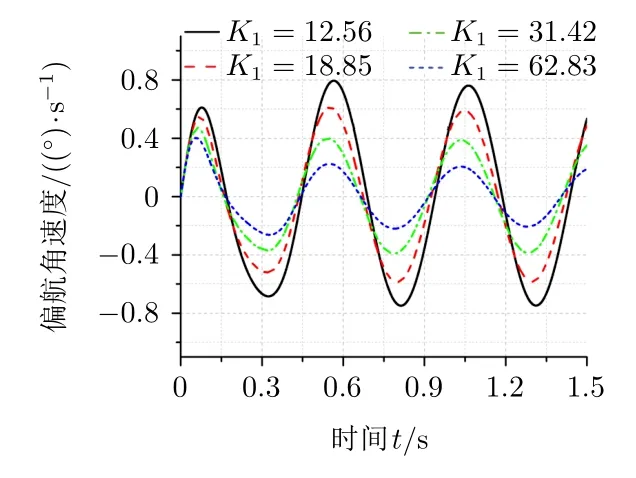
图9 光轴偏航角速度

由图8和图9可以看出，光轴俯仰角速度中含有弹体偏航扰动带来的影响，光轴偏航角速度随弹体做2 Hz的正弦变化。滚转框外回路增益K1越大，弹体偏航扰动对光轴俯仰角速度的影响越小，光轴偏航角速度正弦变化的幅值越小，导引头隔离弹体偏航扰动的能力越强。根据隔离弹体扰动的仿真结果可知，由于受到电机输出最大角速度的限制，滚转框外回路增益K1不能取值太大，而此时导引头无法隔离弹体扰动，其光轴运动特性与视线在惯性空间的运动规律存在很大差别，不能用光轴在惯性空间的角速度代替视线在惯性空间的角速度。

5 结束语

本文分析了弹体扰动对滚仰导引头的影响。滚仰导引头可以隔离弹体滚转和俯仰方向的扰动，隔离偏航方向扰动需要控制滚转框架角，而对目标的跟踪也需要滚转框架角控制，两者存在矛盾。这导致光轴运动中包含了弹体运动分量，滚转框响应速度越快，弹体扰动对导引头光轴的影响越小，而对滚转框电机输出角速度要求越高，限制了滚转框的快速性，此时导引头视线角速度提取方式与传统俯仰–偏航两框导引头完全不同，需要根据滚仰导引头半捷联稳定控制特点进行控制系统设计及视线角速度提取。