快充条件下18650锂离子电池热-力耦合分析

2021-04-13肖佳将

科学技术与工程 2021年7期

田晟, 肖佳将

(华南理工大学土木与交通学院, 广州 510640)

面对日益突出的环境和能源问题,发展电动汽车是实现汽车行业可持续发展最有潜力的解决方案之一。动力电池是电动汽车的主要储能部件,锂离子动力电池由于具有能量和功率密度高、自放电率低、容量大、寿命长等优势在电动汽车上得到了广泛应用[1-2]。锂离子电池在使用过程中伴随热量的释放,引起电池温升和温差,电池温度的变化会产生内部热应力,应力过大会造成电极材料粉化失效,隔膜压缩变形进而导致内阻增大[3],影响电池的安全性和使用寿命。

现阶段有关动力电池热效应的研究主要集中在电池热模型建立和成组热管理方面[4-5],对电池热应力方面的研究相对较少。Gao等[6]研究了锂离子电池锂锡合金负极应力-应变关系,以及随荷电状态变化时应力-应变关系的演变。Duan等[7]建立了锂离子电池电化学-热-力耦合模型,发现锂离子的嵌入是产生应力的主要原因,电极的最大应力是负极的环向应力。卢世刚等[8]、金标等[9]利用数值模拟,得到方形锂离子热应力场,电池中心受压应力,侧边受拉应力且侧边中心处出现热应力集中。熊瑞等[10]研究了外部短路故障情况下圆柱形锂离子电池内部的热应力分布,发现电池两端内部活性材料与壳体的接触部位产生最大热应力。

现以18650锂离子电池为研究对象,建立电池多阶段恒流充电条件下的热-力顺序耦合模型,对不同充电环境温度下的电池温度场和热应力场进行求解分析。

1 电池结构与生热模型

1.1 电池内部结构

18650锂离子电池的电芯部分是由正极、正极集流体、负极、负极集流体、隔膜组成,电池正极和负极之间有电解液,为正、负极之间离子迁移提供介质,各层材料按一定顺序组合通过卷绕形成圆柱状,具体结构如图1所示。

选用的18650锂离子电池基本参数如表1所示。

1.2 电池生热模型

1.2.1 导热微分方程

锂离子电池生热过程为非稳态的热传导过程,为简化模型,假设电池内部各物理性质均匀一致且保持不变,忽略电池内部热辐射和热对流。根据傅里叶导热基本定律和能量守恒定律,在柱坐标系

(r,θ,z)下18650锂离子电池的导热微分方程可表示为

(1)

式(1)中:ρ为电池密度,kg/m3；cp为电池比热容,J/(kg·K)；λr、λθ、λz分别为电池径向、周向和轴向导热系数,W/(m·K)；qV为电池生热速率,W/m3；Tb为电池温度，℃；t为时间，s。

1.2.2 热物性参数

电池的热物性参数为式(1)中的电池密度ρ、比热容cp和导热系数λr、λθ、λz,可由式(2)～式(5)计算获得。电池各部分组成材料的物理参数如表2[10-13]所示。

表2 电池各组成部分物理参数[10-13]Table 2 Physical parameters of each component of the battery[10-13]

ρ=m/Vb

(2)

(3)

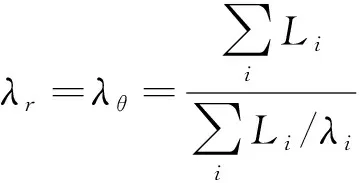
(4)

(5)

式中：m为电池质量,kg；Vb为电池体积,m3；ρi为电池各组分密度,kg/m3；Vi为电池各组分体积,m3；ci为电池各组分比热容,J/(kg·K)；Li为电池各层材料厚度,m；λi为电池各层材料导热系数,W/(m·K)。

计算得电池的平均密度为2 660.14 kg/m3,比热容为1 182.52 kg/K,各方向导热系数分别为λr=λθ=0.92 W/(m·K),λz=25.62 W/(m·K)。

1.2.3 生热速率

电池单体的生热速率采用Bernardi等[14]提出的公式，即

(6)

式(6)中：I为充放电电流,A；Eoc、U分别为电池开路电压和端电压,V；Tb为电池温度,取293.15 K；Rr、dEoc/dT分别为电池内阻和温度影响系数,常温下变化幅度很小一般可视为定值,分别取65.52 mΩ、2.410-4V/K[15]。

2 快充条件下电池温度场仿真

2.1 快充基础理论

现阶段关于电池充电方式的研究主要是基于美国科学家Mas提出的蓄电池可接受的充电电流曲线,如图2所示。

图2 电池可接受充电电流曲线Fig.2 Battery acceptable charging current curve

随着充电的进行,电池内部的活性物质不断减少,同时电池会产生极化现象阻碍充电进行[16],所以电池可接受的最大充电电流呈指数下降趋势,其表达式为

i=I0e-αt

(7)

式(7)中：I0为电池可接受的最大充电电流,由电池的使用状态决定；α为衰减常数,为时间t=0时电池可接受的充电电流I0与待充容量C之比,即α=I0/C。

充电电流若超过可接受充电电流曲线,不但不能提高充电速率,还会增加电池的析气量,加深极化现象；充电电流若低于该曲线,则会延长充电时间,因此最好使充电电流大小保持在曲线附近,以获得最短充电时间和最高充电效率。

2.2 多阶段恒流充电

多阶段恒流充电方法是将电流分为多个阶段给电池充电(一般不超发过5个),每一阶段达到设定的终止判断条件后减小电流进入下个充电阶段,能使充电电流很好地靠近电池可接受充电电流曲线,还能通过在每个充电阶段末加上放电脉冲很好地消除极化现象[17]。多阶段恒流充电的难点在于各阶段电流的取值和逻辑控制。参考文献[18]正交试验确定5阶段恒流充电各阶段电流大小为2.0C、1.65C、1.45C、1.2C、0.7C,如图3所示，以电压达到4.2 V作为阶段充电终止条件,并在每阶段充电末期加入2 s的1.0C放电去极化,34.5 min左右充入近92%的电量。

图3 5阶段恒流充电曲线Fig.3 Five-stage constant current charging curve

2.3 温度场仿真

利用Fluent对电池进行温度场仿真,忽略电池对外部的热辐射,只考虑电池内部的热量传递和电池表面与空气之间自然对流换热,取对流换热系数h=5 W/(m2·K),电池温度设为20 ℃,环境温度Te分别取20、25、30 ℃,电池生热速率根据各阶段的放电倍率由式(6)计算,环境温度为20 ℃时电池表面和中心截面温度分布云图如图4所示,不同环境温度下电池温升曲线如图5所示。

图4 环境温度20 ℃电池温度场分布Fig.4 Temperature field distribution of the battery under ambient temperature of 20 ℃

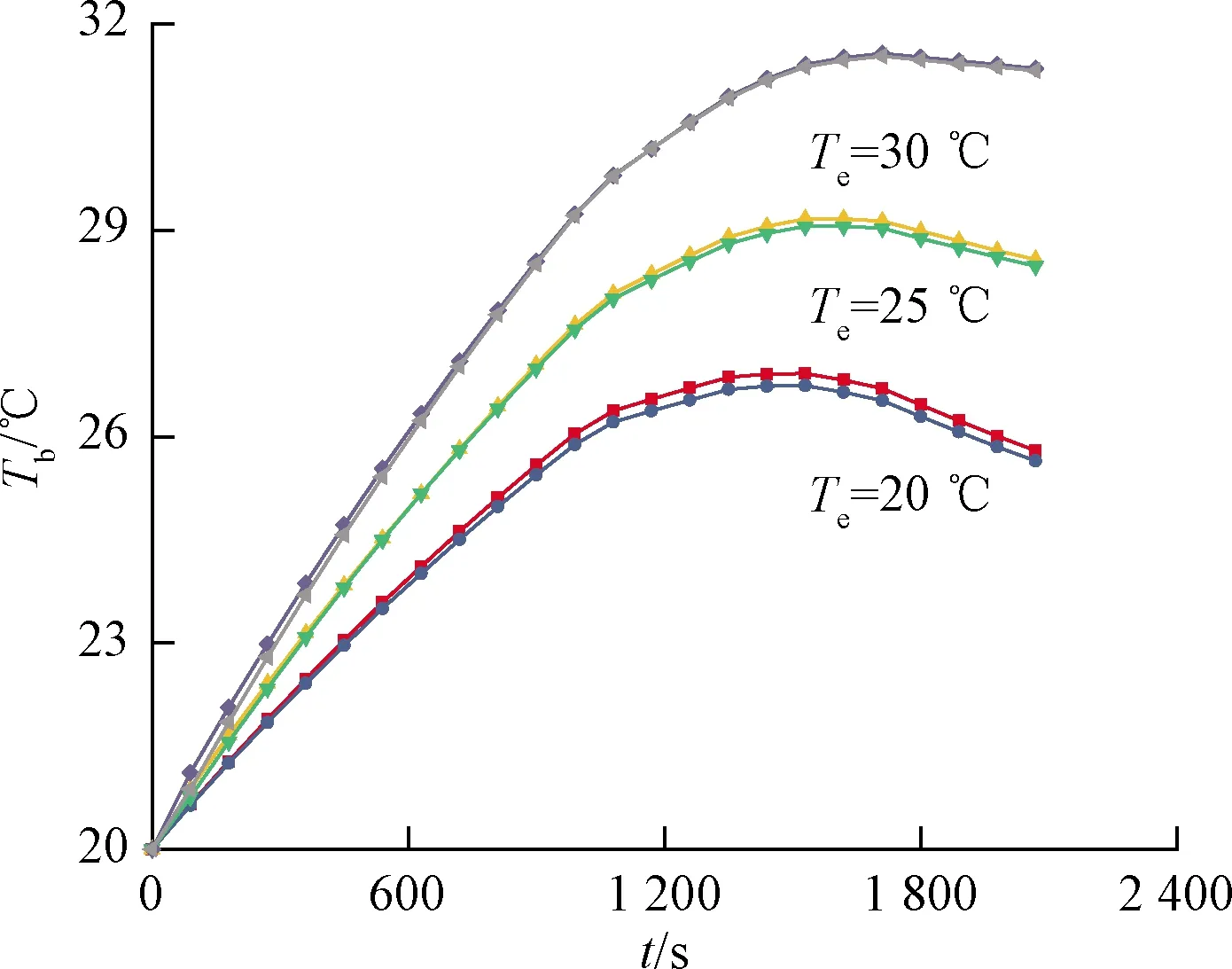
图5 不同环境温度下电池最高/最低温度温升曲线Fig.5 Maximum/minimum temperature rise curve of the battery under different ambient temperatures

从图4可以看出,电池的最高温度在中心部位,温度由内到外逐渐降低,电池两端面的最高温度比柱面最高温度要高,这是由于电池内部仅靠热传导进行传热,电池轴向导热系数大,热传导能力强,电池外表面与空气接触进行对流换热,散热条件更好。由图5可知,环境温度越高,电池的温升越大,温差越小,环境温度为20 ℃时,电池最高温度为25.79 ℃,温差为 0.15 ℃；当环境温度上升到30 ℃时,电池最高温度为31.35 ℃,温差为0.04 ℃。随着充电倍率的降低,电池温升速率逐渐降低,到充电后期,由于电池的发热量很小,电池散热能力高于产热能力,所以温度会出现稍微下降,降幅随环境温度的升高而减小。

3 电池热应力分析

3.1 电池热力学参数

锂离子电池温度的变化会产生热应力,且由于电池各层材料的热膨胀系数不同,温度变化引起各层材料的热膨胀不同也会产生热应力。假设构成电池的复合材料中各层材料力学性能都是各向同性,电池整体力学性能参数与热物性参数类似采用串并联计算,各材料力学性能参数如表2所示,结合复合材料细观力学和热膨胀理论,得到电池整体热力学参数如表3所示。

表3 电池力学参数Table 3 Mechanical parameters of battery

3.2 热应力仿真分析

将Fluent计算得到的电池温度求解结果作为应力分析载荷加载到力学分析模块Static Structural中有限元模型的节点上,建立顺序热-力耦合模型,添加约束条件并设置电池材料相关力学参数,仿真得到锂离子电池在不同环境温度下充电结束时的中心截面范式等效应力(Von Mises应力)分布如图6所示,总形变如图7所示。

由图6和图7可知,电池Von Mises应力分布不均,最大Von Mises应力出现在圆柱面外边的中间位置,最小Von Mises应力分布在电池轴向两端。电池最大形变发生在电池轴向两端,最小形变发生在电池中心区域,环境温度20 ℃时最大形变为1.5×10-3mm,最小形变为3.32×10-5mm。随着环境温度的升高,电池的总形变增大,电池的Von Mises应力逐渐往电池中心处集中,但最大Von Mises应力仍处于电池圆柱面外边的中间位置。当环境温度在20～30 ℃范围内时,随着环境温度升高,电池内部温差减小,Von Mises应力减小,最大Von Mises应力由241.91 kPa减小到28.98 kPa,应力差也减小,电池各处的应力趋向均匀。