含储能装置的园区综合能源系统三级协同规划设计方法

2021-04-13郑海雁薛溟枫唐一铭汪超群

科学技术与工程 2021年7期

郑海雁, 邹磊, 杨斌, 薛溟枫, 唐一铭, 汪超群

(1.江苏方天电力技术有限公司，南京 211102； 2.国网江苏省电力有限公司，南京 210024；3.国网江苏省电力有限公司无锡供电分公司，无锡 214061； 4.浙江大学电气工程学院，杭州 310007)

随着社会经济的快速发展，人类对于能源特别是化石能源的需求也越来越大。伴随而来的是能源危机的不断加剧和环境污染的日益恶化[1]。为此，人们迫切需要一种能源节约型和环境友好型的现代能源利用方式来替代传统高耗能高污染的能源供应体系。综合能源系统(integrated energy system，IES)[2-3]通过将多种能源利用和转化设备集成于一体，可以实现各类能源的梯级高效利用，被广泛认为是解决这两类问题的重要途径之一[4]。

目前，中国的综合能源系统建设和运营工作已全面展开，相关的技术和服务已开始造福社会。其中，具有代表性的示范项目包括北京延庆主动配电网项目、上海迪士尼度假区示范项目、天津中新生态城示范项目、江苏同里小镇综合能源服务示范区项目[5]以及无锡红豆工业园综合能源服务项目等。截止到2019年底，中国已投产和规划在建的各类综合能源项目多达2 000余个，全部建成后预计每年可节约标煤1 000万t，减少CO2排放近2 500万t。综合能源的大力推广和建设，以及自身具备的突出优势，预示着IES在未来的能源格局中将占据着至关重要的地位和作用，综合能源将成为中国能源转型和消费升级过程中最重要的一环。

虽然综合能源系统相比单独设计、割裂运行的传统单一能源系统(如电力系统、热力系统、天然气系统)更加灵活高效[6]，但是IES能否发挥其自身优势，实现经济、能效、环保的有效统一，依赖于系统的配置是否合理、运行方式是否高效。这其中，综合能源系统的优化配置[7-8]无疑是决定整个系统能效水平的重要基础。综合能源系统优化配置是指根据待规划区域内的资源禀赋情况，并结合冷热电负荷预测结果，对系统待安装的各类设备进行选型、容量和出力优化，在满足负荷需求的前提下获得最佳的设备配置和投资建议[9-10]。目前，应用于综合能源系统规划的方法主要包括三种：经验公式法、迭代搜索法以及数学优化法。

经验公式法是指设计人员根据园区负荷的构成及分类特点，从设备库中选取相关设备，并经过简单的容量和裕度计算，形成2～3套设计方案，最终通过比对遴选出技术和经济效益最佳的规划方案。经验公式法是现行最常使用的方法，但是该方法与设计人员的经验有关，其技术方案的最优性难以有效保证。迭代搜索法[11-12]是一种基于预先规则集的计算机枚举法。该方法将运行人员的设计经验提炼为具体的判断规则，并将其转化为相应的计算机语言，从而实现IES规划方案的自动匹配和生成。由于迭代搜索法的基础仍是设计人员的经验，因此该方法未能解决经验公式法的不足。有别于上述两种方法，数学优化法[13-15]基于严格的数学优化理论，对各类设备的技术机理和运行特性进行精确建模，并采用混合整数规划算法进行求解，在获得系统最佳配置方案的同时能够得到更为详细的设备输入和输出结果。数学优化法的优势在于其技术模型精准，优化结果可靠，更为重要的是它避免了规划方案的人为主观选择，使系统的结构更加合理，运行更为高效。正是凭借上述优点，数学规划法正逐步取代其他两种方法成为设计和研究人员关注的焦点。

现提出含储能装置的园区型综合能源系统的三级协同优化设计方法，其特点在于：将综合能源系统的设备选型、容量配置和运行优化三个阶段进行联合考虑统一建模，并采用系统级的构造方法对各类设备的选型和运行约束进行归纳和提炼，从而形成了结构简洁、约束紧凑的综合能源系统混合整数规划模型。针对该模型存在非线性函数项而难以直接求解的不足，通过引入辅助变量和约束实现模型的等价线性转化。

1 综合能源系统优化配置

1.1 三级协同设计方法

提出了园区型综合能源系统的三级协同优化设计方法，其主要思路是将系统的设计过程划分为设备选型、容量配置以及运行优化三个阶段，然后根据各阶段之间的递进关系，采用混合整数规划方法进行统一建模和联合求解，最终实现系统结构、离散设备台数和容量以及运行规律的同步优化。下面以某综合能源系统为例，对本文方法进行介绍。

图1(a)为某待建综合能源系统的配置结构。图中矩形为备选设备。分析图1可知，对一个综合能源系统，其能量传递过程可概括为三个环节：能源输入、能源转化以及能量输出。在系统结构确定之前，各环节存在多种备选方案或设备。不同的设计方案将导致系统的投资和运行成本产生巨大差异。为此，采用三级协同规划方法进行统一设计，其原理如图1(b)～图1(d)所示。其中，图1(b)为设备选型阶段，代表系统从设备库中选取设备的类别与型号。当型号确定之后，需要计算每类设备的台数或容量，即容量配置阶段，该阶段如图1(c)所示，图中方框内的数字代表设备的安装台数(离散设备)或最大允许安装容量(连续设备)的百分比。最后，将设备型号和台数作为输入，以满足冷、热、电负荷为约束条件，对系统的运行优化策略进行求解，以确保规划方案的整体最优性，该阶段如图1(d)所示。将三个阶段统一考虑联合优化即为所提出的三级协同优化设计方法。

图1 综合能源系统配置方法Fig.1 Configuration of integrated energy system

1.2 IES优化配置模型

根据上述设计方法，以一个简单的系统为例对IES优化配置模型进行阐述。该系统的结构如图2所示。当设备类型、台数以及容量确定时，整个系统的结构也将确定。

xij为第i类第j型号设备输入；yij为对应输出；xi、yi分别为第i类设备总输入和总输出功率；Y为负荷需求，具体可细分为电负荷、冷负荷以及热负荷等图2 简单系统示意图Fig.2 Structure of simple energy supply system

1.2.1 设备选型约束

假设第i类设备有Ji种型号可供选择(例如燃气轮机为一类设备，其包含有多个产品型号)，每类设备是否安装由0-1变量γij表示。那么对于图2所示系统，其设备选型约束为

γij∈{0,1}

(1)

若每类设备只允许选取一种型号，则有

(2)

1.2.2 容量配置约束

(3)

式(3)中：nij为第i类第j型号的设备的安装台数。

式(3)为离散设备的配置约束。对于安装容量为连续的设备，如储能装置、光伏组件等，其容量约束为

(4)

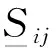
1.2.3 设备运行约束

在规划阶段，一般认为设备的输出和输入之间近似服从线性关系。当同一型号设备有多台同时在运行时，可认为各台设备的负载率相等。设备运行约束为

(5)

(6)

(7)

式(5)为设备输入输出特性约束。它表示第i类j型设备被选中(γij=1)且有δi(t)台同时在运行，每台平均输入功率为xi(t)/δi(t)，那么总输出功率为yi(t)=∑[aijγijxi(t)/δi(t)+bijγij]δi(t)，即式(5)。式(6)为输入功率限值约束，式(7)为设备最大运行台数约束。

以上约束均为离散设备的运行约束，对于储能类设备，如储电、蓄冷和储热装置，其运行约束可表示为

(8)

(9)

(10)

(11)

0.2sij≤Eij(t)≤sij

(12)

Eij(t+1)=Eij(t)(1-ηij)+

(13)

Eij(0)=Eij(T)=μijsij

(14)

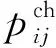
式(8)、式(9)为充放功率限值约束，式(10)、式(11)为充放功率总和约束；式(12)为蓄存容量限值约束，式(13)为容量平衡约束，式(14)为初始和终止时段容量约束。

1.2.4 系统能流平衡约束

除满足式(1)～式(14)外，在任意时段，系统均应满足如下供需平衡关系，包括电平衡、热平衡以及冷平衡等，即

(15)

1.2.5 目标函数

目标函数取年总费用最小，总费用包括年运行费用和初投资折算为每年的平均费用，计算公式为

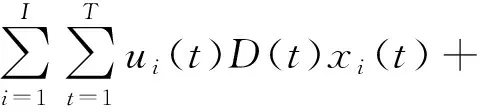
(16)

式(16)中：等式右侧第一项为能源消耗支出，第二项为投资年等值费用；ui(t)为电能或天然气的价格；D(t)为典型时段t在全年的持续时间；R为投资回收系数，其值由年利率r和设备使用寿命τ决定，计算公式为R=r(1+r)τ/[(1+r)τ-1]；cij为第i类第j种型号设备单位购置成本；cst为储能装置单位容量的购置成本。

1.3 整数线性求解方法

式(1)～式(16)即为综合能源系统的最优配置模型。可见，该模型对各类设备的选型与运行约束做了精炼的归纳和描述，相较于以往按单个设备建模的方式更为简洁和紧凑，同时也大幅提高了程序编写的可复用性。

由于该模型中含有乘积运算[式(5)]，即γijxi(t)和γijδi(t)，因此它是一个典型的混合整数非线性规划问题。对于这类问题，以现有的技术难以做到直接快速求解。鉴于此，通过引入辅助变量和约束对该问题进行了等价转换，将其转变为易于求解的混合整数线性规划问题。

首先，引入连续变量ξij(t)和ζij(t)，分别代替式(5)中的非线性乘积项γijxi(t)和γijδi(t)，即有

(17)

然后，增加如下线性约束，以保证转换前后的约束具有等价性，即

(18)

(19)

由式(18)可知，当γij=0时，有ξij(t)=ζij(t)=0；当γij=1时，有ξij(t)=xi(t)和ζij(t)=δi(k)成立，因此式(18)与式(17)等价。至此，原非线性混合整数规划问题已转化为整数线性规划问题。利用分支定界算法或CPLEX、Gurobi等商用求解器即可对转化后的问题进行直接求解。

2 算例分析

2.1 算例说明

为验证所提规划方法的有效性，对江苏某综合能源园区三期工程进行优化配置研究。该园区位于无锡市东港镇，规划面积为7.98 km2。园区建设完成后，将为印染纺织、橡胶轮胎、装配制造等各类企业提供冷、热、电等多种能源服务。

待规划园区的能流结构如图3所示。由图3可知，系统的用能需求包括电、冷、热等，拟安装的设备有光伏(photovoltaic，PV)、燃气轮机(gas turbine，GT)、余热锅炉(heat-recovery boiler，RB)、燃气锅炉(gas boiler，GB)、电制冷机(electric cooler，EC)以及蒸汽型吸收式制冷机(absorption chiller，AC)等。其中，燃气轮机和余热锅炉采用“一拖一”的方式安装和运行，可视为一套设备，因此系统待选设备类型数为I=5。各类备选设备的技术和经济参数[15]如表1～表3所示。其中，光伏的最大可安装容量(由园区可利用面积包括屋顶、闲置土地等测算得到)为11.4 MW，其他各类设备最多可安装4台。

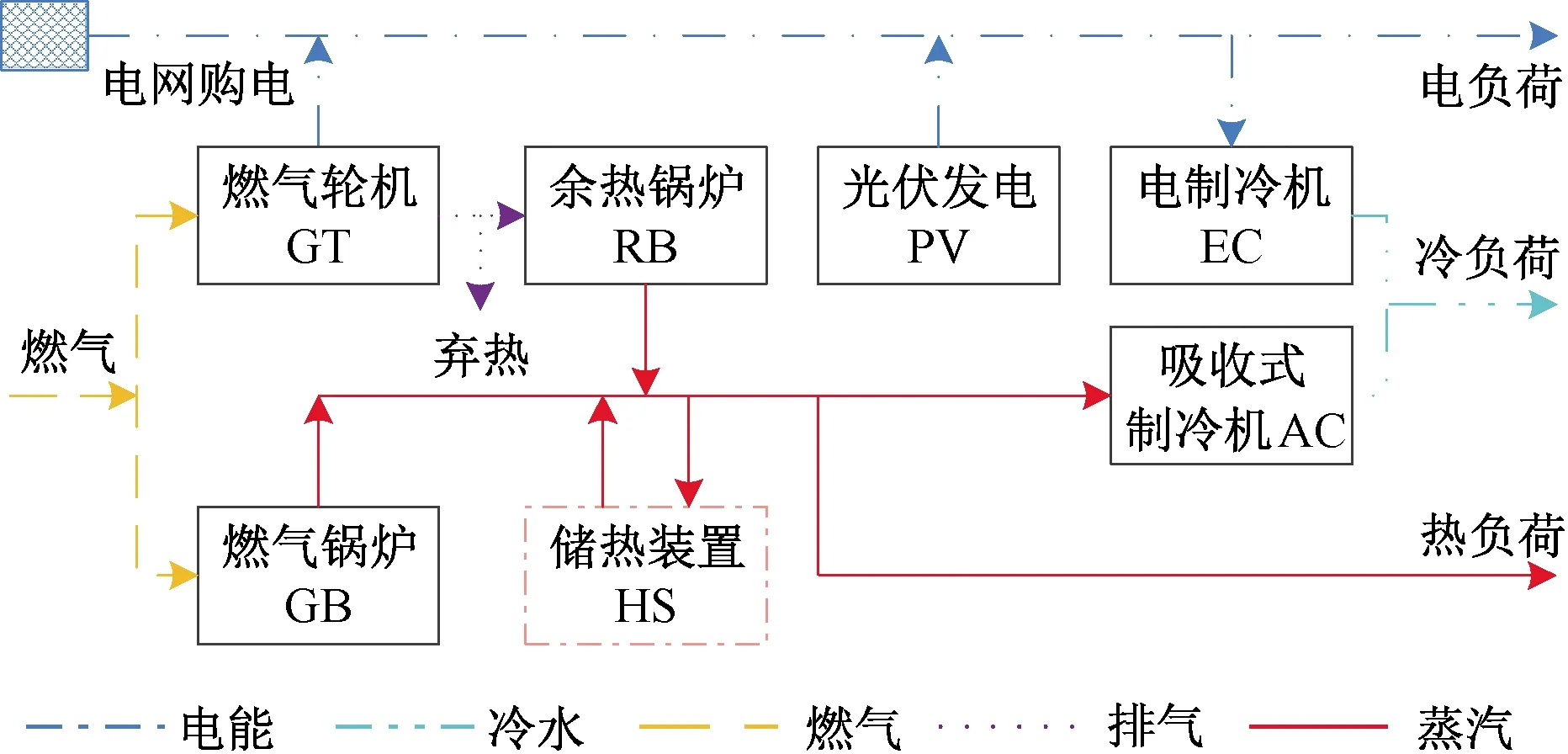
图3 待规划系统能流结构Fig.3 Energy supply structure of the system to be planned

表1 备选燃气轮机参数Table 1 Parameters of alternative gas turbines

表2 其他备选设备参数Table 2 Parameters of other alternative equipment

表3 储热装置参数Table 3 Parameters of heat storage

根据园区所在地气候变化特点，将全年划分为夏季(7—9月)、冬季(12月—次年3月)和过渡季(4—6月，10—11月)三个典型日，每个典型日用24个时段代替，全年共计72个时段。各典型日时间分别为92、121、152 d。三个典型日的光照强度分布和冷热电负荷预测结果分别如图4和图5所示，测试时间从0:00开始，其中光照强度数据取自中国气象数据中心，冷热电负荷数据则根据园区的建筑面积、蒸汽压力温度、照明面积、绿化率等基础数据参数预测得出。

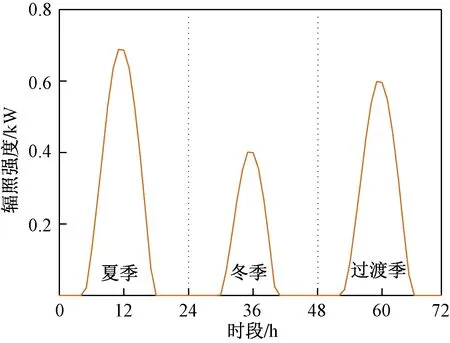
图4 各典型日光照强度Fig.4 Solar light intensity of typical days

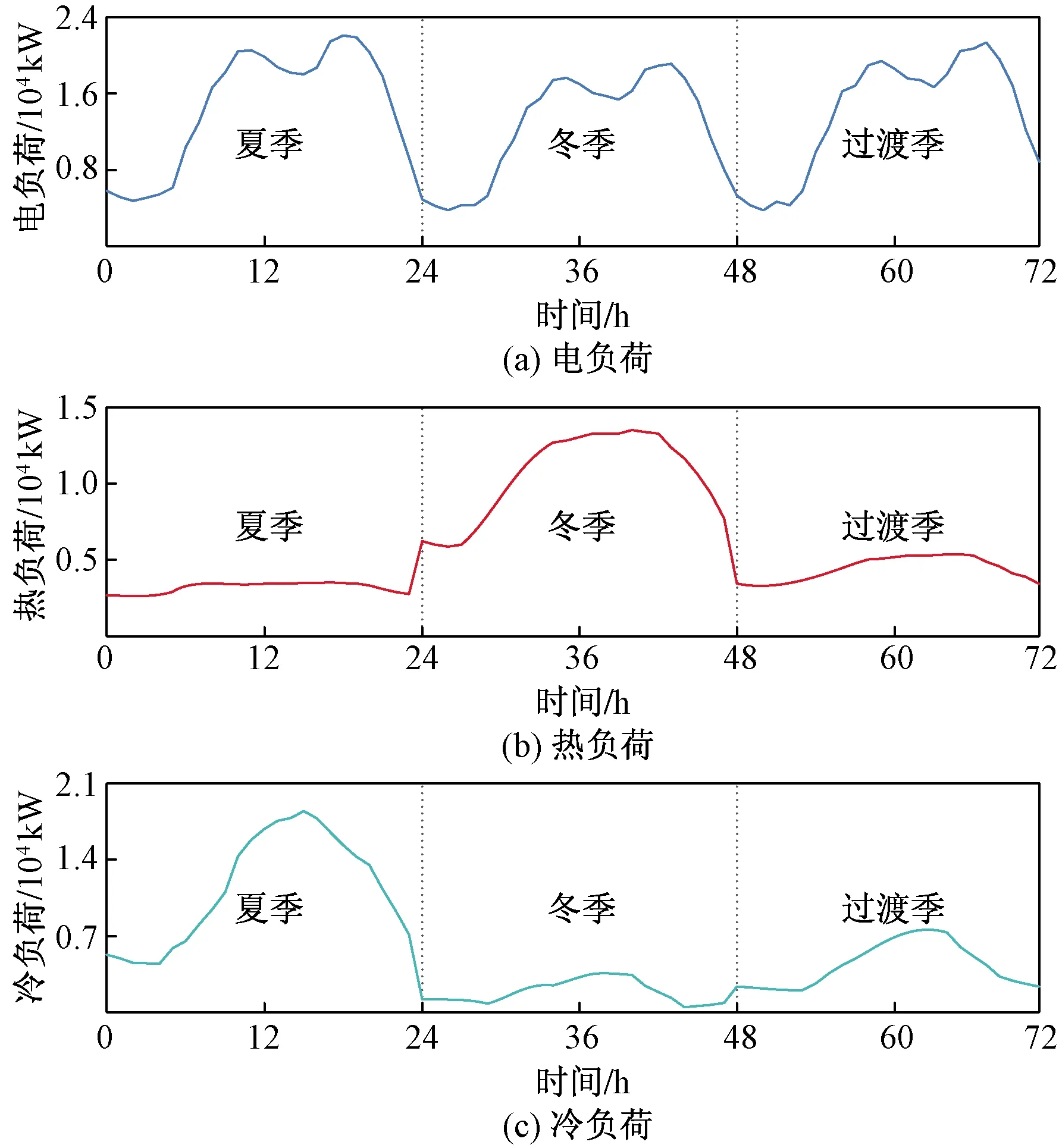
图5 各典型日负荷曲线Fig.5 Load curves of typical days

计算中使用的经济参数如下：售电电价采用江苏省发展和改革委员会发布的普通工业分时销售电价(小于1 kV)，峰谷时段划分及对应电价如表4所示。天然气价格则参考江苏省物价局自2015年起执行的非民用天然气最高门站价格2.86 元/Nm3，燃气低位热值取36 000 kJ/Nm3。融资利率为5.0%(根据中国人民银行发布的5年以上基准利率4.9%上浮得到)，设备寿命取15年。

表4 典型日分时电价Table 4 Electricity price in typical days

2.2 计算效率分析

考虑到燃气轮机存在着热电耦合，即在发电的同时必产生一定比例的热，为说明热电耦合对系统计算结果的影响，下面分燃气轮机不弃热、弃热和增加储热(heat storage，HS)装置三种情形进行讨论，具体测试方案如表5所示。

表5 储热装置参数Table 5 Parameters of heat storage

表5列出了三种情形对应的计算时间。分析表5可知，由于情形1不允许弃热，热电强耦合关系的存在增加了算法寻优的难度，导致其计算效率最低。情形2允许弃热，极大改善了问题的松弛性，因而情形2的效率要高于情形1。情形3虽然考虑了储能配置和运行约束，相比情形1问题的规模更大，但储能装置的引入减弱了系统运行的刚性，在一定程度上有效缓解了热电耦合的影响，因此其计算效率仍高于情形1。

2.2 配置结果分析

三种情形下系统的优化配置结果如表6所示。可以看到，三种情形的光伏均以最大安装容量进行配置，这是因为光伏一经安装后其运维成本很小，同时能产生大量电力。情形1和情形2的配置结果完全相同，说明燃气轮机是否弃热对设备配置的影响有限。情形3与情形1相比，增加了35.85 MW·h的储热和1台5.58 MW的电制冷机，同时减少了一台7.86 MW的燃气锅炉和5.18 MW的吸收式制冷机容量。这表明引入储热装置可以有效减少热能生产和转化设备的安装容量。

表6 不同情形下的优化配置结果Table 6 Optimal configuration under different cases

三种情形下的系统投资和运行费用如表7所示。由表7可知，在经济上，情形1、2、3的年总费用依次降低。对比情形1和情形2，在系统配置相同的情况下，考虑弃热的系统运行方式反而比不弃热更为经济。这是因为弃热的运行方式更为灵活，可以在电价高峰时段，充分发挥燃气轮机在发电上的低成本优势，而不用受热电耦合的影响被迫压低电负荷输出。虽然情形3与情形1、2相比，投资有所增加，但总费用在三者之中最低，这是因为储热装置的引入可以进一步提高系统运行的灵活性，在满足冷热电负荷需求的同时，利用峰谷电价差获得更大的经济效益。在能耗方面，情形2由于弃热导致其总能耗(天然气和购电)最大，情形1次之。相比之下，情形3多安装一台能效比为5.04的电制冷机，同时免去了燃气锅炉的安装和使用，因此其总能耗最小。

表7 不同情形下的费用和能耗Table 7 Costs and energy usage under different cases

2.3 运行结果分析

情形1夏季典型日条件下各类设备的运行优化策略如图6所示。可以看到，各时段冷、热、电平衡均能得到满足。在电价高峰时段(表3)，系统电负荷尽量由光伏和燃气轮机承担，电量不足的部分则从电网购电来补充。此时，燃气轮机(#5)每发1度(1 kW·h)电将产生1.702 6 kW·h的热，发电成本为1/0.306×3 600/36 000×2.86=0.934 6元/(kW·h)，低于电网电价，因此燃气轮机应开机运行并尽量满发，以降低购电成本。考虑到情形1不允许弃热，为满足热平衡，燃气轮机被迫压低负荷输出，即处于不满发状态。在平时段，燃气轮机产生1 kW·h的热，需消耗0.191 9 Nm3天然气，同时产生0.587 3 kW·h的电，折合制热成本为0.154 6 元/(kW·h)。当考虑吸收式制冷机(#3)的能效比时，燃气轮机-吸收式制冷机的制冷成本为0.124 6 元/(kW·h)；相比之下，燃气锅炉的制热成本为0.312 2 元/(kW·h)，电制冷机(#4)的制冷成本为1/5.04×0.671 5=0.133 2 元/(kW·h)，因此在平时段，优先由燃气轮机-吸收式制冷机提供冷热电负荷需求，冷负荷不足部分再由电制冷机补充。在电价低谷时段，即0：00—8:00，燃气轮机发电和制热将不具备价格优势，此时系统应尽量从电网购电，燃气轮机则处于停机状态。系统热负荷和冷负荷分别由燃气锅炉和电制冷机满足。

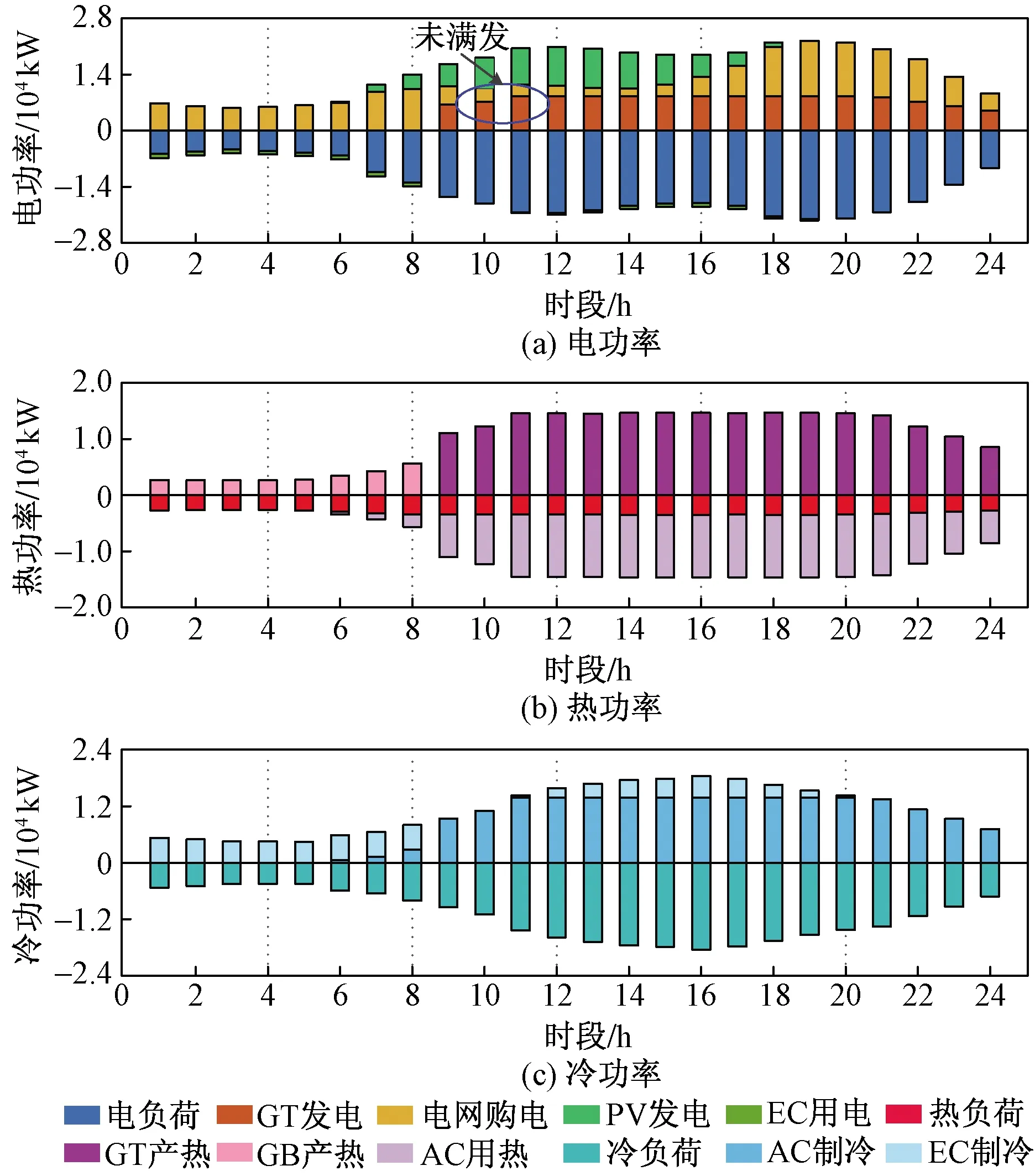
图6 情形1运行优化策略Fig.6 Optimal operation strategies under case 1

情形2冬季典型日的运行优化结果如图7所示。相比于情形1，在电价高峰时段，情形2允许弃热。因此当吸收式制冷机容量不足或冷、热负荷需求不够时，燃气轮机仍可以充分利用发电容量，争取满发电，多余的热量则直接舍弃，这一现象解释了表7中有关情形2购电成本最小、燃气成本以及能耗最大的原因。在电价平时段，若燃气轮机大量弃热，系统运行则不经济，因此该阶段没有弃热现象产生。与情形1相似，在电价低谷时段，主要由燃气锅炉和电制冷机供应冷热负荷。具体地，燃气锅炉优先满足低谷时段的热负荷需求[制热成本为0.312 2 元/(kW·h)，低于燃气轮机的制热成本0.358 8 元/(kW·h)]，电制冷机优先满足冷负荷需求[制冷成本为0.064 2 元/(kW·h)，低于“燃气锅炉-吸收式制冷机”组合的制冷成本1/1.24/0.916×3 600/36 000×2.86=0.251 8 元/(kW·h)]。

图7 情形2运行优化策略Fig.7 Optimal operation strategies under case 2

情形3过渡季典型日的运行优化策略如图8所示。由图8可知，在电价高峰时段，情形3没有弃热现象产生，多余的热量则直接通过储热装置存储起来，并在电价平时段和谷时段放出(图8中储热容量曲线)。正是由于上述原因，系统减少了燃气锅炉和吸收式制冷机的安装容量，同时其总能耗在三者之中最小。与情形2一致，情形3中的燃气轮机在电价高峰时段满发，在低谷时段停机。所不同的是，情形3中的燃气轮机在平时段尽量少发电和制热，这是因为储热装置的放热成本几乎为0，而此时燃气轮机发电成本高于购电电价，系统优先使用储热装置蓄存的热量，不足的部分再由燃气轮机承担。