基于自适应周期扰动观测器的变频压缩机转速波动抑制

孟凡琨 文小琴 游林儒

(华南理工大学 自动化科学与工程学院，广东 广州 510640)

永磁同步电机具有结构简单、功率密度高、调速范围广等特点，在变频压缩机(制冷行业)中具有广泛的应用。变频压缩机的转子可以分为3种形式：往复式、旋转式(单转子和双转子)、涡旋式。单转子变频压缩机在能效、成本和性价比方面具有一定的优势，因而具有较大的市场份额。由于偏心曲轴和滑块将气缸分为左右容积，变频压缩机通过转子驱动偏心曲轴周期性地实现冷媒吸入、压缩和排出，近似周期的负载导致转速存在波动，且频率越低，转速波动越为明显。随着转速控制精度的提高，变频压缩机低频范围转速波动以及潜在的失步等问题突显出来。为了减小变频压缩机低频运行时的转速波动，国内外学者展开了广泛的研究并取得一定成果。当前，工程中普遍采用正弦波力矩补偿，该方法忽略周期性负载扰动的谐波分量，因而负载扰动未能得到有效补偿，低频时转速波动较为显著。黄辉等[1]采用负载转矩自动补偿器进行电流补偿，该方法忽略了高频转矩分量对转速波动的影响，同时，转矩自动补偿器中的低通滤波器将产生相位滞后，导致转速波动抑制性能有限。张国柱[2]通过在线傅里叶分析提取转速波动的基波成分，推算抑制转速波动的电流补偿量。然而，该方法忽略了转速的谐波成分，此外，电流补偿量的推算过程关系较为复杂，产生的相位滞后一定程度上降低转速环带宽。文献[3]采用比例谐振控制器(PR)抑制负载转矩扰动，通过离线傅里叶分析得知谐振频率为转子机械角频率的固定倍数，该方法的自适应性较差，当工况发生变化时，谐振频率的偏差将导致速度波动抑制效果变差。

重复控制通过构建适当的内模，可以有效地实现周期信号的抑制或跟踪[9]。由于其结构简单且易于实现等特点，重复控制器在永磁同步电机控制中得到了广泛的应用[10]。文献[11]采用低通滤波器提高重复控制器的鲁棒性，但高频段幅值波动和相位滞后较为显著，降低了扰动抑制性能。文献[12]采用相位超前环节对重复控制器引起的相位滞后进行补偿，不同的频段采用不同的相位补偿函数，使得相位具有一定的稳定裕度，但该方法较为繁琐。文献[13]采用基于拉格朗日(Lagrange)级数展开式对非整数延时进行逼近。与普通的重复控制相比，理论上，当采样频率一定时，基于Lagrange级数展开式的重复控制器可以抑制任意频率扰动，但因灵敏度与计算复杂度的相互影响，需综合考虑重复控制器的控制精度以及动态响应。

为了解决上述问题，本研究采用自适应周期扰动观测器(APDOB)实现周期性负载扰动观测，并对电流进行补偿，以减弱周期性负载扰动对变频压缩机转速的影响。本研究构建周期负载扰动观测器并对参数进行分析与设计；然后构建自适应陷波器估计周期扰动基波频率；最后通过仿真和实验验证了所提方法的可行性与有效性。

1 变频压缩机模型

为了简化变频压缩机的动力学模型，假设：①忽略铁心饱和；②不计涡流及磁滞损耗；③三相电流产生的磁通以及转子磁通呈正弦分布。在同步旋转坐标系下，其运动方程为：

(1)

其中,id和iq分别为坐标系下定子电流分量，Ld和Lq分别为dq坐标系下的定子电感分量，Te为电磁转矩，Td为负载转矩，J为压缩机等效转动惯量，B为粘滞阻尼系数，ωm为转子机械转速,Bωm项通常可以忽略不计，Np为极对数，Ψm为转子永磁体磁链。

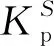
图1 变频压缩机DOB结构框图

图2示出了变频压缩机负载转矩波形(一个机械周期)[1]。可以看出，负载转矩波形随着工况的不同而变化，且负载转矩幅值和相位存在着较为明显的差异。因此，如何构建自适应扰动观测器，成为解决转速波动问题的关键。

系统控制目标要求降低变频压缩机低频范围的转速波动，使得转速偏差尽可能地小。为此，做以下假设：

图2 不同工况下负载转矩曲线

(1)在相同的工况下，负载转矩扰动具有近似的周期性和重复性。

(2)测量噪声主要存在于高频范围内，低通滤波器可以有效地抑制测量噪声。

(3)在相同的工况下，转子转速具有相似的周期性和重复性。

假设负载扰动d(t)满足如下微分方程，即

(2)

(3)

式中，s为拉普拉斯算子，d(0,s)为扰动信号d(t)的初始状态，由各阶状态初始值决定。假设负载扰动d(t)为周期信号，则其离散形式可表示为

d(k)=d(k-N)+f(k)

(4)

其中，

(5)

d0(k)和N分别为扰动信号d(t)的初始状态和周期延时，k为采样序列。由z变换可得

(6)

1.1 普通的扰动观测器分析

图3为普通扰动观测器结构框图。其中，r、y、d、n、、P、Pn、e、u和δ分别为控制系统输入、输出、等效扰动、测量噪声、扰动观测值、对象实际模型、对象标称模型、跟踪误差、补偿后控制量以及模型误差。C(z-1)为系统固有的控制器，如比例积分微分控制(PID)或H无穷控制(H∞)，用于实现伺服或鲁棒特性；Q(z-1)为待设计的滤波器；m为Pn的相对阶次。假设模型偏差由乘性偏差构成，即

图3 普通DOB结构框图

P(z-1)=(1+δ(z-1))Pn(z-1)

(7)

如图3所示，为了简便，省略离散域延迟因子z-1，可得控制系统的灵敏度函数:

(8)

图4为基于小增益定理的扰动观测器结构框图，当满足小增益定理时，控制系统鲁棒稳定。

图4 基于小增益定理的DOB结构框图

1.2 Q滤波器参数设计

假设扰动为周期信号且满足相应的内模，由内模原理可知，如果灵敏度函数S(z-1)包含内模1-z-N，则扰动d至误差e的传递函数Ged=S(z-1)P(z-1)将渐进趋近于零。令

1-Q(z-1)z-m=1-z-N

(9)

当Q(z-1)采用有限脉冲响应(FIR)滤波器时，即Q(z-1)=z-(N-m)。为增强滤波器的鲁棒性，本研究采用无限脉冲响应(IIR)滤波器[10]，即

Q(z-1)=BQ/AQ，令：AQ=1-αNz-N，则BQ=(1-αN)z-N+m,即

(10)

图5 Q滤波器关于q(ejωTs)的增益

1.2.1 扰动信号周期N的设计

(11)

证明过程如下[15]：定义周期扰动d(t)的延时N为

(12)

其中，σ为非整数且0<σ<1。由于扰动信号的基波频频ω0满足式(9)，因此，将N值带入可得

(13)

由于0<α<1，通常N取较大值，存在αN≈0。则通过级数展开可得

1.2.2 参数α的设计

参数α为IIR滤波器零点与极点的比值且α∈[0，1]。由式(10)可知，当α=0时，Q(z-1)为FIR滤波器，即Q(z-1)=z-N+m；当α=1时，则完全阻断了周期扰动补偿。为了简化分析，令q(z-1)=1,1-Q(z-1)z-m和Q(z-1)z-m关于α的幅值曲线如图6所示。相关参数分别为ω0=500 rad/s，Ts=0.1 ms和m=1。可以看出，随着α的增加，1-Q(z-1)z-m幅值呈现梳状结构；在特定频率(如：500、1 000、1 500 rad/s等)下，Q(z-1)z-m幅值保持不变，其余频率范围幅值具有较为显著的衰减。因此，Q(z-1)z-m能够较好地滤除周期成分。特别地，当α=0时，Q(z-1)z-m幅值恒等于1，此时，扰动d的周期成分以及非周期成分直接用于反馈补偿，同时，1-Q(z-1)z-m的最大值‖1-Q(z-1)z-m‖∞=2，也就是说，相应频率扰动幅值增益将放大100%。

图6 α与Q滤波器

1.2.3 截止频率ωc设计

截止频率ωc的设计综合考虑扰动抑制性能以及鲁棒稳定性[16]。为了简化分析，忽略z-m对截止频率的影响。首先，假定扰动信号基波频率为ω0时，则Q滤波器增益为

令к=ω0/ωc，可得Q滤波器幅值与к的关系曲线，如图7所示。可以看出，对于给定的基波频率ω0，截止频率ωc的下限由增益曲线的上限决定。

图7 κ与Q滤波器增益

基于以上设计，截止频率ωc的上限由PDOB鲁棒稳定性得出。由图4小增益定理等效模型[10]可知，如果δ(z-1)稳定且满足H∞范数有界，且

(14)

则控制系统鲁棒稳定。其中，

(15)

2 自适应周期扰动观测器

2.1 扰动基波频率估计

当周期扰动基波频率发生变化时，扰动抑制性能也随之发生改变[17- 18]。因此，基波频率估计为自适应周期扰动观测器的核心部分，本研究采用基于Steiglitz-McBride(S-M)方法的自适应陷波器(ANF)实现扰动基波频率估计。图8为自适应周期扰动观测器的结构框图，其中，A(z-1)=1+αz-1+z-2(α=-2cos (ωTs))，ρ为陷波参数。基于S-M方法的自适应陷波器频率估计算法如下所示[19- 20]。

图8 APDOB结构框图

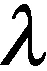
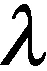
ρ=0.8，ρr=0.99，ρ∞=0.995,

主循环：

ψ(n)=-ρg(n-Δ)+(ρ-1)h(n),

e(n)=g(n-Δ+1)+ρ2g(n-1-Δ)-

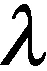
频率估计值：

2.2 相关参数设计

延迟参数Δ，带通滤波器带宽bp和低通滤波器截止频率影响基波频率ga估计。为了优化相关参数设计，选择频率参考值为

(16)

图9 Δ与频率估计

(17)

图10 bp与BPF增益

低通滤波器qa(e-jωTs)=ga/(jω+ga)，ga为截止频率，用于平滑参数估计，防止暂态超调或失调。如图11所示，当ga=50时，初始时刻频率估计存在较大暂态超调；当ga=10时，暂态超调得到有效的抑制。因此，适当的截止频率可以抑制频率估计过程中的暂态超调或失调。

3 仿真和实验

3.1 仿真

上述所提自适应周期扰动观测器的核心为扰动信号基波频率估计。为了验证该算法的可行性，基于Matlab/Simulink搭建普通DOB和APDOB数值仿真模型，相关参数如表1所示。

图11 ga与频率估计

表1 仿真参数

仿真模型如式(18)所示，其中，D(z-1)为伪微分算子，周期扰动dp由基波信号与相应的谐波构成。

(18)

其中，基波频率参考值为：

(19)

图12为APDOB基波频率估计曲线。其中，初始频率设定为 2 Hz。可以看出，初始时刻频率保持恒定，原因在于中心频率偏差使得BPF无法有效滤除正弦信号，依然选择2 Hz为频率估计值。当频率发生突变时，基于S-M方法的自适应陷波器可以在5 s之内实现频率准确估计(偏差小于0.1 Hz)，同时，暂态过程平稳且无明显的超调。因此，基于S-M方法的自适应陷波器频率估计可以确保周期扰动的抑制性能。

图12 APDOB基波频率估计

图13为指令信号跟踪误差曲线。其中，指令信号给定值为 0，用于直观地体现周期扰动抑制性能。可以看出，当基波频率变化前，有限的灵敏度增益使得DOB具有较大的跟踪误差，当基波频率变化后，由于具有良好的频率自适应功能和较高的灵敏度增益，APDOB能够减弱周期扰动对跟踪信号的影响；然而，对于普通DOB，截止频率范围之内的所有谐波分量用于扰动补偿，跟踪误差幅值减小且形状与频率变化之前保持一致。

图13 指令信号跟踪误差

3.2 实验

为了验证所提算法的有效性，搭建变频压缩机实验平台，并与比例积分控制(PI)(无电流补偿)和 DOB 进行对比分析，其控制系统框图如图14所示。其中，采用 DSP TMS320F28069 作为主控制器，滑模观测器(SMO)用于实现角度和转速估计，载波和采样频率设定为10 kHz，实验参数如表2所示。相关数据经USB-CAN转换器发送至LABVIEW上位机并进行数据处理。当变频压缩机运行于15 Hz时，其q轴电流波形如图15(a)-15(c)所示。可以看出，当采用 PI 控制器时(无电流补偿)，近似周期性的负载扰动使得q轴电流呈现周期性且幅值波动较为明显，进而导致SMO产生一定的周期性偏差。当采用普通 DOB 时，q轴电流得到一定程度的补偿，原因在于：①普通 DOB 可以有效抑制高频扰动信号(高于截止频率)，主要包括功率模块的非线性压降导致的高次谐波和电流AD采样噪声等；②有限的灵敏度增益无法较好地抑制周期性扰动(低于截止频率)；③减小 DOB截止频率能够增加灵敏度增益，而相应的相位滞后将影响周期扰动抑制性能；当采用APDOB时，除了非周期成分之外，q轴电流得到有效的补偿。图15(d)-15(f)示出了20 Hz时q轴电流波形(近似相同的工况下)。可以看出：当采用PI控制器时(无电流补偿)，周期性扰动导致q轴电流产生较为明显的波动，且形状与15 Hz保持一致；当采用APDOB时，除了一些非周期成分，q轴电流得到有效的补偿。

图14 变频压缩机控制框图

表2 实验参数

图16(a)-16(c)为变频压缩机15 Hz时相应的转速曲线。当采用PI控制器时(无电流补偿)，转速波动呈现周期性且具有明显的偏差；当采用普通 DOB时，有限的灵敏度增益使得转速呈现较小的周期性偏差；当采用APDOB时，周期性扰动得到有效的抑制，转速平稳且具有较小的偏差。为了直观体现转速波动抑制性能，采用均方根误差(RMSE)作为转速波动率的评价指标，即

图15 15 Hz和20 Hz q轴电流波形

(20)

其中：ωref为参考转速；M=Npfspd/f，为采样次数；f为运行频率；fspd=1 kHz，为速度环采样频率。当变频压缩机运行于15 Hz时，参考转速为300 r/min，当采用PI控制器(无电流补偿)、普通DOB和APDOB时，相应的转速波动率分别为5.8%、1.5%和0.6%；当运行于20 Hz时，参考转速为400 r/min，转速波动率分别为4.5%、1.3%和0.4%。可以看出，与普通的DOB相比，较高的灵敏度增益以及频率自适应使得APDOB能够有效地减小周期性扰动导致的转速偏差。此外，在近似相同的工况下，转速波动率随着频率的降低而升高，而相对较高的参考转速使得转速波动率降低。因此，转速波动抑制主要适用于低频范围。

图16 15 Hz和20 Hz 转速波形

4 结语

针对变频压缩机普遍存在的低频转速波动问题，本研究通过构建自适应周期扰动观测器实现扰动估计与电流补偿。首先，构建周期扰动观测器并进行相关参数分析；其次，采用基于S-M方法的自适应陷波器估计扰动基波频率；最后，在变频压缩机实验平台进行分析验证，分别运行于15 Hz和20 Hz。结果表明：与普通DOB相比，APDOB能够有效地抑制变频压缩机低频范围的转速波动。因此，该方法为变频压缩机实现低速高效运行提供一个有效的途径，具有节能降耗的实际意义。