轮对的轴向窜动对U2000型数控不落轮车床直径测量值的影响

孙德鹏

（奈斯赫贸易（北京）有限公司，北京 100048）

0 引言

轴承是铁路及轨道交通用车转向架的重要零部件，承受着车辆大部分的自重。列车行驶时，钢轨对轮对径向、轴向的冲击力以及机车牵引力所产生的附加载荷等都会对轴承产生冲击。轴承组装后必须检查并保证组装状态左右转动的灵活性。轴承的轴向窜动量应该符合规定，大的窜动量会导致轴承旋转精度降低、使用寿命缩短以及车辆高速运行或过弯道时易发生卡死等故障。另外，当出现严重横向减振器漏油、导柱摩擦套磨损、牵引拉杆松动、轮对磨耗以及剥离等现象，运行时就会产生轮对窜动和转向架摆动[1-2]。

U2000型数控不落轮车床是德国Hegenscheidt-MFD公司生产的高性能数控车床。轮对窜动会影响车床的测量，对镟修作业的指标影响较大。由于车辆轮对窜动量、窜动形式以及关联部件实验的模拟难度大，因此结合列车日常管理和镟修的安全性考虑，采用系统动力学仿真平台来研究轮对轴向窜动对车床测量值的影响，这是解决问题最快的途径，也是最好的方法。

该文采用多体动力学仿真平台RecurDyn，根据轮对和直径测量轮旋转周长相等的关系，进行了对无窜动、单项窜动以及往复窜动3种工况的仿真，并得出不同工况的窜动量对车床直径测量值准确性以及加工精度的影响，仿真结果为镟修时轮对直径的测量补偿提供了理论参考。

1 模型的建立

1.1 U2000型数控不落轮车床直径测量原理

测量直径时，轮对不断旋转，光栅计数装置记录被加工轮对的旋转圈数；直径测量轮紧靠被加工轮对踏面，内部编码器记录直径测量轮旋转圈数。由于直径测量轮的直径是定值，且两轮旋转的周长相等，因此可以得出轮对的直径，其表达式如公式（1）所示。

式中：n1为轮对旋转的圈数；d1为轮对直径；n2为直径测量轮旋转的圈数；d2为直径测量轮的直径。

1.2 三维实体模型的建立

轮对和钢轨接触，其表面的形状需要符合规定。为了使轮对在钢轨上平稳运行，顺利通过曲线，降低车轮磨耗，延长镟修公里数，踏面应该具有合理的外形。踏面有锥形（1∶20）和磨耗形2种。中国铁路自20世纪70年代后期开始试验磨耗形踏面；至80年代中期，机车、车辆先后制定了1种磨耗形的标准踏面。该文选用最常用的铁标LM32磨耗形踏面，阐述轮对轴向窜动对车床直径测量值的影响，踏面尺寸如图1所示。

根据图1的曲线，在AutoCAD中画出LM32磨耗形车轮的踏面轮廓曲线，坐标原点设立在图1中的踏面基点处。把组成轮廓曲线的各线段首尾端点的坐标记录下来，在UG中通过点命令生成样条曲线，借助扫掠等命令完成对轮对和车床直径测量轮的建模。

2 驱动Step函数定义

将建立好的实体模型转化为Parasolid格式，并在导入的Recurdyn软件建立动力学模型。由于轮对在转动过程中会产生轴向窜动，因此对轮对的轴向定义驱动。在Recurdyn中可以利用Step函数，其定义如公式（2）所示。

式中：x为自变量，可以是时间的任意函数；x0为自变量的step函数的起始值，可以是常数、函数表达式或设计变量；x1为自变量的step函数结束值，可以是常数、函数表达式或设计变量；h0为函数step的初始值，可以是常数、设计变量或其他函数表达式；h1为step函数的最终值，可以是常数、设计变量或其他函数表达式。

3 仿真结果及分析

仿真模型如图2所示，确定导入Recurdyn 中模型的材料属性，然后对其定义约束条件、运动副以及施加受力等。在轮对和ground之间添加转动副，转动驱动为360 °/s，移动驱动为Step函数。模拟轴向窜动量下的工况，在直径测量轮和ground之间沿X方向添加移动副和弹簧阻尼，弹簧阻尼模拟实际情况下测量轮上升的液压缸，该液压缸让直径测量轮紧贴轮对旋转，在直径测量轮和轮对之间添加接触。

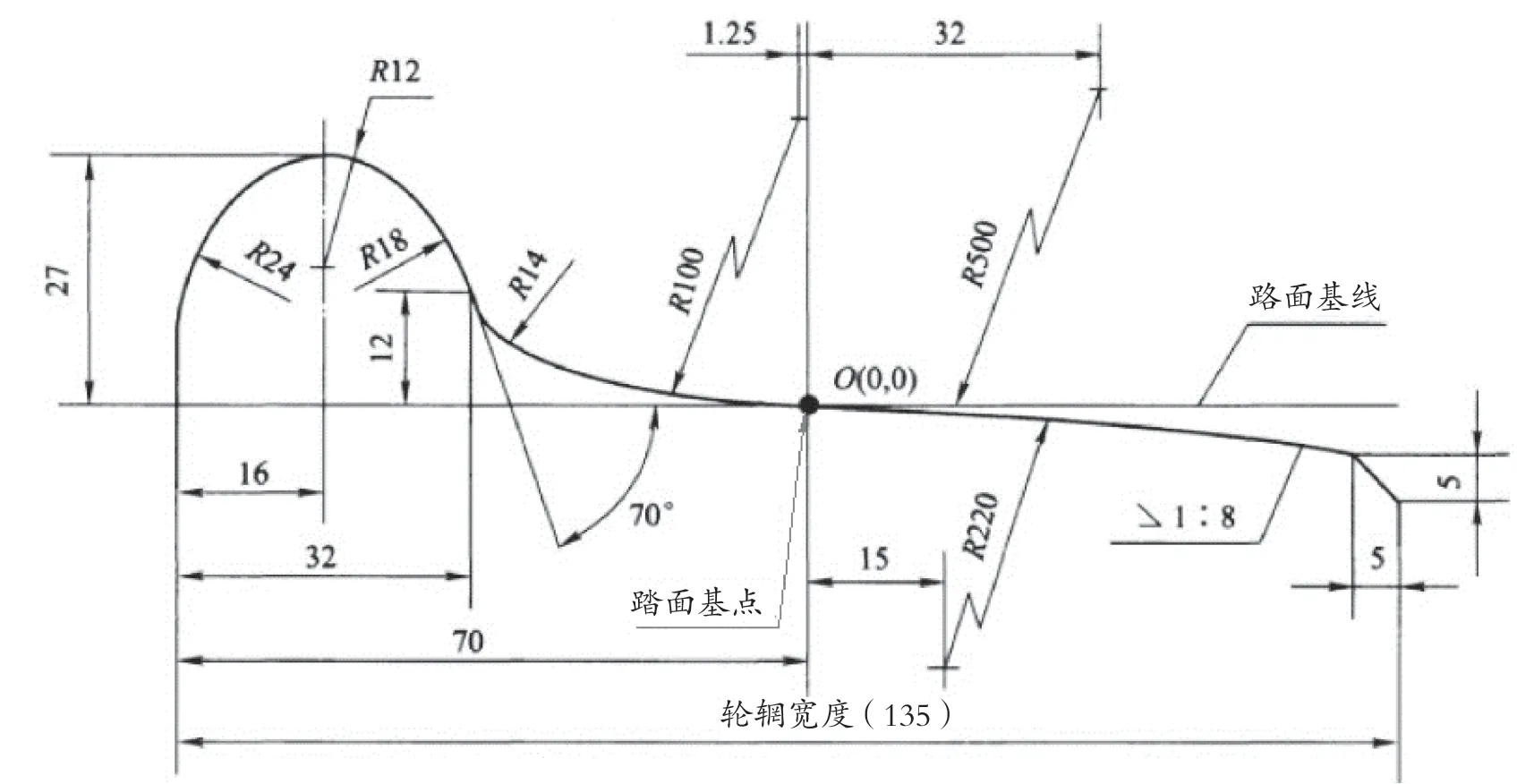
图1 LM32磨耗型踏面（尺寸单位/mm）

图2 动力学仿真模型

建模时的尺寸、物理参数和接触参数见表1。

表1 模型尺寸、物理参数和接触参数

3.1 无窜动仿真分析

无窜动轴向位移控制函数的值为0，轮对转速为360 °/s，仿真时间为1 s，步长为100，输出时间段为0 s～1 s，仿真结果如图3所示。从图3中可以看出，当轮对转动1圈，即360 °，直径测量轮旋转为3780.210 °，根据公式（1）可得新的表达式，如公式（3）所示。

仿真得出轮对的直径为840.047 mm，轮对实际的直径为840 mm，误差为0.047 mm，与实际用LM32新轮对在数控不落轮车床上测量的误差波动范围基本相符，同时验证了选取仿真模型的约束、驱动、力以及接触等参数的正确性，为下面窜动的仿真提供了基础。

3.2 单项窜动仿真分析

设置单项窜动轴向位移控制函数为step（time，0，0，0.25，x）+step（time，0.25，x，0.5，-x）+step（time，0.5，-x，0.75，x）+step（time，0.75，x，1，0），x分别为0.3 mm、0.6 mm和0.8 mm，轮对转速为360 °/s，仿真时间为1 s，步长为100，输出时间段为0 s～1 s，仿真结果如图4所示。由于直径测量轮在0 s～1 s的仿真时间中转动的度数曲线斜率相差很小，因此4条曲线对比时，时间轴选取0.998 s～1.000 s。

由表2可以看出，当单项窜动为0.3 mm时，测量的轮对直径值的误差已经达到1.309 mm；当单项窜动超过0.6 mm时，直径误差就会加速增加；当单项窜动为0.8 mm时，误差已经达到2.469 mm。当单项窜动量过大时，就会导致粗车结束后，同轴轮径差依然很大，一旦超过精车的切削深度，机床将会报警，这时需要返回加工前测量，让机床再次生成加工建议，或者只能进行不带测量的深切加工，这就会影响加工的效率。

表2 单项窜动对直径测量值的影响

图3 直径测量轮转动角度曲线

图4 不同单项窜动量时直径测量轮转动角度曲线

3.3 往复窜动仿真分析

设置往复窜动轴向位移控制函数为step（time，0,0,0.25，x）+step（time，0.25,x,0.5，-x）+step（time，0.5,-x,0.75，x）+step（time，0.75,x,1，0），其中x分别为0.3 mm、0.6 mm和0.8 mm，轮对转速为360 °/s，仿真时间为1 s，步长为100，输出时间段为0～1 s，仿真结果如图5所示。

图5 不同往复窜动量时直径测量轮转动角度曲线

往复窜动时，时间轴选取比单项窜动时更短，即选取0.9996 s～1.000 s。由图5可以看出，不同窜动量的直径测量轮在0 s～1 s转动的度数曲线非常接近，这说明直径测量轮转动的度数相差很小，换算出的轮对直径值相差很小，往复窜动时测量的轮对直径误差比单项窜动时的变化趋势小，且误差结果小，这是由于轮对往复窜动时，直径测量轮在测量圆左右来回转动并移动，且轮对踏面是特殊的弧线，综合转动后直径测量轮转动的角度数基本一致。当然，镟修时也应该重视该误差，在机床加工前以及测量完毕后将该误差考虑到加工的目标直径上，避免粗车结束后出现轮径超差等现象。

4 结语

该文基于RecurDyn仿真平台，建立了U2000型数控不落轮车床直径测量系统的动力学模型，研究了测量系统的特性，分析了轮对单项窜动、往复窜动对轮对直径测量值准确性的影响，得出以下3点结论：1） 轮对无论是单项窜动还是往复窜动都会影响轮对直径测量值的准确性。单项窜动的影响最为明显，误差将随着窜动量的增加而迅速增大，过大的窜动量将会造成粗车结束后的轮径超差报警。往复窜动也会影响轮对直径测量值的准确性，虽然其效果不如单项窜动明显，但是其对直径测量轮的冲击较大，对直径测量轮的磨损较单项窜动更明显。2） 该文模拟了LM32磨耗型新车轮，但实际上车辆存在轮对表面覆盖有均匀的黑硬皮、轮对不圆度过大且踏面有剥离和擦伤等缺陷。因此，实际镟修时轮对的单项窜动和往复窜动对轮对直径测量值的准确性影响会增加。3） 针对轮对轴向窜动给测量和镟修工作造成影响的问题，借助多体动力学仿真技术对其特征和机理进行研究，结果具有参考价值，为故障的解决和机床的优化提供了参考。