基于C4.5决策树的自主步态选择算法

陈光荣 王军政 郭盛 侯博文

1.北京交通大学机器人研究中心北京100044 2.北京理工大学复杂系统智能控制与决策国家重点实验室北京100081 3.北京市轨道交通线路安全与防灾工程技术研究中心北京100044

艾萨克·阿西莫夫在《我,机器人》[1]中订立了“机器人三定律”,要求机器人具有决策、学习和优化能力.显然,人工智能对机器人尤为重要.机器学习作为人工智能的核心问题之一,被广泛地应用到生活中的各行各业[2−3].如,在RoboCup 比赛中,为了提高AIBO 机器人的运动速度和稳定性,一些研究学者利用策略梯度法和遗传算法等机器学习方法来优化机器人的步长、步频等步态参数[4−6].众多研究学者基于Little Dog 提出了不同的机器学习算法进行机器人行走控制,实现了在复杂地形下的行走跳跃[7−8].为实现Little Dog 攀爬台阶任务,Kolter J等利用微分符号策略梯度法来优化机体后移的位移,以便完成攀爬动作[9].Kolter J、Kalakrishnan M 以及Zucker M 等都将分层强化学习作为机器人运动规划算法的主要框架[10−12].Belter D 在六足机器人Messor 的运动规划中对机器学习算法进行了大幅度优化,实现了在线地形图生成和路径规划[13−14].谷歌DeepMind 团队曾开发出一款人工智能围棋程序AlphaGo[15−16],打败了围棋世界冠军.近年来,该团队又用AI 教双足和四足模型如何走路、模仿、跳跃、格斗,适应各种地形环境等[17−19],逐渐开辟了一个足式机器人步态规划与控制的新方向.

足式机器人运动控制研究[20−23]日趋成熟,人工智能机器学习在足式机器人方面的应用还需要更深入的探索和研究[24].随着机器人学的迅速发展,人工智能的作用越来越突出.人们对足式机器人的要求已经不只是一些简单的、重复性的机械动作,或者单纯的行走跳跃,机器人应当能作出更好的、更优化的动作,能够自我学习以适应地面环境和外界干扰,并根据所处环境找到最优路径作出动作决策等[25−26].

传统的足式机器人步态规划算法通常是规划给定目标约束下,从起点到终点的路径,对于机器人通过此路径采用什么样的步态,并没有给出明确的说明,且目标约束大多是最短时间或最短路径,相对较为片面.

本文研究的问题就是在给定了4 个主要因素(即新增的目标约束):四足机器人所在地形的地形复杂度,所需的行进速度、所要求的行走能耗和应当保证的稳定性水平下,机器人的自主步态选择问题—是选择静步态好还是动步态好.针对此问题,采用C4.5 决策树理论进行了研究,并得到了此条件下的静动步态自主步态选择决策规则.为了验证算法有效性,结合A*路径规划算法,改进A*算法的总代价函数,将行走路程、行走时间、行走地形起伏量(即地形复杂度)、行走稳定性、行走速度、行走能耗等6 个目标加权融入其中,同时在后4 个目标中加入C4.5 算法决策静动步态的影响,使路径规划相对更为合理,综合因素更全面.

因此,为解决机器人在一定复杂度的地形下[27−28],根据设定的能耗[29−30]、速度[31]和稳定性能自主的决策进行静步态或动步态行走问题[32−33],提出一种基于C4.5 决策树[34−35]的步态自主选择算法.

1 四足机器人

1.1 四足机器人模型

利用Webots 搭建的仿真模型和对应的坐标系统分别如图1和图2所示.机器人单腿3 个自由度:髋关节2 个自由度,膝关节1 个自由度,前后腿均为肘式配置,机器人的机械结构参数如表1所示.

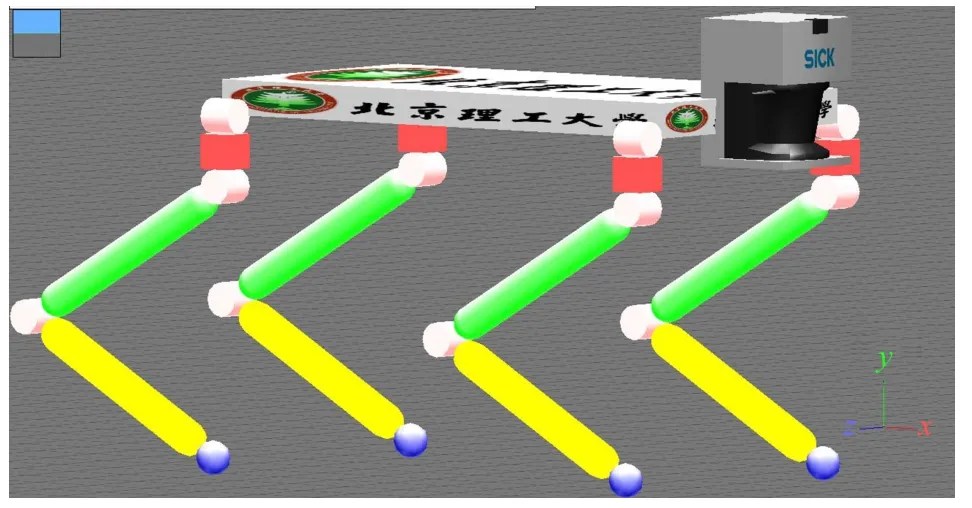
图1 四足机器人仿真模型Fig.1 Simulation model of quadruped robot

表1 机器人系统参数Table 1 System parameters of quadruped robot

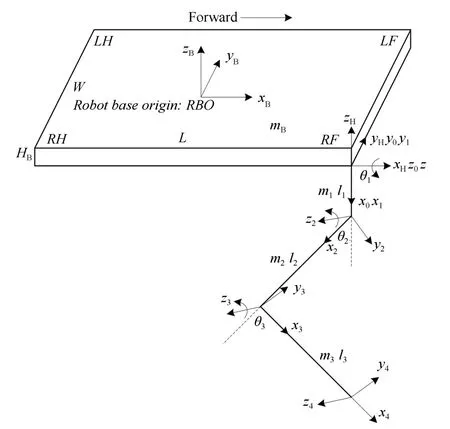
图2 四足机器人坐标系统Fig.2 Coordinate system of quadruped robot

1.2 四足机器人步态类型

从仿生学角度看,四足动物的步态可分为静步态和动步态.静步态指具有静态稳定性的步态,即身体静止时或行走的时时刻刻都满足平衡条件,不会倾倒,其速度较慢,通常有3 条及以上支撑腿,如爬行(walk)步态;反过来,机器人需要不断地切换支撑腿才能保证身体不倾倒的步态就是动步态,其速度较快,通常有两条甚至一条支撑腿,如对角步(trot)、飞跑(gallop)、跳跃(bounding)等.四足动物会根据自身的行走速度需求自动调整步态参数(步长、步频、占空比等)和类别(静、动步态).本文主要研究四足动物行走中最常见的两种步态:walk 静步态和trot动步态的规划方法和平衡控制策略.

1.3 四足机器人步态选择依据

显然,地形复杂度是步态选择的一个重要依据.在不同地形下,四足机器人采取的静动步态不同以便更好地通过.四足机器人的静步态虽然速度慢,行走能耗较高,但稳定性好,具有很强的地形适应能力,可适应高复杂度地形;动步态则正好相反,动步态虽然速度快,行走能耗较低,但稳定性差,地形适应能力较弱,更适应低复杂度地形.因此,当地形复杂度低时,静动步态都可以选择,但需要综合考虑速度、行走能耗和稳定性要求;当地形复杂度高时,更适宜选择静步态以首要保证机器人的运动稳定性.因此,本文以地形复杂度、速度、行走能耗和稳定性为4 个主要选择依据展开自主步态选择算法研究.

地形复杂度的量化指标为STCI.地形越复杂,STCI越大,两者正相关.参考标准差的概率统计意义,其表示一个数据集个体间的离散程度,可用来衡量地形复杂度(地形仅针对足式机器人可穿越地形,非不可穿越障碍).从数学角度上看,当标准差为零时,数据集个体间的差异为零,即个体完全相同;当标准差越来越大时,数据集个体间的差异也越来越大.从物理角度上看,在地面上均匀地选取数据采集点,仅取其高度值或相对高度值,当这些地面点高度值的标准差为零时,这些地面点高度值间的差异为零,即地面是完全平坦的;当这些地面点高度值的标准差越来越大时,这些地面点高度值间的差异也越来越大,即地面越来越复杂崎岖,地面复杂度也越来越高.

在此给出具体的地面选取方法和地形复杂度简易计算方法如图3,因为地形的复杂程度或机器人的越障能力与其自身的尺寸大小和步长有关,所以本文选取机器人机体中心往外约两倍面积的地面区域Aterrain≈2Arobot,取当前行走1/2 步长S/2 作为最小网格将该区域网格化,计算所有网格交点的高度值hi(i=1,...,N)的标准差作为地形复杂度:

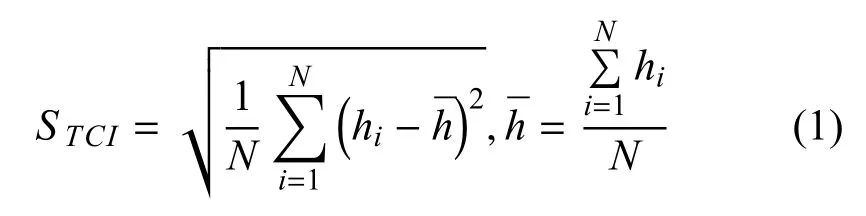
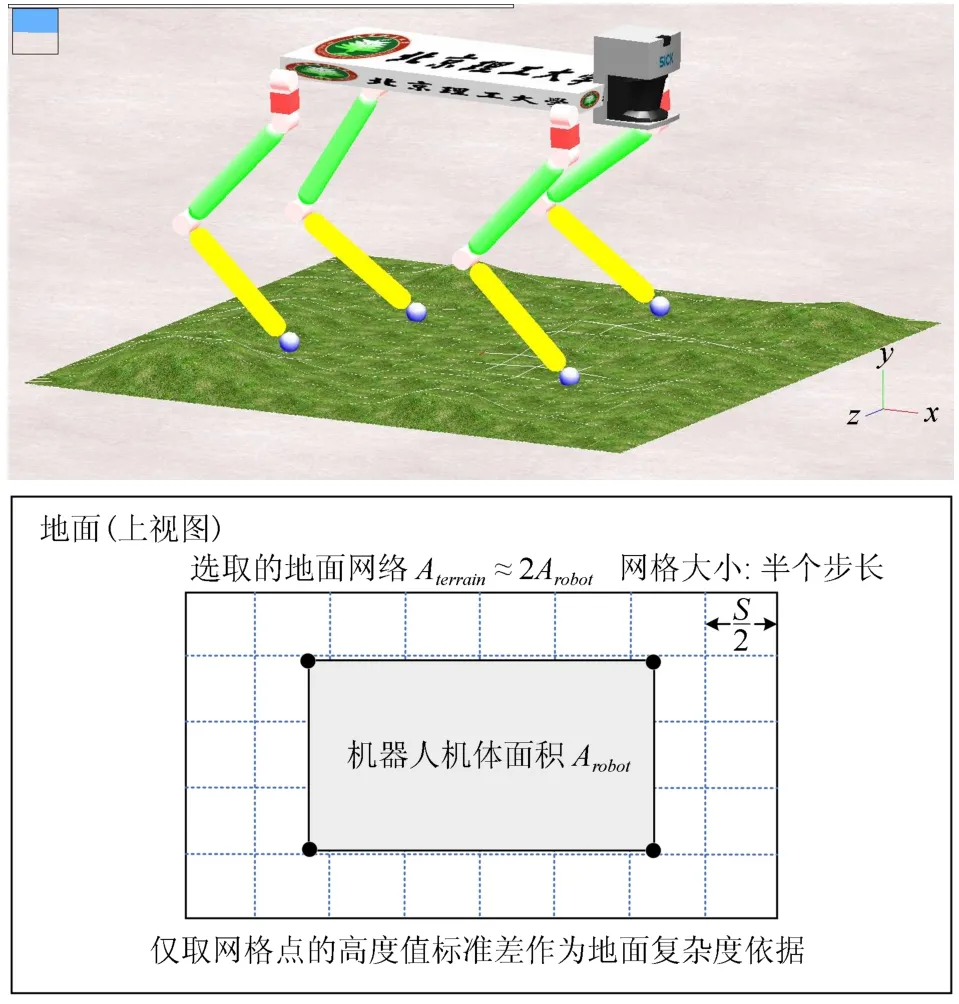
图3 地形复杂度计算方法Fig.3 Calculation method of terrain complexity index

行走能耗的量化指标为η,指单位步行距离执行器所做的功的总和,即

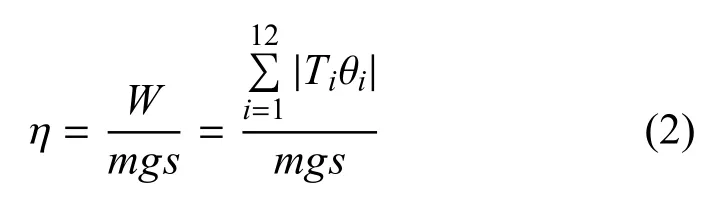
其中,s为步行距离,θi和Ti分别为机器人的12 个关节的关节角度和力矩.

静步态稳定性的量化指标为稳定裕度Ss,具体是指机器人的压力中心点与多边形每条边的最短距离,即

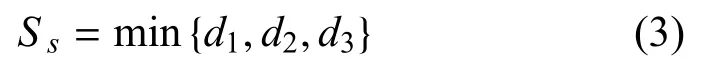
其中,d1,d2,d3为质心点投影到支撑多变形各边的距离,如图4所示.

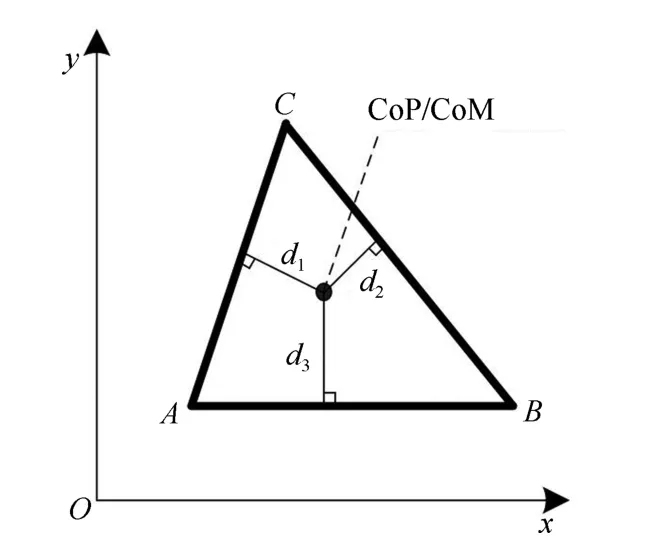
图4 稳定裕度Fig.4 Stability margin

动步态的量化指标为Sd.简单以一个步态周期内姿态角αi,βi,γi(i=1,...,N)的标准差的平方根的倒数作为动态稳定性参考,即

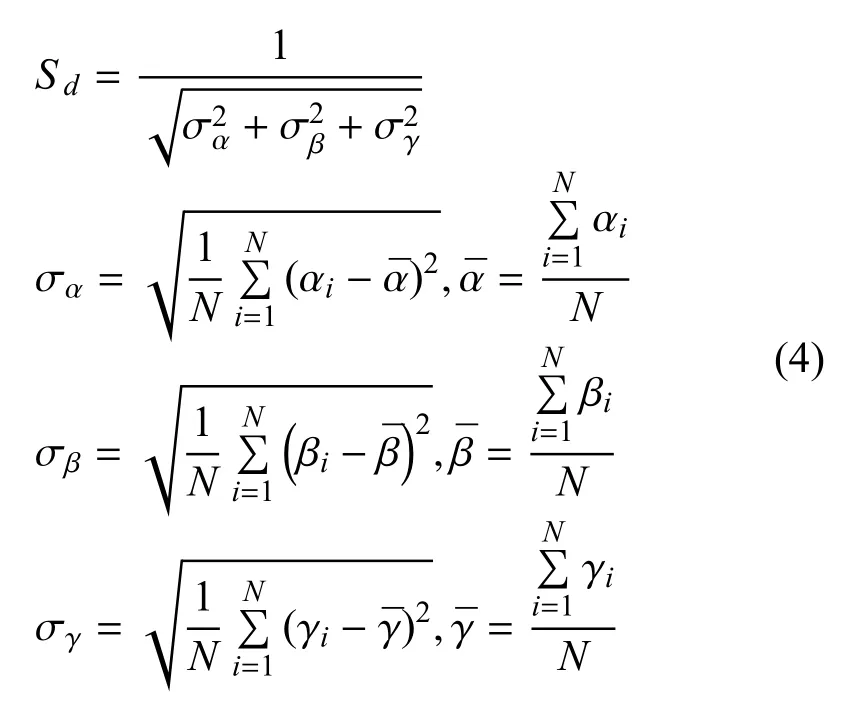
为了获取影响机器人步态选择4 个因素的内在联系,进一步分析静步态的速度、行走能耗、稳定性三者之间的关系,通过改变步态和步态周期来对比4种不同速度下,静步态的速度、行走能耗、稳定性三者之间的关系,如图5所示.可以看出静步态速度的提升直接导致了稳定裕度的下降,但是行走能耗也得到了降低.

同时,进一步分析静步态的速度、行走能耗、稳定性三者之间的关系,根据仿真比较在平地动步态稳定行走时不同速度与能耗和稳定性的关系,如图6所示.可以看出与静步态行走相类似的结果,速度的增加会导致稳定性下降,使行走能耗变大.

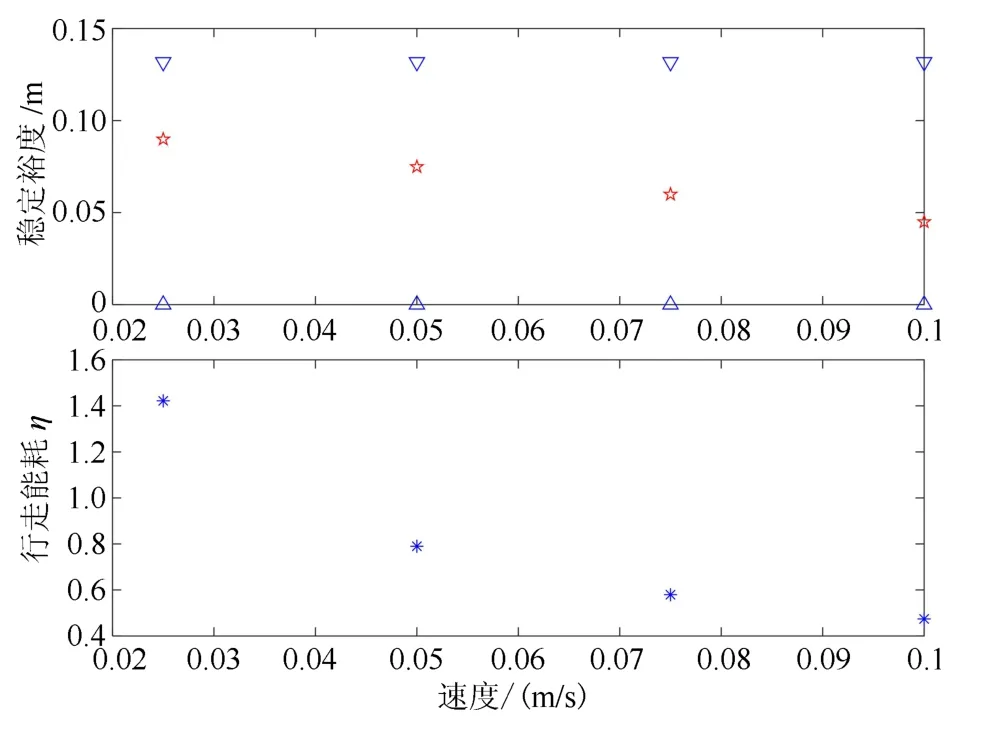
图5 静步态的速度、行走能耗、稳定性三者之间的关系(∇,∆,★分别为上下限和均值)Fig.5 The relationship among the speed,cost of transport and stability of static gait(∇,∆,★are the upper limits,lower limits and mean value,respectively)

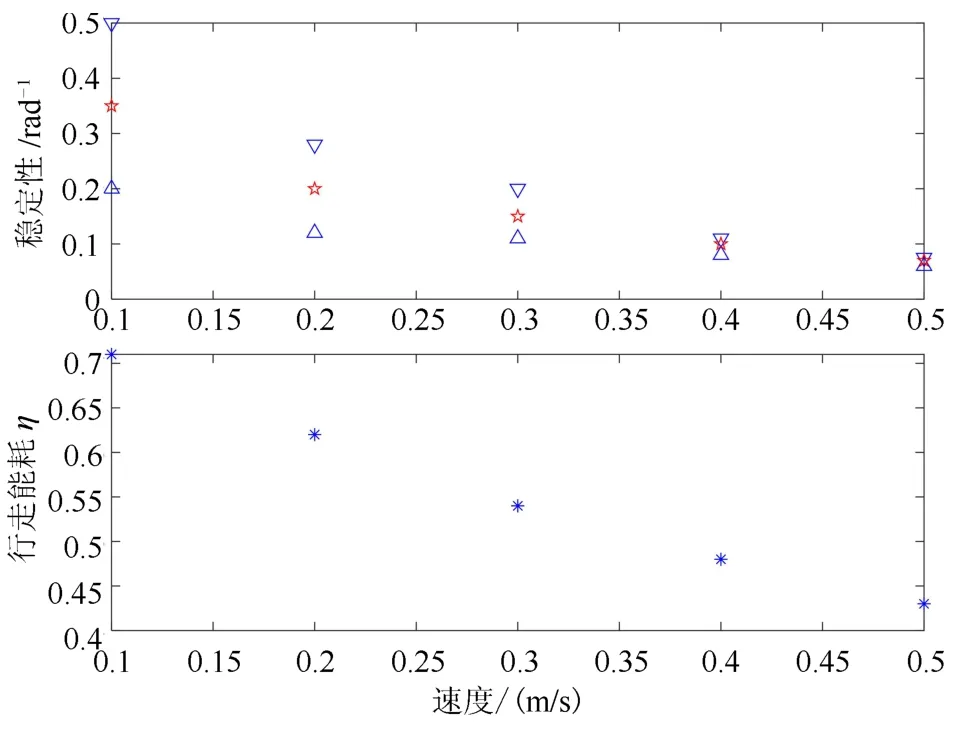
图6 动步态的速度、行走能耗、稳定性三者之间的关系(∇,∆,★分别为上下限和均值)Fig.6 The relationship among the speed,cost of transport and stability of dynamic gait(∇,∆,★are the upper limits,lower limits and mean value,respectively)

2 自主步态选择算法

2.1 C4.5 决策树算法

决策树(Decision Tree,DT)算法是一种基于数据的归纳推理分类方法,它不需要过多领域背景知识和固定的诊断模型,即可通过对决策表形式的无序样本数据进行推理学习,建立用于分类判断的决策树,从中提取清晰直观的分类规则[36].常见的决策树算法有:ID3、C4.5 和CART.相比于ID3 和C4.5,CART 不但可以分类还可以作回归分析,但是CART 只能产生二叉树,而ID3 和C4.5 可以多叉,而且CART 更适合于大样本,ID3 和C4.5 适合于小样本.C4.5 本身是ID3 的继承和改进,解决了ID3 不能处理连续变量(只能处理分类变量)和对缺失值敏感的问题,故本文采用C4.5 决策树方法.

如图7所示,决策树的建立需要经过初始决策树的生成和决策树剪枝两步.C4.5 决策树算法流程如算法1.在用C4.5 算法生成初始决策树后,为避免训练样本数太少导致的过拟合现象和初始决策树较为复杂难理解的问题,需要对初始决策树进行剪枝(pruning),剪枝方法有两种:预剪枝(prepruning)和后剪枝(postpruning)[36].预剪枝是指在决策树生成的过程中,在属性划分前对每个节点先进行估计,如果当前节点的划分不能带来决策树泛化能力或分类精确性的提升,则停止划分并将当前节点标记为叶节点;后剪枝是指先从训练集生成一棵初始决策树,然后自下而上地对非叶节点进行考察,如果该点对应的子树替换为叶节点,可以带来决策树泛化能力或分类精确性的提升,则将该子树替换为叶节点.

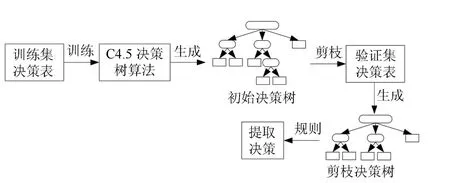
图7 决策树算法规则提取流程Fig.7 Rule extraction process of decision tree algorithm

算法1.C4.5决策树算法输入:训练集决策表:训练集D={(x1,y1),(x2,y2),...,(xn,yn)}与属性集A={a1,a2,...,am}输出:以node 为根节点的决策树1:function Build DT(D,A)建树函数2:生成节点node;3:if D 中样本全属于同一类别C then 4:将node 标记为C 类叶节点;return 5:end if 6:if A=∅,D 中样本在A 上取值相同then 7:将node 标记为D 中样本数最多的类的叶节点;return 8:end if 9:从A 中选择最优属性,即a∗=arg max GR(D,a)增益率最高的属性;10:for a∗的每一个属性值av∗do 11:为node 生成一个分支;令Dv 为D 中在a∗上取值为av∗的样本子集;12:if Dv 为空then 13:将分支节点标记为D 中样本数最多的类的叶节点;return 14:else 15:以Build a∈A DT(Dv,A{a∗})为分支节点;16:end if 17:end for 18:end function

2.2 建立初始决策表

通过1.3 节分析可知,机器人静动步态的影响因素主要有稳定性、速度、行走能耗、地形复杂度4 个,将它们取为条件属性,且均可以取高、中、低3 个等级,如表2和表3所示(注:只取行进速度分析).

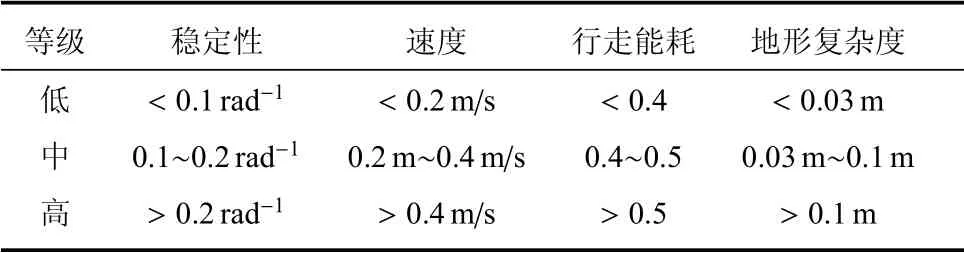
表3 动步态条件属性表Table 3 Condition attribute table of dynamic gait

决策树形即静步态和动步态两种.利用条件属性和决策属性,结合仿真效果建立初始决策表,并在仿真同时收集样本数据,从样本数据中随机抽取30组作为训练集,30 组作为验证集,分别如表4和表5所示.

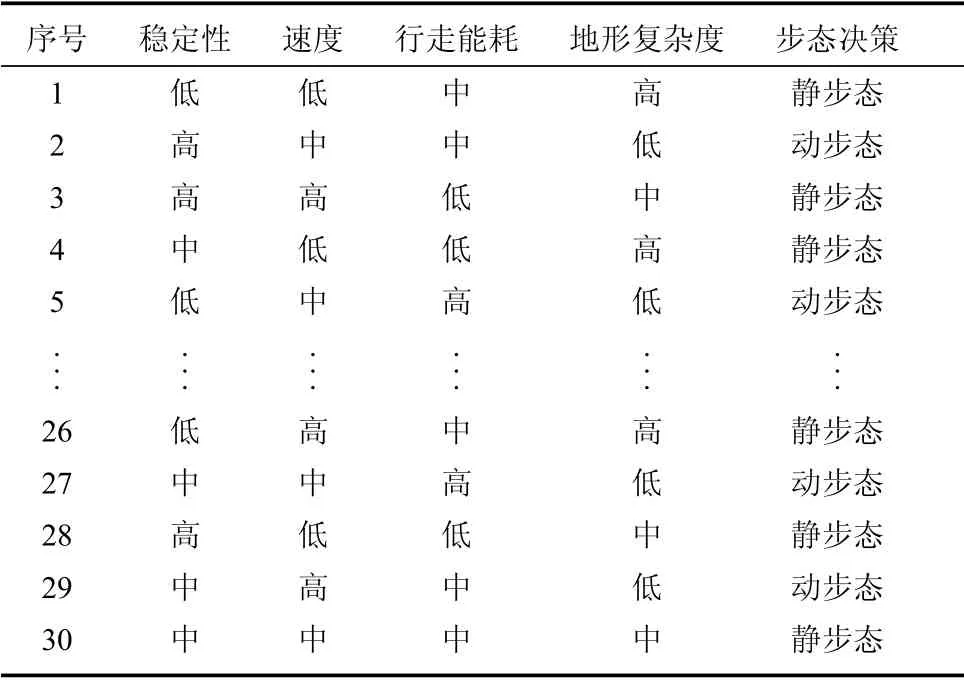
表4 训练集样本示例Table 4 Training set samples

2.3 建立决策树

对表4中的数据利用C4.5 算法1 生成初始决策树,如图8所示.

为提高决策树分类准确性,利用表5中的验证集数据,对其进行后剪枝,发现初始决策树中非叶节点对应的子树替换为叶节点并不能提要高其原来的验证集精度96.67%.

从图8决策树可以看出,影响步态4 个因素的主次关系为:地形复杂度>稳定性>速度>行走能耗.通过1.3 节分析可知,地形复杂度会影响其他3 个因素.决策树偏向于选择静步态,因为稳定是机器人执行任务的基础.在满足稳定性前提下,动步态可以很容易提高速度.行走能耗的分析也并不是多余的,因为给予更多的能量,静步态可以更好地控制住速度,尤其是横向速度.

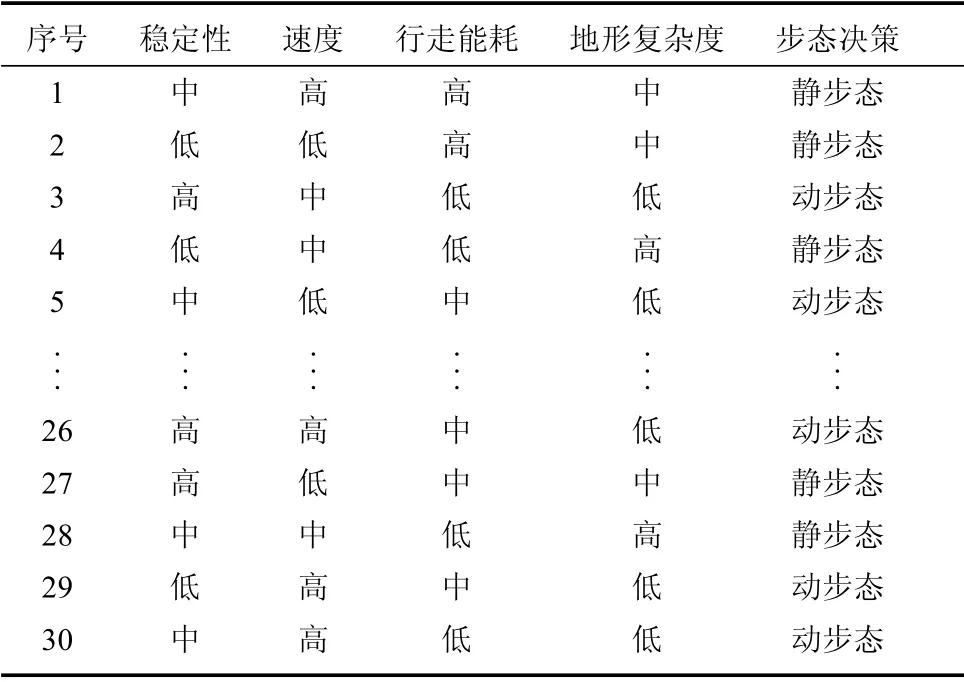
表5 验证集样本示例Table 5 Verificatio set samples

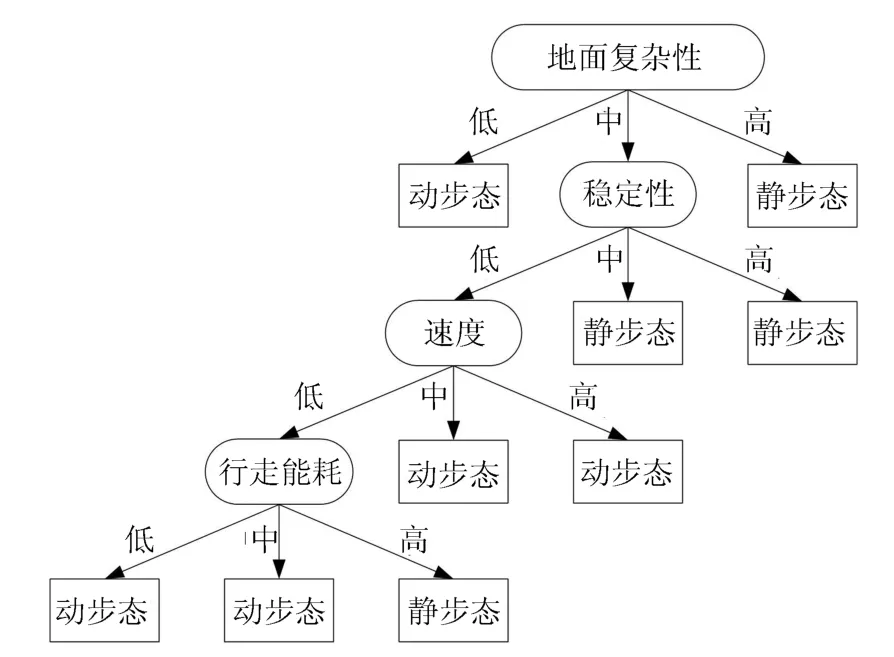
图8 C4.5 算法生成的决策树Fig.8 Decision tree generated by C4.5 algorithm

2.4 提取决策规则

根据剪枝后的决策树,可以提取决策规则“IF 条件THEN 决策”模式如下:

1)IF 条件:地形复杂度低

THEN 决策:动步态

2)IF 条件:地形复杂度中,稳定性低,速度低,行走能耗低

THEN 决策:动步态

3)IF 条件:地形复杂度中,稳定性低,速度低,行走能耗中

THEN 决策:动步态

4)IF 条件:地形复杂度中,稳定性低,速度低,行走能耗高

THEN 决策:静步态

5)IF 条件:地形复杂度中,稳定性低,速度中

THEN 决策:动步态

6)IF 条件:地形复杂度中,稳定性低,速度高

THEN 决策:动步态

7)IF 条件:地形复杂度中,稳定性中

THEN 决策:静步态

8)IF 条件:地形复杂度中,稳定性高

THEN 决策:静步态

9)IF 条件:地形复杂度高

THEN 决策:静步态

3 仿真验证

给定地形如图9,设定机器人要从当前初始位置走到黑框目标位置.首先,利用生成的决策树图8,对整个地形进行静动步态选择决策,如图10所示,其中绿色区域为适宜动步态行走区域,红色区域为适宜静步态行走区域,黄色区域为静步态和动步态皆宜行走区域.

然后,设定完成该行走任务可以具有以下6 个目标约束:

1)Js最小:机器人行走路程最小,即路径长度s最短;

2)JT最小:机器人行走时间最小,即总用时T最短;

3)JTCI最小:机器人行走地形起伏最小,即STCI最小;

4)JS最大:机器人行走稳定性最大,即Ss或Sd最小;

5)Jv最大:机器人行走速度最快,即最大;

6)JCoT最小:机器人行走能耗最小,即η 最大.

注意此种设定相对更为合理,因为人从一个位置到另一个位置正常行走时,也会选择更平坦、更省力、更不容易摔倒、速度更快、时间更短、长度更短的路径.而传统的A*算法[37]和文献[38]提出的改进A*算法都只考虑目标约束1 的路径最短方式,相对较为片面.

为了避免出现多目标优化的Pareto 前沿面,可将6 个多目标加权为一个单目标,设计任务总代价函数为

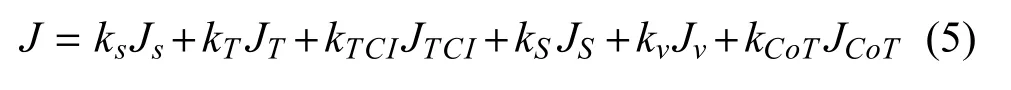
其中,k•>0 为相应优化目标J•的加权系数,要突出某一个目标则加大其系数即可.k•<0 为奖励动作,暂不考虑.

将式(5)融合到文献[38]中提出的改进A*算法的估价函数

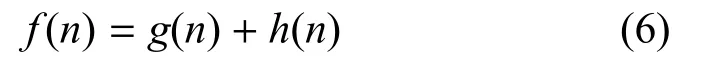
其中,f(n)是从初始节点经由任意节点n移动到目标节点的估价函数,g(n)是从初始节点移动到节点n的实际代价,h(n)是从节点n到目标节点的估计移动代价.采用式(5)代替欧几里得距离作为两点之间的移动代价.当ks>0,kT=kTCI=kS=kv=kCoT=0 时,则该算法与文献[38]的改进A*算法相同.

最后,利用C4.5 决策树分析得到的图8,结合式(5)修正的改进A*路径规划算法[38]进行仿真,可得出如图10所示的3 种典型规划路径,其仿真目标约束和相应参数如表6所示.根据当前行走任务执行的目标约束要求选择最佳路径,如果只要求路径最短,则选择路径1;如果既要求路径短又要保证稳定性,则选择路径2;如果只要求时间短,则选择路径3.相比与文献[38]的改进A*算法,该方法可根据行走任务执行需求生成不同的路径,更具有一般性和适应性.

图9 机器人行走地形环境Fig.9 Terrain environment for robot walking

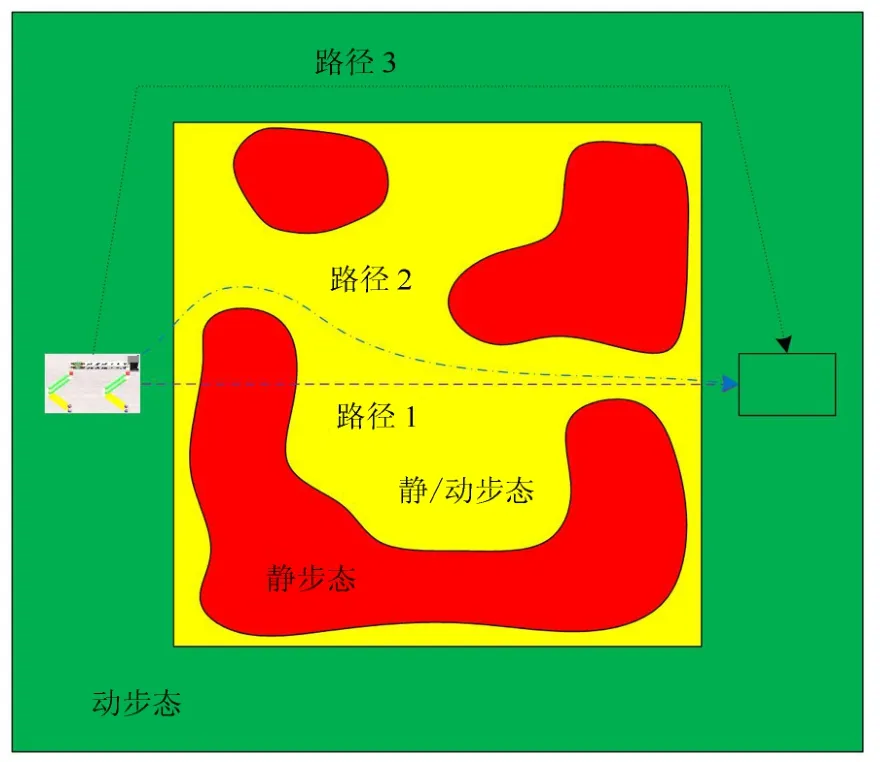
图10 静动步态选择决策与路径选择Fig.10 Static and dynamic gait selection decision and path selection

表6 仿真参数Table 6 Simulation parameters

4 结论

以地形复杂度、速度、行走能耗和稳定性作为4个主要选择依据,研究一种基于C4.5 决策树的自主步态选择算法.主要贡献如下:

1)研究影响四足机器人静动步态行走的4 个主要因素:地形复杂度、速度、行走能耗和稳定性,并分析这4 个因素之间的内在联系;

2)将以上4 个因素作为静动步态选择依据,研究一种基于C4.5 决策树的自主步态选择算法,通过训练得到静动步态自主决策规则;

3)结合式(5)修正的改进A*路径规划算法,通过仿真验证所提出算法的有效性和可行性.

该算法也存在一定的局限性,算法中提出了一种地形复杂度的定量计算方法式(1),即算法局限所在.在仿真环境中,地面网格各点的高度值容易得到,但在实际应用中,需要通过激光雷达等传感器进行采集(可为相对高度值),存在采集误差、采集盲区等问题,容易影响到地形复杂度计算结果的准确性;同时,地形复杂度计算结果的准确性也受到选取有效地面网格区域的差异,网格大小等因素影响.在实际应用中,以上局限也可以通过工程的方式加以弥补和修正,如增加激光雷达等传感器数量和精度等.此外,在计算误差允许范围内,地形复杂度的计算结果也是可以作为步态选择的参考依据.

该方法可以运用到其他类型足式机器人.同时,带有奖励性质(k•<0)的路径规划也是未来需要做的工作.