基于熵值法和单目标规划的物资分配模型＊

2021-04-13焦荟蓉朱敬华奚赫然

科技与创新 2021年6期

焦荟蓉，朱敬华，奚赫然

基于熵值法和单目标规划的物资分配模型＊

焦荟蓉，朱敬华，奚赫然

（黑龙江大学，黑龙江哈尔滨 150080）

新冠肺炎疫情造成各省物资短缺。根据所定的属性，利用熵值法计算各个资助点所在区域的紧急救援权重。然后通过单目标规划的方法，以需求满意度为目标，结合熵值法得出的权重，得到最大化灾区整体需求满意度函数，从照顾范围和风险程度双方面考量，最终得出合理的解集。最后对此算法进行了验证，证明该方法对于物资分配提出的方案合理可行。

物资分配模型；熵值法；单目标规划；数值实验

为了给各待资助点进行评级，通过分析发现影响一个待资助点的待资助程度的因素主要有该待资助点的灾民恐慌度、当月感染人数、当月死亡人数、待资助点拥有的医院数量、待资助点拥有的医护人员数量、待资助点本年GDP和救灾物资未满足度这些属性。以疫情严重的2020年为例，将上述属性的数据从国家统计局提取出。下面对这些数据先进行预处理，无量纲化处理后，利用熵值法分析出各个待资助点的紧急救援权重。

1 熵值法对各资助点需要资助程度进行评价

假设在一个区域中，有多处地点需要资源帮助。一些地区可能归属于同一个省份，本文将属于一个省份的所有受灾点抽象为一个待资助点。

在各项指标中，灾民恐慌度、感染新冠肺炎人数、当月死亡人数和救灾物资未满足度为正向指标，其余是负向指标。负向指标在这里指代越小，该待资助点越需要物资来帮助；正向指标指代值越大，该待资助点越需要物资来帮助。由于各指标数量级等并不统一，因此要对其进行标准化处理，消除量纲。具体方法如式（1）（2）所示。其中，右侧ij为第个待资助点的第个评价属性的实际值，左侧ij为第个待资助点的第个评价属性的归一化结果，下文中ij都指代归一化后的ij；为31个内陆省份；为上述7个评判属性。

正向指标公式：

负向指标公式：

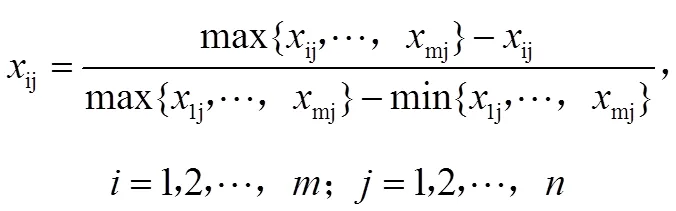
熵值法的指标权重值通过熵的计算得到，由样本数据本身决定，具有客观性和科学性。熵值法的步骤如下。

第一步，将各指标同度量化后的结果取出，计算第个待资助点的第项属性指标值占所有待资助点该属性指标值的比例ij，如式（3）所示。得到第个待资助点某个指标在所有待资助点的该指标中所占比例。

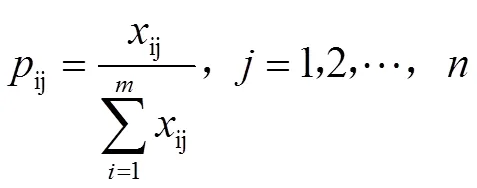
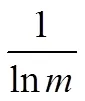
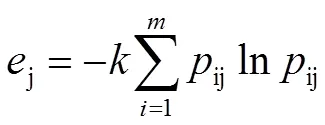
第三步，计算第项指标的差异性系数i。对于第项指标，指标值ij的差异越大，对方案的评价需要资助的力度的作用越大，熵值就越小。差异性系数i的计算如式（5）所示。因此，i越大指标越重要。

j=1－j（5）

第四步，定义权数j，权数计算公式如式（6）所示。在这里得到的权数是每个属性所占的权数。

第五步，得到每个待资助点的权重i。利用算出的ij与属性权重j相乘并求和，得到最终的每个资助点权重，如式（7）所示：

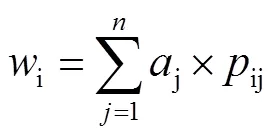
2 单目标规划

本文的规划目标为需求满意度。简单来说，满足待资助点需求的量越多，需求满意度越大。因为疫情具有突发性，所以第一时间可供应急的物资有限，应急物资短缺现象严重。算法的决策结果希望最大化满足应急物资需求。参考了文献[1]的相对需求比例函数表示需求满意度，将待资助点的需求满意度（）定义如式（8）所示，式中的表示待资助点集合。=｛1，2，…，｝，∈；i表示初始时刻待资助点对应急物资的需求量；i表示到待资助点的实际应急物资运送量；i表示待资助点所在区域的紧急救援权重，这里，权重的值由上述熵值法来确定。

式（8）中：i为待资助点的实际物资满足量与需求量之比。

式（9）中：为各类物资的编号。

由于结合了各待资助点需要资助的力度，确保了最终的需求满意度既不会因为急于满足过多要求而忽略了风险严重地区的呼声，又避免了对高需求地区的单一分配而忽略其他地区的需求。得到的最优结果综合了照顾的范围和风险程度，是一个较为合理的分配结果。

式（10）中：为最大化灾区整体需求满意度。

约束条件表明sum事件发生的背景属于大规模突发事件，因此在进行初始资源配置救援方案时应急资源供不应求。sum表示可支援的总量。在这里抽象为只有一个地点可以支援。各待资助点资助数量只能为整数。具体约束条件如下所示：

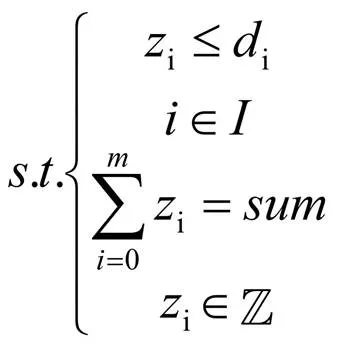
3 数值实验及结果分析

本文所构建的模型和算法已在多个示例上进行了计算，均获得较满意的结果。在此模拟一个较简单的三个待资助点的算例说明根据这个算法资源分配问题的求解过程。设计算例如下。

各临时救援点的物资需求向量为：i=（1，2，3）=（10，14，17）。可资助总量为30。各待资助点的各属性如表1所示。

若影响待资助点的属性有3个，分别为attribute1、attribute2、attribute3。若attribute1、attribute2为正向指标，attribute3为负向指标。

表1 计算属性权值属性

待资助点1待资助点2待资助点3 attribute132.926 567.721 912.312 4 attribute20.8470.630.921 attribute3524439842

首先，根据原始数据，利用式（3）、式（4）、式（5）、式（6），计算出ij、熵值、j和j的值，如表2所示。

表2 第一步计算后的表格

待资助点1 p值待资助点2 p值待资助点3 p值熵值差异性系数属性权重 attribute10.271 20.727 9830.000 70.537 30.462 60.382 7 attribute20.427 00.000 5720.572 40.625 30.374 60.309 9 attribute30.440 80.558 5680.000 50.628 50.371 40.307 2

根据表2计算出的数据，代入式（7），利用表2中ij和j，得到最终的权值结果，最终结果如表3所示。

表3 各待资助点权重值

待资助点名称权值待资助点10.37 待资助点20.45 待资助点30.18

下面利用C语言编程，代入单目标规划给出的各个方程，按照算法给出的目标函数和约束条件，得到了如下结果：算法给出的分配方案是i=（1，2，3）=（0，13，17）。