电容器对交流电路动态变化的影响探讨
2021-04-12徐地虎庄勇飞
徐地虎 庄勇飞
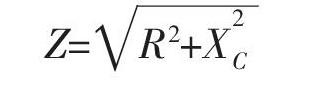
摘 要:电容器具有通交流、阻直流的特性,在含交流电源电路中电容器不断地进行充电和放电,宏观上表现为交流“通过”了电容器。电容器在通交流电时具有容抗,且电容器两端的电压与电流存在相位差。文章通过交流电路分析,得到容抗的表达式,分析影响容抗大小的因素,得出电压和电流之间的相位關系,并与纯电阻电路进行对比,最后分析电容器对交流电路动态变化的影响。
关键词:电容器;交流电路;动态变化;相位
中图分类号:G633.7 文献标识码:A 文章编号:1003-6148(2021)3-0059-4
1 问题缘起
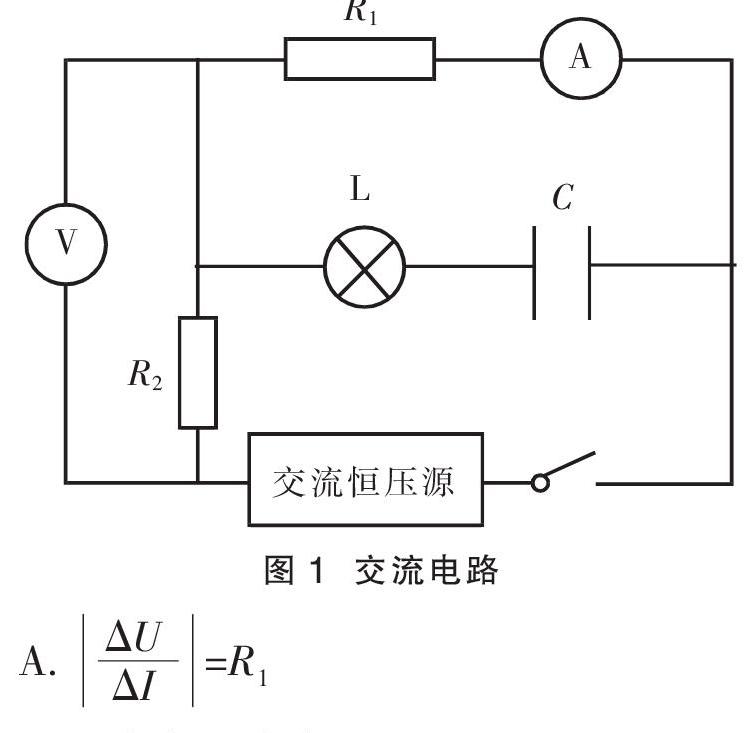
从江苏省南京市六校联合体2020届高三下学期5月联考第5题说起。
案例:如图1所示,电源为交流恒压源,即无论电路中的电阻如何变化,接入电路的交流电压始终保持恒定。R1、R2阻值保持不变,理想交流电压表■与理想交流电流表■的示数分别为U、I。当恒压交流源的频率变大时,理想电压表■与理想电流表■的示数变化量分别为ΔU、ΔI,下列说法正确的是()
A. ■=R■
B. U变大,I变大
C. 灯泡变暗,I变小
D. ■=R■+R2
参考解答:恒压交流源的频率变大,根据容抗的表达式XC=■可知,容抗变小,电路的总阻值变小,干路中的电流增大,U变大,R1两端的电压变小,电流表读数变小,通过灯泡的电流增大,B、C选项都错;根据闭合电路欧姆定律ε=U+IR1可知,■=R■,答案选A。
在参考解答中,交流电源的频率增大,电容器的容抗减小,其他的分析过程与直流电路分析过程类似,相当于在直流电路中滑动变阻器阻值变小,但并没有考虑到容抗对应的电流与电压之间的相位关系,正是这个原因导致答案出现问题。
2 电容器的容抗
定义:电压有效值和电流有效值之比,叫作电路元件的阻抗。电容器对应的比值叫作容抗。
图2所示为只有交流电源和电容的纯电容电路,交流电压为U,电容为C。设电路中的尺寸为l,交流电源频率为f,光速为c,若满足
■<<■(1)
则可认为电路对电源变化的响应几乎不需要时间。在这种近似下,电流将随电源电动势同步变化,(1)式称为似稳条件。以下研究的电路都满足似稳条件。
设所加交流电的交变电压为
u=U0cosωt(2)
根据闭合电路欧姆定律,电容器两端电压满足
u=■(3)
q为电容器所带电荷量,则电路中的电流可写为i=■(4)
q增大时,dq>0电容器充电;q减小时,dq<0,电容器放电。将(2)(3)式代入(4)式有
i=U0ωCcos(ωt+■)=I0cos(ωt+■)(5)
电压与电流最大值之间的关系有
U0=I0■=I0XC(6)
有效值对应关系为
U=I■=IXC(7)
其中
XC=■=■(8)
称XC为容抗,单位与电阻的单位相同,也是欧姆。从(8)式可以看出,f越大, XC越小,电容器通交流电;f越小,XC越大,极限情况是f=0,此时为直流电,XC→∞,即电容器阻直流电。
与此同时,比较(2)和(5)式可以发现,电压与电流的相位不同,电容器上的电压相位相比“流经”电容器的电流的相位落后■,电流与电压随时间变化的图像如图3所示。将该结果与纯电阻电路进行对比。
如图4所示的纯电阻电路,电路中电压和电流服从欧姆定律,若交流电压依然如(2)式所示,则
i=■cosωt=I0cosωt(9)
其中I0=■,电流、电压有效值满足
U=IR(10)
可以看出,从最大值与有效值表达式上看,R与XC作用相当,但在纯电阻电路中,电阻两端的电压与电流相位相同,这与纯电容电路有差别。正是由于这种差别,影响了含容交流电路的动态变化分析。为此,可以利用求解电路的总阻抗对电路做进一步分析。
3 电容器与电阻串联的总阻抗及矢量图解法
如图5所示为电阻与电容组成的串联电路,分析电路的总阻抗。
分析:根据以上对电容器的容抗和电阻的分析可知,若是纯电阻串联或纯电容串联,电阻相加或容抗相加即可,但在电阻与电容串联的电路中,两者在两端的电流与电压的相位关系有差别,不能直接相加,需要重新计算。由于串联电路中各处的电流是相同的,可设电流的表达式为
i=I0cosωt(11)
根据(2)(5)(9)式可知,电阻、电容器两端的电压分别为
uR=I0Rcosωt,uC=I0XCcos(ωt-■) (12)
串联电路的总电压为
u=uR+uC=I0■cos(ωt-φ)(13)
其中
tanφ=■(14)
比较(11)与(13)式,电压相位比电流相位落后φ,电路总阻抗为
Z=■ (15)
正是由于电阻与容抗特点的不同,导致电路的总阻抗满足(15)式,而不是直接代数相加,这也决定了电路中各处的电压和电流分布与直流电路分布的不同。
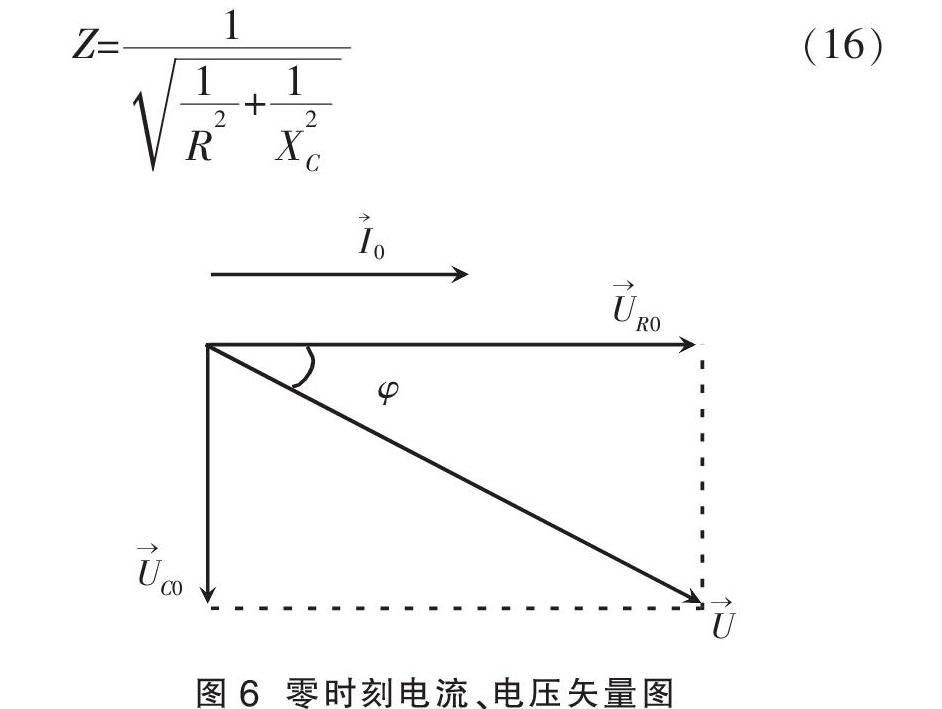
利用矢量图解法能更直观地描述电压与电流之间的相位关系。电流或电压的瞬时值可对应于某矢量在X轴或Y轴的投影。如(12)式所示,uC=I0XCcos(ωt-■)=UC0cos(ωt-■),可对应于■■的矢量以角速度ω逆时针旋转,UC为该矢量在X轴上的投影,ωt-■为相位;uR为uR=I0Rcosωt=UR0cosωt,对应于■■的矢量以角速度ω逆时针旋转,但相位始终比■■超前■,则串联电路中总电压可先求该两个矢量之和,再在X方向投影。将零时刻各矢量放在同一矢量图中,如图6所示,其中电流始终与电阻两端电压同相位,tanφ=■,■以角速度ω逆时针旋转,总电压U为■在X轴上的投影。则电压有效值U=■■,电流有效值I=■I0,根据阻抗的定义可知,电路总阻抗就是(15)式所示。
同样,根据并联电路中用电器两端电压相同,利用矢量图解法,可求得电容器与电阻并联后的总阻抗
Z=■ (16)
讀者可自行画矢量图推导。
根据以上的分析可知,当交流电路中含电容器时,由于电容器两端电压与“通过”电容的电流相位不同,不能简单地利用电阻串并联方法计算总阻抗,利用矢量图解法可以有效、直观地反映电流与电压之间的相位关系,从而可以进一步分析含电容器交流电路的动态变化问题,继续以案例为例进行分析说明。
4 含交流电源电路中电容器对电路动态变化的影响
电路结构如图1所示,设“通过”电容器的电流为iC=IC0cosωt,则灯泡与电容器的电流、电压矢量关系如图7(a)所示,设灯泡的电阻为RL,则tanφ1=■;根据并联关系可知R1两端的电压也为U1,电流中的总电流与各支路之间的电流关系如图7(b)所示,图中■■=■,tanφ■=■;R2两端的电压与通过R2的电流同相位,电路中的总电压与各处电压的关系如图7(c)所示,其中tanφ3=■。
分析电路的动态变化。电路总电压U0恒定,ω增大,XC变小,φ■减小,φ■减小,■20增大,■10减小,■20减小,电流表与电压表测量的是有效值,可知电压表示数增大,电流表示数减小。从以上的矢量图分析可知,R2两端电压与通过R1的电流有相位差,大小关系较复杂,不是简单的线性关系,A、D选项都不正确,此题无正确答案。参考分析中利用ε=U+IR1,事实上ε、U与I相位不同,已不能直接进行简单的代数计算。
因此,在分析含容交流电路的动态变化问题时,根据容抗的变化情况,一般定性分析电路中的电流、电压变化是比较可靠的,但是当要定量计算电路中的电流、电压关系时,则需要考虑电容器两端电压与“通过”电流相位的不同带来的影响,计算相对比较复杂,高中学生不要求掌握,所以在研制相关考题或训练题时应加以考虑。
5 小 结
电容器具有通交流、阻直流的导电特性,容抗XC=■=■,随交流电的频率变化而变化,f越大容抗越小;与此同时,电容器两端的电压与“通过”电流存在■的相位差,这也导致在计算电路总阻抗时不能与电阻阻值直接代数相加。在处理含电容器的交流电路动态变化时,定性分析电路中的电流、电压变化是比较可靠的,但要定量计算电路中的电流、电压变化关系时,则需要考虑相位带来的影响,利用矢量图解法可以有效、直观地分析电路中各部分的电流与电压的相位关系。
参考文献:
[1]程稼夫.中学奥林匹克竞赛教程·电磁学篇[M]. 合肥:中国科学技术出版社,2014.
[2]赵凯华,陈熙谋. 电磁学(第四版)[M]. 北京:高等教育出版社,2018.
[3]中华人民共和国教育部.普通高中物理课程标准(2017年版)[S].北京:人民教育出版社,2018.
(栏目编辑 罗琬华)
