考虑接触非线性的进水塔动力响应分析

张 希，党康宁，韦子琛，陶 伟

(1.中陕核工业集团监理咨询有限公司，陕西 西安 710060；2.陕西省引汉济渭工程建设有限公司，陕西 西安 710010；3.陕西聚源水利工程勘察设计有限公司，陕西 西安 710075)

1 前言

进水塔一般为高耸水工建筑物，其塔体横断面、结构布置、荷载、设计工况、边界条件复杂[1]，作为水利枢纽工程宣泄洪水提供安全通道，其抗震安全性对确保水利枢纽的安全是至关重要的[2]。

众多学者对进水塔进行了弹性范围的动力分析，取得较多成果。多数研究对进水塔进行分析时，通常把进水塔与塔后回填混凝土看成一个整体，必然会导致连接处产生应力集中，与实际不符。塔后回填混凝土为一般不同期浇筑，二者必然存在缝隙，当发生地震时，高耸结构进水塔发生摆动，而塔后回填混凝土很有可能与其运动不一致，二者会发生碰撞或张开，考虑进水塔与回填混凝土的相互作用，即考虑进水塔与回填的接触非线性更加符合实际情况。

本文考虑进水塔与塔后回填互相作用，采用接触单元，对羊曲水电站进水塔进行了非线性的抗震分析。

2 进水塔非线性接触

有限元分析中，接触条件是一类特殊的不连续约束，它允许力从模型的一部分传递到另一个部分。因为只有当两个表面发生接触时才会有约束产生，而当两个接触的面分开时，就不存在约束作用了，所以这种约束是不连续的。分析时必须能够判断什么时候两个表面发生接触并采用相应的接触约束，并能判断什么时候两个表面分开并解除接触约束。

对于进水塔和塔后回填混凝土可采用有限元中的面-面接触，接触单元应用“目标”面和“接触”面实现共享形成接触点对。

2.1 法向接触和切向接触

接触可区分为法向接触和切向接触。法向上，接触压力和间隙的关系见图1。当两个表面被压紧时，施加接触约束，即作用垂直于接触面的压力，接触面之间可以传递任意大小的接触压力。当接触面之间的接触压力变为0时，两个接触面分离，接触约束被移开。可见，接触面之间不会发生互相嵌入，符合实际情况。

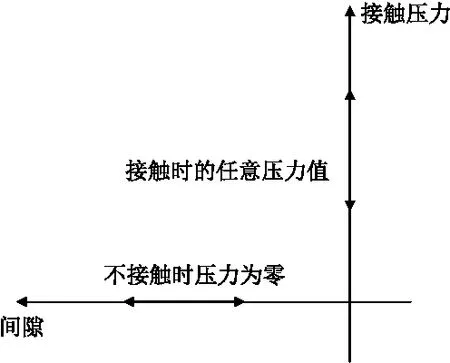
图1 接触压力-间隙关系

进水塔和塔后回填混凝土在接触面之间存在摩擦，接触面之间不仅可以传递法向压力，还可以传递切向剪力(摩擦力)以阻止接触面间的相对滑动。一般用库仑摩擦描述接触面之间的切向相互作用，其含义为：在接触面之间的剪应力达到某一临界剪应力值之前，切向运动一直保持为零，即处于粘结状态；直到接触面之间的剪应力等于临界剪应力值时，接触面之间才会发生相对滑动，见图2。临界剪应力值取决于法向接触力，其表达式为：

τcrit=μp

(1)

式中：μ是摩擦系数；p是接触面之间的接触压力。

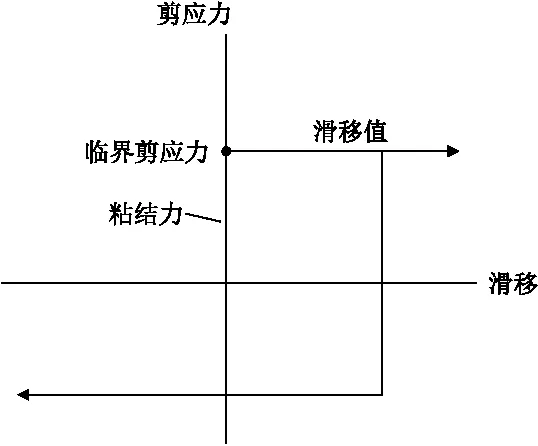
图2 摩擦行为

2.2 接触问题中的Hamilton原理

对于一般动力学问题，假定系统在边界Sσ上给定面力和位移边界Ti、Su，在时段[t1,t2]上，其总势能可表示为：

(2)

其中A(εij)是应变能密度。汉密尔顿原理可为上述泛函取驻值，即δΠ=0的位移场为真实位移场并可以同时满足初始位移条件、位移边界条件和域内几何方程。在动接触问题中则采用修正汉密尔顿原理，通过真实位移场令的泛函取驻值：

(3)

其中Sc表示接触边界，λ是拉格朗日乘子，G=0为接触条件。

3 羊曲水电站进水塔动力响应分析

3.1 工程概况

羊曲水电站进水塔为岸塔式，进水口为三向收缩型进水口，底板高程2640.0 m，顶唇轮廓线为椭圆曲线，其方程为x2/92+y2/32=1，进水口两侧采用半径为2.0 m的半圆曲线。进水塔塔顶高程2721.00 m，底板厚5.0 m，塔宽18.0 m，塔高86 m，顺水流方向长度15.0 m。

3.2 有限元模型和材料

采用ANSYS有限元软件对进水塔及其周围地基、岩体和回填混凝土建立模型并进行网格划分，并采用动力时程分析法进行动力接触分析计算。

(1)模型尺寸

塔体：取塔体底板至塔顶，共86 m；地基，宽度，塔的左岸、右岸各取28 m；塔前后各取40 m。深度：取接近于塔体高度的一倍：80 m。围岩：按照地基宽度取28 m。

(2)材料参数

进水塔上部采用C25混凝土，下部采用C30混凝土，回填混凝土采用C20。各材料参数见表1。

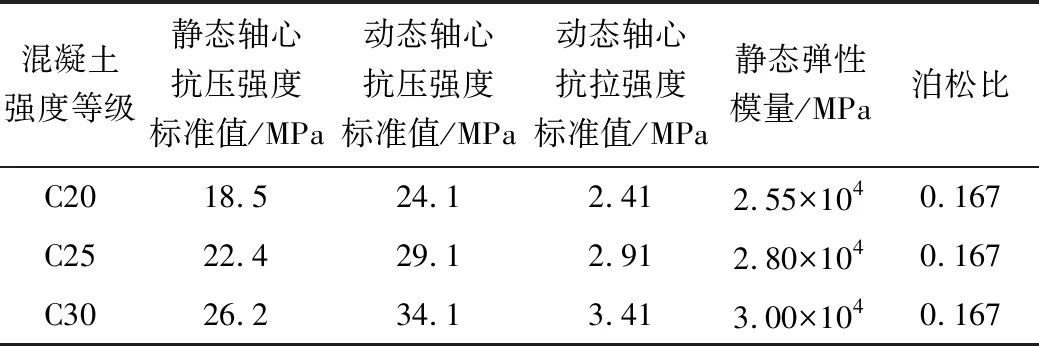
表1 材料参数

(3)模型单元

进水塔、地基、围岩和回填混凝土采用三维实体单元，均采用六面体划分。采用附加质量单元考虑动水压力作用。

在进水塔与回填混凝土交界面上设置面接触单元。目标面：与塔后回填混凝土相接触的面。接触面：塔后回填混凝土外表面。接触面与目标面的实常数：接触单元和目标单元形状均为矩形，初始接触状态由施加静力荷载计算并提取位移结果的应变状态作为初始接触状态。本文为未接触状态；静摩擦系数0.6，动摩擦系数0.55，摩擦类型为库伦摩擦。

有限元分析模型中坐标系采用直角坐标系，X正方向指向进水塔的进水向(顺水流方向)；Y正方向指向进水塔的左侧水平向；Z正方向竖直指向塔顶方向。

模型单元总数12062个,节点总数11335个；其中塔体单元数4860个；回填混凝土单元数730个；地基和围岩3248个；质量单元2948个。

塔体、地基、回填混凝土及围岩有限元模型见图3。

图3 进水塔动力分析有限元模型

3.3 荷载

计算时考虑了进水塔自重、扬压力、风荷载、地震荷载等动静力荷载。工程场地峰值加速度为0.304g，根据水工标准反应谱生成3条人工地震动记录进行三向加载。

4 结果分析

4.1 位移结果

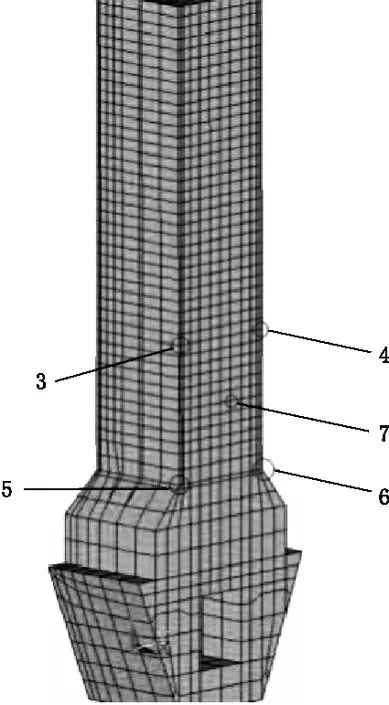
图4 塔体和塔后回填混凝土作用处关键点示意图

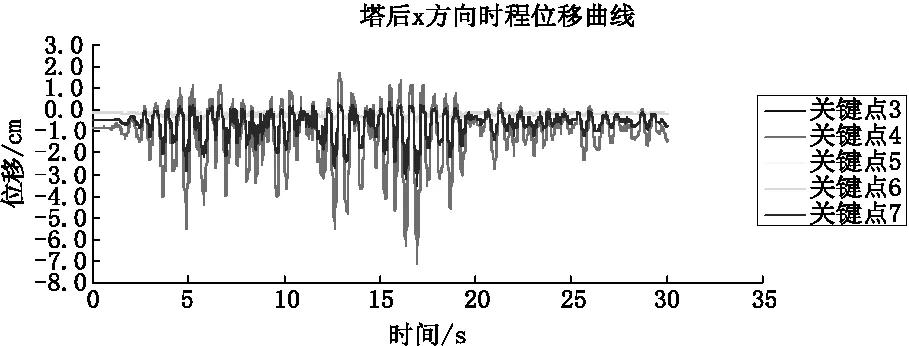
(a)关键点3、4、5、6、7顺水流方向时程位移曲线Ux

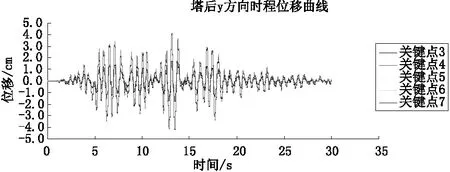
(b)关键点3、4、5、6、7垂直水流方向时程位移曲线Uy

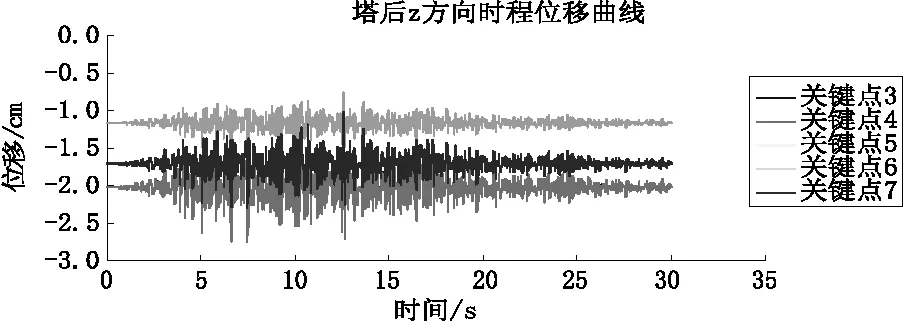
(c)关键点3、4、5、6、7竖向时程位移曲线Uz

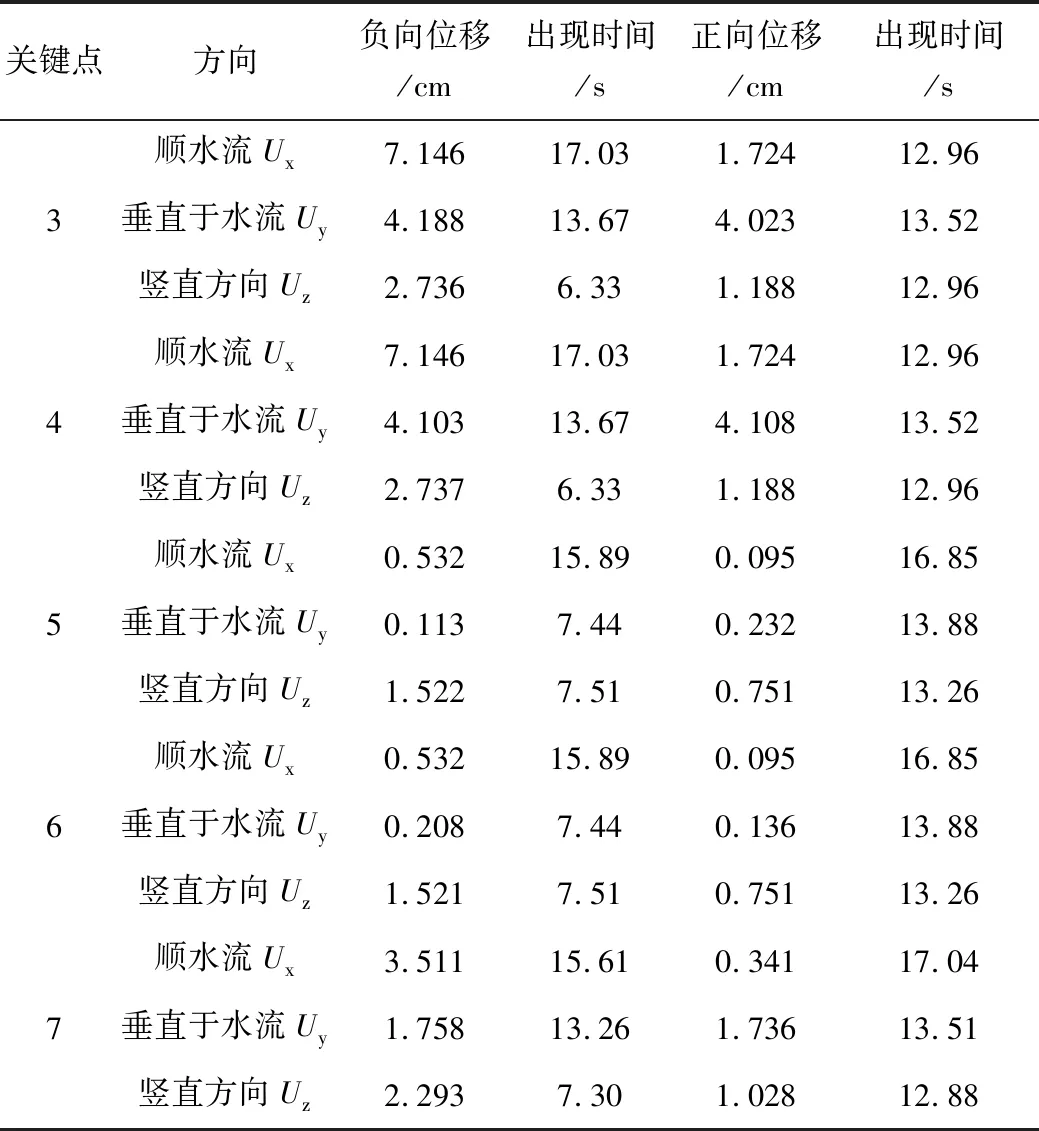
表2 塔体接触面上的关键点位移极值和出现时间表

由表2和图4得知：进水塔在地震作用下的不同时间节点、不同部位的位移矢量均有所不同，从纵向上来看，随着研究节点在塔体部位的增高，其位移也逐渐增加，说明塔后回填材料对塔体的约束能力随着塔体部位的增加而减弱；横向上分析，塔体与塔后回填材料的相对位置关系呈现一定的规律：两者相向位置值较小，背离位移值较大。说明在引入接触单元并运用非线性时程分析法后，塔体和塔后回填材料在地震动力作用下会发生嵌入(嵌入情况实际上与混凝土力学特性有关，嵌入值较大会造成该处结构的压碎和破坏，此种情况不在本文研究对象中)、张开和滑移现象。而拟静力法、线弹性模型均无法得出类似的结论，而实际工程中却是真实发生的。由此可见，文中研究所采用的方法得出的结论与实际工程所遇工况更加吻合。

4.2 应力结果

结构或构件受到外力会产生压应力或拉应力，当材料承受的外力超过所能承受的极限时会发生变形、扭转或断裂，在工程设计上必须避免结构应力状态大于正常使用极限并保留一定的安全度。在结构各种应力当中，最大拉应力和最大压应力是主要研究对象。本文提取的进水塔最大应力值见表3。

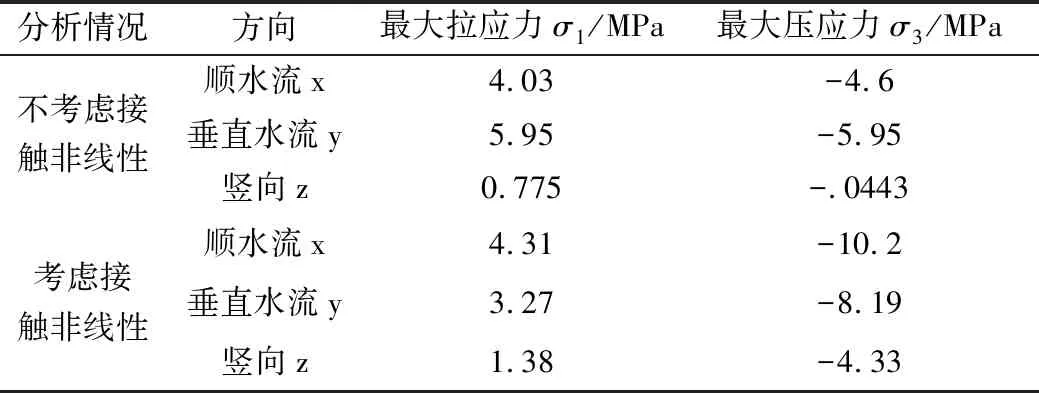
表3 不同方向塔体应力极值

仅考虑非线性边界条件下，整个模型(包括塔体、塔后材料、围岩)作为整体研究对象，塔体与塔后回填材料接触面视为整体变刚度，易产生应力集中现象。地震力作用下，塔体可能会发生明显的前、后摆现象从而使二者之间产生较大的拉应力、压应力，水平方向最大拉应力、最大压应力发生在塔背和回填混凝土交界面处(高程Z=40 m)。

而在接触非线性边界条件下，由于接触单元的特性，接触面上的抗压能力远大于抗拉能力，而在地震力的作用下，当应力值达到抗拉极限值后，接触面被拉开，塔后在Y方向的法相约束力消失，而后的震动过程中，接触面上只受压而不受拉，使得塔体的前倾趋势更加明显，同时塔后应力集中部位发生下移，从高程Z=40 m(塔后材料上边界)处下移至Z=23 m处(塔后材料下边界)。

通过以上数据总结可知，进水塔结构在借口突变部位易产生应力集中现象，这些位置都处于抗震的薄弱部位，在结构设计中应加强结构优化。

5 结论

本文采用有限元方法，研究了在考虑接触非线性条件下的塔体在地震作用下的结构物理力学变化规律，研究结果表明，在引入接触非线性单元后，塔体的主要研究指标(位移、部位、应力)均呈一定规律性变化，并且较不考虑接触单元时对结构的不利影响更明显。其条件设定、模拟过程、计算结果都与工程实际更加拟合，故在实际工程设计中考虑接触非线性是十分必要的。