一类带权微分系统特征值的研究
2021-04-12吴平
吴 平
(苏州职业大学 数理部,江苏 苏州 215004)
1 问题的提出
参考文献[1]、[2]提出了一类带权微分系统,见式(1),研究其第n个特征值和第n+1个特征值的关系。设(a,b)⊂R是一个有界区间,考虑
(1)
的特征值的关系,其中a 其中u1、u2、v1、v2为正常数。 根据方程理论知,式(1)的特征值是离散的,且都是正实数。 把式(1)写成矩阵形式,设 式(1)就可写成如下形式 (4) 显然,式(4)与式(1)是等价的。 设式(4)的特征值为 0≤λ1≤λ2≤…≤λn≤… 与之对应带权s(x)正交规范特征向量为Y1,Y2,…,Yn,…,即满足 (5) 根据式(3)和式(5),得 (6) 根据分部积分法,得 (7) 根据式(2)和式(7),得 (8) 设 其中 φi与Yj带权s(x)正交(i,j=1,2,…,n), 且Dkφi(a)=Dkφi(b)=0(k=0,1,2,3,i=1,2,…,n)。 于是,利用Rayleigh定理,得到下列不等式 (9) A(-D)(P(x)(A(D)φi)) (10) (11) 设 根据式(11),得 (12) 根据式(9)和式(12),有 (13) 用λn替代式(13)中的λi,成立有 (14) 为了证明一类带权微分系统(1)第n个特征值和第n+1个特征值的关系,需要先证明下列引理,在证明中参考了文献[3]、[4]中的引理及证明的内容。 引理1 设Yi是式(4)对应特征值λi的特征向量,则 证明 由式(8),得 (15) 根据分部积分法、Schwartz不等式、式(6)和式(8),得 (16) 化简,得 (17) 由式(8)及式(17),得 (18) 根据式(16)和式(18),有 (19) 根据式(15)和式(19),即得引理1。 引理2 设λ1,λ2,…,λn是问题(4)的n个特征值,则 证明 根据分部积分法和φi的定义,得 (20) 根据式(20),有 (21) 根据式(2)和式(6),得 (22) 根据式(2),式(18)和式(8),得 (23) 根据式(2)、分部积分法、Schwartz不等式,式(8)和式(18),得 (24) 根据式(21),式(22),式(23)和式(24),即得引理2。 引理3 对于φi和λi(i=1,2,…,n), 则 (25) 证明 根据φi的定义,得 (26) 根据分部积分法,有 (27) 根据式(26),式(27)和式(6),有 根据Schwartz不等式和引理1,有 。 引理3得证。 参考文献[5]、[6]中的定理及证明的内容,以及利用引理1、引理2、引理3和Young不等式,得到并证明了一类带权微分系统(1)第n个特征值和第n+1个特征值的关系,即定理1和定理2。 定理1 如果λi(i=1,2,…,n+1)是式(5)、式(6)的特征值,则 证明 根据引理3,成立着 再由式(14)和引理2,可得定理1①,在定理1的①中用λn替代λi,可得定理1的②。 定理2 对于n≥1,则 证明 选择参数σ>λn,由式(13),得 (28) (29) 其中δ>0为待定常数。 根据式(28)、式(29)、式(3)和引理1,化简得 (λn+1-σ)V+T≤I (30) (31) 为了使(31)式右端的值达到最小,取 (32) 将式(32)代入式(31),有 (33) 根据引理2、式(30)和式(33),得 (34) 其中σ>λn,选择σ使(34)式右端等于零,即 (35) 设 (36) 易知,f(σ)是在(λn+∞)内单调减少的连续函数,其值域为(0,+∞),因此,存在唯一的σ使等式(35)成立。从(34)式知σ≥λn+1,用λn+1来替代等式中σ, 即得定理2。 方程的特征值问题是数学学科研究的一个重要领域,涉及的内容复杂而广泛。本文研究了一类带权微分系统特征值的关系,并获得了第n个特征值和第n+1个特征值的关系:定理1和定理2。其结果在实际中应用广泛,如在物理学和力学等领域。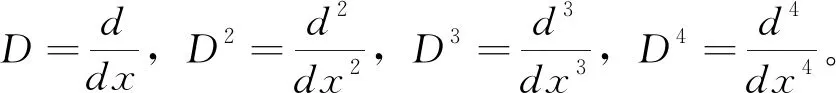
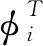
2 主要引理
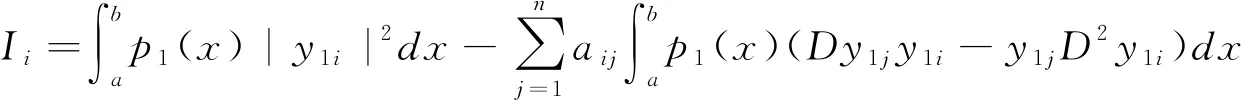
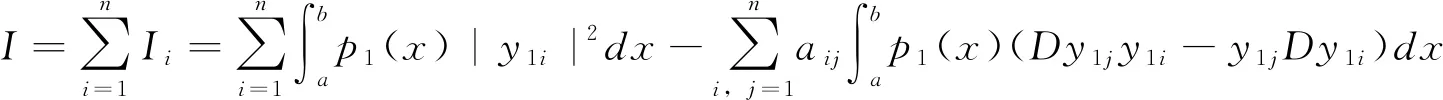
3 主要结论
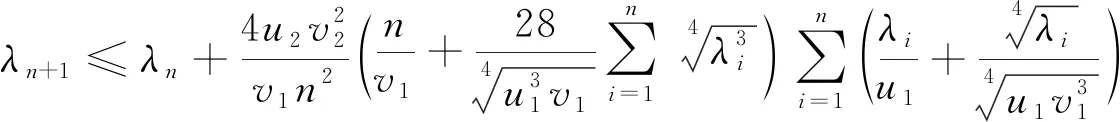
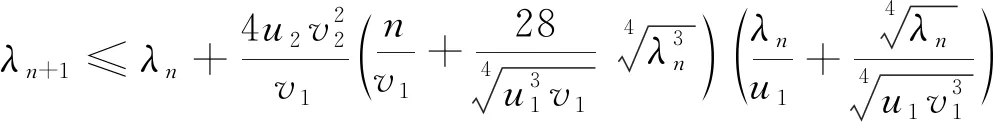
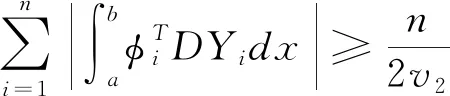

4 结 论
