一种具有强抗噪性的深度学习故障诊断模型
2021-04-12吴春志吴守军冯辅周朱俊臻
吴春志,吴守军,冯辅周,朱俊臻
(陆军装甲兵学院车辆工程系,100072,北京)
旋转机械是指主要依靠旋转动作完成特定功能的机械,典型的旋转机械有齿轮箱、减速机、汽轮机、燃气轮机、风机、发电机、发动机等。以齿轮箱为例,作为传动系统的关键部件,其广泛应用于风力发电机组、煤矿开采设备、车辆传动机构等很多重要的机械设备。齿轮箱故障可能会造成生产停滞,甚至导致人员伤亡[1]。齿轮箱的主要故障有不平衡、轴承不对中、松动及齿轮部件的断裂磨损等[2-3]。因此,对旋转机械进行在线监测与故障诊断成为系统设计和维护中非常关键的环节[4-5]。
在齿轮箱的实际工作中,运行工况多变,在实际工作中采集齿轮箱的振动信号,远比台架试验中得到的信号受噪声干扰严重[6]。但是,由于条件有限,在实际应用环境中得到特定故障信号有一定的难度,因此由人为在台架试验中注入故障是进行不同故障模式信号收集、建立故障诊断模型最直接有效的手段[7]。如何平衡台架试验与实际环境应用间的矛盾,是摆在故障诊断模型进一步应用的难题。
深度学习是近年来人工智能领域研究的热点,作为代表的卷积神经网络以其特有的网络结构和训练方式,直接以原始信号作为输入,模拟输入和输出之间的复杂关系,减少了对专家经验的依赖,也无需人工提取特征,在旋转机械故障诊断中应用也越来越广泛[8-11]。但是,传统的深度学习模型鲁棒性差,诊断准确率易受噪声影响,为此,一些学者从数据和算法两个方面,提出了对噪声有一定抵抗能力的深度学习故障诊断模型。文献[12]使用自编码器先对信号降噪再输入到一维卷积神经网络(1-DCNN)模型中实现降噪,但需要训练两个模型,而且测试信号的信噪比仅为1 dB。文献[13-16]提出了具有一定抗噪性的深度学习模型,可以不对数据进行处理,但是,测试信号的信噪比最低仅为0 dB,对低于0 dB的强噪声干扰没有研究或者诊断效果较差。
本文在文献[17]改进的1-DCNN模型基础上引入多尺度的概念,提出多尺度卷积神经网络(MSCNN)模型。该模型可以降低训练集信号间隔的敏感度,提高诊断的准确率[18]。同时提出一种高幅值截断(HAT)的频谱信号处理方法,处理后的频谱信号作为训练集训练MSCNN模型,然后在不同的信噪比测试集中进行测试。将本文模型与集合经验模态分解(EEMD)降噪方法、直接以振动信号和频谱信号作为输入的MSCNN模型以及使用1-DCNN模型的方法进行对比,以不同信噪比测试集中的精确率和召回率的调和平均值为评价指标,采用具有丰富故障模式的PHM2009齿轮箱故障数据集在强噪声干扰下进行测试,验证本文模型的抗噪能力,同时使用加权梯度类激活映射(Grad-CAM)方法可视化显示模型的分类权重。
1 MSCNN模型
将传统用于二维图像识别的卷积神经网络模型改造成用于一维信号的1-DCNN,如图1所示。一个完整的CNN模型包括了输入层、CNN层组(由卷积层和池化层组成)、全连接层、输出层等几个部分。

图1 1-DCNN网络结构图
为了提高特征提取的维度,将多尺度的概念引入1-DCNN中,即增加多种步长移动方式,以提取信号不同尺度的特征,扩充特征维度,得到MSCNN模型,如图2所示。其中,convd1、convd2、convd3分别代表移动步长为1、2、3的卷积核。不同的CNN层组搭配不同移动步长的卷积核,可以使卷积后得到不同尺度的特征量。不同尺度的特征之间差异性相对较大,这增加了特征提取的丰富程度。

图2 多尺度卷积神经网络模型
2 Grad-CAM方法
在网络进行全连接之前,卷积层保留了丢失的空间信息,Grad-CAM方法[19]可利用最后一层卷积层的梯度信息,然后将信息反向传播到其他卷积层,以此来了解该卷积中每个特征图对特定分类做出决策的重要性,即权重。将卷积层的特征图与其对应的重要性权重相乘后,就得到了所分类的特征定位图。与CAM方法不同,Grad-CAM方法不需要将网络修改为平均池化重新训练,对于含有全连接层的一般网络可直接使用,具体可分为以下6个步骤。
(1)假设Lc,Grad-CAM∈cu×v是类别c的定位图,其中u和v是其宽度和高度。
(2)在输出层之前计算类别c的梯度yc。

(4)分别对Q个特征图的梯度求像素平均,获得该特征图的重要性权重,计算公式如下
(1)
式中:αc,q为第q个特征图对类别c决策的重要性;Z为Aq的像素数;Aq(i,j)为Aq中(i,j)处的像素值。
(5)将Q个特征图与其对应的权重αc,q相乘再求和就得到了Lc,Grad-CAM。对类别c有正向贡献的特征值应该被关注,而负向贡献的应该舍弃,因此增加一个修正线性单元(ReLU)作为激活函数,将小于0的特征值置0,由此可得
(2)
(6)将得到的Lc,Grad-CAM重采样,匹配输入的样本大小,即可得到网络对样本的分类权重定位图。
3 测试集构建
本文以PHM2009 Challenge Data数据库的斜齿轮故障为例进行分析。该数据集是PHM协会在2009年国际竞赛的全套齿轮箱数据。斜齿轮箱结构如图3所示。斜齿轮啮合模式下共有8种包含齿轮裂纹、断齿,轴承滚动体、内圈、外圈以及轴的不平衡、键槽磨损等单一及复合故障模式(Spur1~Spur8)[20]。采样频率为66.67 kHz,采样时间为4 s,采样点数为266 656。为了优化模型的运算速度,在有限数据样本内包含更多周期的信号,对原信号进行降采样1/3处理。取样本数据段长度为1 600点,可以包含2~3个周期的振动数据。

图3 PHM 2009 Challenge Data斜齿轮箱结构
齿轮箱在试验中测得的振动信号本身就包含一定的噪声,并不是纯净的故障模式振动信号,但是相对于实际应用情况,试验台得到的信号信噪比相对较高,因此为了模拟实际工作中可能遇到的噪声情况,在信号中添加不同信噪比的高斯白噪声。
信噪比RSN的定义如下
(3)
式中:Psingal和Pnoise分别代表信号和噪声的有效功率;Asignal为信号的平均幅值;Anoise为噪声平均幅值。信噪比的单位为dB。为了更好地显示噪声对信号的影响,列出信号幅值与噪声幅值的比值Asignal/Anoise,该比值与信噪比的关系如表1所示。
为了更直观的展示不同信噪比的含噪信号,以Spur2信号为例,图4显示出不同信号比下含噪信号、噪声信号以及含噪信号的频谱。结合表1和图4可知,当信噪比为0 dB时,噪声信号和原信号的幅值比为1∶1,此时频谱图还能基本保未加噪声时的形状(如图4c所示),但当信噪比继续减小,尤其是减小到-10 dB时,噪声幅值已经是原信号的3倍(如图4h所示),频谱图中已经看不到原信号大概形状,低幅值的频率都湮没在噪声中。因此,若使提出的抗噪模型有效果,则至少应满足在0 dB时保持较高的诊断精确率。

表1 信号噪声幅值比与信噪比关系
在时域中进行降噪处理很难完全将加入的噪声分量剔除出去,由图4可知,在信噪比取一定范围内,含噪信号的频谱图整体趋势是不变的。如果将幅值小于某一定值的频率直接置0,只考虑幅值较大的几个频率值,将调整后的频谱信号作为输入,将在一定程度上减弱噪声的影响。以PHM2009齿轮箱的正常信号Spur1(35 Hz转速下低负载)为例进行分析。

(a)RSN=0 dB含噪信号
图5是进行HAT处理的流程,在求取频谱后,按照幅值从大到小的顺序排列,然后取前k个为有效值,第k个值为α,然后将小于α的值置0,得到最终的HAT频谱向量(该频谱向量的长度为原样本经过求取频谱后再经HAT处理后的数据点数,用符号N表示)。通过实验发现,k值过大起不到降噪效果,过小会影响样本的有效数据量。在本次研究中k值统一取30,整个数据集α的确定以正常信号下第30个频率值的平均幅值为准,本数据集中α为0.029。采用HAT处理数据集后,减弱了频谱中幅值低的频率成分对分类的权重贡献,减少低幅值噪声信号对信号的干扰,但是依然保留了0值所在的位置信息。降低了加噪信号和原信号之间的差异,突出高幅值频率成分的权重贡献。

图5 HAT处理频谱信号流程
Spur1在加入不同信噪比噪声数据后进行HAT转换可得到图6,可以看出在信噪比为0 dB时,数据结构变化不大,但是当信噪比继续增大到-5 dB甚至-10 dB时,HAT后的数据也几乎湮没在噪声信号里。HAT转换后的频谱不止是特征数值上的信息,还包括了特征的位置信息。

(a)RSN=5 dB
4 算例分析
本节中采用未作处理的直接以振动信号进行输入的Raw-MSCNN模型、经过EEMD降噪的振动信号作为输入的EEMD-MSCNN模型、以原始频谱信号作为输入的Frequency-MSCNN模型和本文提出的HAT-MSCNN模型以及作为对比的HAT-CNN模型(在后续图表中省略MSCNN和NN),在试验台取得的振动信号组成的训练集中进行训练,在添加不同信噪比高斯白噪声的测试集中进行测试,对PHM2009齿轮箱故障数据做故障诊断研究,具体流程如图7所示。
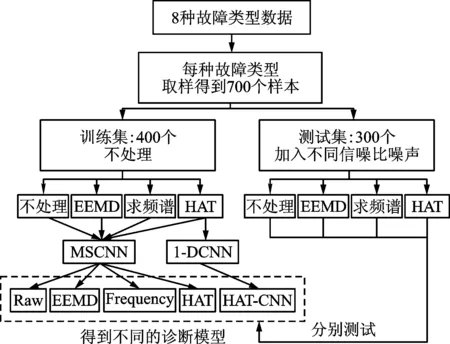
图7 5种模型训练和测试的流程图
在Raw-MSCNN和EEMD-MSCNN模型中,输入数据都是基于时域信号,样本长度为1 600点,为了保证模型的一致性,在应用Frequency-MSCNN、HAT-MSCNN和HAT-CNN时取样本长度为3 200点,然后求得频谱信号长度为1 600点,测试集信噪比与表1设置一致。两种深度学习网络卷积核大小都设置为21和11,学习率为5×10-4。1-DCNN两个层组的卷积核数量为8和15,MSCNN为6和10,这样在全连接层的神经元数量都为6 000,保证了特征提取数量的一致。
抗噪模型至少应在信噪比为0 dB时保持较高的诊断精确率。因此本文采用t分布领域嵌入算法(t-SNE)分析在RSN=0 dB时,测试集样本在不同模型下全连接层的聚类效果,得到图8。其中t-SNE的参数设置为PCA模式,最大迭代次数10 000,学习率为500。
t-SNE关心的是学习维持数据的局部结构,降到2维空间时会保留数据的流形结构,类间的距离远近不代表真实数据的分类距离,是一个聚类示意图。由图8可知,HAT-MSCNN和Freuqency-MSCNN在信噪比为0 dB时分类效果最好,其他模型在聚类过程中都有重叠,分类效果较差。

(a)RAW (b)EEMD (c)Frequency
由于在增加了高斯白噪声后,模型的诊断的精确率和召回率偏差较大,因此本节采用二者的调和平均值F作为评价指标,其计算方法如下
(4)
式中:参数β一般取1;Precall是召回率;Pprecision是精确率。
表2比较了几种模型在不同信噪比噪声信号中的F值,由表2可知,HAT-MSCNN和Frequency-MSCNN相较于其他几种模型,在较强噪声干扰(RSN=-4 dB)时仍能保持较高的诊断性能。当信噪比较低时,尤其是HAT-MSCNN,在RSN=-6 dB时,F值达到了89.1%,在RSN≥-4 dB时,F值超过了98%。HAT-CNN模型在RSN≤-4 dB时无法分类故障,说明1-DCNN对数据加噪敏感。因此,在强噪声环境下,HAT-MSCNN具有更高的抗噪性和故障特征学习能力。

表2 几种模型在不同信噪比噪声信号中的F值比较
使用Grad-CAM方法得到的本文模型对不同故障类型分类权重的可视化结果如图9所示。图9表明,本文模型对不同故障类型关注的侧重点不同,幅值较高的特征部分更加突出,减少了可能会被噪声影响的幅值较低的频率成分对分类的干扰。

(a)Spur1 (b)Spur2
图10是本文模型对Spur5不同信噪比的测试信号的分类权重,结合图9e可知,本文模型对于分类成Spur5的故障模式,更加关注其250点和800点左右的成分,这两个点附近对应的频率在频谱中幅值占比较高。在不同信噪比的噪声信号中,本文模型准确地找到了这两个频率段的特征。
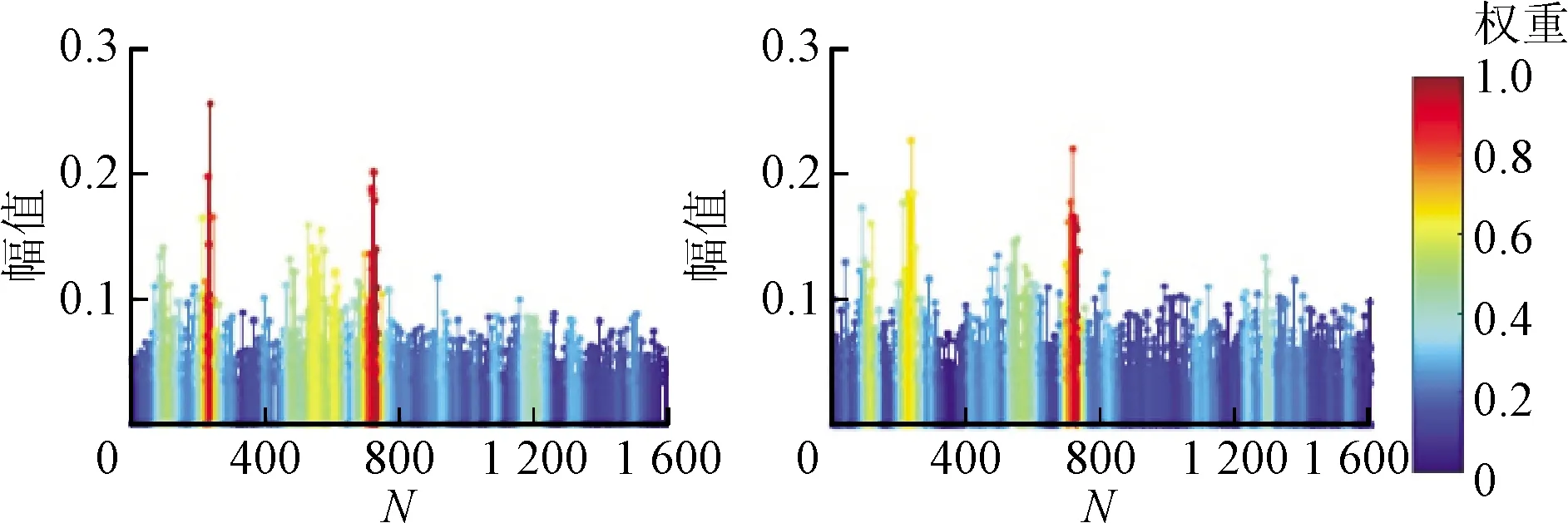
(a)RSN=0 dB (b)RSN=-2 dB
5 结 论
本文提出一种强抗噪性的故障诊断模型HAT-MSCNN,实现了在强噪声干扰下齿轮箱多种复合故障的诊断识别。首先使用高幅值截断的策略构建训练集,然后输入到多尺度卷积神经网络模型进行故障诊断,同时使用Grad-CAM方法可视化显示分类权重。经HAT处理后的信号突出了幅值较高的频率成分,降低了低幅值频率成分被噪声耦合后对模型诊断的影响。实验结果表明,直接以频谱信号作为输入的诊断模型虽对噪声有一定的抵抗能力,但HAT-MSCNN模型在信噪比为-4 dB时,诊断准确率为98.6%,而在信噪比为-6 dB时,诊断准确率依然能保持在90%左右,远高于其他模型。因此,HAT-MSCNN模型可以有效减少噪声对诊断模型的影响。
