面向误差传递的复杂机械产品装配单元划分方法
2021-04-12张嘉锟陈琨于慧李丽丽高建民高智勇
张嘉锟,陈琨,于慧,李丽丽,高建民,高智勇
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
装配是产品制造中的最后一个阶段,也是产品研制过程的关键环节。据统计,与装配相关的工作量平均占据整个产品研制工作量的45%,在很大程度上影响着产品的成本和最终质量[1]。产品装配的根本问题之一是保证装配精度[2]。在装配阶段,对影响产品装配精度的零件误差源和误差传递进行分析,对产品装配精度和一次装配成功率的提高具有重要作用[3],对提高产品装配效率及最终产品质量具有重要意义。
国内外学者对装配误差传递进行了许多研究。Hu等提出误差流理论(stream of variation,SOV)[4],目前被广泛应用于加工过程[5]和装配过程[6]的误差建模与分析。此外,一些学者引入状态空间模型,为装配误差流的控制奠定了理论基础[7-8]。另一方面,Liu等基于复杂网络理论构建了零件加工误差传递网络,为误差传递建模与分析提供了全新的思路[9];祝鹏等通过引入复杂网络的相关理论与方法,解决了多阶段装配系统的误差建模与关键装配特征识别等问题[10]。然而,基于误差流和状态空间模型的方法需要采集大量数据,并且需要不断进行坐标转换,计算复杂度较高,且会在一定程度上造成严重的数据失真;基于复杂网络的方法虽然在一定程度上简化了误差建模与分析难度,但随着零部件的增多,装配特征也会急剧增长,为模型的建立与分析带来挑战。综上,对于零部件众多、零件间关联关系复杂的复杂机械产品来说,难以直接应用现有方法进行装配误差传递建模与分析。
对于复杂机械产品,直接对整个装配体进行相关研究一般比较困难,甚至无从下手。目前常用的方法是化繁为简,将复杂产品分解成相对简单的装配单元来研究,然后集成各个装配单元来讨论整个产品的特性。国内外针对装配单元划分的研究大多面向装配工艺规划,Wang等基于模糊层次分析法生成装配单元决策图,并采用最小生成树算法进行装配单元的划分[11]。靳江艳等以广义装配关系强度和装配并行度为目标建立优化模型,采用免疫克隆算法进行复杂产品的装配单元划分[12]。卢鹄等引入加权有向图,运用模糊聚类算法完成装配单元划分,并基于撕裂算法进行子装配单元的顺序规划[13]。邹成等利用灰色区间分析法计算零件间的工艺关联度,并通过归属决策图进一步确定其所属的装配单元[14]。Sheng等引入装配语义信息衡量数控机床装配关系的强弱,以此为依据进行子单元划分,并基于遗传算法实现各个子装配单元间的序列规划[15]。刘博等提出一种基于连接关系与间接关系相结合的装配关系强度计算方法,并利用模糊聚类分析法对船舶分段的组立结构进行了划分[16]。此外,李冬英等以动作为划分依据,提出元动作装配单元,并在元动作装配单元层次上建立了装配误差模型[17]。综上,研究对象的特点以及装配单元划分的出发点不同,采用的划分依据也都不同,现有方法存在以下不足:①同一个零件只能被划分到一个装配单元;②装配关系强度的衡量以专家打分法为主,主观性较强;③层次性较差,多数方法仅能得到一组划分结果;④针对装配误差传递的单元划分方法研究相对较少。
本文提出一种面向误差传递的复杂机械产品装配单元划分方法。首先根据产品装配工艺信息,考虑零件间的装配关系以及必要的测量关系,基于复杂网络理论构建零件层级关联网络;然后采用模糊层次分析法与专家打分法相结合的方式为零件间关联关系赋权,得到零件关联加权网络;最后基于改进的连边社团检测算法进行装配单元划分,并以某汽轮机低压模块为例对本文方法进行应用验证。
1 装配建模与单元划分方法
机械产品的最终质量是制造系统中各种误差或缺陷综合作用的结果。例如,零件自身在加工过程中产生的制造误差和装配过程中的工艺误差,都是以零件具体的特征为载体,随着装配过程的不断推进在零件间逐渐传递累积,进而导致最终产品的质量问题。对于复杂机械产品而言,其装配特征和装配工艺均十分复杂,需要保障的质量特性繁多,基于传统方法直接以特征为基础进行建模的难度较大,也会使后续的误差分析等工作较为棘手。
针对上述问题,本文基于化繁为简的思想,引入复杂网络理论,提出一种面向误差传递的复杂机械产品装配建模及单元划分方案,根据需要保证的质量特性,将复杂产品分解成相对简单的单元来研究,从而降低后续基于特征的建模及分析难度。
1.1 引入复杂网络
复杂网络是将系统中的组元映射为节点,组元之间的相互关系映射为边,研究系统中各要素相互关联作用的拓扑结构和动力学演变特征[18]。复杂网络可以定义为G={〈vi,vj〉,wij},其中vi、vj表示网络中的节点,wij为两节点连接的初始权重,若vi、vj之间存在连接关系,即两节点间具有连边,则wij=1,否则wij=0。此外,按照连边是否存在方向可将其分为有向网络和无向网络。
对于机械产品而言,复杂网络能够清晰地描绘出零部件及特征的拓扑结构和统计特性,可以反映出误差传递的强度和路径,符合误差流的传递特征,此外,复杂网络的社团特性符合面向误差传递的装配单元划分要求。因此,本文基于复杂网络理论建立装配模型并进行单元划分。
1.2 网络建模及单元划分方法
针对复杂机械产品直接从特征层面进行装配误差建模与分析困难的问题,本文提出一种双层结构装配模型,如图1所示。该模型体系共分为两层:装配零件层和装配特征层。从网络图的角度看,零件层是特征层建立的基础,零件层的拓扑结构决定了特征层的拓扑结构;特征层是零件层的投影,同时也是对零件层的误差信息补充。两个层级之间并不是简单的叠加关系,而是相互联系,共同搭建起面向复杂机械产品误差传递的分析平台。
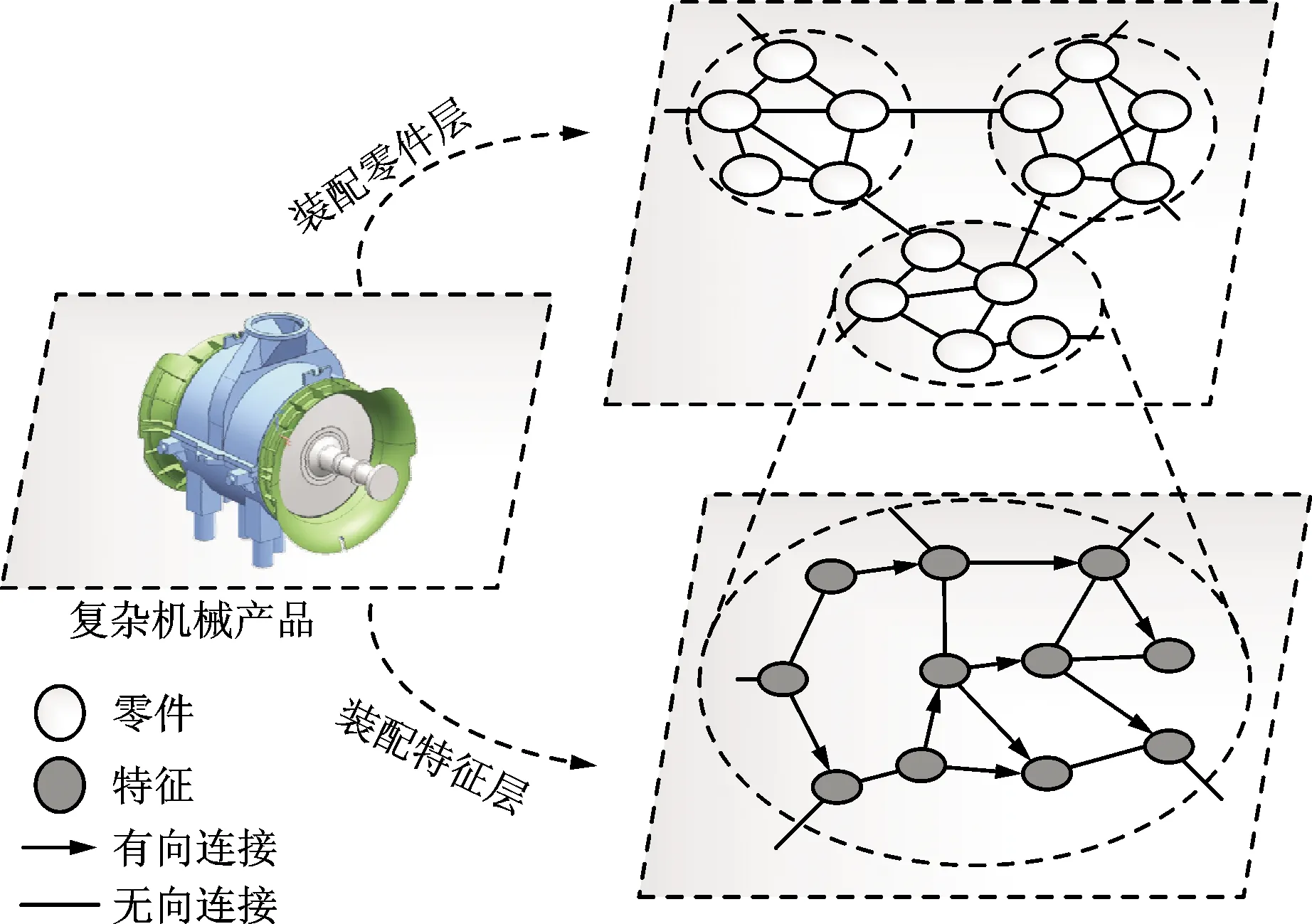
图1 面向误差传递的复杂机械产品装配建模方案
该模型建立的总体方案:首先在装配零件层级构建了关联网络;其次基于零件层级网络的社团特性进行装配单元划分;最后基于划分结果,以装配单元为基础,构建特征层级误差传递网络。本文主要讨论零件网络的构建及装配单元划分方法。
2 零件网络构建与装配单元划分
结合装配单元划分的需求,本文将零件层级关联网络定义为无向有权网。图2所示为本文提出的零件网络构建及装配单元划分过程,主要包括关联网络构建、关联网络赋权以及网络单元划分等内容。
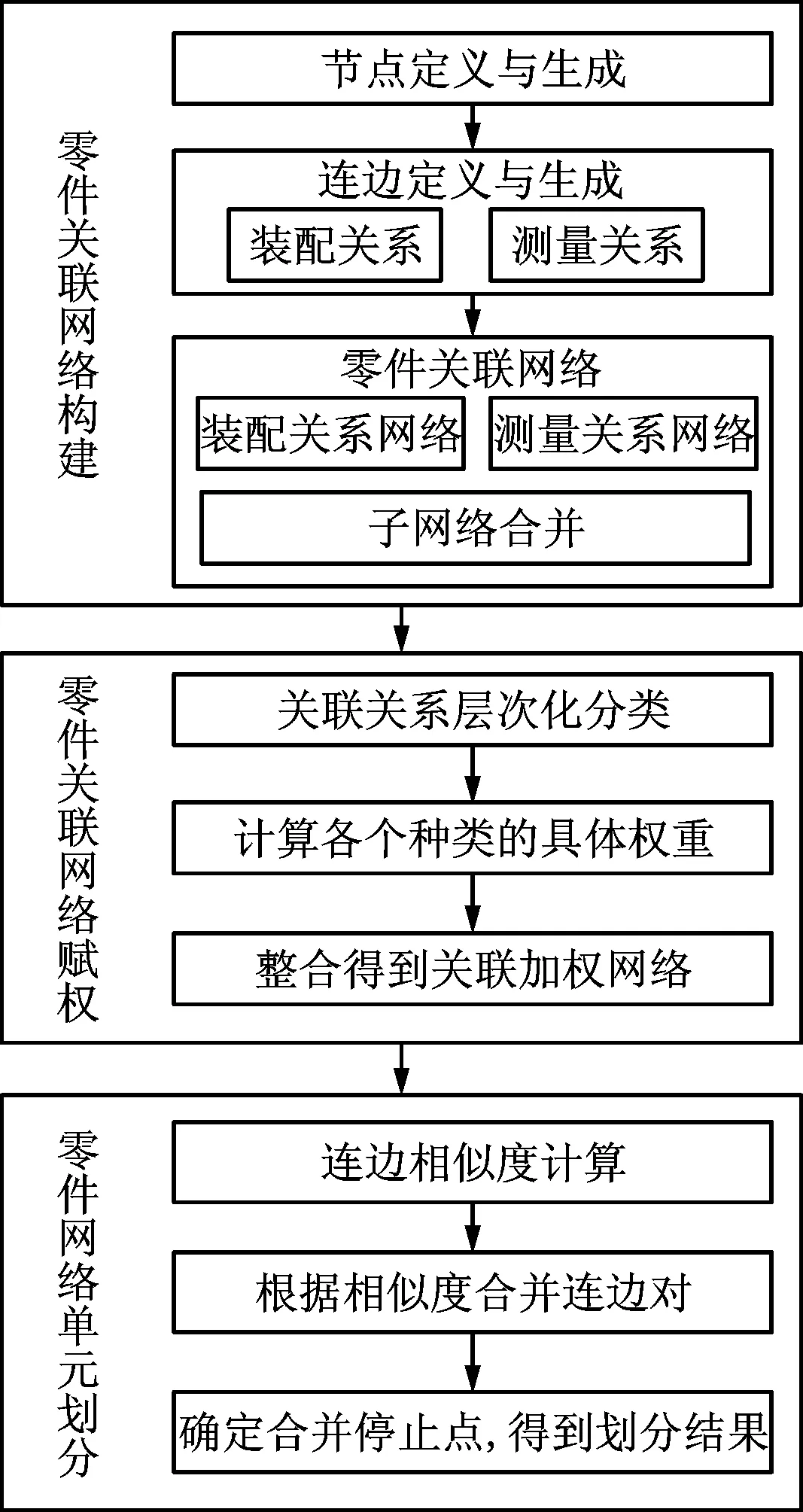
图2 零件层级网络模型构建及装配单元划分过程
2.1 零件层级关联网络的构建
现有文献在进行单元划分时大都仅考虑装配关系,然而对于复杂的机械产品,部分零件之间虽然不存在严格意义上的装配关系,但是却有着较强的关联。图3所示为某型号汽轮机部分结构,通流间隙是汽轮机需要保证的重要精度,以图中隔板通流间隙为例,它是由隔板汽封和转子两个零件形成的。从装配关系角度来看,隔板汽封与隔板下半通过悬挂销等零件与内缸装配在一起,转子与两侧的轴承以及轴承座装在一起,即隔板汽封和转子之间不是严格的装配关系。在实际工艺中,需要对隔板通流间隙进行测量,若不满足精度要求,会对隔板汽封和转子等零件进行微调,以保证最终的装配精度。本文将这种零件间特殊的关联关系定义为测量关系,并将其作为零件关联网络的组成部分,零件关联网络构建的具体步骤如下。
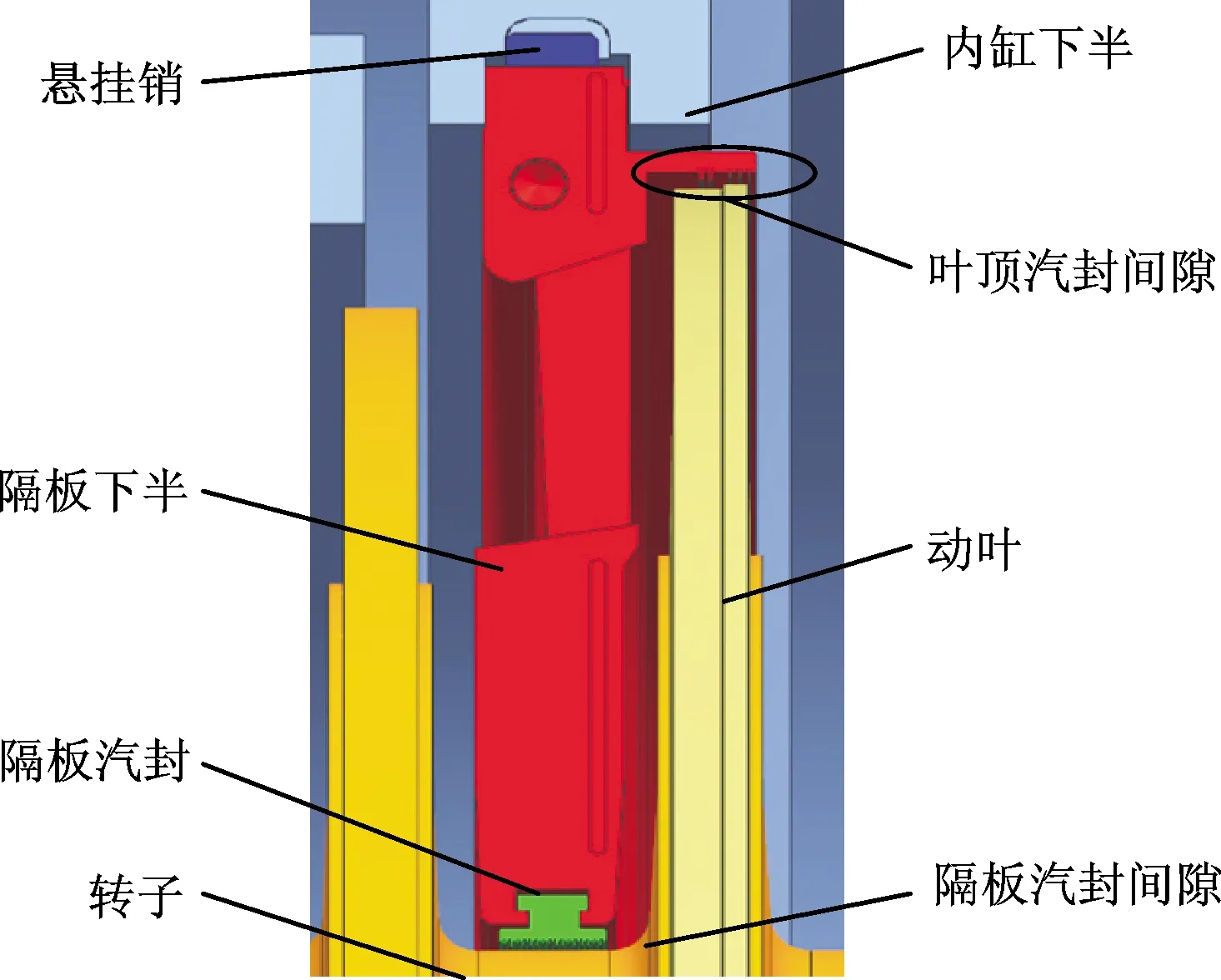
图3 某型号汽轮机部分结构
(1)零件装配关系网络的构建。根据复杂机械产品的装配工艺信息,获取零件列表,确定零件间的装配关系,如连接关系、几何约束、传动关系等。将产品中的零件映射为复杂网络中的节点,零件间的装配关系映射为网络的边,网络可描述为
GA=〈A,EA〉
(1)
式中:A={a1,a2,…,al}表示具有装配关系的零件节点集合,l表示具有装配关系的零件数量;EA={ea1,ea2,…,eah}表示具有装配关系的零件节点间的边集,h表示零件间装配关系的数量。
(2)零件测量关系网络的构建。根据装配工艺信息,对产品装配质量起重要影响的测量关系,以零件装配关系网络得到的零件节点为基础,将零件间的测量关系定义为网络的边,网络可描述为
GM=〈M,EM〉
(2)
式中:M={m1,m2,…,mu}表示具有测量关系的零件节点集合,u表示具有测量关系的零件数量;EM={em1,em2,…,emv}表示具有测量关系的零件节点间的边集,v表示零件间测量关系的数量。
(3)零件关联网络的合成。将零件装配关系网络和零件测量关系网络进行合并,即对网络GA和GM进行合并,可得复杂机械产品零件关联网络
G=〈V,E〉=GA∪GM=〈A,EA〉∪〈M,EM〉
(3)
式中:网络节点集V={a1∪…∪al∪m1∪…∪mu};边集E={e1,e2,…,eg},g为复杂机械产品零件关联网络总边数。
若仅考虑零件装配关系,则零件装配关系网络GA即为最终的零件关联网络G。
2.2 零件层级关联网络的赋权
为了进一步衡量零件间关联关系的强弱,需要对零件关联网络进行赋权。现有文献在衡量关联关系强度时多采用专家打分法,对于复杂机械产品而言,零件之间的关联关系种类较多,基于专家打分法容易出现评价思维不一致等问题,而且具有较强的主观性,结果会有较大偏差。因此,本文提出模糊层次分析法(FAHP)[19]与专家打分法相结合的方式,计算零件间关联关系的权重。
FAHP是在传统层次分析法的基础上引入模糊集理论,是一种定性与定量相结合的系统分析方法,当某一层次的评价指标很多时(如4个以上),能有效提高结果的客观性;当某一层次的评价指标很少时(如仅有2个),采用专家打分法能更好地体现专家的经验,直观性强。本文的具体加权步骤如下。
(1)根据2.1节所得零件关联网络G的边集E对零件间关联关系进行层次化分类。如图4所示,可将零件间关联关系首先分为装配关系和测量关系,其次分别对两类关系进行更为细致的划分,具体划分应结合实际产品的特点进行。

图4 零件间关联关系层次化分类
(2)判断各层次含有种类的数量,若该层次的种类较少(4个以下)时,采用专家打分法获取各个种类的具体分值,并保证该层级各种类的最终分值和为1,即对分值做如下处理
(4)
式中:zα为种类α在该层次的最终权值;t为该层次关联关系种类总数(t<4);sα为种类α的原始分值。
(3)对于其余层次(种类不少于4个),基于FAHP文献[20]的方法进行权重计算,过程如下。
步骤1 构建模糊互补矩阵,参考专家意见,对该层次中的各个种类进行两两比较,用cop表示种类o相对种类p的重要程度,则模糊互补矩阵表示为
(5)
式中:coo=cpp=0.5,且cop+cpo=1(o,p=1,2,…,q);q为某一层次所含种类数量;cop按表1确定。
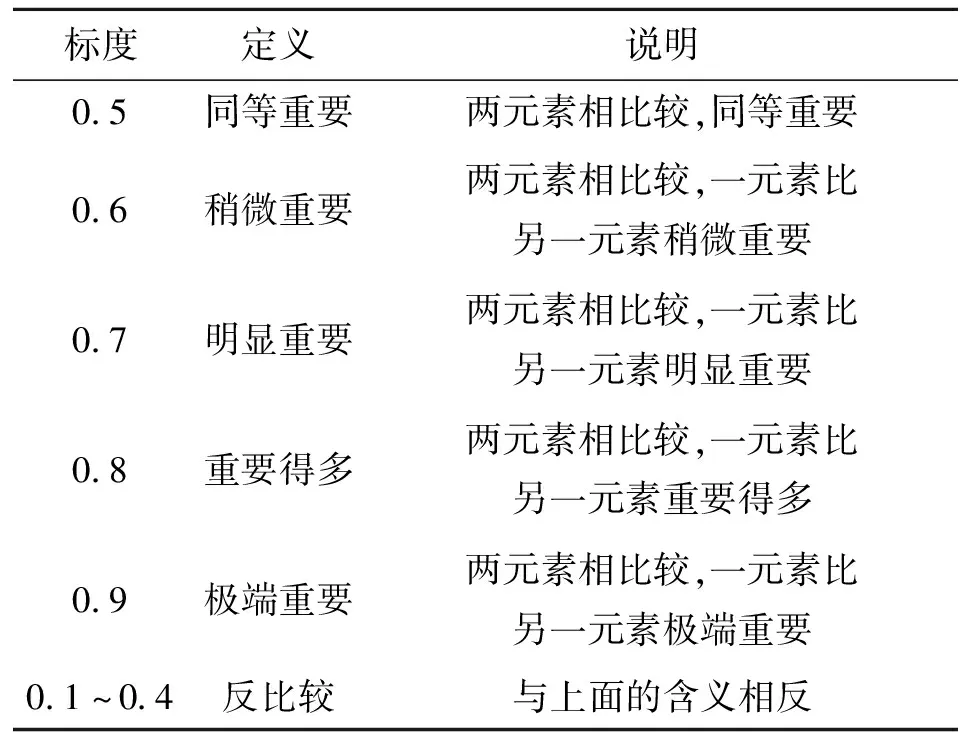
表1 模糊互补判断规则
步骤2 将模糊互补矩阵转化为模糊一致矩阵,对式(5)按行求和,可表示为
(6)
进行如下变换,得
rop=(ro-rp)/(2q)+0.5
(7)
由此得到的矩阵R=(rop)q×q即为模糊一致矩阵。
步骤3 使用方根法计算各层次各个种类特征的权重,计算公式如下
(8)
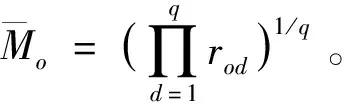
(4)根据式(4)(8)的计算结果,整理得到各个种类的具体权重,用W={w1,w2,…,wg}表示权重集,与2.1节所得零件关联网络进行整合,则零件层级的关联加权网络模型可表示为
GW=〈V,E,W〉
(9)
2.3 零件层级装配单元划分
面向误差传递的装配单元划分的本质是根据零件之间的关联关系将整个装配体分解成若干个单元,使得属于一个单元的零件间联系相对紧密,更便于误差传递,而各个单元之间的零件联系则相对松散,这一特征符合复杂网络的社团特性。如图5所示,网络中同属于一个社团的节点有着更为稠密的连接。社团检测是根据网络的拓扑结构解析出模块化的社团结构,从而以一种分而治之的方式研究整个网络的特性。根据识别出的社团之间是否重叠,即一个节点是否可以同时属于多个社团,可将其分为重叠社团检测和非重叠社团检测算法,其中重叠社团检测往往更加符合真实情况[21-22]。

图5 社团结构网络示意图
本文引入连边社团检测算法(LC)[23],其采用线图转换的思想,可以识别出网络结构中存在的重叠节点。此外,通过连边树图可以发掘网络的层次化结构,更加符合复杂机械产品的实际结构特点,便于在不同层次进行误差传递分析。传统的LC算法仅适用于无权网络,本文采用一种改进的LC算法用于复杂产品的装配单元划分,具体步骤如下。


图6 连边对的相似度定义
(10)
式中:wij为GW中节点i和节点j的连边eij的权重;n(i)={j|wij>0}是节点i的所有邻居节点的集合;ki=|n(i)|表示节点i的所有邻居节点的个数,当i=j时,δij=1,否则δij=0。采用Tanimoto系数[24]计算连边对eik和ejk之间的相似度
(11)
(2)根据步骤1所得相似度的值,并按降序排列这些连边对。
(3)按照步骤2所得排列次序,依次将连边对及其所属社团进行合并,并将合并过程以树图的形式记录下来,相似度相同的连边对在同一步进行合并。
(4)确定社团合并的停止点,确定最符合实际的树图分割位置,得到最终的单元划分结果。引入划分密度对社团的划分起参考作用,即划分密度最大时对应的社团划分可认为是最优的。假设一个包含X条连边的网络被划分为f个社团{P1,P2,…,Pf},其中社团Pf包含xf条连边和yf个节点,则整个网络的划分密度D为式计算
(12)
需要说明的是,不仅在最大划分密度所对应的最优分割处,树图的其他分割线也能得到有意义的社团结构,揭示出网络的层次化社团结构特征[25]。
3 实例分析
为了验证所提出的面向误差传递的复杂机械产品装配建模及单元划分方法的有效性,选取国内某型号汽轮机为研究对象。汽轮机产品精度要求较高,然而结构复杂(零部件多达几万至几十万),很难直接从整机出发进行误差传递分析。图7所示为该型号汽轮机低压模块B纵剖面图,下文将结合该模块进行分析。

图7 某型号汽轮机低压模块B纵剖面图
3.1 零件层级加权网络构建
根据装配工艺信息,获取该模块主要零部件,创建网络中的节点,并按照拼音大写首字母进行命名,例如,ZZ表示转子,GB-D6-U表示电机侧六级隔板上半,为方便后续表达,按照ASCII码从小到大的顺序给每个节点赋予一个节点号,如表2所示。

表2 零部件命名及编号(部分)
获取零部件间的装配关系及需要考虑的测量关系。参考企业人员意见,结合2.2节提出的加权方法,构建零件层级关联加权网络,该网络共有195个节点,346条边(其中装配关系286个,测量关系60个)。表3所示为部分零部件间关联关系及其属性。

表3 零部件间关联关系及属性(部分)
3.2 零件网络装配单元划分
根据2.3节所提出的装配单元划分方法,得到零件关联加权网络的合并过程及对应的划分密度如图8所示。观察网络的合并过程可以发现,该网络从含有346个单元(所有连边对分别属于1个单元)到最终只有1个单元(所有连边对都属于1个单元),从而揭示出层次化特征。其中,当相似度S为0.347时,划分密度最大(Dmax=0.121),此时含有196个单元,红色虚线表示划分密度最大时网络合并对应的分割处,此时仅有部分关联性特别强的零部件完成合并,例如一些键连接、销连接等。
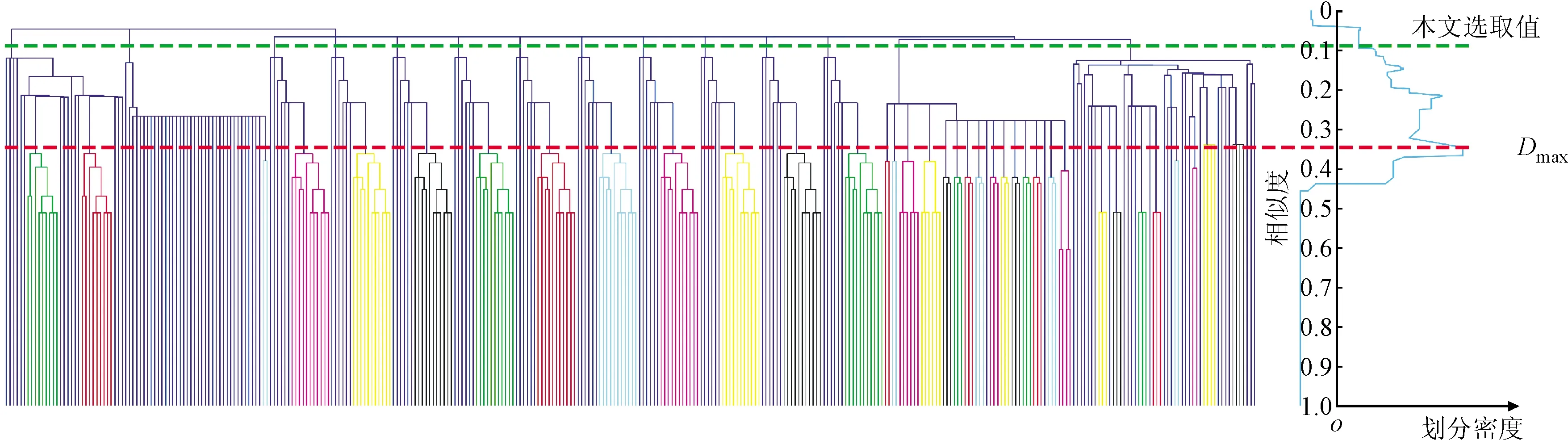
图8 合并过程的树图及对应的划分密度
本文所建立的某型号汽轮机低压模块B零件层级关联加权网络,划分密度最大时单元数量依然很多,有必要结合实际情况重新选择合适的分割点。表4所示为采用不同相似度分割阈值所对应的单元划分数量。在企业人员的建议下,以是否能够形成通流间隙、便于面向通流间隙的误差传递与分析为依据,本文以S=0.09作为网络合并的停止点,此时共有14个装配单元,图8中绿色虚线为本文采用的网络合并分割点。

表4 不同相似度及其对应的单元数量
具体的划分结果图9所示,图中不同颜色的节点分别属于不同的装配单元,因为本方法基于线图转换的思想,从而有效地识别出网络中的重叠节点(图中多种颜色表示的节点)。
根据划分结果,所得到的14个装配单元大致可归纳为:①2~6级电机侧和汽机侧隔板装配单元(共10个);②1级隔板装配单元;③汽缸装配单元;④轴承座及端汽封装配单元;⑤重要通流间隙单元。其中,①中的零部件均为隔板及其重要连接件;对于1级电机侧和汽机侧隔板,因通过导流环相互连接,形成汽流进入的第1个汽室,故②中将其共同作为一个装配单元与实际情况相符;③中汽缸及相关连接件作为隔板、导流环以及其他静子等重要零部件的载体,被成功划分到一个单元;④主要为两端的轴承及轴承座,以及端汽封等汽轮机两侧重要的零部件;⑤是转子与静子所形成的通流间隙单元,涵盖了网络中的多数测量关系。
划分结果表明,垫片(4、5号节点)、定位键(44号节点)、动叶(69号节点)、隔板汽封(132号节点)等为重叠节点。其中,定位键和垫片为隔板子单元与汽缸子单元的重叠零件,架起隔板和缸体误差传递的桥梁,同时也是实际装配中起调整作用的关键零件。动叶和隔板汽封是隔板子单元与通流间隙子单元的重叠零件,动叶与转子装在一起,然后装入汽缸缸体,动叶的围带和隔板的径向汽封形成叶顶通流间隙。隔板汽封在实际装配中首先与隔板装在一起,然后与转子形成通流间隙,是隔板与转子之间保证间隙的重要零件。
3.3 方法评价
根据装配单元划分结果可见,与现有方法相比,本文方法的优势主要体现在如下。
(1)成功揭示出复杂机械产品的层次结构,克服了传统单元划分方法仅有一种划分结果、常常难以符合实际情况的局限性。本文方法得到的层次划分结果为后续在不同层次进行误差传递与分析提供了基础,在实际应用中,可选择最合适的划分结果。
(2)有效识别出各装配单元之间存在的重叠零件。这些重叠零件是单元与单元之间误差传递的重要桥梁,在装配体中有着重要意义,是后续误差传递与分析中需要重点关注的关键零件。
4 结 论
(1)引入复杂网络理论,根据实际装配工艺信息获取零件列表、零件间装配关系以及必要的测量关系,构建了零件层级关联网络。
(2)采用模糊层次分析法与专家打分法相结合的方式,对零件间关联关系进行赋权,与传统专家打分法相比,在一定程度上提高了结果的客观性。
(3)基于零件网络的社团特性,采用改进的连边社团检测算法进行装配单元划分,不仅揭示出零件网络的层次性,便于在不同层次进行误差传递分析,还成功地发掘出属于不同单元的重叠零件节点,更加符合复杂机械产品实际结构特点。
(4)以某型号汽轮机低压模块B这一典型复杂机械产品为研究对象,验证了所提方法的可行性和有效性,从而为复杂机械产品装配建模与单元划分提供了新的思路。
(5)以本文方法所得到的装配单元为基础,可以进一步构建装配特征层级误差传递网络,从而为复杂机械产品装配质量分析提供了一个较为完备的分析平台。
