双向摩擦特性Dahl模型的布料仿真稳定性提升
2021-04-12刘志蕾吕梦雅
唐 勇,李 玲,刘志蕾,赵 静,吕梦雅
(1.燕山大学 信息科学与工程学院,河北 秦皇岛 066004;2.河北省计算机虚拟技术与系统集成重点实验室,河北 秦皇岛 066004)
0 引言
布料的仿真是计算机图形学研究的重要内容,但是由于布料类柔性织物的易变形性和灵活性,碰撞处理成为了布料仿真的主要瓶颈之一。碰撞一定会伴随摩擦的产生,所以正确考虑摩擦接触,对布料的仿真有着重要的作用。
2002年斯坦福大学的Bridson等[1]提出了一种方法,使用库伦摩擦模型来计算摩擦力的大小,根据弹簧排斥力的大小计算弹性力,然后用弹性力来评估库伦摩擦并且将排斥力与“撞击区”故障保护相结合,通过连续碰撞检测来检测碰撞的刚化区,这是最经典的处理摩擦接触的方法,同时也是本文理论研究的基础。2008年康奈尔大学的Kaldor等[2]针对针织布结构中的阻尼和摩擦滞后效应的问题提出了三组阻尼模型的方法,分别是质量比例阻尼、接触阻尼、非刚性运动阻尼,但是由于未采用适当的摩擦模型,所以导致计算结果不精确。2010年爱荷华大学的Williams等[3]提出了一种织物本构模型,能够捕捉各向异性、非线性和滞后的主要特征,并且可以在非线性、薄壳体、大形变、有限元框架中实现一般的穿孔交互式建模,但是这种建模缺失了内部摩擦,计算结果产生偏差导致系统稳定性较弱。2011年法国国立计算机及自动化研究院的Daviet等[4]引入了一种有效的求解器将精确的库仑摩擦考虑在内,然而,布料的模拟计算效率较低且实时性弱。2013年奥地利科技学院的Miguel等[5]提出了一种实时更新参数的内摩擦模型Dahl模型,并且证明这个模型能够有效地解决布料滞后的现象。但是该模型对于具有非常低的弯曲刚度和密度比的织物来说,弯曲摩擦估计结果不精确,导致实验实时性差。2013年北京航空航天大学的王华民等[6]开发了一个摩擦测量装置,通过从现实世界捕获的摩擦数据来推导出真实反映织物的复杂摩擦特性的摩擦模型,但是这种模型不能很好地捕捉静态摩擦,所以对布料仿真摩擦接触分析不精确。2017年宾夕法尼亚大学的Jiang等[7]使用物质点法改进拉格朗日方法,将布料建模为非牛顿流体并通过非光滑本构法自动考虑摩擦接触,但布料模拟的计算效率较低。2018年浙江大学的唐敏等[8]提出了一种基于GPU的交互布料模拟的增量碰撞处理算法,利用基于优化的求解器的连续迭代的空间和时间的相干性来进行碰撞响应计算,但是他们直接采用Bridson的摩擦模型,并没有考虑对摩擦模型进行改进。2018年加州大学的Guo等[9]采用了离散壳模型,利用Jiang等[7]的方法处理接触和碰撞,利用背景体积网格有效地处理复杂碰撞材料之间的接触力,虽然能够解释布料接触与精确的库伦摩擦,但是在碰撞处理过程计算效率低。2018年明尼苏达大学的Li等[10]提出了一种新的方法,使用物质点方法和细分有限元法的组合模拟摩擦接触的薄壳,但是很难保证实验的实时性。2019年胡安卡洛斯国王大学的Mickeal等[11]通过直接解决混合线性互补问题并省略了线性互补问题矩阵的构造来解决碰撞接触问题,他们建议使用共轭残差求解器作为碰撞响应系统的主干可以精确地处理摩擦,但是实际情况中摩擦处理替换为共轭残差求解器很难实现,由于不能精确地处理摩擦导致布料模拟稳定性弱。
综上可知,布料的仿真在碰撞和摩擦接触方面取得了很大的进步,但是在布料模拟过程中,计算效率低、布料运动稳定性差都成为了目前所要解决的问题。基于此,本文提出了Dahl模型双向摩擦特性的布料碰撞摩擦接触处理方法。与之前的方法相比,改进后的Dahl摩擦模型能够进行准确的碰撞检测和摩擦接触,保证计算效率的同时增强了布料运动的稳定性。
1 抗过渡变形的正三角布料建模
1.1 基于正三角网格质点弹簧的布料建模
为了更好地实现布料的真实感与实时性模拟,本文采用正三角形划分织物,在Choi等[12]提出的质点弹簧模型的基础上忽略未产生影响的剪切弹簧力,利用三角形的稳定性保持织物稳定,并采用对布料进行建模。采用该质点弹簧模型对布料进行建模,简单高效,且满足实时性需求。基于三角形网格的质点弹簧模型的结构如图1所示。
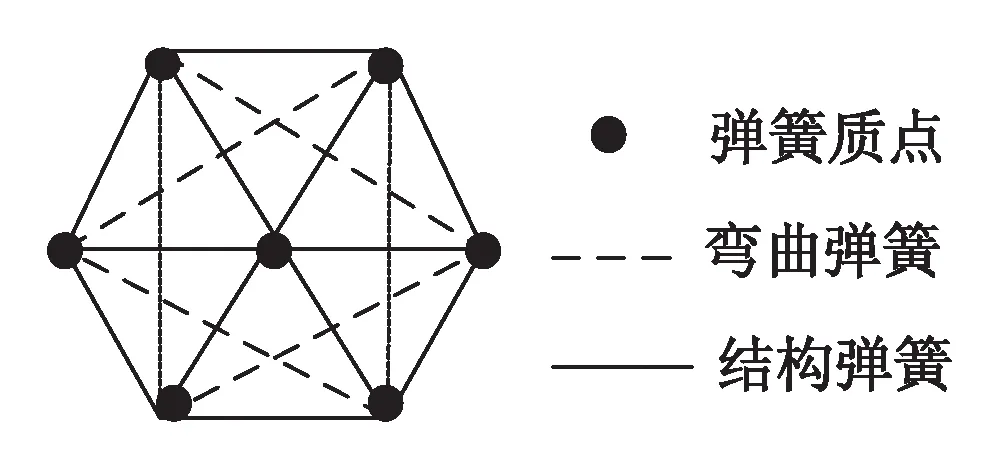
图1 三角网格质点弹簧结构Fig.1 Triangular mesh mass spring structure
本文在布料质点受力的分析中采用牛顿第二运动定律,对布料质点的质量、加速度以及受到的力进行了描述,即
(1)
式中,x表示质点的位置矢量,是实验的求解目标;m表示质点的质量;Finter(x,t)表示质点所受内力;Fexter(x,t)表示质点所受外力。本文中质点所受的力是随时间和位置所变化的。
1.2 “超弹性”问题中最大值的确定
如何有效解决超弹现象也是布料仿真中所面临的问题。在实际情况中,布料的受力与变形之间不仅是简单的线性关系,当布料的弹性形变超出一定的范围,就会产生复杂的非线性现象。
为了改善超弹现象,更加真实地模拟布料的受力情况,本文引入形变系数
B=|xij-d|/d,
(2)
通过设置形变系数的最大值Bmax来检测布料弹性的形变系数B。若形变系数超过了最大值,说明弹簧被过度的拉伸或者压缩,则重新调整弹簧d的长度,使得B=Bmax成立。其中d为不同弹性布料对应的自然长度,xij为弹簧从质点i到质点j的长度。
2 双向摩擦特性的Dahl摩擦模型
Dahl模型是一个连续模型,它是由一个非线性方程和一个力的输出方程所构成的:
(3)
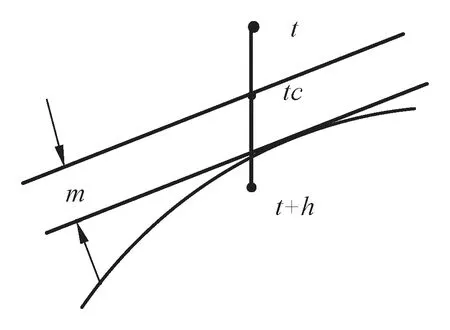
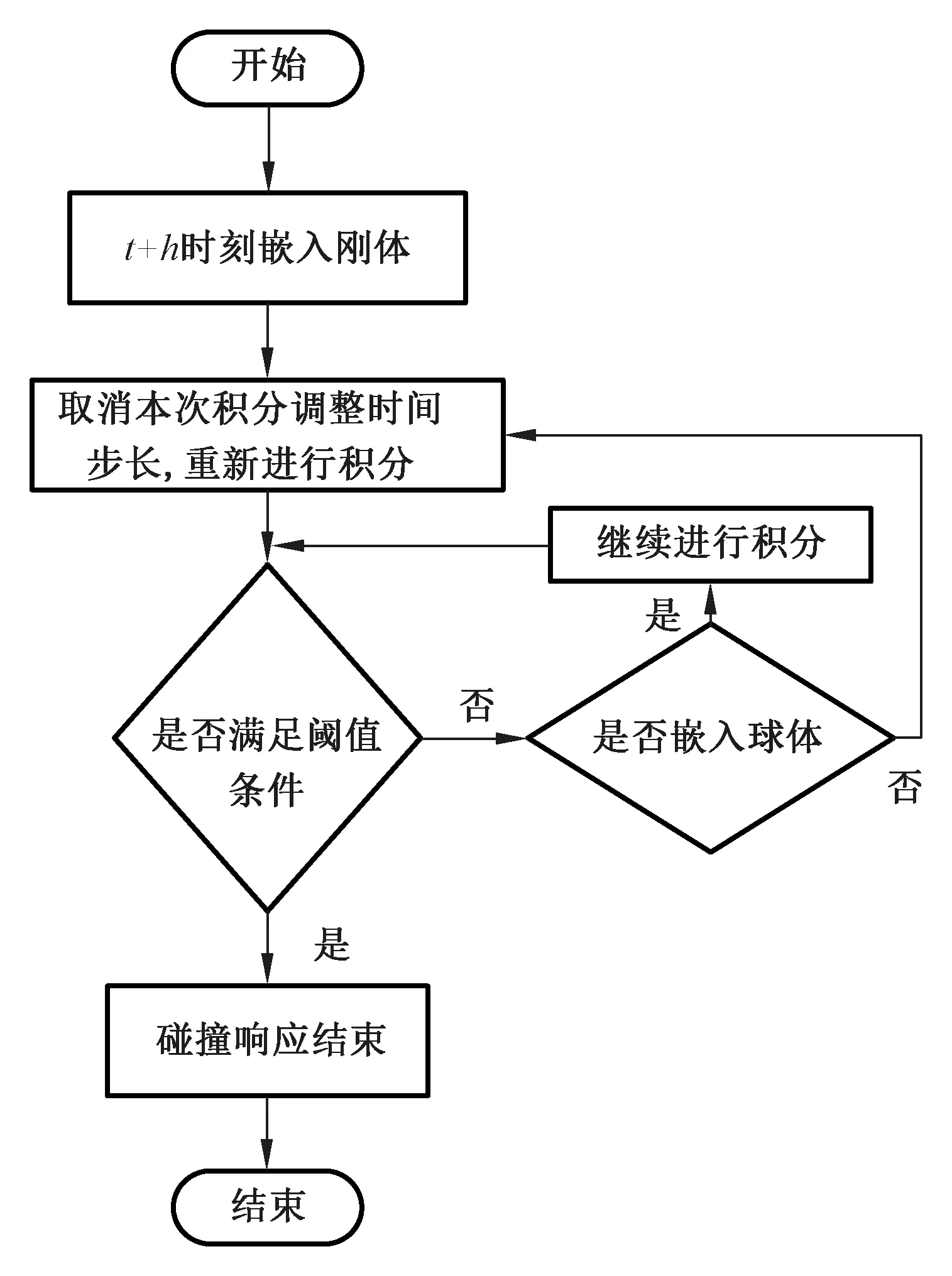
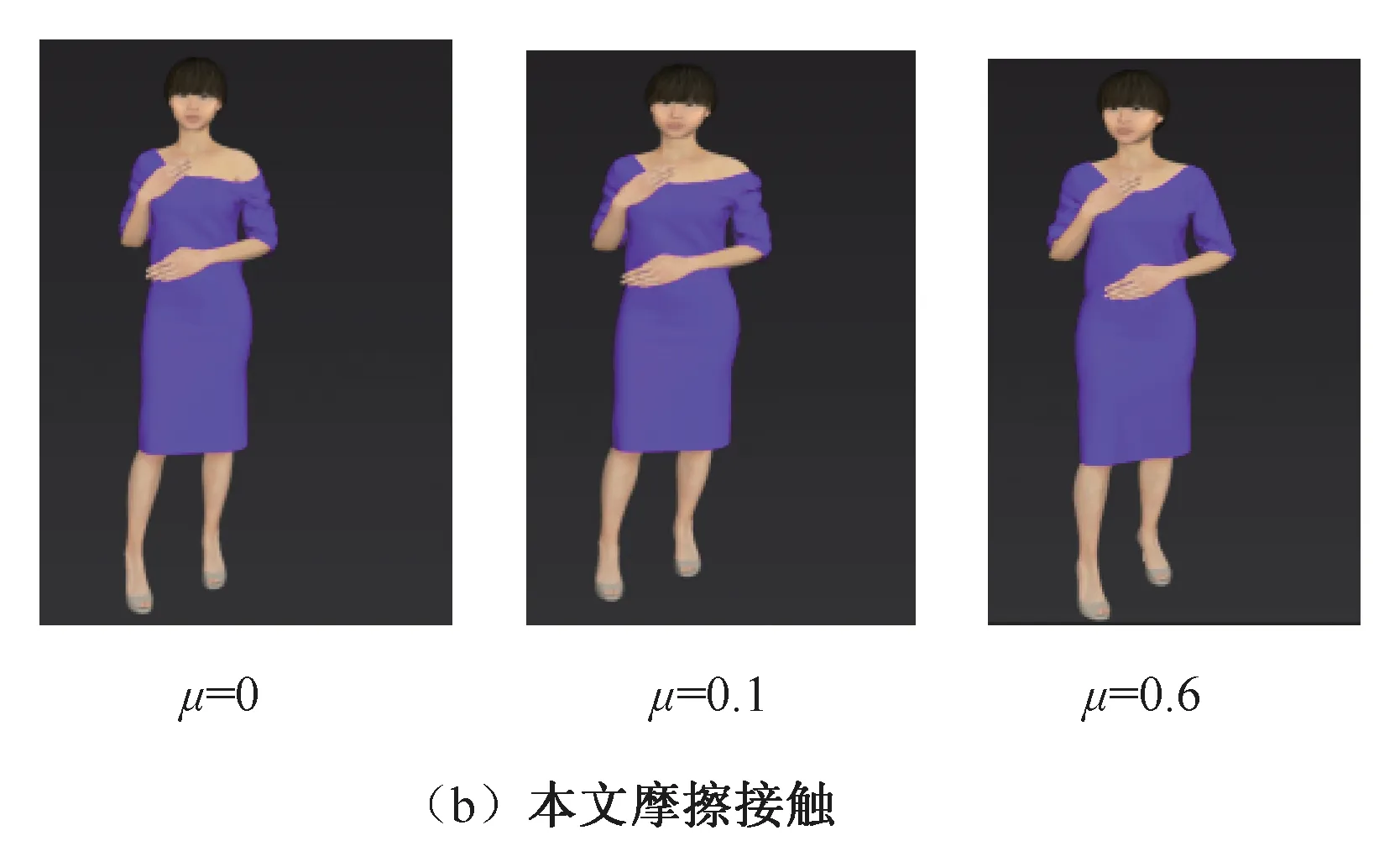
其中,z是摩擦模型的内部状态;v是相对速度;σ0是刚度系数;而F和Fc就是摩擦力和库仑摩擦力。根据式(3)可知,稳态时F=Fcsgn(v),即摩擦力等于库仑摩擦力Fc。停滞时,|F| 本文通过改变摩擦特性,控制速度和速度变量之间的关系,对Dahl模型做出如下改进: (4) 其中h(|v|)为符号函数,取值如下: 式中,v为相对速度;sgn(v)表示符号函数;Fs为静摩擦力;σ0为刚度系数;σ1为微分系数;Fc为库仑摩擦力;z0为外力作用下的位移;Δv为静摩擦力对应的速度段,Δv=0.001 m/s。 改进后的Dahl模型更好地模拟布料的摩擦接触现象而且同时增强了布料运动的稳定性。 在布料模拟的过程中,为了增加真实感,常常给布料附加各种外力,使其与周围的物体发生碰撞。碰撞检测算法总体划分为静态干涉检测算法和动态碰撞检测算法,但考虑到仿真的实时性,大多采用动态碰撞检测算法,其中比较经典的算法有层次包围盒法和空间分割法。考虑到本文选用的球体和桌子作为碰撞对象,所以采用简单易行的检测方法。若碰撞对象为球体,则要判断任意质点到球心的距离是否小于球体的半径。若碰撞刚体为桌子时,则要检测是否有质点落在桌子所处空间的区域内。 图2为传统的二分法处理碰撞问题的示意图,其核心是不断地调整时间步长。但是在仿真中为了得到精确的近似解往往需要大量的迭代,造成实验的实时性差。所以本文提出一种改进的二分法。 图2 二分法处理碰撞问题示意图Fig.2 Schematic diagram of the binary method fordealing with collision problems 图3 改进二分法流程图Fig.3 Improved dichotomy flow chart 1) 首先确定一个阈值m,作为碰撞检测时所允许的误差值,当质点与刚体表面的距离小于m时认为发生碰撞,否则认为没有发生碰撞。 4) 使用同样的方法重复以上步骤直到质点与刚体的距离小于假定的阈值为止。 图3为改进二分法的流程图。其中,k表示当前检测质点;al表示距当前质点位置距离最小值;ah表示距当前质点位置距离最大值;bl表示第一次优化后距当前质点位置距离最小值;bh表示第一次优化距当前质点位置距离最大值。 基于质点-弹簧的布料建模,本文采用改进的排斥力模型处理布料之间的碰撞。如果检测到质点与刚体发生碰撞时,则需要沿着碰撞面的法线方向添加一个与速度方向相反的排斥力。若与其碰撞的刚体是桌子时,排斥力的大小为常数,若为球体时排斥力为质点与球心距离的函数: Fp=g(Qs-Qc), (6) 其中,Fp为排斥力,Qs为发生碰撞质点的位置,Qc为碰撞球体球心的位置,g是映射函数。本文考虑到布料自碰撞时的摩擦现象,本文将在碰撞质点速度相反的方向施加摩擦力,减少碰撞次数,提高布料运动的稳定性。 本文实验基于Windows 8 64位操作系统,使用Unity3D开发平台建立了布料仿真模型。硬件环境为:Intel Core i7 4790 3.60GHz,16 G RAM,显卡为NVIDIA GeForce GTX 750 Ti。 如图4所示,图4(a)为未引入形变系数的效果图,被固定的两端明显的过度拉伸,图4(b)为本文引入形变系数的效果图,符合实际布料的悬挂效果,由实验结果可得,通过引入形变系数有效地解决了超弹现象增强了布料模拟的真实性。 图4 超弹现象的实验对比图Fig.4 Experimental comparison chart of hyperelastic phenomenon 如图5所示,图5(a)为不同风场相同材质(丝绸)布料与桌子之间的摩擦;图5(b)为相同风场不同材质(丝绸、锦缎、棉麻)的布料与桌子摩擦的效果(μ为不同材质布料的摩擦系数,摩擦系数影响公式(5)中库伦摩擦力Fc的大小)。从图中可以看出,在风场强度q的作用下,本文的方法不仅能够正确模拟布料与刚体之间的摩擦而且避免了布料自碰撞所产生的穿透现象。 图5 不同材质和风场布料与圆桌交互效果图Fig.5 Different materials and wind field cloth and round table interaction diagram 图6分别展示了文献[10]和本文的方法模拟的刚体与连衣裙摩擦交互效果,文献采用的是库伦摩擦模型,而本文采用的是双向摩擦特性的Dahl摩擦模型来进行摩擦接触处理,从视觉上可以看出,本文的方法更能够准确地模拟变化的摩擦系数μ的效果。 图6 人体模型与布料摩擦接触效果图Fig.6 Rubbing contact effect diagram between human body model and cloth 图7为本文与文献[14]的对比图,在模拟布料与小球的碰撞实验中,文献所使用是改进的基元相交检测算法与能量耗散的方法来处理布料与物体的碰撞问题,本文通过插值法的思想改进积分时间步长的二分法进行了碰撞响应处理,很明显本文实验效果更加逼真细腻。表1描述了两个对比实验场景中布料的属性参数。在与文献[12]对比时,文献中只给出了顶点与接触点的平均数目没有给出面片数,所以采用相同布料分辨率作为依据,由于本文在实验过程中整合了大量的计算,简化了计算过程,所以迭代次数存在较大差距。在布料与小球碰撞实验中,通过不同的方法模拟相同实验对比得到,本文方法在实时性上更具有优势。 图7 本实验场景与文献[14]的对比图Fig.7 Comparison between the experimental scene and the literature [14] 表1 不同方法的实验性能对比表 Tab.1 Comparison of experimental performance of different methods 本文提出了一种基于双向摩擦特性的Dahl模型对布料摩擦接触进行模拟仿真的方法,通过采用改进的Dahl模型和二分法使得本文不仅有效地处理了布料与刚体之间的碰撞问题,还降低了计算量,提高了仿真的速度,在人体与布料摩擦的试验中帧率增长了47%,在布料与小球碰撞的实验中帧率增长了10%。同时通过因为形变系数改善了布料的超弹现象,在超弹现象的实验中明显可以看出,改进后的布料仿真更具有真实感。 目前只考虑了各向同性的布料交互的情形,今后会继续将本文的方法拓展到各向异性的布料,并实现各向异性布料的摩擦接触。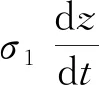
3 碰撞响应
3.1 时间步长优化二分法的碰撞响应
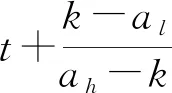
3.2 碰撞响应中的力学模型
4 实验结果与分析





5 结论
