含异物击打伤高速动车组车轴疲劳寿命预测

2021-04-10

中国铁道科学 2021年2期

（中国铁道科学研究院集团有限公司金属及化学研究所，北京 100081）

车轴是高速动车组的关键部件。车轴断裂极有可能造成动车组脱轨，导致灾难性的后果。根据欧洲铁路管理局（ERA）铁路安全性能报告的统计，平均约每5 000 万km 运营里程发生1次断轴事故。断轴事故调查分析表明，高周疲劳是车轴的主要失效模式[1]，且以车轴表面缺陷导致的疲劳最为常见。动车组高速运行时异物很有可能高速冲击车轴，形成外物损伤缺陷（Foreign Object Damage，FOD）。FOD周围的残余应力场对短疲劳裂纹扩展有显著影响[2-4]。部分学者分析了高铁车轴表面典型缺陷的表征方法和疲劳特性，研究缺陷大小等参数对车轴疲劳性能和疲劳寿命的影响规律[5-6]。部分学者从断裂力学或损伤的角度评估了车轴的疲劳强度和损伤容限[7-11]，表明小于临界尺寸的表面缺陷对25CrMo4 车轴或EA4T 车轴的疲劳强度几乎没有影响。但也有研究表明，超过临界尺寸的表面缺陷将导致车轴在低于疲劳极限的载荷作用下断裂[12-13]。疲劳损伤是与时间正相关的塑性应变高度局部化损伤，基于此理念提出损伤过程区（Damage Process Zone，DPZ）的概念[14]，认为疲劳损伤局限在DPZ 中。可引入疲劳指示参数（Fatigue Indicator Paramter，FIP）[15]表征累积损伤的程度，进而建立FIP与疲劳寿命的关系。

在修程修制改革的工作要求下，延长检修周期成为车轴运维的必然要求。而车轴表面击打伤影响车轴疲劳性能，成为延长检修周期的制约因素。为预防由于FOD 引发的断轴事故，维护铁路运输安全，有必要加强对车轴FOD 问题的深入研究，为动车组车轴修程修制改革提供试验基础和理论支撑。

本文以小试样寿命预测模型为基础，考虑尺寸效应，构建含异物击打伤实物车轴寿命预测模型。以缺陷尺寸和交变应力为主要参量，对实物车轴进行寿命预测和台架验证。

1 试验设备、材料和方法

1.1 小试样疲劳试验

试验用疲劳小试样取自动车组新造EA4T车轴轴身距表面10 mm处，光滑小试样尺寸如图1所示。采用升降法确定疲劳极限，按成组试验法在较高应力水平下进行试验。试验设备为四连式悬臂梁型旋转弯曲疲劳试验机。

图1 旋转弯曲疲劳小试样（单位：mm）

采用霍普金森压杆（SHPB）试验方法模拟车轴表面异物击打伤，试验装置如图2所示。试验时，采用正方体状钨钢弹丸高速冲击旋转弯曲疲劳小试样长度方向的中部位置，冲击速度为100 m·s-1。钨钢弹丸与车轴钢试样的接触方式较为随机，有面接触、棱边接触以及角接触3种方式，如图3所示。考虑较不利情况，选取棱接触或角接触损伤试样进行旋转弯曲疲劳性能测试。

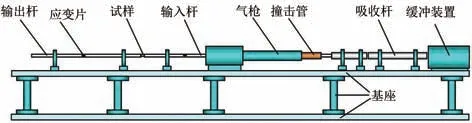
图2 霍普金森压杆（SHPB）试验装置

图3 模拟冲击损伤时钨钢弹丸与车轴钢试样接触方式

1.2 实物车轴台架试验

试验用实务车轴为某CRH380BL型动车组A4级修时表面含严重异物击打伤车轴，如图4所示，已运行76.334 万km。将轮对退卸后的含击打伤车轴按要求加工疲劳试样，压装工装轮后组成半轮对，在全尺寸疲劳试验台上进行疲劳试验，如图5所示。该设备的原理是使测试试样的振动频率尽可能接近共振频率，通过一定的振幅在试样的测试截面上获得目标应力水平。

图4 含异物击打伤车轴

由于动车组车轴强度校核中，动力车轴空气制动最大截面应力118.8 MPa，动力车轴正常行驶过程中载荷均小于70 MPa。因此，台架试验时选用最苛刻的118.8 MPa 恒定载荷施加于考核缺陷处。采用Shapescan3D GFM 现场型光学三维划痕缺陷测量仪对缺陷位置、深度、面积、体积以及缺陷底部尖锐程度进行统计。

图5 轮轴全尺寸疲劳试验台

采用测量设备得到含异物击打伤车轴的典型形貌及其横截面尺寸如图6所示。测量结果表明，击打伤深度一般不超过2 mm。

图6 含异物击打伤车轴典型形貌和横截面尺寸

1.3 基于FIP的疲劳寿命预测

对于含异物击打伤车轴，引入缺陷临近区域的应力场强度（应力场强度与缺陷尺寸、远场应力、车轴的形状尺寸等相关）、滑移系上的循环变形等参数构建FIP，FIP的表达式[16]为

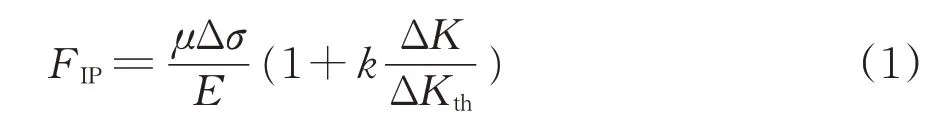
其中，

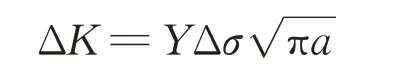
式中：FIP为FIP值；μ为施密德（Schmid）因子；Δσ为循环应力幅值；E为弹性模量；k为与材料缺陷敏感性相关的常数，取值在0.5～1.0 之间；ΔKth为代表损伤起始的应力强度因子幅值；ΔK为缺陷附近的最大应力强度因子；Y为形状因子；a为裂纹深度。

对含缺陷疲劳小试样的疲劳性能进行数据拟合，得到FIP与疲劳寿命之间的关系为

式中：Nf为疲劳寿命；α和β为拟合参数。

2 试验结果与讨论

2.1 含缺陷小试样的疲劳寿命预测

根据疲劳试验数据，得到小试样S-N曲线如图7所示。由图7可知，光滑小试样疲劳极限为352 MPa，含缺陷小试样疲劳极限为240 MPa。

图7 小试样S-N曲线

基于FIP 损伤参量的理念，对小试样疲劳寿命进行预测。对于EA4T车轴材料，Schmid因子μ取

0.49[17]，E取210 GPa，ΔKth取10 MPak取1。由式（1）可知，FIP 取决于外加循环应力Δσ、缺陷深度a和与试样尺寸相关的形状因子Y。

FIP值与疲劳寿命Nf的关系如图8（a）所示，拟合得到含缺陷EA4T车轴材料疲劳小试样寿命预测模型如式（3）所示，疲劳寿命预测结果评价如图8（b）所示。

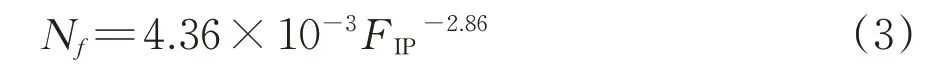
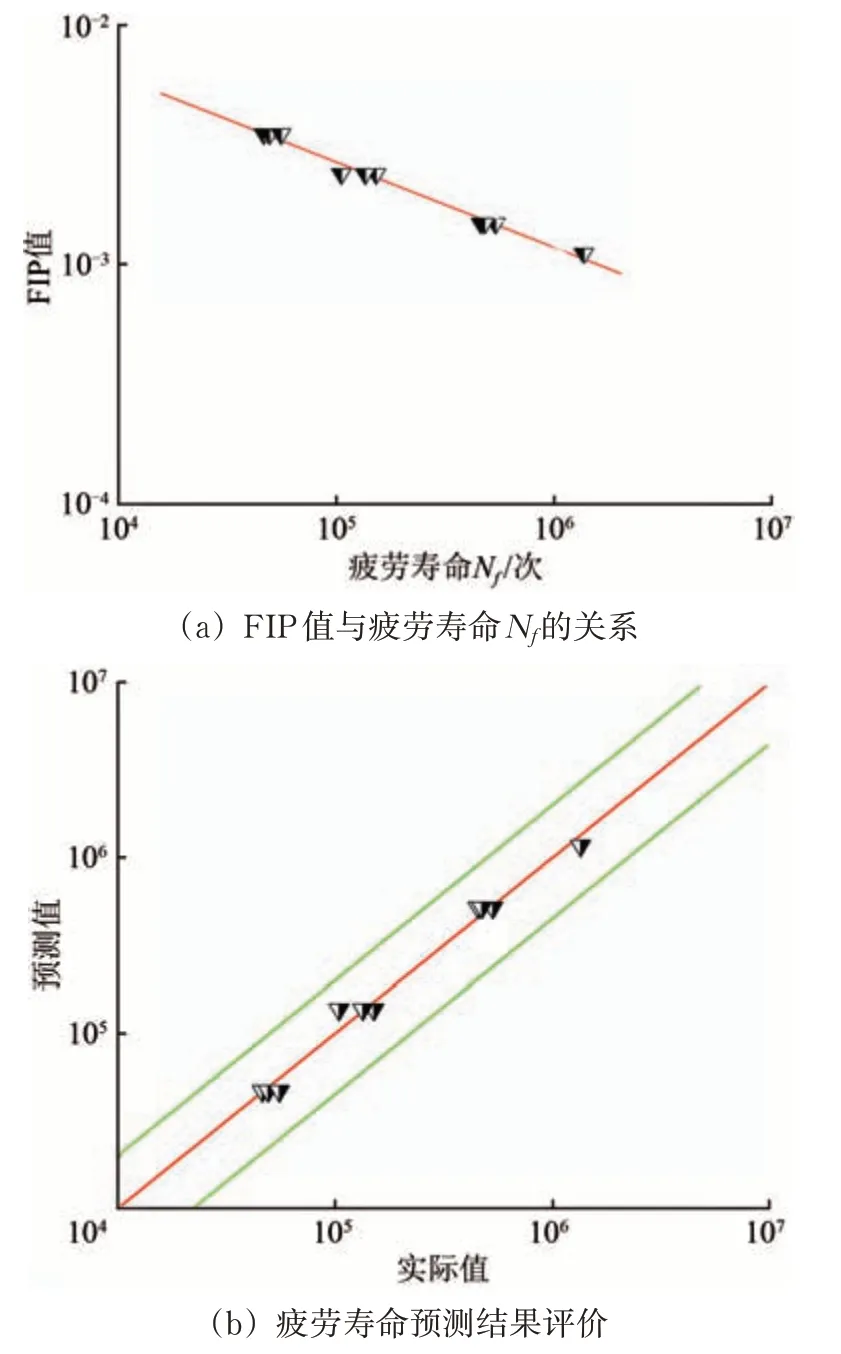
图8 含击打伤EA4T车轴材料疲劳小试样寿命预测

由图8（b）可知，疲劳寿命试验数据均在预测值的2倍线内，说明预测模型具有很高的精度，基于FIP的寿命预测模型适用于车轴疲劳寿命的预测。

2.2 缺陷处残余应力

依据车轴疲劳小试样和正方体钨钢弹丸尺寸，采用Abaqus 软件构建有限元模型。为保证冲击仿真的精度，在疲劳小试样中部与钨钢弹丸接触位置进行网格加密处理。为获取冲击后损伤附近区域的残余应力，在疲劳小试样的2端施加无反射边界条件，以缩短数值计算时疲劳小试样内部应力趋于稳定的时间。疲劳小试样和钨钢弹丸的有限元模型及网格划分如图9所示。

不同钨钢弹丸与疲劳小试样接触方式下冲击损伤附近区域的残余应力云图如图10和图11所示。

从图10可知：在各个接触方式下冲击损伤附近区域的残余应力分布特点基本相似，均为冲击损伤上下2侧存在局部的拉伸残余应力，而左右2侧存在一定程度的压缩残余应力。

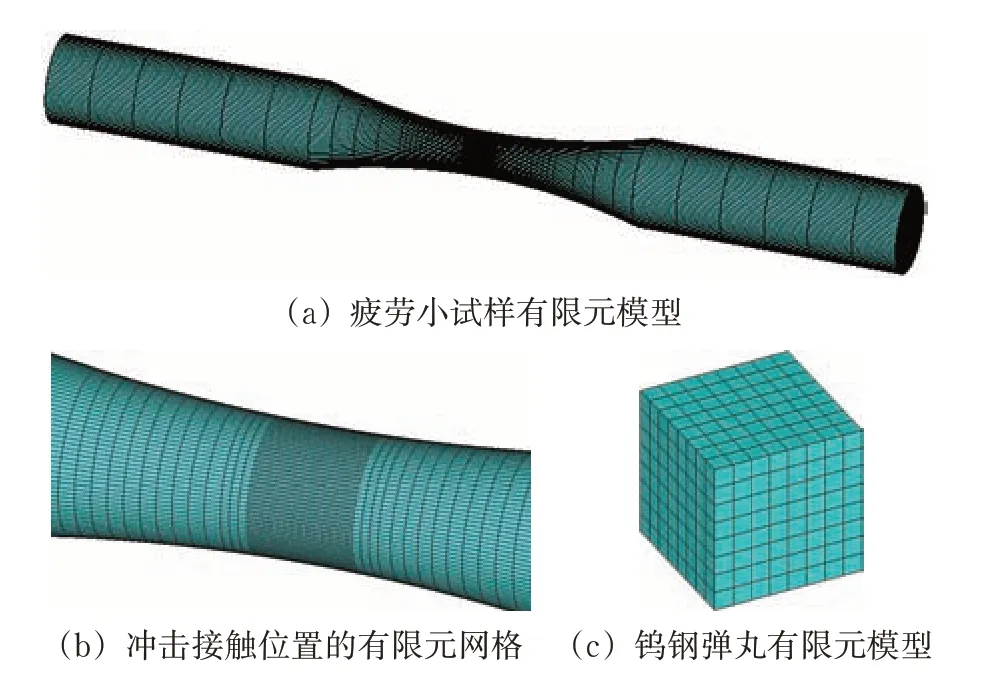
图9 疲劳小试样和钨钢弹有限元模型

从图11可知：在冲击损伤底部存在一定范围的压缩残余应力，并且在其所在区域的下方，还存在一定程度的拉伸残余应力，这种分布特点基本在各个接触方式中均有体现。

不同接触方式下疲劳小试样表面冲击损伤形貌如图12所示。从图12可知表面冲击损伤在小试样表面的具体分布和整体形态。

图10 不同接触方式下冲击损伤正视图（轴向）

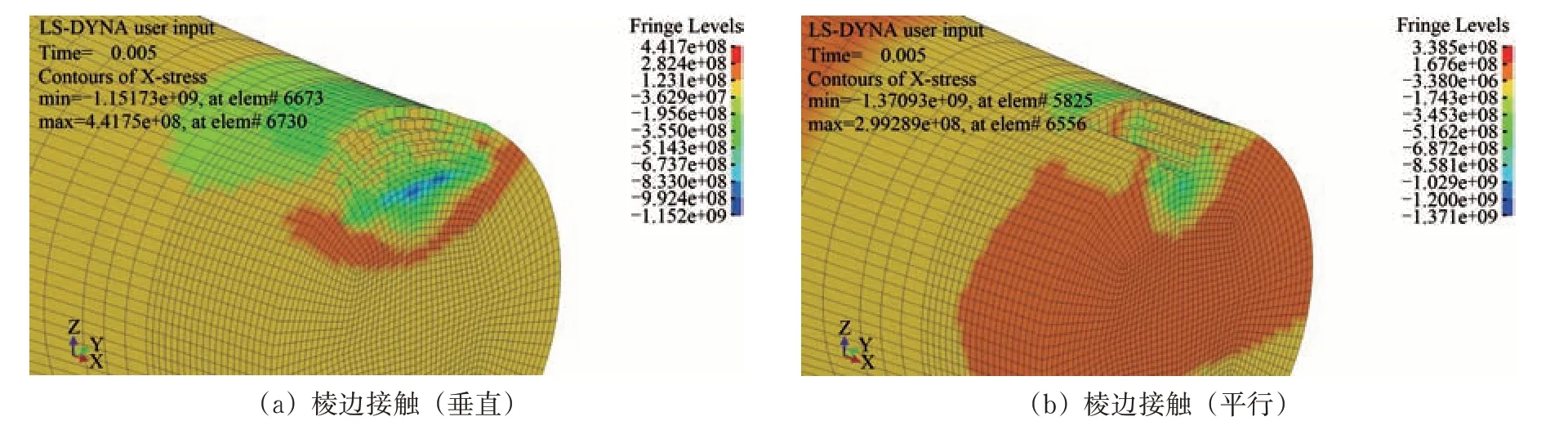
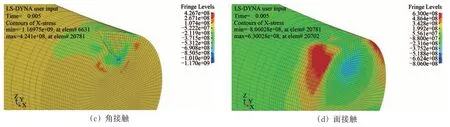
图11 不同接触方式下冲击损伤剖面图（轴向）

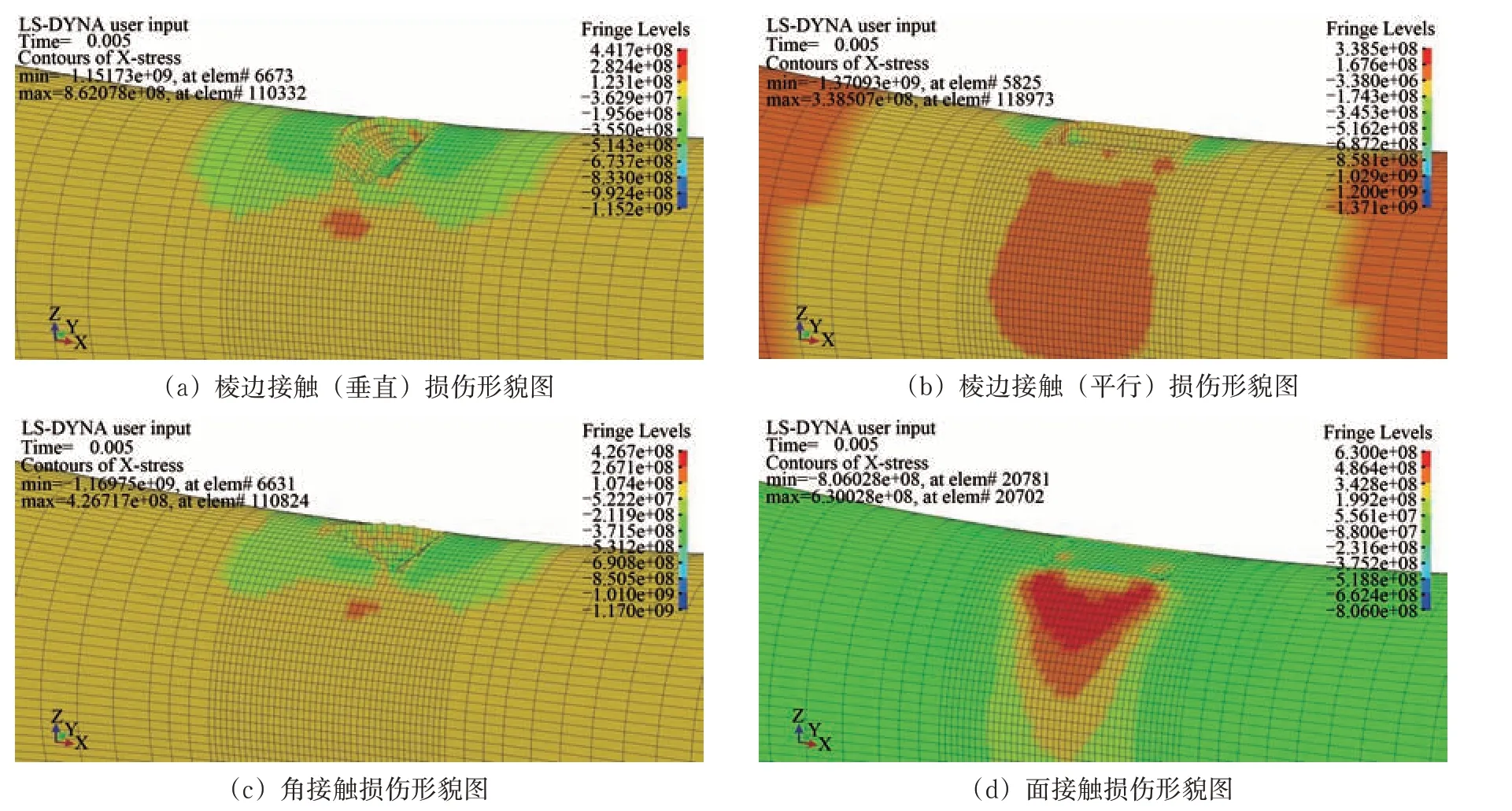
图12 不同接触方式下冲击损伤形貌图（轴向）

从残余应力的数值上对比看出，面接触冲击形成的拉伸残余应力水平最高，残余应力的数值分布较为明显；而角接触的冲击损伤虽然很大，却没有较为明显的残余应力分层。导致这种现象的主要原因是冲击过程中材料的损失导致一部分冲击能量释放。因此，对于面接触来说，大部分的冲击能量转化为材料的应变能，所以存在着较高水平的残余应力。

为验证仿真结果的可靠性，对仿真得到的冲击损伤尺寸与实际的冲击损伤尺寸范围进行对比，结果见表1。表中：在实测情况下面接触可视为棱边接触（平行）的特殊情况，因此二者统一比较。

表1 冲击损伤尺寸的仿真结果与实测对比 mm

从表1可知：数值模拟的冲击损伤尺寸与实际的大小基本相同，多组模拟损伤的尺寸数据均在实际测量的尺寸范围内；模拟的损伤深度较高于实测数据，推测其主要原因是J-C模型中断裂塑性应变的选择较为单一，使得仿真过程中模拟的单元失效无法完全反映实际材料的失效状况，从而导致模拟损伤与实际损伤的尺寸存在一定的差异。

2.3 含击打伤车轴疲劳寿命预测

采用基于FIP的方法，预测含击打伤车轴的疲劳寿命。在交变应力幅值和裂纹深度相同的情况下，实物车轴与材料级别的小试样相比，除应力强度因子表达式中的形状因子Y不同外，其他参量均相同。为构建小试样与实物车轴间缺陷形状因子的定量关系，在交变应力幅值和裂纹深度相同条件下，以缺陷小试样FIP寿命预测模型为基础，建立含击打车轴FIP寿命预测模型。

1）车轴尺寸的影响

车轴为典型的圆柱形结构，疲劳失效的主要载荷类型为旋转弯曲载荷，疲劳裂纹的形式为椭圆形表面裂纹。

车轴形状因子Y表示为

其中，

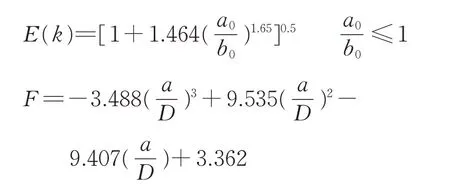
式中：a0为车轴表面椭圆裂纹短半轴；b0为车轴表面椭圆裂纹长半轴；D为动车组车轴轴身直径。

则车轴裂纹应力强度因子为

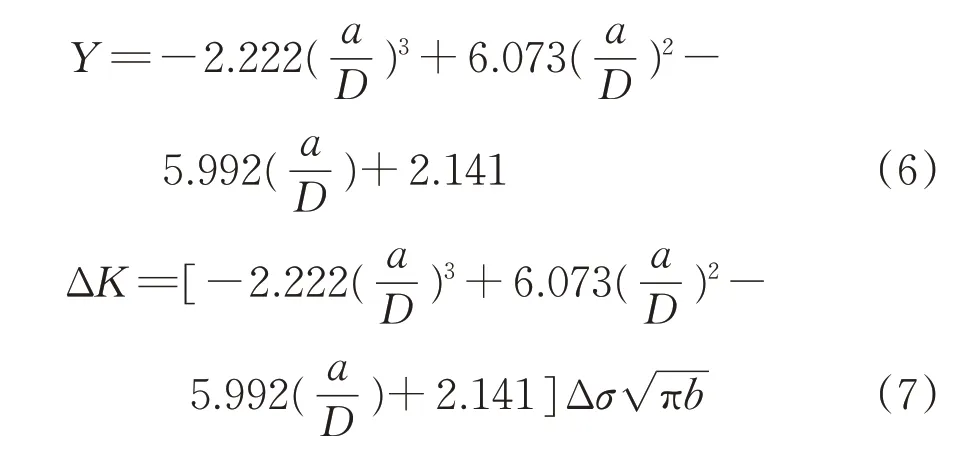
将式（7）代入式（1），可得考虑不同尺寸的FIP值为

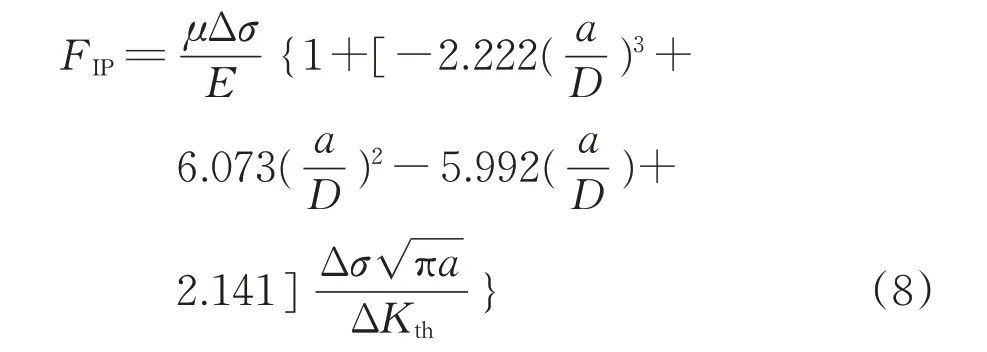
式（8）体现了车轴直径、缺陷尺寸、交变应力与FIP值的关系。

2）缺陷尖端曲率半径的影响

裂纹尖端的弹性应力与裂纹深度a和裂纹尖端的曲率半径ρ相关，当a≤ρ时，裂纹尖端的弹性应力ΔσTip为

在裂纹深度相同的情况下，车轴表面冲击损伤附近区域的弹性应力取决缺陷底部的曲率半径。测量含击打伤车轴冲击损伤底部的曲率半径如图13所示，试验得到损伤缺陷底部的曲率半径均值为0.50 mm。

图13 3个典型缺陷底部的形状

对于车轴材料为EA4T的疲劳裂纹，裂纹尖端的曲率半径小于0.05 mm，基于保守考虑，裂纹尖端的曲率半径取值0.05 mm。

在深度和远场应力相同的情况下，缺陷尖端的应力幅值Δσd与裂纹尖端的应力幅值Δσc的关系为

式中：ρc和ρd分别为裂纹和缺陷尖端曲率半径。

则对于含冲击打伤车轴，冲击损伤附近区域的FIP值为代入参数数值，车轴直径以273 mm计算，得

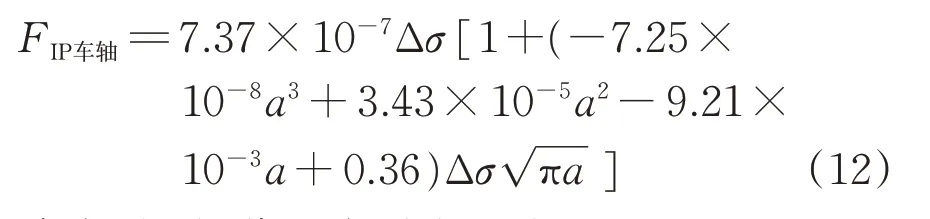
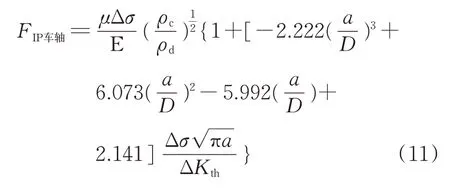
将式（12）代入式（3）可得

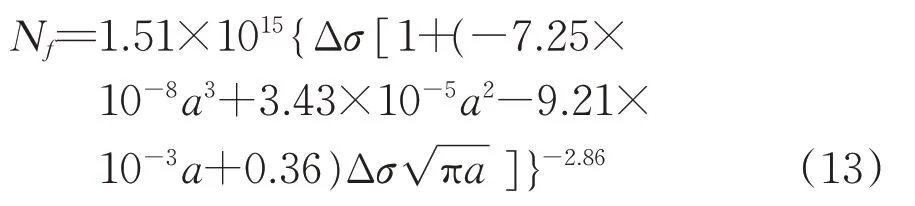
以深度作为缺陷的主要参量，分别取0.2，0.5，1.0，2.0，3.0 和5.0，应力分别取30.0，40.0，50.0，60.0，70.0，87.0，118.8 和145.0 MPa，根据式（13）分别计算车轴的疲劳寿命，预测结果见表2所示。以复兴号车轮直径920 mm为例，预测行驶里程见表3。以缺陷尺寸和交变应力为自变量，疲劳寿命和行驶里程为应变量的结果如图14和图15所示。

表2 含击打伤车轴在不同缺陷深度下疲劳寿命

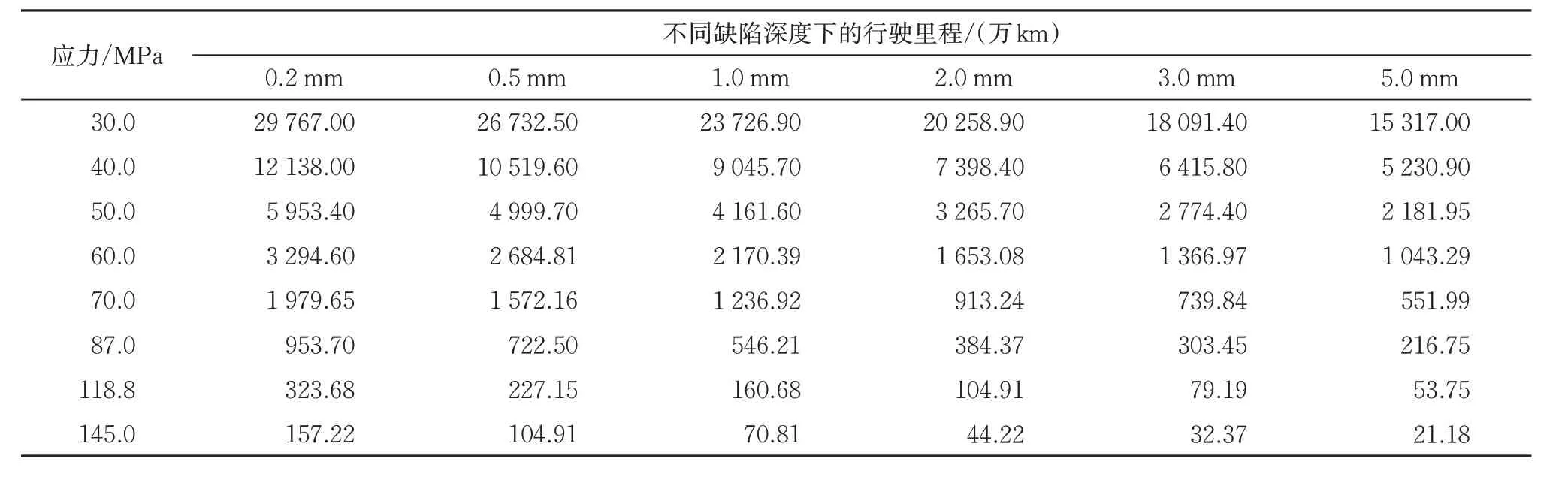
表3 含击打伤车轴在不同缺陷深度下行驶里程

图14 含击打伤车轴在不同应力水平下疲劳寿命

图15 含击打伤车轴在不同应力水平下行驶里程

2.4 台架试验验证

对台架试验用实物车轴表面击打伤进行表征，得到最严重缺陷参数如下：距离下端轮座距离190 mm，深度997 μm，缺陷面积18.45 mm2，缺陷体积4.93 mm3，缺陷底部夹角94.05°，在此缺陷其附近粘贴裂纹监测应变片作为台架试验考核位置。

将118.8 MPa恒定载荷施加于上述缺陷处，循环比R=-1，扩展一定循环周次（108次）后，对车轴进行磁粉探伤，未发现表面裂纹。该试验已属超高周疲劳范畴。

如果把该缺陷规整为深度1.0 mm 缺陷，在最苛刻受力条件下，通过寿命预测模型，循环周次可达5.56×108次，以复兴号为例可行驶160.68 万km，超过CRH1型、CRH3型和CR400AF/BF 动车组车轴三级检修周期（120±12）万km 或3 a的检修要求。因此，运用检修中对于深度小于1.0 mm的击打伤类缺陷可不做打磨或其他处理。