梯形直觉模糊双矩阵对策模型及求解方法的探讨

王焕庭

(桐城师范高等专科学校 商贸与电子信息系，安徽 桐城 231400)

0 引言

在对有关相互作用策略的大量研究中发现，矩阵对策理论的应用十分广泛.信息的不确定性往往使局中人难以对预计的支付值进行准确的判断，因而近似估计支付值的引用显得极具必要性.现有的研究成果中，Zadeh[1]所提出的采用模糊集替代收益矩阵或策略集的方法仅能给出“是”或“否”的答案，无法描述心理上的倾向性；Atanassov[2]提出的两标度模糊集对隶属度和非隶属度均进行判断，量化地描述肯定、否定、犹豫三种心态所达到的程度，从而以十分灵活的方式对不确定性进行有效的处理[3-5]，由此可见以直觉模糊集表征支付值的对策具有很强的实用性.

基于直觉模糊集制定所需策略的过程中需要对互不相容的隶属度与非隶属度的向量进行比较，可能会出现结果截然不同的现象，因此需要进一步研究直觉模糊博弈的解决方法[6-8].模糊矩阵对策的获取过程为：基于对策均衡解的定义创建模糊结构模型，接下来采取特殊的方式对模糊数进行处理，其重点是必须采取正确的排序方式，最后将模糊结构转换为标准数学结构，从而求解并获取模糊矩阵的对策.本文提出了一种对梯形直觉模糊双矩阵对策模型求解的方法，结合局中人的个性化需求对模糊量进行合理排序，以贴近现实应用的方式对模糊矩阵模型进行求解，并最终得到了合理的解决策略.

1 直觉模糊数的排序

1.1 定义与计算

两标度直觉模糊集能够明确描述肯定、犹豫、否定三个状态的程度，在不确定性处理中最为灵活实用.

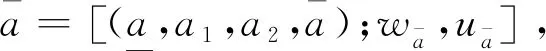
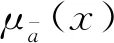
(2)

1.2 排序方法

(3)

(4)

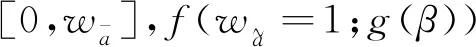
(5)

(6)

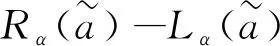
(7)

(8)

同理，式(5)、式(6)可转换为

(9)

(10)

(11)

(12)

(13)

由此，通过值指标与模糊度指标的差异实现了直觉模糊数的排序.对照业内公认的模糊数排序方法可行性标准，本文所提出的排序方法符合大部分排序特性公理，因此对于任意的两个梯形直觉模糊数，在0≤≤1的条件下，以下各式均成立：

2 基于风险倾向的梯形直觉模糊双矩阵模型及其求解方法

2.1 模型的创建

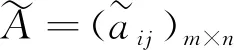
若当局人P1选择的是组合策略y(y∈Y)，当局人P2选择的是组合策略z(z∈Z)，那么在支付值为梯形直觉模糊数的情况下，二者的预计支付值分别为

其中(y,z)代表二者的组合策略相同.

2.2 模型的求解

(14)

其中，u(1)与v(2)为不同局中人的不同决策变量.

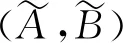
3 算法验证

生产和销售同类产品的两家公司M1和M2同时在某地市场进行产品推广，两者都希望通过制定合理的销售计划来抢占更多的市场份额.M1公司的销售计划中主要包含两种策略供决策者选择，策略a1为加大广告宣传力度，策略a2为提升产品包装辨识度.M2公司的销售计划同样以上述两种策略为主，分别记为β1和β2.由此，两家公司对于销售策略进行选择的过程可视为对双矩阵对策模型的求解，M1和M2公司分别对应模型的局中人P1与P2.考虑到市场环境的多变性以及各种市场信息的不确定性，两家公司很难确定未来一个时期内产品的真正销量，因此只能通过模型求解获取一个附加了不确定因素的近似结果.两家公司基于4种销售策略组合下的支付值梯形直觉模糊双矩阵表达式分别为:

通过式(14)对矩阵对策双现行规划模型进行求解，得到双矩阵参数模型如下：

max{(45.25+4.25λ1+9.17λ2)y1z1+(23.25+12.25λ1+4.08λ2)y1z2+(16.67+3.58λ1+7.17λ2)y2z1+(42.33+9.17λ1+5.08λ2)y2z2-u(λ1)-υ(λ2)},

(15)

根据两家公司管理层的实际风险倾向对λ1和λ2在[0，1]内进行取值，代入式(15)后即可求得预计支付值并获得最优策略，具体结果如表1所列.

通过表1中的数据可知，每个局中人的理想预计支付值和能够实现其目标的最优策略均取决于其自身的风险倾向.其中，理想预计支付值与其风险倾向呈正相关关系，风险倾向值越高，局中人的理想预计支付值越大.而局中人所能选择的最优策略与其风险倾向呈负相关关系，即风险倾向值越高，最优策略值就越小.因此，为实现某一目标选择具体的操作方案时，必须考虑局中人的风险倾向因素.

表1 两家公司基于不同风险倾向(部分)的预计支付值与最优策略

4 结束语

在可以通过多种方案实现某一目标的情况下，首先必须对各种方案的支付值进行预估和排序，以便从中选取最优质的方案并获得最好的结果.为此，本文提出了一种基于局中人风险倾向的梯形直觉模糊双矩阵对策模型求解方法，介绍了直觉模糊数的定义和排序方式，阐述了梯形直觉模糊双矩阵模型的创建过程及计入了风险倾向因素的求解方法，实际应用结果表明，所提出的方法切实有效，能够很好地解决现实中的直觉模糊数矩阵对策问题.