基于巷道堆垛式立体车库存取策略的研究

刘 麒，张 野，王 影，徐姣姣，李宝华，苟 垚

(吉林化工学院 信息与控制工程学院，吉林 吉林 132022)

近年来，随着人民生活水平提高，私家车保有量逐年增长，但土地资源有限，传统平面化停车泊位规模无法满足人们日常停车需求[1-2].立体车库因有占地面积小、空间利用率高、成本低等优点而迅速得到发展，立体车库的迅速发展在改善城乡停车难，有效缓解道路交通压力上发挥着重要的作用[3].由于城乡车辆流动性大，存取车辆时间长、效率低是当前市场面临的 “痛点”[4]，立体车库在运行过程中，车辆的存取策略直接影响车辆存取时间，如何有效地缩短存取时间，提高车辆的运行效率，减少顾客的存取时间成为当前研究学者的重要课题.

为了解决城乡停车问题，国内外学者针对停车难等问题做了大量的研究.在国外，Lerher等[5]通过对车库结构特点以及存取流程的分析，建立相关的数学模型，分析比较不同存取策略对时间长短的影响；Geng等[6]通过排队论为基础对存取车的概率性以及存取作业的时间进行了相应的优化，进一步提高了存取作业时间.在国内，张刚刚等运用排队理论对不同存取策略采用相同次数操作，对不同时间段存取策略仿真比较，选择合适存取策略[7]；何国旗等利用MATLAB对比分析不同策略下的效率，然而国内立体车库仍然存在一些需要解决的技术性难题[8].例如：存取速度慢、效率低等.本研究根据前人的思想，采用排队论理论指导建立不同存取策略的数学模型，研究存取策略的作业方式，进一步缩短存取时间，对以后立体车库的研究有着深远的指导性意义.

1 立体车库的结构模型及排队模型

1.1 立体车库的结构模型

如图1所示，立体车库的结构为6层n列立体车库模型，停车位分布在巷道两侧，通过巷道地面的牵引装置来引导堆垛机做横向运动.

图1 立体车库简易模型

巷道堆垛式立体车库主要由车厅、巷道、停车位、堆垛机和搬运器等机械构成，根据场地的大小和实际需求可以建立高度不同的多种结构形式的立体车库.

1.2 巷道堆垛式立体车库数学模型建立

将巷道堆垛式立体车库模型简化，如图2所示，车辆的存取分成X轴，Y轴方向简易搬运坐标.车辆通过出入口进入到巷道，由堆垛机进行搬运至空闲的停车位，X轴方向负责堆垛机横向运动，Y轴方向负责堆垛机在巷道进行竖直垂向运动，即对堆垛机搬运存取车辆所在车库的相同层数a，堆垛机垂直升降运动所在层数为b，因此，可将简化的二维模型用坐标(a,b)来表示当前停车位置.

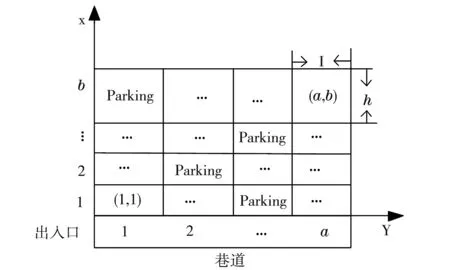
图2 立体车库数学模型

2 立体车库存取策略数学模型

2.1 存取车辆排队模型

对于车辆到达以后主要有两种排队方法，分为有限排队和无限排队.当顾客到达时，若停车系统达到饱和，系统自动关闭不再进入新的顾客则为有限排队；当顾客到达服务机构后对数量没有任何限制，按照一定顺序去排队被称为无限排队.车辆存取排队过程如图3所示，等待中的顾客选择相应合适的服务台进行车辆存取，最后服务结束后选择离开.

图3 立体车库排队系统

对于立体车库来说，车辆的存取时间以及汽车排队时间都可以看成符合泊松分布，根据泊松分布定义，则有:

(1)

研究在某段时间内(0，t)发生事件的概率,假设n=1,那么随机两辆连续到达的车辆通过概率整理得到公式(2).

P=e-λtλt，

(2)

其中N(t)表示,在单位时间(t0，t+to)内进行存取汽车数量；i表示汽车的数量，同时i满足是比零大的整数.λ表示汽车到达车库的平均时间概率.

2.2 存取车辆所用时间

当前坐标车位为(a，b)，下一目标车位为(a1，b1),上次执行的目标车位为(a2,b2),出入口坐标为(a0,b0).

出入口到当前停车位所用时间为：

t1=Max{t层|a-1|，t列|b-1|}+t出入.

(3)

(1)进行一辆车的存车所用时间为：

tC1=Max{t层|a1-a|，t列|b1-b|}+t出入+Max{t层|a-1|，t列|b-1|}.

(4)

(2)进行一辆车的取车时间为：

tQ1=Max{t层|a2-a|，t列|b2-b|}+t转+Max{t层|a-a0|，t列|b-b0|}+t出入.

(5)

2.2.1 存车优先策略

假设载车板从原点出发，到达当前位置为(a，b)，采用存车优先策略所需时间为：

tC2Q2=Max{t层|a-1|，t列|b-1|}+max{t层|a1-a|，t列|b1-b|}+t转+t出入+max{t层|a2-a0|，t列|b2-b0|}+t出入.

(6)

2.2.2 取车优先策略

tQ3C3=Max{t层|a1-a|，t列|b1-b|}+t转+t出入+max{t层|a-1|，t列|b-1|}+ max{t层|a1-a0|，t列|b1-b0|}+t出入.

(7)

2.2.3 顺序存取策略

tQ4C4=Max{t层|a1-a|，t列|b1-b|}+t出入+Max{t层|a-1|，t列|b-1|}+ax{t层|a2-a|，t列|b2-b|}+t转+Max{t层|a-a0|，t列|b-b0|}+t出入.

(8)

2.2.4 交叉存取策略

交叉存取策略共分为4种情况分别为：前一次取车，当前取车；前一次取车，当前存车；前一次存车，当前取车；前一次存车，当前存车分别进行分析.

(1)前一次取车，当前取车，下一辆存车所用时间为：

tQQ=Max{t层|a1-a|，t列|b1-b|}+t出入+max{t层|a-1|，t列|b-1|}+ax{t层|a2-a|，t列|b2-b|}+t转+max{t层|a-a0|，t列|b-b0|}+t出入;

(9)

(2)前一次取车，当前存车，下一辆存车的时间为：

tQC=Max{t层|a2-a|，t列|b2-b|}+t出入+Max{t层|a-a0|，t列|b-b0|}+t转;

(10)

(3)前一次存车，当前存车，下一辆为存车的时间为：

tCC=Max{t层|a-a0|，t列|b-b0|}+Max{t层|a1-a|，t列|b1-b|}+Max{t层|a-1|，t列|b-1|}+Max{t层|a1-a0|，t列|b1-b0|}+t转+t出入;

(11)

(4)前一次存车，当前取车，下一辆存车等待的时间为：

tCQ=Max{t层|a2-a|，t列|b2-b|}+Max{t层|a-a0|，t列|b-b0|}+t出入.

(12)

3 仿真及结果及分析

通过数据采集分析得到4种不同的存取策略的仿真结果分别如图5～7所示.由仿真结果可得知，在存车高峰期中，时间最短的为交叉存取策略，时间最长的为优先存取策略，运用交叉存取策略比优先存取策略用时减少21%左右.在取车高峰期中，时间最长的为优先存取策略，优先取车策略与选择交叉存取策略平均用时基本相当，运用交叉存取策略比优先取车策略用时减少28%左右.而在存取数量相当时进行存取车辆用时最长的是优先存车策略，用时最少的交叉存取策略比优先存车策略可节省32%左右.

综上分析可知，在存车高峰期、取车高峰期、存取相当三个时间段中，优先存车策略与优先取车策略相对来说耗费时间较长，两者的时间均高于交叉存取策略与顺序存取策略.在存车高峰期与取车高峰期中，顺序存取策略与交叉存取策略平均用时基本相当，用时最少的为顺序存取策略，相对耗时较少.当车辆存取相当时，交叉存取策略与优先存取策略较为适合，但考虑到若调整顺序无形增加了控制难度、运行管理等不定因素.所以采用顺序存取策略作为该立体车库的控制策略可以较大程度提高存取时间以及车库的运行效率.

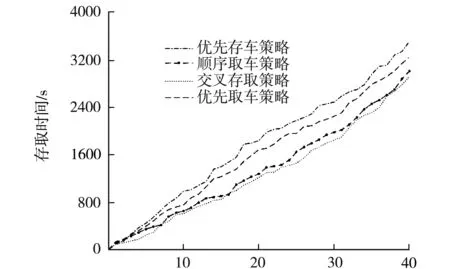
存取次数图4 存车高峰期仿真结果

存取次数图5 取车高峰期仿真结果

存取次数图6 存取相当时仿真结果

4 结 论

立体车库服务效率大多基于改进其存取效率，通过运用排队论分别建立优先存车、优先取车、顺序存取、交叉存取等不同路线，得到了较为理想的仿真结果，分析不同时间段的存取高峰期适当调整排队模型，有效地提高了立体车库的存取效率，减少了存取时间.对巷道堆垛式立体车库的研究有着深远的指导意义，具有良好的应用前景和社会效益.