基于Chebyshev逼近的分数阶谱微分算子矩阵
2021-04-09张光辉
张光辉
(宿州学院 数学与统计学院,安徽 宿州 234000)
分数阶微分方程作为一种新的建模工具,在弹性材料、信号处理、流体力学和控制系统等领域有非常广泛的应用[1-5].分数阶微分方程解的存在唯一性已被众多学者给出和讨论[6].下文将基于Chebyshev逼近,推导整数s阶和分数α阶谱微分算子矩阵,并建立用于计算α阶导数的Chebyshev谱微分算子矩阵的递推公式.
1 预备知识
定义1Caputo意义下的分数阶导数[7]:
(1)
其中a≤x≤b,m-1<α≤m,m∈N.

Tn(x)=cos(narccosx),|x|≤1.
(2)

引理1关于Caputo意义下的分数阶导数算子Dα,满足[7]:
Dα(λ1f1+λ2f2)=λ1Dαf1+λ2Dαf2,λ1,λ2∈R.
(3)
引理2n次Chebyshev多项式[8]Tn(x)=cos(narccosx),对∀n≥1,成立:
(a)Tn+1(x)=2xTn(x)-Tn-1(x),


2 Chebyshev谱微分矩阵的构建
2.1 整数阶谱微分矩阵
记区间[-1,1]上次数不大于n的所有代数多项式空间为:
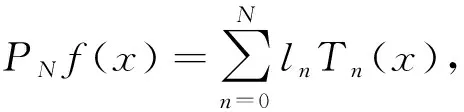
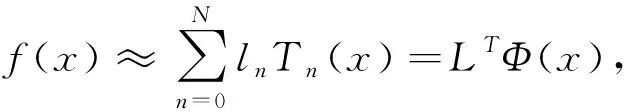
(4)
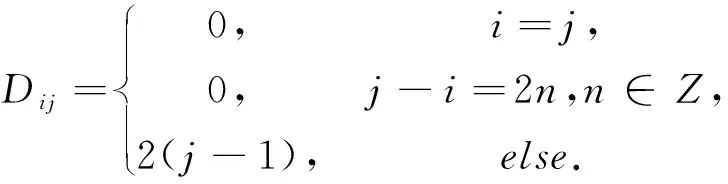
例如n=5时,(4)式为
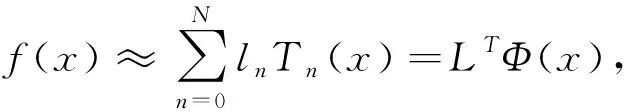
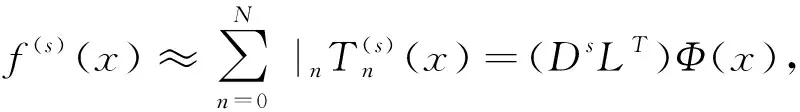
2.2 分数阶谱微分矩阵
当-1

(5)


(6)
其中J=[J0(x),J1(x),…,Jn(x)]|X,T=[T0(x),T1(x),…,Tn(x)]|X.

下面给出计算Jk(xi)的迭代公式,以完成矩阵J的计算[10].
定理1[-1,1]上由Chebyshev多项式Tn(x)生成的序列Jn(x)满足递推关系:
(1+x)1-α(-1)n+1,

考虑积分式
类似的,有
考虑积分式
由引理2(a)递推关系,进一步计算,得
整理,得
2.3 [0,T]上谱微分算子矩阵
当0 N图1 函数的阶Chebyshev谱导数精度 N图2 函数的阶Chebyshev谱导数精度 将用分数阶谱微分算子矩阵计算的数值结果和解析解进行比较,发现随着f(x)的Chebyshev级数展开式中截取项数n的增加,解析解和数值解误差的无穷范数迅速收敛,且在算例2中达到了谱精度,从而验证了谱微分算子矩阵的有效性和高精度.



3 数值实验


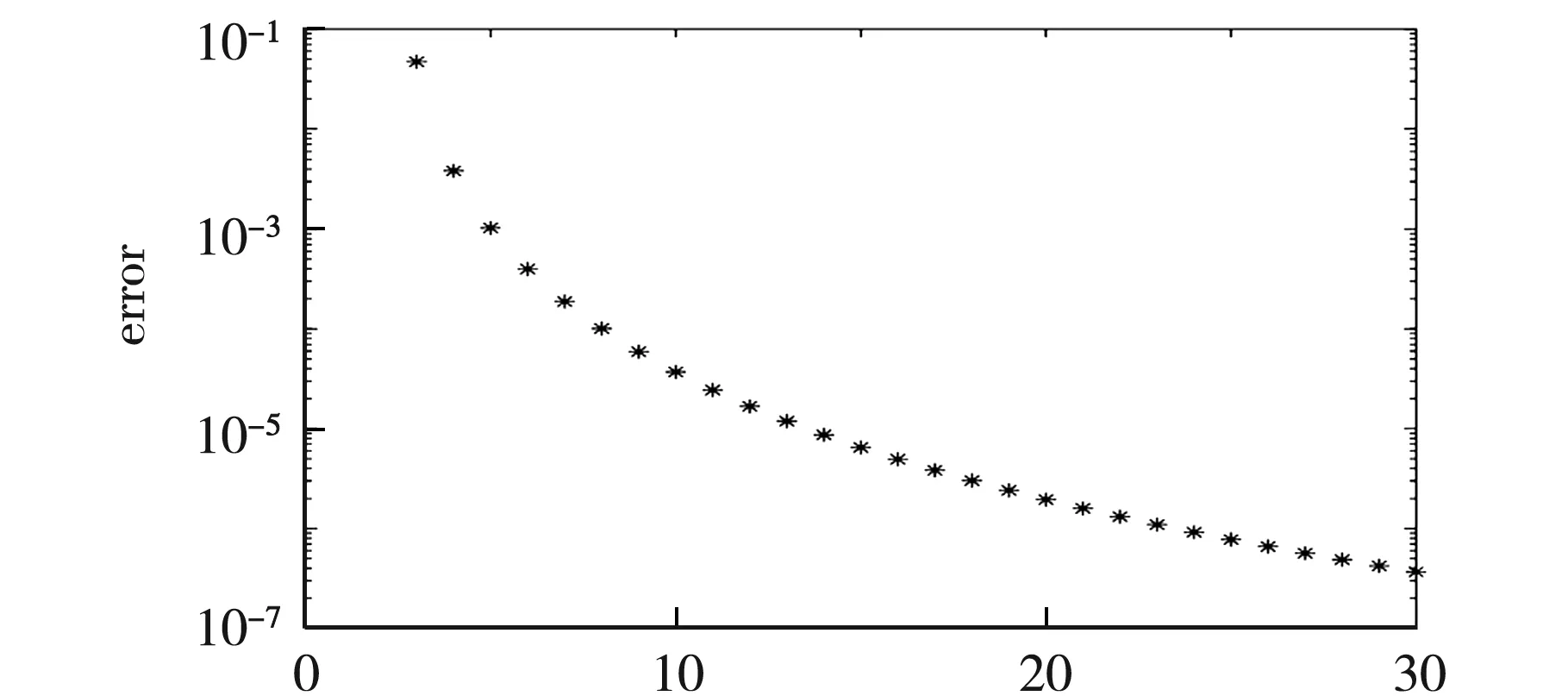


4 结 论
