基于频域幅值处理的扩频接收机抗干扰技术
2021-04-09赵彦雷
杜 丹,王 凯,赵彦雷
(1.陆军装备部驻石家庄地区第一军代室,河北 石家庄 050081;2.中国人民解放军32382部队,北京 100072;3.中国电子科技集团公司第五十四研究所,河北 石家庄 050081)
0 引言
扩频通信技术具有抗截获、抗干扰等很多优点,因而在各种领域得到了广泛应用。扩频增益提供了扩频体制系统足够的抗干扰能力,但当施加的干扰功率值超过系统的抗干扰容限时,会导致系统性能急剧下降以至于无法正常工作[1]。无线通信和导航系统中存在很多有意无意的干扰,随着电磁频谱资源的日益紧张,周边电磁环境也变得越来越恶劣。日益复杂的周边电磁干扰会影响接收机的正常工作[2],因此研究具有有效抗干扰能力的信号处理技术是非常有意义的工作。
本文以工作频段内存在多个干扰的情况为研究条件,提出了一种基于频域幅值信号处理的抗干扰处理技术[3]。根据统计学理论中的极限定理,当特定频段内存在多个干扰时,可以近似用高斯分布分析此时的观测噪声分布,多个干扰叠加在一起的概率密度也表现为高斯特性。此时,时域的幅值信号滤波处理就不能把多个干扰信号从高斯噪声中分辨出来,但是多个干扰的频谱与高斯白噪声的不同,因此,干扰信号加高斯白噪声在频域更容易检测和消除。
本文推导了局部最优检测的非线性函数,阐述了其工作原理;随后在导航接收机的二维捕获结构中采用频域幅值处理(Frequency Amplitude Domain Processing,FADP)技术,得到其检测器原理结构图;最后采用本文提出的FADP技术对高幅值的连续波窄带干扰进行抑制并仿真,而且仿真了将FADP应用在检测结构时的检测性能;最后得出结论:通过在传统的平方和检测器中添加FADP,能够提高伪码信号在强干扰条件下的捕获性能,提高了扩频系统的抗干扰能力。
1 局部最优检测技术
FADP技术是将幅值信号处理技术应用在频域,幅值信号处理技术是一种基于Neyman-Pearson和Capon研究基础的检测统计判决理论,其可实现结构由局部最优检测理论简化得到,主要在于判断统计量是信号和噪声的混合还是只有噪声的情况,下面定义2种假设:
(1)
式中,w[0]表示白噪声;s[0]表示有用信号。当H0为真时,若H1成立则认定为虚警情况,用PFA表示虚警概率P(H1;H0)。而采用检测概率表示漏警概率P(H0;H1)的补集1-P(H0;H1)。对于信噪比,虚警概率PFA,以及给定的观测数据长度,Neyman-Pearson检测器在此情况下是最优的,漏警概率P(H0;H1)被最小化了。其形式为:
(2)
右侧为此检测条件下的判决门限,左侧为最大似然估计检测统计量比。在扩频导航系统的实际应用中,经常存在接收端低信噪比的情况,此时接收到的信号是非常小的,深埋在噪声之下[4]。本文针对低信噪比情况下的检测器设计做了改进,使其在相比噪声信号很小的条件下达到最优。当设计系统具有一定的动态范围,信号存在较大的情况,该检测器也可以很好地得到应用[5]。因为首先需要保证微弱信号条件下检测器的性能达到最优,这是系统设计的前提。信号很强的条件下即使检测器的性能没有达到最优,也可以轻松检测到信号。出于以上考虑,专门针对低信噪比的应用条件,对上述幅值处理检测器进行适应性改进。2种基本假设为:
(3)
当H1为真实信号真实存在,x[0]的概率密度为Pθ(x),其中θ表示微弱信号的幅度,相比噪声它是非常小的变量,几近于0。当H0为真实信号不存在,x[0]的概率密度函数表示为P0(x)。∂Pθ(x)/∂θ在-∞
(4)
那么有:
(5)
式中,R1是n维采样空间中信号存在的判决域,相应地:
(6)
在式(2)~式(5)的前提条件下使得式(6)PD达到最大值。从式(6)看出,检测概率与信号幅值θ有关联。依据前面所做的规则性假设可得,在θ为很小的正数条件下,在θ=0处对PD进行一阶泰勒级数展开,可以得到:
(7)
PFA为已知参数,故需要PD(θ)的导数与R1有关,因此θ为任意值时,当且仅当PD(θ)在θ=0处的斜率最大,此时PD(θ)达到其最大值:
(8)
这就要在约束PFA为常数的条件下使斜率达到最大[7],Neyman-Pearson检测器就可在θ≈0的情形下被近似于:
(9)
设定一个滤波函数,通过在式(9)中应用链式规则,可以得到极其有价值的实现方式:
g(r)S>γ,
(10)
式中,S为接收信号作相关处理前的输入,可得:
(11)
本文的设计思想是在扩频导航系统中对局部最优检测方法进行适应性改进,采用非线性函数处理作相关前的接收信号再与相应的门限比较。将该方法应用于扩频系统的具体方式为:将观测序列经过局部最优的非线性函数处理后作为伪码相关器的输入[8]。相关器的输出结果与门限进行比较,实现了局部最优检测器。
2 应用FADP技术的信号捕获结构
在采用扩频体制的导航系统中,当多个窄带干扰信号存在接收到的信号中时,通过时域处理很难区分这些干扰,然而采用频域处理可能起到意想不到的效果。这些干扰大部分集中在特定的频率范围,采用频域的方法可能较容易处理。
本文提出的将频域幅值处理方法应用于扩频导航接收机,对于抑制导航系统接收到的多窄带干扰效果是非常明显的。
在扩频导航系统接收端,观测量信号为:
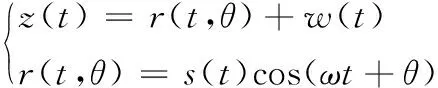
(12)
式中,r(t)为经过调制的有用导航信号;s(t)为导航电文信息;w(t)为高斯白噪声(可能存在干扰),信号相位θ均匀分布于[0,2π]区间。导航信号的检测在于判断观测量描述为z(t)=r(t,θ)+w(t)还是描述为z(t)=w(t)。对输入端的AD采样信号进行正交变频或正交变换得到I和Q两路正交信号,再对2路信号分别使用局部最优的非线性函数g(xi,yi),这个函数通过局部最优检测理论[9]得到,表示为:
(13)
式中,fnn是2路正交信号的联合噪声分布函数。
由于在实际应用中,扩频导航系统接收端观测噪声的概率密度函数(Probability Densinity Function,PDF)一般简化为加性高斯白噪声。此时捕获环路采用相关累加器方式,这是优先采用的检测方法。但是实际观测噪声一般为非加性噪声,采用相关累加器的捕获方式在非加性噪声情况下检测信号的性能会下降以至于无法检测到信号[10]。因此,观测噪声的PDF估计至关重要,是研究在未知信道模型中设计最佳捕获结构的关键。连续多项式近似算法和离散柱状图统计方式是2种常用的PDF估计方式。由于离散柱状图统计方式计算量相对较少,执行结构相对简单,所以本文采用此方法来估计噪声的概率密度估计[11]。但由于离散柱状图统计方式得到的PDF是基于实时统计估计的,因而是离散的,解决方法是增加滤波环节来平滑得到PDF[12]。
上面I和Q两支路检测结构实现起来难度较大,原因在于实时统计估计I和Q两个独立支路的联合噪声分布函数fnn是非常困难的。但是FADP技术提高跟踪环路输入信噪比(SNR)的本质在于依据统计判决理论对接收信号的幅度作非线性优化处理,接收信号是包括多个干扰信号和有用信号的混合信号。对接收信号的幅值R作非线性处理,需要将最优检测函数的应用从直角坐标系转换到极坐标系[13],非线性函数应用于信号幅值的检测回路原理如图1所示。
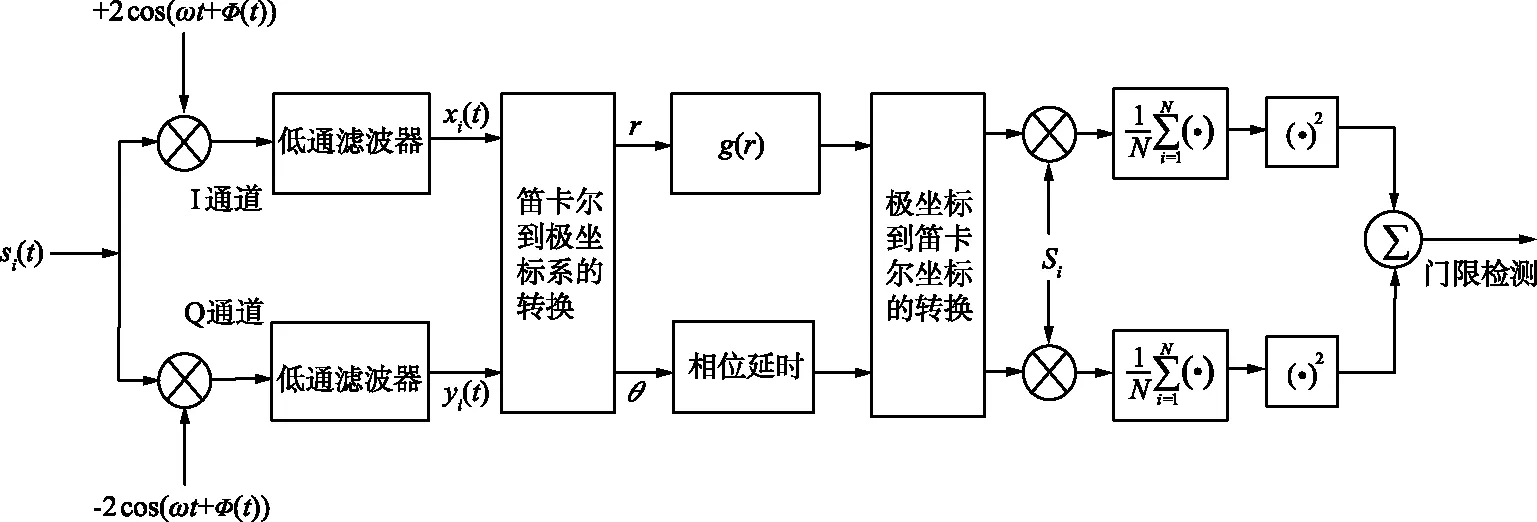
图1 非线性函数应用于信号幅值的检测回路原理Fig.1 The introduction of non-linear functionto amplitude domain detection loop
经过正交变换或正交变频的2路正交信号,被变换成幅度R和相位θ的形式。经过极坐标处理的非线性幅值信号处理函数可以表示为:
(14)
这个非线性函数基于输入信号幅值的概率密度函数得到。在扩频导航系统中输入信号相对于干扰和噪声非常小,深埋在干扰和噪声之下,所以信号幅值的概率密度函数近似干扰加噪声的概率密度函数。时域幅值处理滤波器对于高斯白噪声和扩频导航信号是透明的。根据统计学理论中的中心极限定理,很多窄带干扰出现的频谱可以近似表示为高斯分布,叠加信号的概率密度函数呈现高斯特性,此时采用时域幅值处理滤波器不能从高斯噪声中识别出多个干扰信号,但是采用频域手段能够检测出多个干扰信号,因为这些干扰信号的频谱和高斯噪声完全不同,通过FFT可以分辨时域上难以区分的多非高斯干扰[14]。采用FADP技术的具体过程为:首先对输入信号进行FFT变化,再进行幅值信号处理滤波,最后通过IFFT变换处理后的信号,此时干扰信号已经被抑制[15]。
FADP是在频域使用幅值信号处理,特点在于将信号处理从时域转换到了频域,利用FADP的框图如图2所示。

图2 FADP的执行结构Fig.2 The implementary structure of FADP
频域幅值信号处理滤波器既可以用于实信号,也可以用于复信号。对于实信号,可以直接将非线性函数g(r)应用于实信号;对于复信号,需要把信号从直角坐标系转换到极坐标系。频域幅值处理滤波器采用FFT模块完成复信号到频域的变换[16-17]。
GPS等导航系统采用扩频体制,有用信号的频谱被伪随机码扩展成宽带信号,呈零均值状态。在变换为频域信号后的噪声PDF仍保持零中心的高斯分布,但是将其从直角坐标转换到极坐标后其分布将改变[18]。对于I和Q正交通道的信号,若R为幅度值,则:
(15)
常见高斯白噪声的幅值概率密度表达如下:
(16)
有以下2个统计性质:
(17)
(18)
如果化简上面卷积可得到:
(19)
进行如下的变量替换:
(20)
式(19)变为:
Kexp(-u/2),
(21)
式中,K是常量,带入式(18)可得:
(22)
从式(22)看到,在变换到频域以后接收信号的PDF呈现开方分布,改变了原来高斯分布的特性,此时的滤波器为非线性滤波器。非线性处理函数经过重新计算得到:
(23)
此时非线性函数g(r)在频域上呈现零附近发散状态,故通过转换FFT后的信号从而得到呈高斯分布的PDF。具体实现方法为在FFT变换后加上一个复常数C,从而实现将频域PDF到频谱轴上较大位置的迁移[19]。通过添加复常量来实现将计算后的信号模值迁移到|C|附近,选取C=90+90i,经过卷积运算后得:
(24)
为了保持接收信号高斯分布的对称性,需要选取一个离零点足够远的常数,本次设计的主要工作在于将FADP技术应用到扩频系统的平方求和检测器中,从而大大提高了扩频导航接收机的抗干扰能力,传统平方和检测结构应用FADP原理如图3所示。
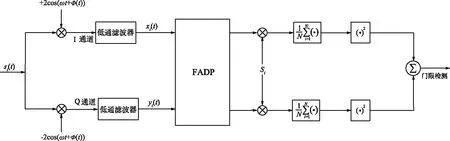
图3 传统平方和检测结构应用FADP原理Fig.3 The application of the FADP in the traditional quadrature detection loop
3 仿真分析
3.1 信号产生
本算法的应用环境为典型扩频导航系统,充分考虑与应用场景的一致性,选用GPS信号L1频点中的C/A码产生仿真信号。GPS C/A码也叫粗码,是一种gold码,采用2个M序列产生。伪码周期为1 023个码片,码速率为1.023 MHz,因此一个伪码序列周期为1 ms,设计采样周期为20 MHz。
作为伪随机信号,理论上讲对其进行傅里叶变换是不满足条件的,不能对它进行FFT,所以采用功率密度谱来表征其频域信号结构,功率密度谱也就是单位频率内的信号功率[20]。
3.2 仿真结果及分析
先将接收信号转换到频域再进行幅值信号处理,采用FFT和IFFT方法计算数值,从而将频域变换的复杂度从传统DFT的N2降到N*logN。N为数据点长度,N=1 024。
针对扩频系统常见的强功率的脉冲干扰(PWI) ,对其进行干扰抑制,该干扰是最常见的一种干扰,下面主要对比了强功率的脉冲干扰的频率幅值处理的输入输出功率密度谱,如图4所示。
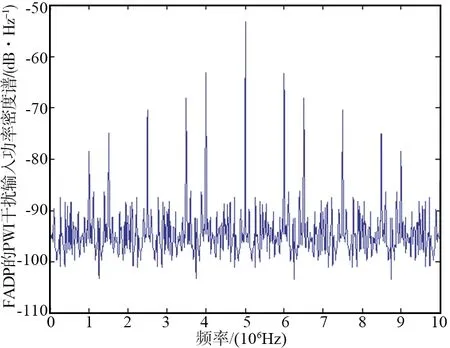
(a) 频域幅值处理前的脉冲干扰频谱图
由图4可知,图4(a)是在没有经过频域幅值处理的脉冲干扰频谱图,图4(b)是脉冲干扰经过频域幅值处理之后的频谱图,因此可以清楚地看出,窄带干扰信号经过FADP,脉冲干扰得到了很好的抑制,其功率密度谱基本上只剩下了热噪声信号。
本文方法的最终应用是将FADP添加到现有的扩频信号捕获结构中和扩频系统的抗干扰性能和信噪比,使系统能更好地检测到信号。该方法把输入信号的特性从开方分布重新变换到传统的高斯分布,能够提高系统在多个强窄带干扰情况下的检测概率。将频域幅值信号处理技术应用在检测结构中,其检测性能如图5所示。

(a) 未经过频域幅值处理的相关峰曲线
图5(a)是没有FADP措施的检测器,图中很多伪峰的相关值很高,已经无法识别真实信号;图5(b)是采用FADP技术的检测器,可以很容易检测真实信号,多个窄带干扰已经被有效抑制,信号几乎没有损失。
4 结束语
本文在频域引入幅值信号处理算法,在处理之前先将信号变换到频域,经过幅值信号处理再转换回来,形成了FADP算法。FADP算法在频域具有良好的分辨能力。针对扩频系统进行常见干扰样式抑制效果仿真,可见FADP对于脉冲干扰有很明显的抑制效果,而对有用信号的损失相对较小,衰减小于3 dB。通过在传统的平方和检测器中添加FADP算法,能够提高扩频系统的抗干扰能力,提高伪码信号在强干扰条件下的捕获性能。
