涂层下金属管道缝隙腐蚀瞬态的数值模拟

白浩然,饶永超,王树立,孙 琪,李立军,贾 茹

(1. 常州大学 石油工程学院,常州 213164; 2. 榆林学院 化学与化工学院,榆林 719000)

现阶段，石油与天然气主要通过埋地管道进行长距离输送，管道腐蚀是威胁其安全运行的最重大因素之一。对于埋地金属管道，国内外主要采用涂层和阴极保护技术二者结合的方法来防止其腐蚀[1-2]。然而在管道安装过程中，由于管道补口喷涂和不可避免的机械损伤等可能会使管道涂层出现缺陷,在埋地环境中缺陷处受到侵蚀，随着时间的推移缺陷处的涂层可能失效并在管道表面形成狭窄的缝隙[3]。腐蚀介质(气体、电解质、含硫微生物等)进入缝隙可能引发缝隙腐蚀，进一步加快管道腐蚀，缩短管道寿命。目前,世界公认最有效的管道防腐蚀方法是在管道表面施加阴极保护，但是在涂层下，缝隙内腐蚀过程主要取决于离子的传质和电化学反应。由于缝隙宽度过于狭窄，现有的测量探头或电极无法深入缝隙内[4]，现阶段关于缝隙内电位分布和传质过程的理论研究仍然有限，缝隙内阴极保护作用机制仍是一个有争议的问题[5]。通过试验了解缝隙腐蚀以及阴极保护的有效性是远远不够的。数值模拟技术日益完善，可以高效对数据进行分析，大大提高了缝隙腐蚀的理论研究效率。

现如今国内外学者对缝隙腐蚀的数学模型已经进行了大量的研究[6-9]。例如， KENNELL等[10]提出了一种结合临界缝隙解理论(CCST)和IR降理论的一维稳态缝隙腐蚀模型，认为物质的传质和电位在缝隙内外都会下降，阴极反应很可能发生在缝隙口处。XIAO等[11]建立了定量相位模型研究盐水中铁的缝隙腐蚀，考虑了六种离子和一些相关的化学反应，分析了不同电位下与腐蚀相关的理化性质。但是相当多的研究只针对稳态下缝隙腐蚀的形成机理和化学状态，且侧重于没有阴极保护条件下缝隙腐蚀的潜伏期及其发展过程,而对瞬态条件下缝隙腐蚀过程的研究还不够充分，且有无阴极保护条件下,缝隙腐蚀的电化学过程完全不同。SONG[12]针对可变缝隙(即间隙随着缝口距离变化而变化)开发了一种预测管道化学性质的数学模型,在有(无)阴极保护两种条件下，探究了管道表面缝隙中化学反应和腐蚀速率的变化。CHEN等[13]和WANG等[14]开发了在阴极保护条件下的缝隙腐蚀模型，以研究瞬态的电化学过程，但两种模型都只考虑了x方向的数值变化。近些年来新开发的瞬态模型，大部分都只考虑一个维度(即忽略宽度对电位和化学参数的影响)。因此，针对有阴极保护的缝隙腐蚀，研究其瞬态的化学状态，同时尽可能在空间维度上贴近实际，分析其局部溶液环境中的电化学过程，得到更加准确的模拟结果，对研究阴极保护机理以及防止涂层下的金属腐蚀十分重要。

本工作主要在前人工作基础上，建立了一个二维瞬态模型,研究涂层下施加阴极保护的缝隙腐蚀，综合考虑了缝隙内离子传质、化学反应和水电离等问题，利用有限元软件模拟涂层下缝内环境中化学和电化学的瞬时状态，并根据模拟结果分析缝隙腐蚀的阴极保护机理，为研究缝内腐蚀过程提供了理论依据，并将模拟结果与试验结果进行对比，以期确定合理的阴极保护电位，优化管道的防护措施，从而减轻管道腐蚀，节约成本，防止在使用过程中管道发生灾难性事故。

1 理论研究

1.1 几何模型

由于缝隙腐蚀是一个复杂的电化学过程，在模拟过程中会进行近似假设和简化,如图1所示。该模型在缝口处添加一个电解质域，避免模拟时电解质的电位边界与电极表面相连接，从而防止电位梯度奇点导致的迭代步数收敛。缝口坐标(0,0)为起点，缝宽(δ)1 mm，缝隙深度(L)200 mm。

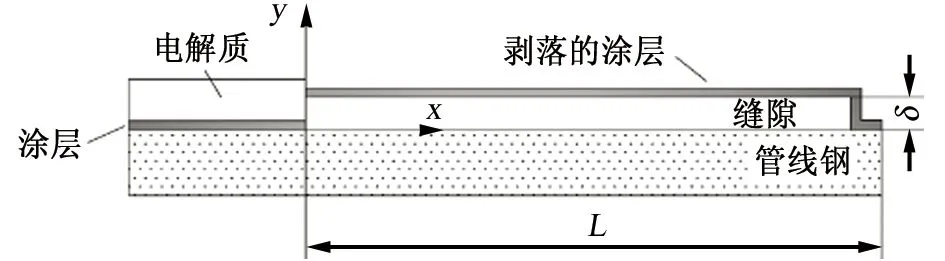
图1 缝隙腐蚀几何模型Fig. 1 Geometry model of crevice corrosion

1.2 模型条件

模拟电解质溶液为经过土壤地下水稀释的Na2SO4溶液，根据无限稀释理论的基本假设，模型中电解质域内为无限体积的Na2SO4溶液，且溶液中的化学物质含量是恒定不变的。缝隙内外溶液被空气饱和，在施加阴极保护电流的情况下，氧气会从缝口进入缝隙内部且被不断消耗。除此之外，为简化模型，还进行了如下假设：

(1) 在施加阴极保护电流的情况下，缝隙内阳极溶解反应受到抑制，缝内主要反应为氧气还原反应，且缝隙内溶液变为碱性溶液，反应式如下：

(1)

(2) 缝内溶液处于停滞状态，并且由于缝隙宽度过于狭窄，化学物质对流忽略不计，在缝隙内化学物质通过扩散和电迁移进行传质；

(3) 传质过程考虑四种化学物质：OH-、SO42-、Na+、O2；

(4) 在初始状态下缝隙溶液中各化学物质的浓度沿x和y方向均匀分布，反应过程中缝隙宽度不变，且不考虑沉淀和管道钢表面的腐蚀形变；

(5) 化学物质传质过程满足纽曼电中性原则[15]：

∑zici=0

(2)

式中：i是溶液中的化学物质;ci是浓度(mol·L);zi是电荷数；

(6) 模型考虑到水的电离平衡:

c(OH-)c(H+)=Kw

(3)

-lgKw=14.94-0.042 09(T-273.15)+

0.000 171 8(T-273.15)2

(4)

Kw=10-lgKw

(5)

式中:Kw为水的离子积常数;T为温度。

(7) 金属表面的电双层厚度足够小，可忽略不计。

1.3 反应方程式

1.3.1 传质方程

在缝隙内，化学物质的运输受到三种机制控制：离子电迁移、扩散和对流。化学物质i的质量流量(Ni)由式(6)给出[15]：

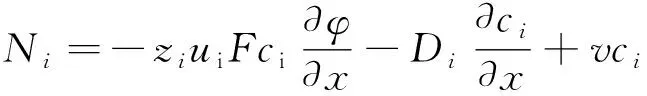
(6)

式中：Ni是i的质量流量(mol·cm-2·s-1)；ui是迁移率(m·V-1)；F是法拉第常数(96 500 C·mol-1)；φ是缝隙内钢的局部电位(V)；Di是扩散系数(cm2·s-1)；v是对流速度(m·s-1)。

因此，在等式的右侧存在第一迁移项，第二扩散项和第三对流项。

假设模型为静态，对流速度为零。因此，缝隙内的质量流量可写成如下形式[15]：

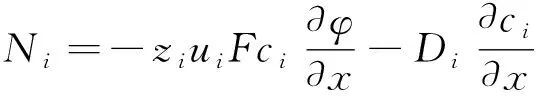
(7)

在以往的研究中，一般只考虑沿缝隙x轴方向的反应[16-18]。在本模型中，考虑了沿x和y轴的二维传质和堆积效应。如图2所示，当离子以恒定速度从x1移动到x2、从y1移动到y2时，其净流量为[19]：

ρividydz|x+dx-ρividydz|x+ρividxdz|y+dy-

ρividxdz|y=nidydz|x+dx-nidydz|x+

nidxdz|y+dy-nidxdz|y

(8)

式中：ρi是密度(kg·m-3);ni是质量速度(kg·m-2·s-1)。

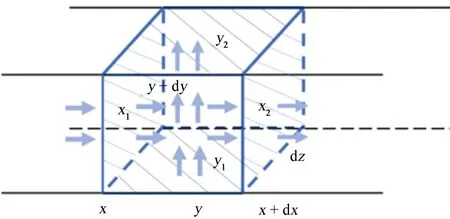
图2 二维传质积累示意图Fig. 2 Diagram of 2D mass transfer accumulation

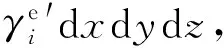
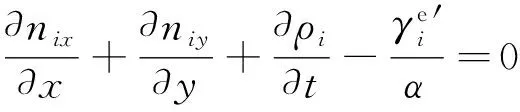
(9)

式(9)可以用摩尔表达，可得式(10)：

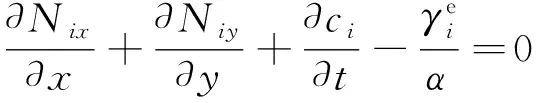
(10)

式中：Nim为m(m=x,y)方向上i的摩尔通量(mol·m-2·s-1)。

由于以上所述可以忽略对流效应，根据能斯特-普朗克方程，离子的质量流量Ni为：

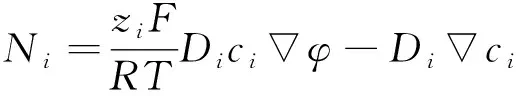
(11)

缝内质量守恒方程可以表示为[13]：

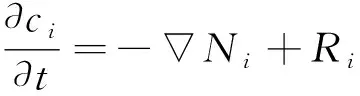
(12)

式中：t为时间(s);Ri为化学反应中i产生或者消耗的速率，主要为氧气的还原反应，有：

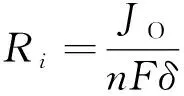
(13)

式中：JO是氧气交换电流密度(A·cm-2);n是电极反应的化学计量系数。

因此式(12)可以如下表示：

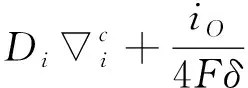
(14)

1.3.2 电化学动力学方程

缝隙中氧还原由电化学控制扩散[13]：

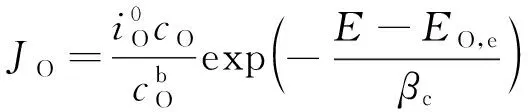
(15)

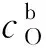
因此式(12)、(13)可以写成：

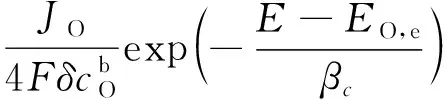
(16)

1.4 初始条件与边界条件

1.4.1 边界条件

根据以往学者的研究，在缝隙口处所有化学成分是恒定且不随时间变化的，而应用的阴保电位可以作为固定值给出[20]。

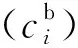
(i=O2,OH-,SO42-,Na+,0≤x≤L,0≤y≤δ)

(17)

在x=0处，所有化学物质的浓度与本体溶液化学物质的浓度相同，并且电势与施加的阴极保护电势(Ecp)相同：

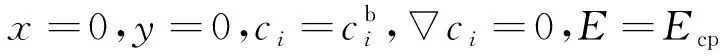
(18)

在x=L处，因为没有物质穿过边界边缘，缝隙的末端和所有物质的通量均为零：

x=L,ci=0,E=0

(19)

1.4.2 初始条件

根据矩形二维缝隙，结合以往研究得到阴极保护下缝隙腐蚀的数学模型，以1.2节所叙述的模型条件和电解质的理化性质为基础，同时利用PARSTAT 2273电化学工作站测定极化曲线，拟合曲线获得X70管线钢的阴极塔菲尔斜率以及交换电流密度，如图3所示。本体溶液为0.01 mol·L-1的Na2SO4溶液。基于无限稀释定律，缝隙外的本体溶液含量恒定且体积无限大。pH受阴极电流和本体溶液的影响。表1为初始条件。

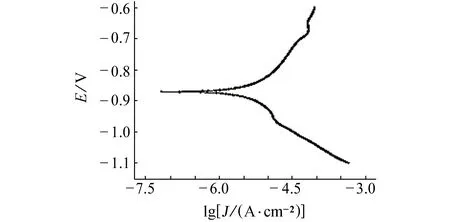
图3 X70管线在土壤中的极化曲线Fig. 3 Polarization curve of X70 pipeline in soil

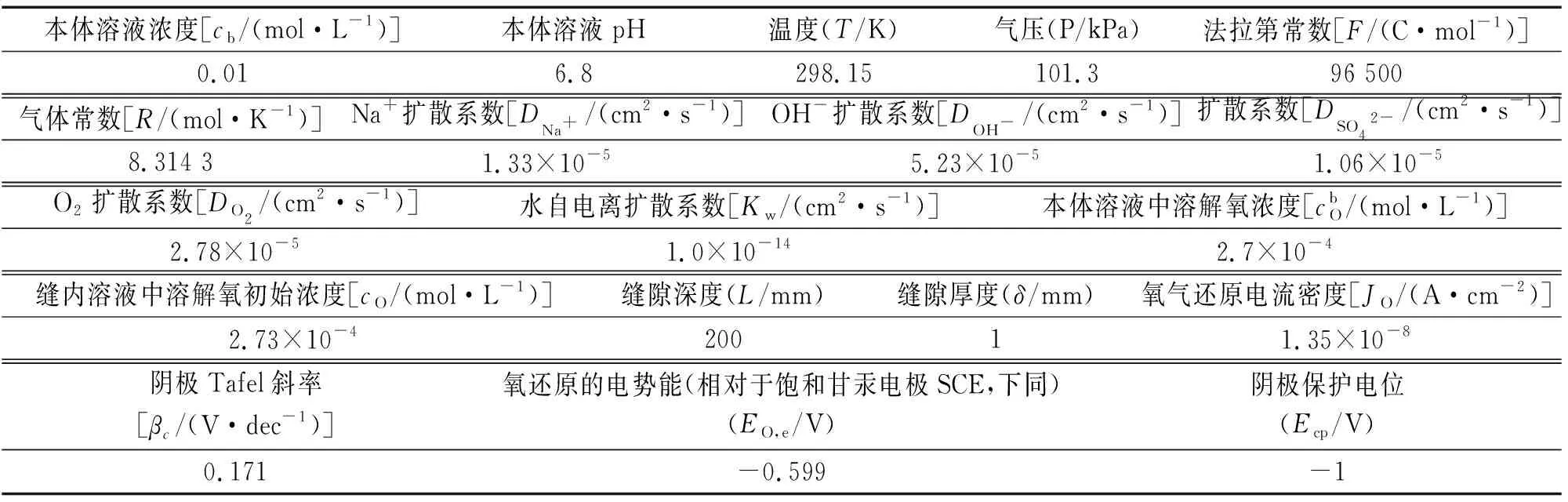
表1 初始条件Tab. 1 Initial conditions

1.5 数值处理

式(12)、(14)是一组非线性的二阶偏微分方程，需要相互关联[21]。然而在方程中，ci和E相互耦合，不可能有解析解，但是可以得到数值解。所以数值模拟技术可以解决此类问题，有限差分法(FDM)因其剖分简单、编程计算方便，通常用于求解具有数值解的偏微分方程。首先，将方程和初始边界条件做无量纲化处理；其次，剖分网格、划分时间差量；最后，通过数值迭代求解方程[13]。方程由有限元软件Comsol求解,Comsol对模型几何体的网格划分灵活，由于缝隙口附近电位梯度和浓度梯度很大并且传质效应显著，所以网格尺寸需要足够小，以获得准确的模拟结果。同时考虑水的自电离效应，选用水基电中性环境防止缝口处电位梯度奇点导致迭代步数收敛，将本体溶液进行区域化，缝隙外电解质的电位边界与管体表面氧化还原反应边界不接触。

2 结果与讨论

2.1 缝内电位分布

由图4可见，缝口处的电位和阴极保护电位大致相同，均为-1 V，随着时间的推移，延缝隙每个点的电位均向正方向移动。同一时间点下，缝隙深处的电位要高于缝口处的。100 h后，缝隙最深处的电位最值为-0.79 V，低于埋地管道最低保护电位-0.85 V。根据模拟情况分析，在100 h内缝口处可以完全被阴极保护电流覆盖，随着缝隙深度的增加和时间的推移，阴极电流逐渐向缝内流入，由于缝隙的特殊性和溶液的IR降(存在于管道和电解质电位测试过程中的电压降)下降,阴极电流无法到达缝隙最深处。缝隙内部和外部的电位梯度随着时间的延长逐渐减小。从模拟结果来看，缝隙深度超过约150 mm后，阴极保护电流将无法生效，缝隙内部的电场呈阴性，因此阴离子(SO42-)迁移出缝隙，缝口处的电位梯度比缝内的高，且阴离子迁移率远高于缝内的。

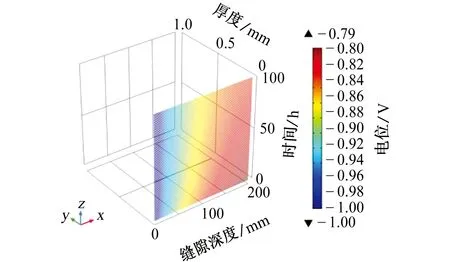
图4 电位与缝隙深度随时间的变化Fig. 4 Variation of potential and crevice depth with time

2.2 缝内溶液pH

溶液pH受cOH-的影响，OH-在缝隙内的运动方式主要为扩散和电迁移，这受到缝隙形状和极化电流的制约[22]。其扩散的主要形式是从缝内向缝口部分扩散，电迁移速率反应为电位梯度的大小，电位梯度高，OH-的迁移速率越高[23]。pH与cOH-的关系式如下：

pH=14+lg(cOH-)

(20)

如图5和图6所示，缝隙中每个点的pH随着时间的延长而增加，在施加极化电流后的5 h之内，溶液的pH迅速从6.8升高到10以上；随着时间的继续延长，溶液pH逐渐稳定。溶液pH随缝隙深度的增加而升高，约100 h后其pH稳定在12左右，在距离缝口约15 mm处溶液pH出现峰值。

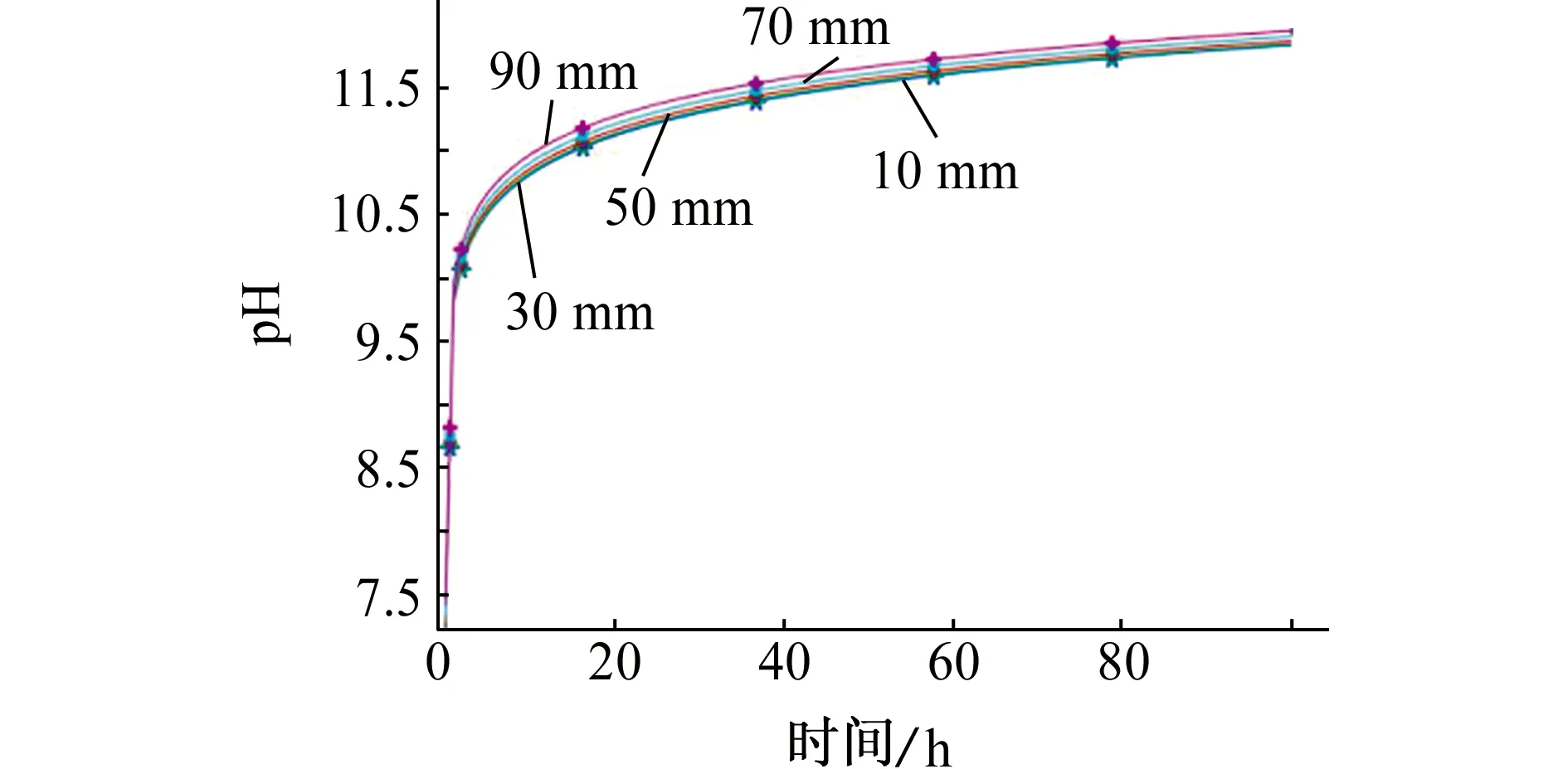
图5 至缝隙口不同距离处溶液pH随时间的变化Fig. 5 Variation of solution pH with time at different distances to the crevice mouth

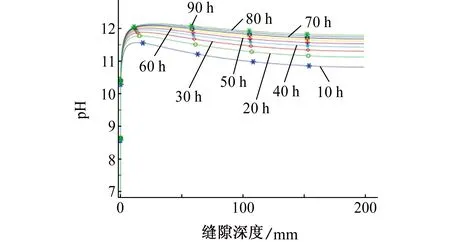
图6 不同时间下溶液pH随缝隙深度的变化Fig. 6 Variation of solution pH with crevice depth at different times

从以往的研究结果来看，由于缝口处离子的电迁移和扩散效应方向相同，缝口处的浓度梯度和电位梯度比缝内的要强很多，阴离子要用更慢的速度达到稳定值。而缝内溶液中离子的扩散和电迁移方向相反，缝隙越深浓度梯度和电位梯度越小，溶液pH可以达到更高[20]。由图6可知,由于缝口处发生还原反应，氧气浓度降低，OH-浓度迅速升高，而缝隙内过于陕窄，传质效应在缝内受限，所以缝隙口附近的溶液pH比缝隙内的变化更快，故缝隙内溶液pH会更快达到稳定值而不再变化。

2.3 溶解氧浓度分析

缝内溶液pH主要受溶解氧(DO)的影响，缝隙内的氧气主要被钢表面发生的还原反应消耗。在模拟过程中，氧气的还原反应是影响腐蚀速率的最重要因素，氧气还原速率直接影响金属的腐蚀速率，如图7所示。

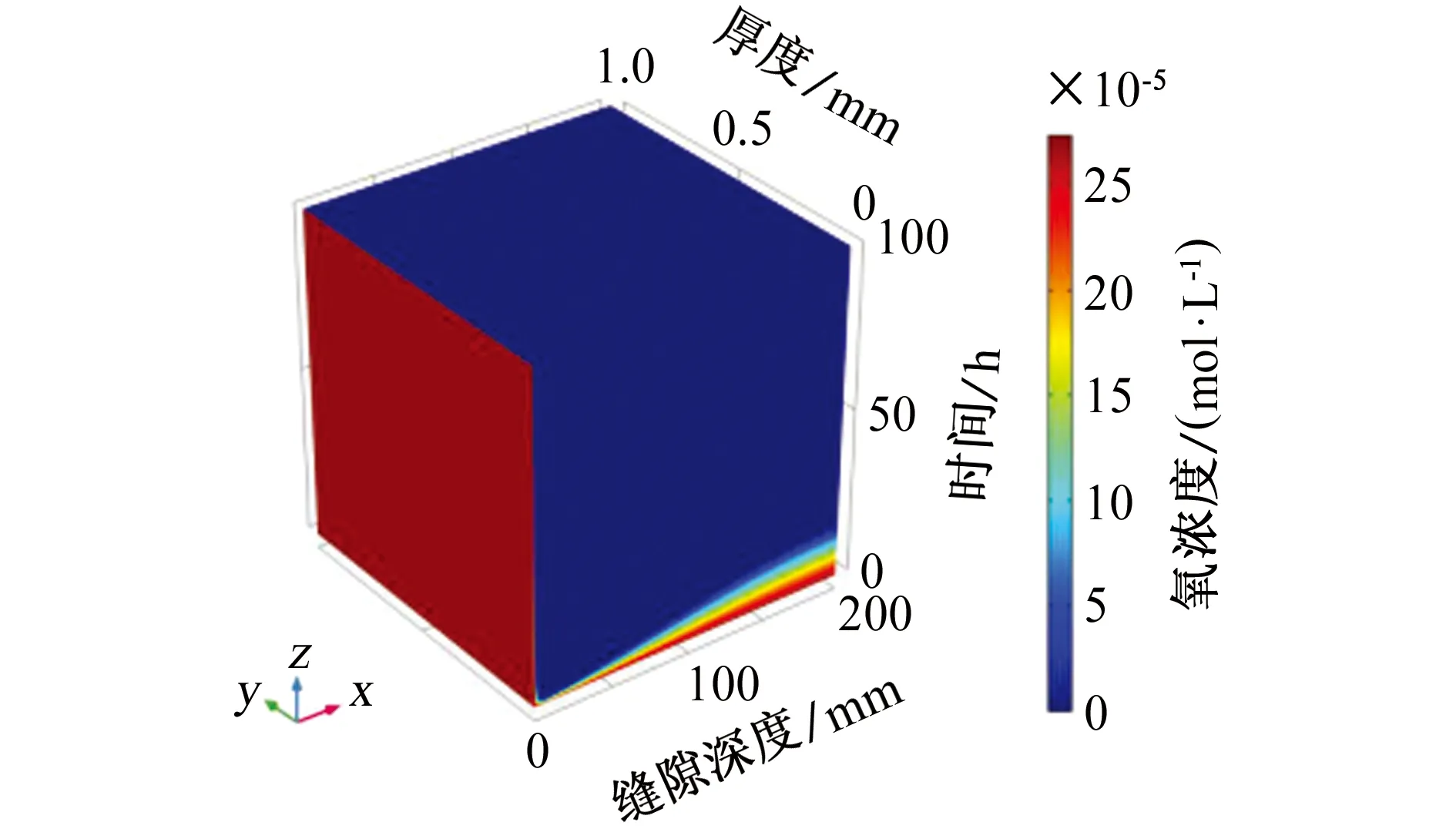
图7 缝内溶解氧浓度随时间和深度的变化Fig. 7 Variation of dissolved oxygen concentration in the crevice with time and depth

由图7可以看出，在缝口处溶解氧浓度没有发生变化，这是因为外部溶液为无限稀释溶液，氧气可以从外部溶液中不断得到补充。在缝隙中由于氧气被还原反应消耗，缝口处的氧气在较短时间内被消耗，缝内溶液中溶解氧的消耗速度远大于氧气扩散的补充速度，溶解氧浓度随着时间的推移而急剧下降。这是阴极保护效应开始时溶解氧浓度分布的一个典型现象。随着缝隙深度的增加，缝内溶解氧消耗的速度逐渐变缓，这是由于只有少量的氧气扩散到缝隙深处，并且缝隙深处还原反应速率比较低，当溶解氧消耗殆尽时，外部氧气无法及时扩散到缝隙深处，这和以往的试验研究结果相同。

2.4 电化学影响下的缝内离子浓度

由于缝隙内只存在氧气的还原反应，并且产生OH-，溶液中的阴离子和阳离子会发生迁移以保持电中性原则。如图8所示，可以更直观地展现出金属阳离子在溶液中的浓度变化情况。模拟结果表明，在距缝口约30 mm处Na+浓度达到峰值，约为外部溶液浓度的6.6倍，随着缝隙深度的增加，Na+浓度急剧降低，在缝隙最深处Na+浓度的最小值和缝隙外部的保持一致。缝隙深处由于缝隙过于狭窄，Na+的扩散速率急剧降低，因此无法向缝内传质，Na+的迁移导致阴极电流无法到达缝隙深处，影响了阴极保护的效果。

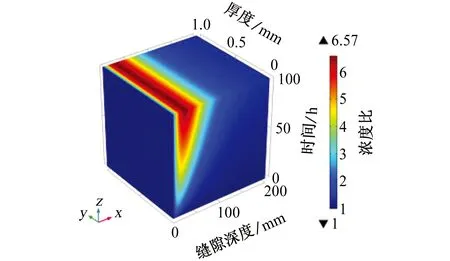
图8 缝内Na+浓度与初始条件下Na+浓度的比值随时间和缝隙深度的变化Fig. 8 Variation of the ratio of Na+ concentration in crevice to Na+ concentration under initial condition with time and crevice depth

根据电中性条件的假设，随着缝隙内OH-浓度的增加，SO42-应向缝隙外部迁移，从图9中可以看出，缝隙深度为0～25 mm，SO42-浓度比下降到0.3以下，最低值为0.12。可见阴离子浓度受传质效应控制，缝隙口的电位梯度大，并且缝口与缝隙外部溶液中离子的扩散传质受缝隙形状影响较小，所以SO42-浓度迅速下降。在缝隙深处由于受到环境限制，SO42-浓度变化较慢。

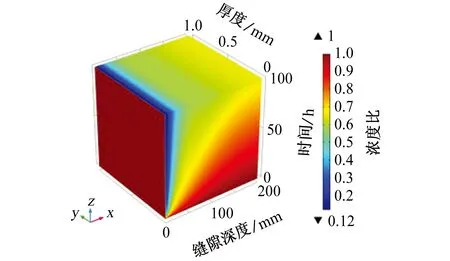
图9 缝内SO42-浓度与初始条件下SO42-浓度的比值(简称浓度比)随时间和缝隙深度的变化Fig. 9 Variation of the ratio of SO42- concentration in crevice to SO42- concentration under initial condition with time and crevice depth

根据以往的模拟和试验结果，由于溶液保持电中性，Na+向缝隙内部迁移，同时向缝隙外部扩散，Na+浓度与OH-浓度近似相等[24-25],这与本模型的模拟结果基本一致。

2.5 溶液电导率的影响

模型中电导率(σ)可以用如下方程表示[15,26]：

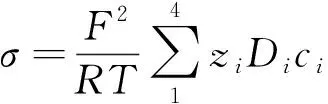
(21)

从上式中了解到，溶液的电导率与阴阳离子浓度密切相关，从图10中可以直观地看出缝内溶液电导率的变化，缝隙中电导率整体呈现上升趋势，且随着时间的增加而增加、随深度的增加而减小,这与WANG等[14，27]的试验结果相一致。根据前面章节的数据分析，由于缝隙内发生了氧气的还原反应，造成了OH-浓度的升高，为了保持缝内溶液的电中性，阳离子(Na+)向缝内迁移，阴离子(SO42-)向缝外扩散，因此在缝口处的离子传质运动剧烈，造成电解质溶液电导率大大增加，最大值约为本体溶液的4.2倍。但是缝隙底部的电位梯度和电流密度远远小于缝隙口附近的，所以电导率虽然因离子的传质而增加但是远没有缝口附近电导率增加的快。与此同时，由于受到缝隙形状和电位梯度的限制，Na+和SO42-只能在距缝口大约100 mm有限距离内进行传质运动。综上分析可知，电解质电导率的模拟结果与前几节得到的结果一致。

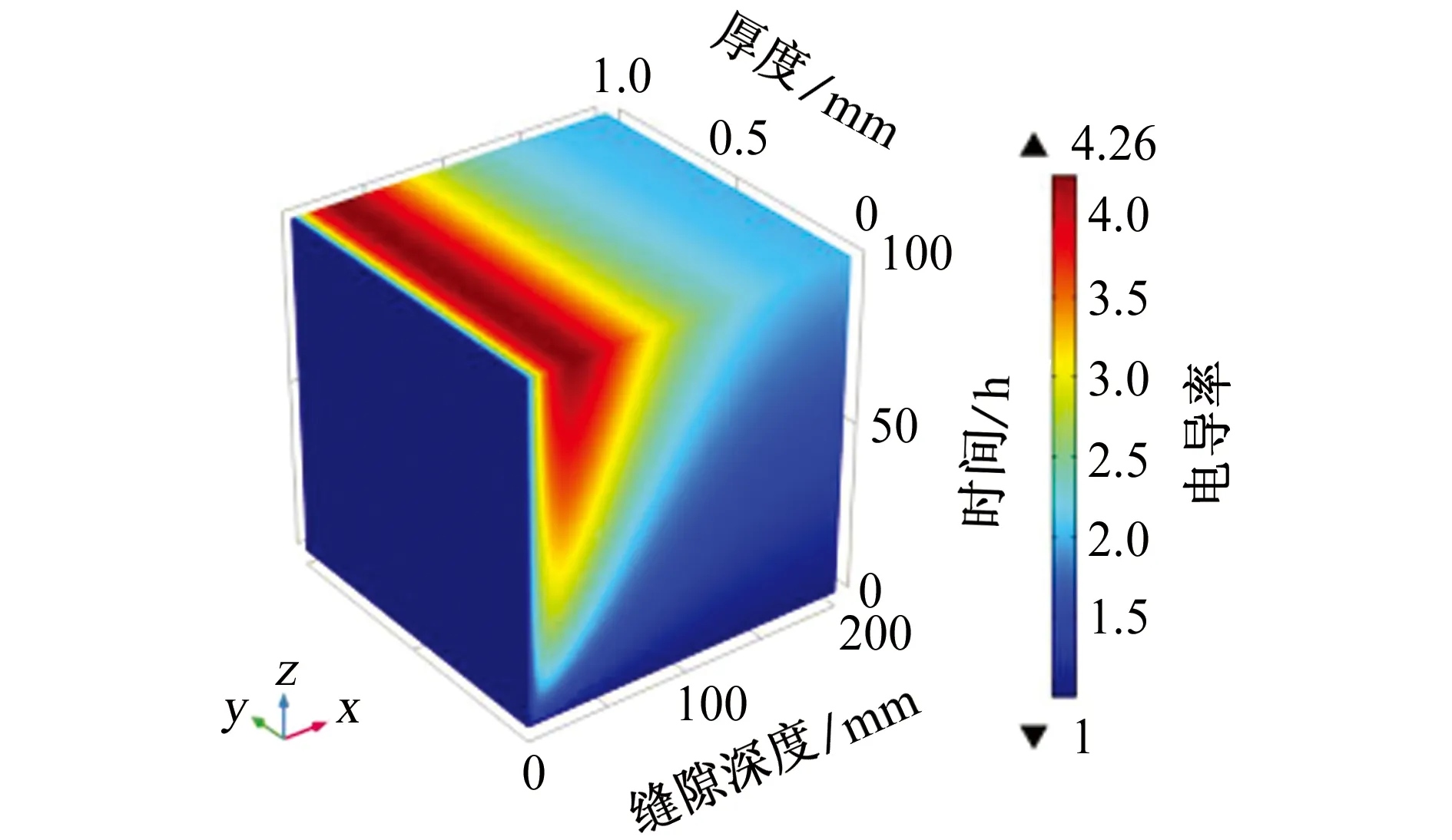
图10 溶液电导率与初始条件下溶液电导率的比值随缝隙深度和时间的变化Fig. 10 Variation of the ratio of solution conductivity to solution conductivity under initial condition with time and crevice depth

3 模拟计算结果与试验测量结果的比较

本工作参考了CHEN等[28]的试验研究，并与之进行比较，以说明模拟的准确性。试验采用X70管线钢，试验条件如下：以0.01 mol/L Na2SO4溶液作为土壤模拟溶液，pH为6.8，温度为室温(22 ℃)，缝隙深度为30 cm，厚度为0.9 mm，阴极保护电位为-1 000 mV。

如图11、图12和图13所示,通过数据对比，模拟结果和试验结果的平均误差为1.8%，这种偏差可能是模型的假设与实际情况仍存在差距所致。

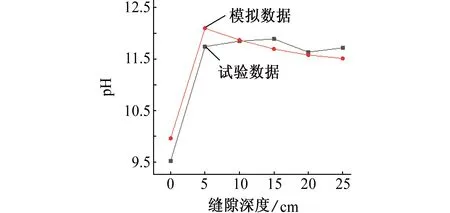
图11 72 h后模拟和试验所得的溶液pHFig. 11 Solution pH obtained by simulation and test after 72 h

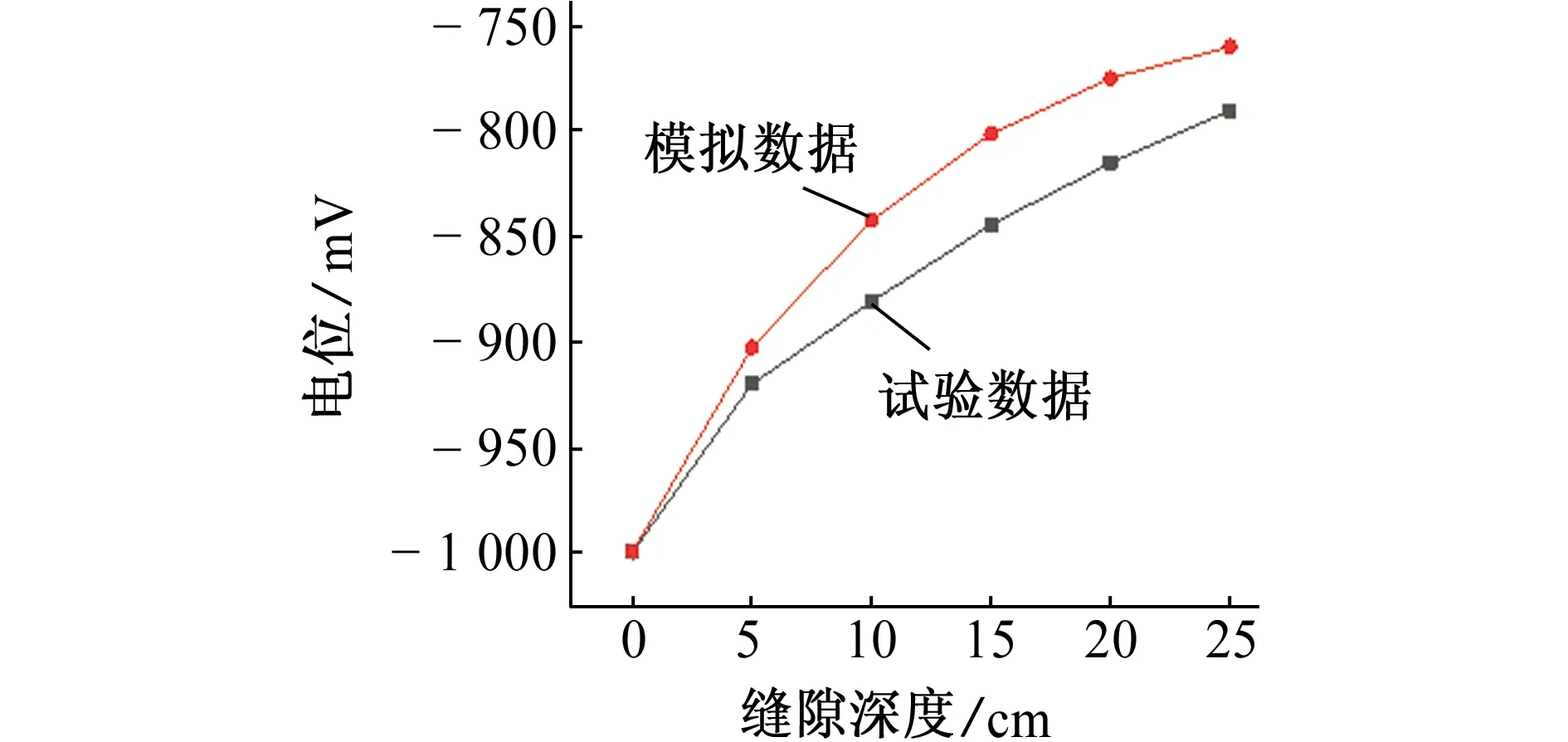
图12 72 h后模拟和试验所得的缝内电位Fig. 12 Potential in crevice obtained by simulation and test after 72 h

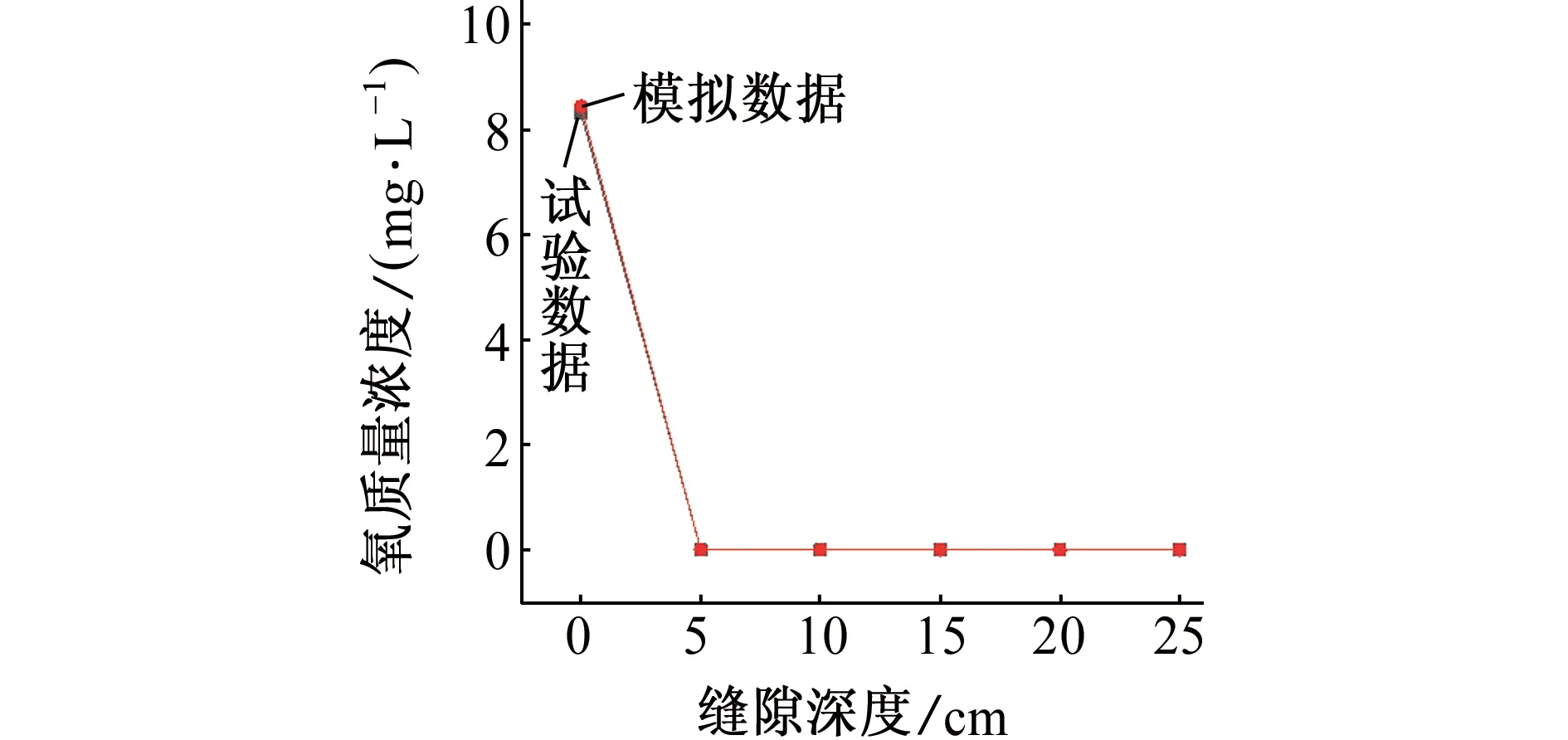
图13 72 h后模拟和试验所得溶液的氧质量浓度Fig. 13 Oxygen concentration of solution obtained by simulation and test after 72 h

4 结论

(1) 在结合前人的数学模型的基础上，开发了一个涂层下缝隙腐蚀的二维瞬态模型，将缝隙内化学物质的传质、还原反应和水的电离统一，利用有限差分法解决了方程的求解问题，模拟了阴极保护条件下，缝隙内化学和电化学反应随时间的演变，模拟结果与试验数据吻合度较好，两者平均误差为1.8%。

(2) 当缝内溶液含有溶解氧时，缝内发生氧的还原反应，氧气被消耗，在有阴极保护电流的情况下，在距缝口1.5 mm处溶液pH出现峰值，此处氧气被消耗殆尽，并且由于电中性和缝隙形状的特殊性，使得氧气无法进一步向缝内扩散。

(3) 本模型添加水的电离效果，当溶解氧被还原生成OH-的同时还有少部分OH-来自水的电离，这使模拟效果更佳贴合实际。在阴极保护条件下，缝内溶液的pH显著上升，在缝隙口处达到峰值，并随着时间的推移逐渐趋于稳定。而在高碱性环境中，缝隙内部的金属表面会形成钝化膜从而使其腐蚀速率降低，即使缝隙深处未受到阴极保护也能延缓腐蚀的发生。

(4) 缝隙中由于电迁移传质和浓度梯度影响下的扩散，使阳离子向内、阴离子向外运动，同时由于还原反应使缝口处OH-浓度迅速升高，导致溶液电导率随时间的延长而增加，并且随着深度的增加而减小。