雾计算中细粒度属性更新的外包计算访问控制方案

杜瑞忠，闫沛文，刘妍

（1.河北大学网络空间安全与计算机学院，河北 保定 071000；2.河北省高可信信息系统重点实验室，河北 保定 071000）

1 引言

云计算通过基础设施向用户提供服务，为应用提供弹性资源，但云计算提供的资源主要集中在远离用户的核心网络中，这导致用户和云之间交互信息时会产生时延。随着用户对低时延的需求越来越高，雾计算作为云计算的延伸被提出[1]。雾计算将云服务与靠近网络边缘的分布式资源相结合，使存储和数据处理等贴近网络边缘设备，可以提供外包计算、资源分配和缓存等多种服务[2-4]，有效缓解了云计算中存在的时延问题，在智能医疗、智慧城市等对低时延需求较高的领域被广泛应用[5-6]。

雾计算更贴近终端用户，数据中包含大量用户隐私信息，由于存在虚假节点恶意获取数据的情况，因此需要一种雾计算环境下高效的访问控制方案[7-8]。在雾计算中，边缘设备基于密文策略的属性加密（CP-ABE,ciphertext policy attribute based encryption）是实现细粒度访问控制的技术之一，数据所有者根据属性对数据进行加密，而不需要知道用户的确切身份，只有满足属性的用户才能对数据进行访问。CP-ABE 多采用门限秘密共享方案，需用多项式插值法来重建秘密，其解密阶段配对和求幂开销较大的计算，给雾计算中资源受限的边缘设备带来计算瓶颈。另外，雾计算中边缘设备的属性会频繁变化，为防止用户使用更新前属性密钥进行访问，需要建立有效即时属性撤销机制以提高其灵活性。

为了解决上述问题，本文提出了一种雾计算中细粒度属性更新的外包计算访问控制方案；结合雾计算的特点，建立了云-雾-用户分层的访问控制架构，用户通过雾节点与云进行交互；采用CP-ABE技术实现数据机密性和细粒度访问控制，并设计安全高效的外包加解密方案，将加密和解密中繁重的计算外包给雾节点，使用模加法技术构建访问控制树，避免了多项式插值法产生的计算开销，使加密、密钥生成和解密阶段的计算量更少，减少数据所有者和数据用户的计算负担；在雾节点建立组密钥二叉树生成属性组密钥，用户提交访问请求时对密文进行重加密，实现了属性的细粒度更新与即时撤销。通过雾节点对用户进行管理，减小了组密钥二叉树规模与更新私钥的用户数量，并在更新时将属性组内用户标记为未更新用户，避免了频繁更新私钥的冗余操作，提升了属性更新效率；对方案进行仿真实验对比，实验结果表明，用户加解密时间消耗较小且稳定，外包解密阶段耗时更少，属性更新时的效率更高。

本文主要的研究工作如下。

1) 建立更适用于雾计算的云-雾-用户分层的访问控制架构，雾节点对用户进行管理，用户必须通过雾节点与云进行交互。

2) 改进模加法机制构建访问控制树，降低计算开销，利用外包加解密思想和重加密机制设计了一种雾计算环境下细粒度属性更新的外包计算访问控制方案。

3) 进行安全性分析，基于决策双线性Diffie-Hellman 假设，证明了所提方案满足明文攻击安全。通过仿真实验分析与其他方案在各阶段运行时间进行对比，所提方案在满足安全性前提下，效率更高。

2 相关工作

2007 年，Bethencourt 等[9]首次提出CP-ABE 方案，之后其被广泛应用于云存储环境中数据的细粒度访问控制[10-11]，但由于加解密的计算开销随着访问结构中属性的数量线性增加，该方案效率较低且不适用于资源受限的边缘设备。Ibraimi 等[12]提出了一种高效的CP-ABE 算法，该算法使用模加法一致同意控制方案（UCCMA,unanimous consent control by modular addition）建立访问控制树，避免多项式插值法的计算开销。为了进一步提高效率并减小用户负担，将加解密阶段的复杂计算进行外包[13-14]。Jin 等[15]以文献[12]为基础，设计了安全轻量级的访问控制方案用于移动云计算，引入加密服务提供商（ESP,encryption service provider）和解密服务提供商（DSP,decryption service provider）降低加解密过程中的计算开销，在实现系统高效性的同时，将移动设备大部分计算外包给ESP 和DSP，使移动设备可以有效地对存储在云端的数据进行访问和管理。Green 等[16]改进了ABE（attribute based encryption）外包系统中的密钥生成算法，使用盲密钥技术生成转换密钥并发送给第三方代理，将满足访问策略的密文转换为简单密文，使明文恢复所需开销较小。为解决外包计算的正确性问题，Mao等[17]和Kumar等[18]提出了基于属性的可验证外包解密的访问控制方案，外包计算后验证了数据的正确性，用户解密密文时只需要进行恒定数量的计算。外包计算的访问控制方案得到了广泛应用，Kibiwott 等[19]提出了基于云的电子健康大数据系统访问控制方案，通过cloudlet 服务器进行外包计算，实现了机密性和数据完整性。但以上外包计算方案没有考虑属性撤销问题，在动态性较强的雾计算中并不适用。

在CP-ABE 方案中，为防止用户使用过期的属性密钥，必须使用密钥撤销机制。Al-dahhan 等[20]通过管理联合属性集存储数据，提供策略更新和密钥失效2 种技术来消除共谋攻击，并解决密钥撤销问题，但密钥维护代价和计算复杂度高。Zhang 等[21]提出了一种雾环境下外包加密和属性更新方案，在属性更新时，所有拥有该属性的用户必须对属性密钥进行更新，对未撤销属性进行大量计算，这会大大降低属性更新的效率。为了避免撤销属性时密钥的大量更新，Chen 等[22]在方案中引入衰落函数，使属性密钥可以随时间进行动态更新，需要为每个属性设置生存周期，但选取合适的生存周期是一个难题，且衰落函数存在产生冲突的情况。Hur 等[23]提出了一种建立二叉树对密文双重加密的方法，庞大的设备数量会导致二叉树的维护开销较大。Liu等[24]将用户身份信息分配给叶子节点信息以跟踪恶意用户，并通过将恶意用户添加到吊销列表和更新密文，实现对恶意用户的撤销操作。张凯等[25]提出了高效撤销的多机构访问控制方案，将撤销列表嵌入密文对用户的整体属性进行撤销，但无法对部分属性进行撤销操作，存在撤销粒度较粗的问题。以上方案虽然解决了属性撤销问题，但目前属性密钥撤销仍然给系统带来较大的开销。

综上所述，传统的访问控制方案效率较低，并缺乏高效的属性撤销方法。为此，本文提出了雾计算中细粒度属性更新的外包计算访问控制方案，在保障安全的前提下，降低用户开销，提升属性更新效率。

3 预备知识

3.1 双线性映射

G,GT是2 个阶为P的循环群，g是G的生成元，双线性映射e:G0×G0→GT满足以下性质。

1) 双线性：对任意u,v∈G0和a,b∈Zp，都有e(u a,vb)=e(u,v)ab。

2) 非退化性：存在u,v∈G0使e(ua,vb) ≠ 1。

3) 可计算性：对于任意的u，v，存在一个有效的算法计算e(u,v) 。

3.2 访问控制树

令根节点为r的访问控制树T描述访问控制策略，该策略指定了在解密密文时需要的属性组合。T中的每一个内部节点都是逻辑运算符，例如AND、OR。每个叶子节点都表示一种属性。属性可以是定义、分类或注释用户的任何描述性字符串。根据秘密共享的思想，访问树的每个节点表示一个秘密。在加密阶段需要自顶向下递归地为每一个节点分配一个秘密。而在解密阶段，需要自底向上回复根节点的秘密。

3.3 秘密分享

在秘密分享方案中，发放者将一个秘密S分割成t份，需要所有的分割部分才可以重新构造出S。为了共享秘密S（0≤S≤p-1），发放者生成t-1个随机数Si，即1≤Si≤p-1，1≤i≤t-1，同时。秘密S通过进行恢复，将Si分享给Pi个参与方，1≤i≤t。对每一个参与者Pi，得到的是0～p-1 的随机数，因此，除了发放者之外没有任何一方知道关于秘密S的任何信息。

3.4 决策双线性

决策双线性Diffie-Hellman（DBDH,decision bilinear Diffie-Hellman）问题的定义如下。挑战者根据安全参数选择一组阶为素数p的G0。让g作为生成元，选取随机数a,b,s∈Zp。如果挑战者给予对手(g,g a,g b,gs)，对于对手来说，将很难区分有效的元组e(g,g)abs∈GT与随机元素R∈GT。

一个概率性多项式时间算法Q能够以优势ε求解DBDH 问题，当且仅当满足

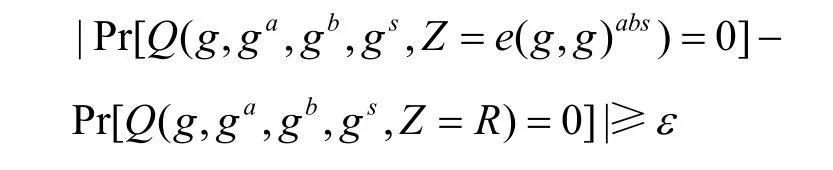
如果概率多项式在解决DBDH 问题上的优势可以忽略不计，则DBDH 假设成立。

4 系统模型

4.1 整体框架

本文为解决雾计算中用户加解密开销大、属性更新效率低的问题，设计了云-雾-用户分层的系统模型，主要由5 类实体组成，系统结构如图1所示。

云服务提供商（CSP,cloud service provider）。CSP 提供数据存储等方面的服务，在本文方案中假设CSP 可信。

雾节点。雾节点提供计算、存储等服务，负责对密文进行外包加解密计算，生成组密钥对密文进行重加密，并在未更新用户提交访问请求时，更新其私钥。

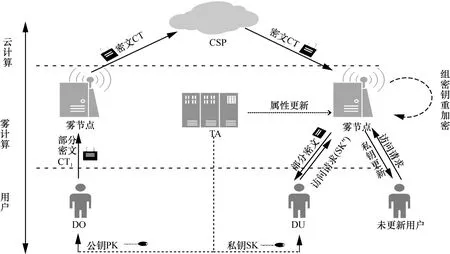
图1 系统结构

数据所有者（DO,data owner）。DO 是有文件要上传到云端存储的用户，为文件定义访问结构，然后生成部分密文发送到雾节点。

数据用户（DU,data user）。DU 是访问存储在CSP 中的文件的用户，当数据用户的属性集满足嵌入给定密文中的访问结构时，可以从密文中解密文件。若用户被标记为未更新用户，在请求访问时需要先更新私钥。

可信权威机构（TA,trusted authority）。TA 是完全受信任的一方，遵循协议规范执行分配任务，然后输出正确的结果，主要负责处理用户注册，为每个系统用户生成系统参数和密钥SK，向雾节点发送属性更新信息。

4.2 算法定义

本文系统由系统初始化（Setup）、私钥生成（KeyGen）、数据加密（Encrypt）、组密钥生成（GKeyGen）、密文重加密（reEncrypt）、私钥更新（upGKeyGen）、密文解密（Decrypt）几个算法构成。

1) 系统初始化Setup(1k,L)→(PK,MSK)。初始化阶段输入安全参数k和属性域L={a1,a2,…,am}，进行运算获得系统的公钥PK 和主密钥MSK。

2) 私钥生成KeyGen(MSK,S)→SK。私钥生成算法通过输入主密钥MSK，以及私钥所包含的属性集合S，计算得到私钥SK 并发送给用户。

3) 数据加密Encrypt。为了获得较高的加密效率，DO 首先使用随机密钥ck 对指定文件进行加密，然后使用对称加密算法对ck 进行加密，该算法包含以下2 个子算法：DO 在本地运行DO.Encrypt，雾节点运行外包加密算法Fog.Encrypt。

DO.Encrypt(PK,ck,A)→C1T，算法输入PK、ck 和访问结构A，然后输出部分密文C1T，最后DO将C1T 发送给雾节点。

Fog.Encrypt(PK,CT1)→CT，该算法输入PK 和CT1，然后输出密文CT 并发送给CSP。

4) 组密钥生成GKeyGen(a1,a2,…,am)。该算法输入属性域L={a1,a2,…,am}给雾节点，雾节点为用户生成二叉树τ并推算出组密钥Ej（1 ≤j≤m）。

5) 密文重加密reEncrypt(Ej,CT) →CT′。雾节点收到数据用户访问请求后，从CSP 获取密文CT，利用生成的组密钥Ej（1 ≤j≤m）与密文CT 进行运算，得到重加密密文CT′。

6) 私钥的更新upGKeyGen(iE,SK) SK′→。用户通过计算得到组密钥Ej，与SK 中对应的属性私钥进行更新运算，得到新私钥SK′。

7) 密文解密Decrypt。雾节点接受用户发来的部分密钥SK′，与重加密之后的'CT 进行计算得到T，并发送给用户。如果用户的密钥满足访问结构A，则运行以下算法得到ck，该算法包括2 个子算法：雾节点运行外包解密算法Fog.Decrypt，用户执行本地子算法User.Decrypt。

Fog.Decrypt(PK,CT′,SK′)→T。输入PK、CT′和SK′，通过计算输出结果T，并将其发送给DO。

User.Decrypt(T,SK)→ck。使用T和SK 进行计算，生成密钥ck。

因此，使用 ck 通过对称解密算法将得到文件。

5 方案描述

本节描述了雾计算中细粒度属性更新的外包计算访问控制方案的具体结构。雾计算应用对低时延有较高需求，因此降低用户计算复杂度和提高属性更新效率成为用户的重要需求。首先，本节提出一种安全外包加解密方法，以减少用户在访问控制过程中的计算负担。外包方法主要是将加密和解密阶段所有访问结构和属性相关的操作外包给雾节点，留给数据所有者和数据用户执行少量操作。然后，利用重加密机制在雾节点和用户之间构建一个组密钥二叉树τ，随机生成树中的节点密钥，并生成组密钥，当用户的属性要增加或者撤销时，仅需改变属性的组密钥即可实现属性的细粒度更新。

5.1 具体方案

假设系统中拥有m个属性并表示为L={a1,a2,…,am}，将用户所属雾节点设置为一种属性。e:G0×G0→GT为双线性映射，G0为素数阶p以g为生成元的双线性群。哈希函数H:{0，1}*→G0，将任意属性映射到G0的一个随机元素上，具体细节如下。

阶段1系统初始化Setup

Setup(1k,L)→(PK,MSK)。系统定义阶为p、以g为生成元的双线性映射群e:G0×G0→GT，随机选取参数α∈Zp，对任意a j∈L选取一个随机数vj，计算PKj=gvj，设置雾节点属性值为Afg∈Zp，最后得到公钥与主密钥。

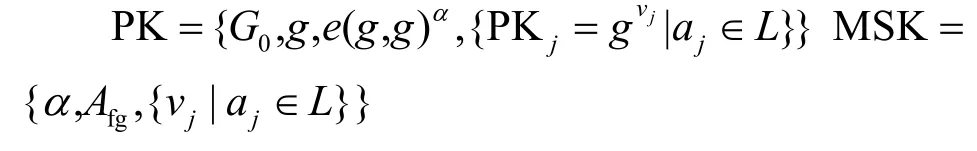
阶段2私钥生成KeyGen

KeyGen(MSK,S)→SK。该算法首先随机选择r=Z p，r是分配给每个系统用户的唯一密钥；然后，选取随机数y∈Zp，将雾节点属性标记为Dfg，计算私钥。

阶段3数据加密Encrypt

在文件M上传到CSP 之前需要进行的步骤如下。

1) DO.Encrypt(PK,ck,A)→C1T。DO 定义一个访问结构A，并随机选取密钥ck，用对称加密算法对M进行加密，加密后的密文表示为Eck(M)。DO随机选择S'∈Zp，计算=cke(g,g)βs'。输出密文CT1={A,Eck(M)，=ck（e g,g）βs′C=gs′}。用户DO 发送CT1给雾节点。

2) Fog.Encrypt(PK,CT1)→CT。雾节点根据收到的访问结构A建立访问控制树T，如图2 所示，为T的根节点赋值为S，随机选择Sfg∈Zp将其作为根节点的右子树，其他子节点标记为未赋值，对于每个未赋值的非叶子节点递归地执行以下操作。

如果运算符是AND 且它的子节点未赋值，使用模加法方案为每个子节点赋值，对于除了最后一个子节点之外的每一个节点赋值为随机数Si（1 ≤Si≤p-1），将最后一个子节点赋值为。

如果运算符是OR，为每一个子节点赋值S。T树中叶子节点的值用来生成密文。为每一个叶子节点属性a∈T，计算属性密钥C=gvjsi，i为访问树的索引属性，对于给定的访问结构，索引值被唯一地以排序的方式分配给节点。

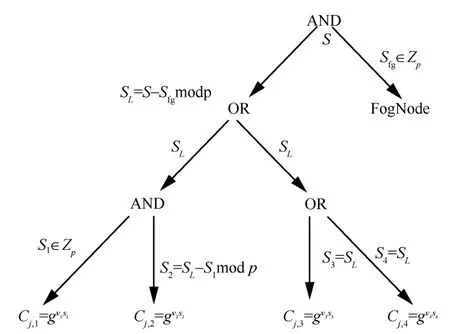
图2 访问控制树

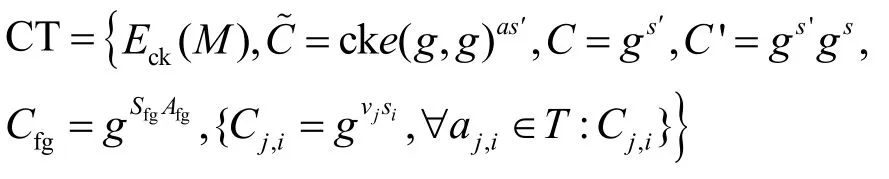
最后通过计算得到

阶段4组密钥生成GKeyGen

组密钥二叉树τ的构成原理如下。雾节点根据管理用户构建二叉树τ，如图3 所示，将所有用户分配到叶子节点，并为τ中的每一个节点生成一个节点密钥un,m∈Zp，用户叶子节点到根节点通过的节点称为路径节点，用户存储路径节点的节点密钥。雾节点为属性定义一个公开参数γj∈Zp，根据属性所对应的用户组，找到包含用户的最大覆盖子树，建立组密钥Ej={V1,1,V2，1,…,Vn,m||γj}，通过门限法将Ej设置为(S,2)秘密共享，推算出Ej。假设属性ωj的用户组为{u1,u2,u3,u4,u7,u8}，在组密钥二叉树中的最大覆盖节点为{V2,1,V3,4}，则属性ωj的组密钥为Ej={V2,1,V3，4||γj}。

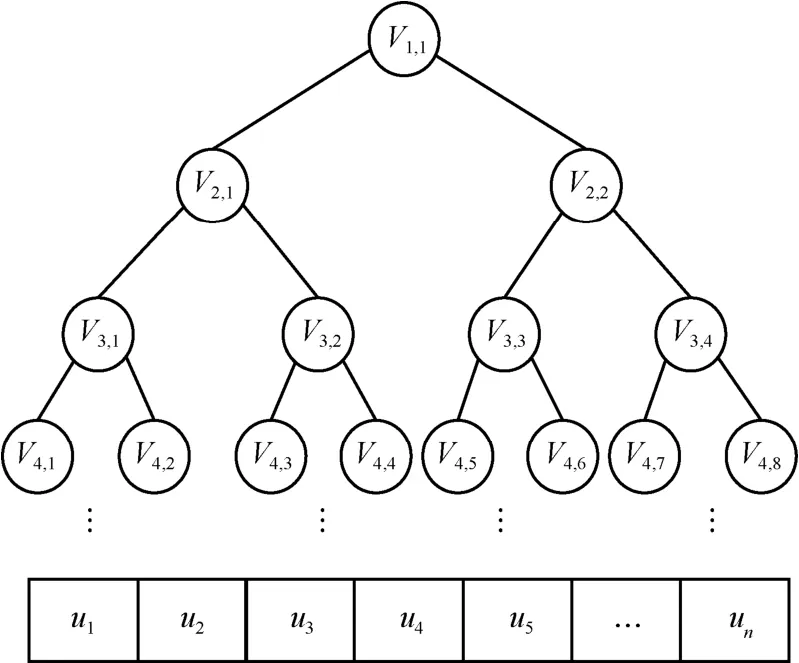
图3 属性组密钥二叉树

阶段5密文重加密reEncrypt

当用户向雾节点请求访问数据后，雾节点从CSP 获取密文CT，然后通过组密钥Ej对CT 进行重加密，计算得到

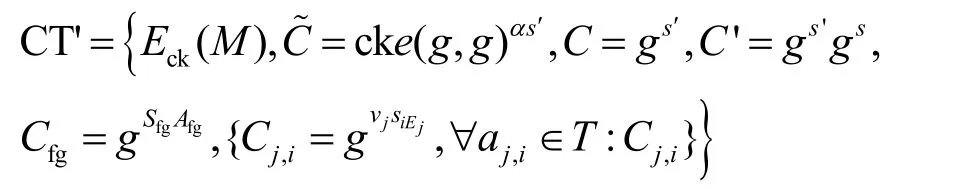
阶段6密钥更新upGKeyGen

雾节点接收到DO 的访问请求之后，如果数据用户被标记为未更新用户。雾节点将其需要更新属性路径节点所在二叉树层数发送给用户。门限方案中Ei设置为(S,2)秘密共享，只要知道两部分就可以计算出组密钥Ei，由于γi是公开的，因此只要属性覆盖用户组内包含该用户，便能够计算出Ei，DO 利用E进行计算，=，则更新之后的私钥为

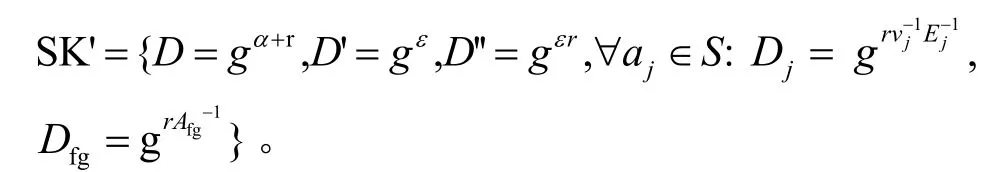
阶段7密文解密Decrypt

如果用户拥有的属性满足访问结构A，则运行下面的解密算法解密CT，获得内容密钥ck，用户可以使用ck 解密Eck(M) 并获得明文M，由于密文和密钥进行双线性配对操作需要大量的计算开销，因此解密的计算开销非常大，为了减少用户的计算开销，将这些操作外包给雾节点。该解密算法分为外包解密算法Fog.decrypt 和User.Decrypt。

1) Fog.Decrypt(PK,CT′,SK′)→T。雾节点从用户接受部分密钥SK''={D'=g y,D''=gyr,∀aj∈S:D=grv-j1E-j1,D=grAfg-1}对私钥中的D与重加密后的CT′中的Cj,i进行如下运算

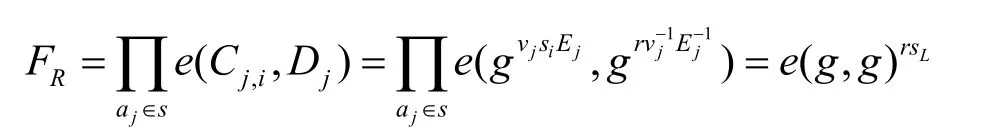
雾节点接着计算

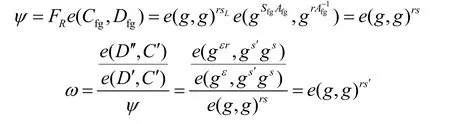
将得到的T={Eck(M),C～=cke(g,g)αs′,C=g s′,ω}发送给用户。

2) User.Decrypt(T,SK')→ck。用户收到雾节点发送的T，与私钥SK'计算得到ck。

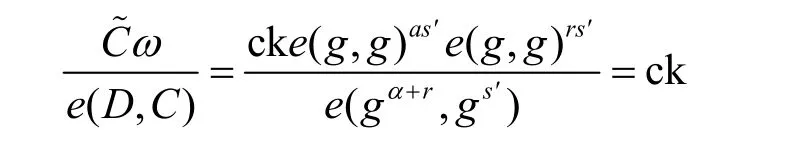
因此，使用ck 通过对称解密算法将得到M。

5.2 属性更新

1) 属性添加与撤销

当用户属性进行添加或撤销时，雾节点根据更新后用户叶子节点重新寻找其最大子树的根节点，运行GKeyGen 算法完成组密钥的更新。用户添加或撤销新的属性jω时，TA 将属性的更新信息发送给雾节点，雾节点根据更新后属性jω包含的用户组，寻找能覆盖所有用户的最大子树节点，根据组密钥的构成方法计算得到新Ej′。将其他拥有属性jω的用户标记为未更新用户，当未更新用户向雾节点发送访问请求时，进行私钥更新，避免在属性频繁更新时，给用户带来冗余操作。属性jω的组密钥更新不会影响其他雾节点域内属性的组密钥，仅需要该雾节点域内持有该属性的用户更新私钥，减小了更新所带来的操作开销。

2) 用户整体变更

对用户的变更分为用户加入与撤销，可以看作向新用户分配属性和将老用户的所有属性进行撤销。因此，用户的整体变更可以归纳为对属性更新。

①当用户节点加入系统时，将用户分配到空叶子节点，为用户生成组密钥，并对用户私钥进行更新。

② 当用户节点离开系统时，则修改用户从叶子节点到根节点的所有密钥链。首先雾节点生成随机数Vtmp∈Zp，Vtmp与密钥链节点进行XOR 操作生成新的节点密钥；完成更新的节点将其节点密钥通过广播加密的方式发送给其子树的叶子节点。

6 安全性分析

在所提雾计算中细粒度属性更新和外包计算访问控制方案中选择明文攻击安全模型，基于DBDH问题进行安全性分析。设G,GT为2个阶为P、生成元为g的双线性群，双线性映射e:G0×G0→GT。模型生成（g,g a,g b,g s,Z)，其中a,b,s,θ∈，设置参数ϑ∈{0,1}，一个随机元素R∈GT，当参数ϑ=0时，Z=e(g,g)abs；否则Z=R。

定理1如果故手A 能够在一个概率多项式时间内以不可忽略的优势ε＞0 求解，那么算法φ能够区分一个DBDH 元组和一个随机元组，并且优势为ε/2。

证明敌手A 和挑战者B 执行操作如下。

初始化敌手A 定义访问控制树T*，并发送给挑战者B。

系统设置挑战者B 对系统进行初始化，B 选择一个随机数χ′∈Zp，计算α=χ′+ab。设置u=e(g,g)α=e(g,g)χ'e(g,g)ab。对每一个属性a j∈L，B 选择随机数sj，如果a j∈T*，则v j=；如果a j∉T*，则v j=sj。最后B 将公钥PK={G0,g,u,{PKj|a j∈L}}发送给敌手A。

挑战阶段敌手A 向挑战者B 发送长度相同的两段信息m0和m1，B 选择一个值S′∈Zp，随机选取参数ϑ∈{0,1}，通过执行Encrypt 和reEncrypt 算法对信息mϑ进行加密。B 构造密文CT1中的和C。

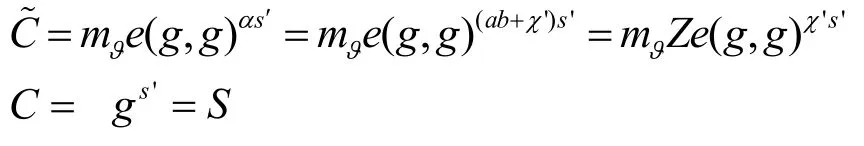
然后，将CT1发送到雾节点，雾节点设S为访问控制树T*的根节点的值，根据访问控制树T*的构造方法对每个叶子节点属性aj,i∈T*，计算C=gvjsi，gs，则C'=g s'gs=Sgs，C=gAfgSfg得j,ifg到密文CT，雾节点运行重加密算法将CT 更新为

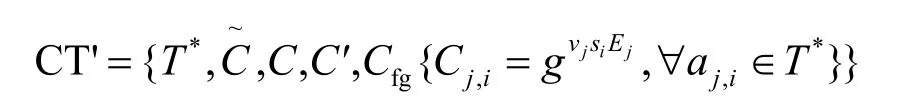
挑战者B 将密文返还给A。

阶段2同阶段1，敌手A 可以继续向挑战者B 进行询问。

猜测游戏中如果ϑ'=ϑ，挑战者B 输出0，表明Z=e(g,g)abs；否则，B 输出1，表明Z=R。当Z=e(g,g)abs时，A 获得有效的密文，则A 的优势为

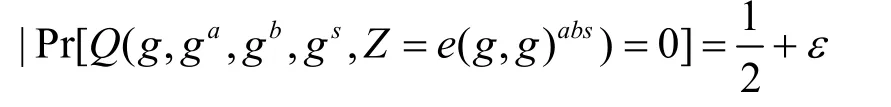
当Z=R时，A 无法获得任何明文信息，即

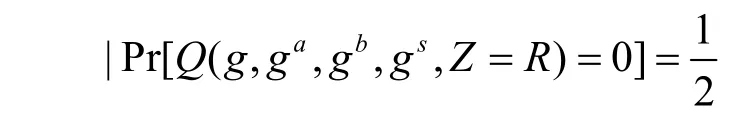
因此，φ的优势为

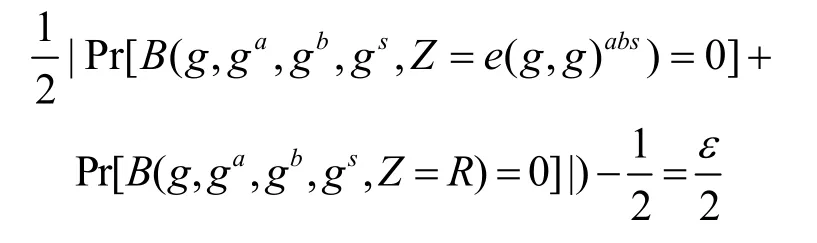
在以上挑战过程中，假设DBDH 成立，如果没有敌手在多项式时间内完成，则本文方案是满足选择明文攻击安全的，且该方案具有前后向安全性、抗共谋安全性。

1) 在本文方案属性更新机制中，当添加或者撤销用户属性时，雾节点运行GKeyGen 算法更新组密钥得到Ej'，再运行upGKeyGen 算法对用户私钥进行更新得到SK'，因为在门限方案中将E′j设置为(S,2)秘密分享，在该属性用户组内的用户可以利用Lagrange 插值得出组密钥，所以已撤销属性的用户无法推出；同理，添加属性的用户也无法通过，在雾节点进行外包解密计算FR时，。因为组密钥无法匹配问题，无法计算得到 (,)rsL e g g，便无法对密文进行解密，所以本文方案满足前向后向安全性。

2)DO设置访问结构A对文件进行加密，只有DU 的属性S∈A时才能解密cke(g,g)βs'。假设多个未满足访问结构的用户相互勾结交换密钥，组成了满足访问结构中的属性集。根据密钥生成KeyGen算法，不同用户的身份标识r都是随机数，则产生不同的私钥D j=grv-j1，若互相勾结的用户身份表示分别为r1,r2，通过计算得到FR=e(g,g)r1r2sL，A=e(g,g)r1r2s，便无法推出e(g,g)rs'，所以仍然无法对密文进行解密。因此，方案具有抗串谋攻击性。

证毕。

7 性能分析

在性能分析中，对本文方案在理论上和实验上进行分析，证明其可行性。将本文方案与其他方案进行功能比较，结果如表1 所示。

表1 功能比较

7.1 理论分析

在理论分析中，将本文方案与其他方案在性能和计算开销方面进行了比较。为了更好地理解分析，表2 总结了所使用的符号，表3 针对方案中加解密开销与属性更新开销进行了比较。

从表3 可以看出，文献[12,24]方案没有进行加解密的外包，用户的计算开销是巨大的，会随着访问结构的复杂化而加大计算量。但使用了模加一致性构建访问控制树的文献[12]方案在用户加密与解密时，计算开销小于使用了线性秘密分享方案（LSSS,linear secret sharing scheme）访问结构的文献[24]方案。其他方案对加解密计算进行了外包，因此用户的计算量是恒定的，与属性以及访问控制结构无关。文献[18]方案在用户解密时直接将对称密钥通过第三方审计平台发送给用户，使用户只需要进行一次对称解密就可以解密密文，虽然解密效率更高，但存在安全隐患，对称密钥如果泄露，数据将会被获取。在用户外包解密方案中，本文方案使用了模加法技术构建访问控制树，减小雾节点外包解密的开销，在外包解密中本文方案是最优的。在属性撤销方面，文献[21]方案为了实现用户属性的即时撤销，在属性发生撤销时，需要对该用户以及其他持有该属性的用户更新私钥，当用户数量庞大且属性需要频繁更新时，计算开销是巨大的。文献[24]方案为了实现撤销机制，将撤销方法嵌入加解密中，使用户所持有属性在加解密时都要进行是否撤销的判断操作。本文方案通过雾节点对密文进行重加密便可以实现对属性的即时撤销。综上所述，本文方案为实现外包加解密和属性更新，在保证安全性的前提下，计算开销与其他方案相比较低。

表2 性能分析中使用的符号

7.2 实验分析

通过仿真实验将本文方案与文献[18,21,24]方案在外包加密、外包解密与属性更新等方面进行比较分析。本文在charm-crypto 框架内进行仿真实验，使用英特尔i5-4200U 2.3 GHz 处理器，8 GB 内存，搭建环境为Ubuntu14.04 64 位系统与Python2.7。实验中所有结果均为10 次结果的平均值。

用户加解密时间的比较如图4 所示。从图4可以看出，没有涉及外包加解密的文献[24]方案随着属性数量的增多，用户加密时间线性增长；本文方案与其他外包加解密方案在用户进行加解密操作时，将复杂计算外包出去计算，用户所消耗的时间是基本恒定的，因此不会随着属性数量的增加而增长。在图4(a)中，在用户加密的效率方面使用了外包加密的方案所消耗时间较相近，可以看到本文方案是较优的。在图4(b)中，文献[18]方案在设计外包解密时，由第三方审计直接将对称加密密钥发送给用户，用户在解密时只需要进行一次对称解密，所以用户解密时间要低于本文方案，但是直接将对称加密的密钥进行传输，会带来一些安全性问题。在安全性的前提下，本文方案用户解密效率较高。

表3 计算开销比较

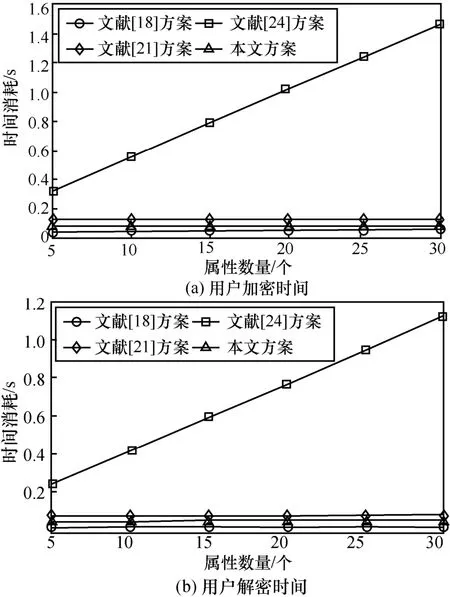
图4 用户加解密时间的比较

外包加解密时间的比较如图5 所示。从图5 可以看出，外包加密时方案之间的差异较小，时间消耗随着属性数量的增加线性增长，所以访问控制策略越复杂加密时间也会越大。外包解密中，因为本文方案使用UCCMA 技术建立访问控制树，避免了多项式插值法产生的巨大计算开销，计算时间上低于其他方案，随着属性数量的不断增多，这种优势将逐渐扩大。

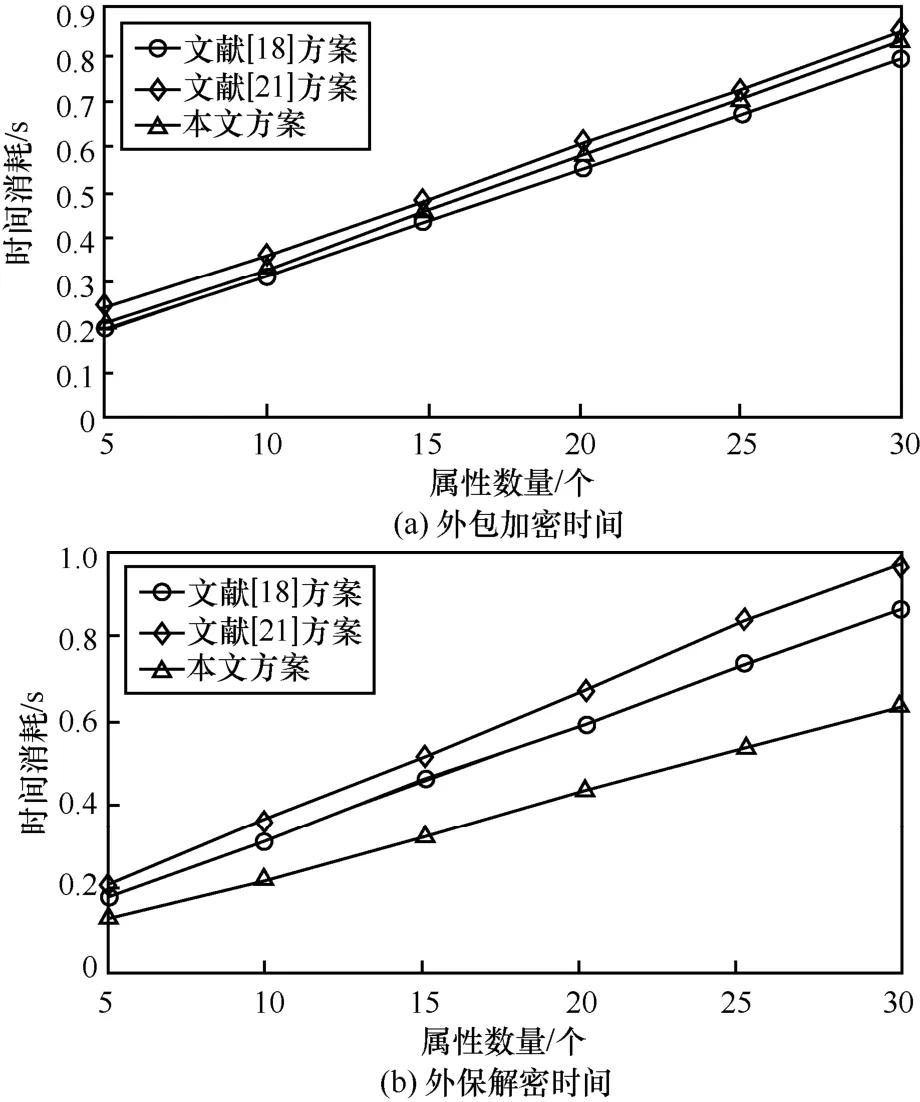
图5 外包加解密时间的比较

属性更新时间的比较如图6 所示。仿真实验中，假设所有的用户都拥有要更新的属性，图6(a)中设定用户数量为30，图6(b)中设定更新次数为2 次。文献[24]方案为了实现对属性的撤销，将属性撤销嵌入加解密过程中，导致用户在进行加解密操作时所持有属性都需要进行计算，使用户在加解密时开销太大，所以在此不做比较。文献[21]方案在属性更新时，为了实现属性的即时更新，需要立即对所有持有该属性的用户进行私钥的更新，随着用户数量的增多，以及属性更新次数的增加，该方案在属性更新时的开销会越来越大。本文方案实现对属性的即时更新，只需要改变属性对应组密钥并对密文进行重加密操作，因为用户由不同雾节点管理，更新用户私钥时只需要对当前雾节点内用户私钥进行更新，当短时间内属性频繁更新时，未与雾节点进行交互的用户只需要更新一次私钥即可。图6(a)中用户数量恒定，随着更新次数的增加本文方案时间消耗趋于稳定，文献[21]方案呈线性增加趋势。图6(b)中更新次数为2 次时，随着用户数量的增加，本文方案与文献[21]方案均呈线性增加趋势，但本文方案增加速率相对较慢。所以本文方案在属性更新方面效率较高。

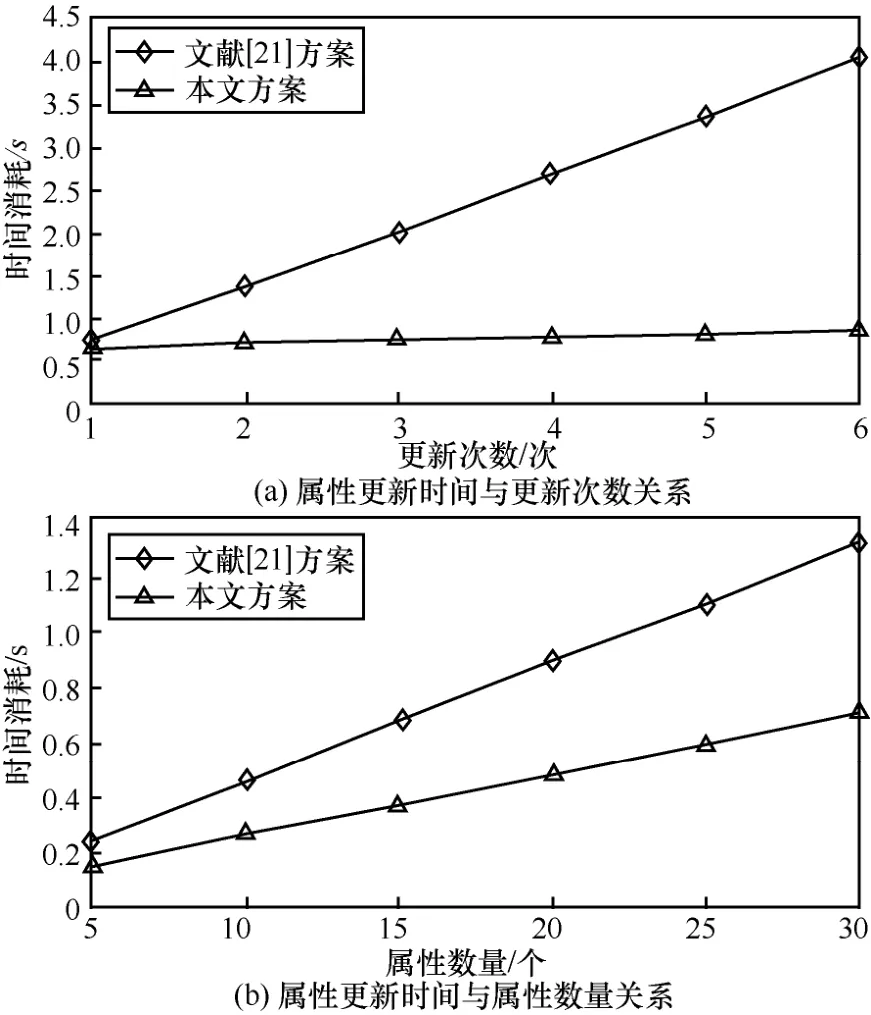
图6 属性更新时间的比较

8 结束语

本文提出了一种雾计算中细粒度属性更新的外包计算访问控制方案，将加解密的复杂运算外包给雾节点，降低了用户的计算开销，并通过重加密的方法实现了属性的细粒度更新，能够根据需求完成对属性的添加与撤销。在安全性的前提下保证了其高效率，通过决策双线性Diffie-Hellman 假设分析了安全性，通过仿真实验计算了在用户加解密、外包加解密和属性更新时的计算开销，得出本文方案中的用户终端设备开销较小，属性更新时效率较高，更适用于雾计算。

本文还存在一些不足，方案中通过雾节点对用户进行管理，没有涉及雾节点域的划分，并且随着万物互联的发展，海量边缘设备的增多，存在虚假节点或用户骗取数据的情况。在用户跨域访问时实现跨域的认证至关重要，因此雾环境下用户如何跨域认证实现动态高效且安全的访问控制是下一步需要研究的内容。