轻量级密码算法TWINE 的唯密文故障分析
2021-04-09李玮汪梦林谷大武李嘉耀蔡天培徐光伟
李玮,汪梦林,谷大武,李嘉耀,蔡天培,徐光伟
(1.东华大学计算机科学与技术学院,上海 201620;2.上海交通大学计算机科学与工程系,上海 200204;3.上海交通大学上海市可扩展计算与系统重点实验室,上海 200204;4.上海交通大学上海市信息安全综合管理技术研究重点实验室,上海 200093)
1 引言
物联网是一种物与物进行信息交换和通信的网络。它通过智能设备和机器感知收集有关数据,提取数据中有用的信息并提供方便快捷的服务。物联网的发展促进了大量新兴领域的发展,例如智能家居、智慧医疗、精准农业、智慧交通等[1-4]。由于物联网中的智能设备及传感器的处理、存储资源有限,在收集、传送和处理网络中的大量数据时,传统的密码算法较难有效地保证信息的机密性、完整性和认证性,因此,运行效率高、吞吐量小和安全性高的轻量级密码算法适用于物联网中的安全数据处理[5-7]。
TWINE 是2012 年在SAC(selected areas in cryptography)会议上提出的一种具有广义Feistel结构的轻量级分组密码,旨在保护资源受限的终端设备的数据安全[8]。现有的TWINE 的传统密码分析包括不可能差分故障分析、饱和分析、Biclique分析、零相关线性分析、中间相遇分析等[8-11]。但是,在物联网环境中,攻击者可以通过激光照射、异常时钟、涡流磁场等方式注入故障,干扰密码的加密过程,这些故障会使中间状态的计算产生偏差,通过分析或者统计错误中间状态即可恢复密钥并破译密码,这种攻击方法称为故障分析(FA,fault analysis)。
故障分析是在1997 年由Boneh 等[12]提出的一种密码分析方法,它通过在密码设备运行过程中注入随机的故障,干扰正常运行过程,从而恢复出密钥并破译密码。后来,故障分析衍生出差分故障分析(DFA,differential fault analysis)、不可能差分故障分析(IDFA,impossible differential fault analysis)、中间相遇故障分析(MFA,meet-in-the-middle fault analysis)、统计故障分析(SFA,statistical fault analysis)和唯密文故障分析(CFA,ciphertext-only fault analysis)等[13-17]。这些分析方法是轻量级安全密码实现的重要实际威胁之一。
根据攻击能力的强弱,密码分析方法的攻击假设可以分为选择明文攻击(CPA,chosen-plaintext attack)、已知明文攻击(KPA,known-plaintext attack)和唯密文攻击(COA,ciphertext-only attack)等。针对TWINE 的传统密码分析、现有故障分析的攻击假设主要集中在已知明文攻击和选择明文攻击,即攻击者需要获取当前密钥下的一些明文密文对,或特定明文对应的密文,这对攻击者的能力要求较强。在资源受限的物联网环境中,唯密文攻击对攻击者的能力要求最弱,攻击者仅需获取密文,因此容易在实际中应用,并可以有效地检测密码算法的实现安全性。
基于唯密文攻击的攻击假设,唯密文故障分析通过密码设备运行过程中注入随机故障,利用错误密文推导出的中间状态,分析相关的统计信息,在仅获得错误密文的情况下即可破译密码。TWINE作为广义Feistel 结构的典型密码之一,目前国内外都没有针对该密码的唯密文故障分析的相关研究,本文提出了针对TWINE 的新型唯密文故障分析方法,设计并实现了3 种新型区分器,从而降低了攻击代价,有效地提高了攻击效率。该方法的提出对于分析轻量级密码算法的安全性具有参考价值,同时对于增强物联网中信息的保护具有现实意义。
2 相关工作
密码分析是评测密码算法安全性的重要手段,国内外学者使用多种密码分析技术对TWINE 进行了安全性分析。在传统密码分析方面,TWINE 的设计者分别利用不可能差分分析、饱和分析等对TWINE 的安全性进行评估[8]。2012 年,Çoban 等[9]使用Biclique 构造和中间相遇分析搜索密钥,对TWINE 进行了Biclique 分析。2014 年,Wang 等[10]使用改进的零相关线性分析检验TWINE 的安全性,利用密钥编排方法的弱点并使用部分压缩技术降低了零相关线性分析的计算复杂度。2016 年,Tolba 等[11]利用广义中间相遇攻击,通过允许将密钥划分为3 个子集来消除中间相遇攻击的限制,实现对TWINE 的全密码攻击。以上攻击的假设均为选择明文攻击或者已知明文攻击。
在故障分析方面,2013 年,Yoshikawa 等[18]提出了差分故障分析,利用与同一明文相对应的一个正确密文和不同轮注入故障产生的错误密文,恢复了TWINE 的80 bit 主密钥。2015 年,Li 等[19]对TWINE 进行了差分故障分析,在31 轮利用故障模型“与”导入半字节故障,分别利用8 个和18 个故障恢复了TWINE 的80 bit 和128 bit 主密钥。2017 年,高杨等[20]利用S 盒的差分分布特性进行差分故障分析,采用随机半字节模型,在33 轮、34 轮、35 轮平均注入9 个故障,即可恢复TWINE 的80 bit 主密钥。此外,Nozaki 等[16]使用统计故障分析,通过在时钟中插入毛刺产生故障,统计40 对正确密文和错误密文对应的中间状态的汉明权重最小平均值,恢复了TWINE 的80 bit主密钥。现有的故障分析方法都是选择明文攻击的假设。
本文结合唯密文攻击的假设,对TWINE 密码进行了唯密文故障分析。此时攻击者仅依赖错误密文,攻击能力最弱,因此,唯密文故障分析的分析方案在现实的操作环境中具有更加灵活的应用前景。TWINE-80 和TWINE-128 的安全性分析对比如表1 所示。
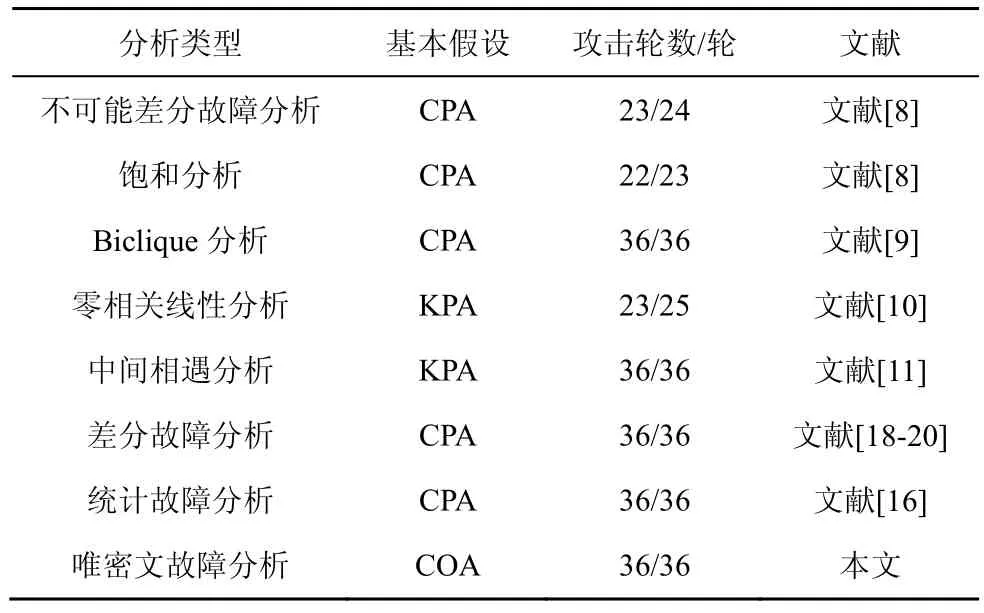
表1 TWINE-80 和TWINE-128 的安全性分析对比
在唯密文故障分析方面,2013 年,Fuhr 等[17]针对AES(advanced encryption standard)进行了唯密文故障分析,利用“与”故障模型,诱导随机字节故障生成错误密文,接着推导出对应的错误中间状态,利用平方欧氏距离(SEI,square Euclidean distance)、极大似然估计(MLE,maximum likelihood estimate)和汉明权重(HW,Hamming weight)等区分器筛选密钥候选值。实验结果表明,对于区分器SEI、MLE 和HW,分别导入320、224 和288 个随机字节故障就可以恢复AES 的子密钥。2016 年,Dobraunig 等[21]提出,攻击者可以在基于AES 的认证加密算法中注入故障进行破译。文献[22-24]采用唯密文故障分析的方法分别对轻量级密码算法LED(light encryption device)、SIMON 和MIBS等进行安全性分析,扩展了唯密文故障分析的范围。然而,对于具有广义Feistel 结构的TWINE能否抵御唯密文故障分析,国内外尚无文献发表。
本文给出了TWINE 的新型唯密文故障分析,提出了新型区分器极大似然估计-直方图估计(MLE-HE,maximum likelihood estimate-histogram estimate)、汉明权重-直方图估计(HW-HE,Hamming weight-histogram estimate)和汉明权重-极大似然估计-直方图估计(HW-MLE-HE,maximum likelihood estimate-hamming weighthistogram estimate)等区分器,不仅减少了故障数,而且提高了分析效率。唯密文故障分析破译AES、LED、SIMON、MIBS 和TWINE 子密钥的结果对比如表2 所示。
3 TWINE 密码介绍
3.1 术语说明
记X∈({0,1}4)16为明文,Y∈({0,1}4)16为正确密文,∈{0,1}4表示第i轮中输入的第j个半字节,其中,i∈[1,36]且j∈[0,15]。
记K为主密钥,k l为主密钥的第l个半字节,z表示主密钥半字节个数,∈{0,1}4表示第i轮子密钥的第t个半字节,为第i轮密钥编排时的轮常数,其中,H 表示高4 位,L表示低4 位,z∈{19,31},l∈[0,z],i∈[1,36]且t∈[0,7]。
记F为轮函数,S为混淆层,π为扩散层。
记~为导入故障后的错误值,<<<为循环左移,||为级联。
3.2 TWINE 描述
TWINE的分组长度为64 bit,主密钥长度为80 bit或 128 bit,分别表示为 TWINE-80 版本和TWINE-128 版本,迭代轮数为36 轮,TWINE 结构如图1 所示。加密部分和解密部分的结构相同,子密钥的使用顺序相反。算法1~算法3 分别给出了TWINE 的加密算法和不同版本的密钥编排方案。
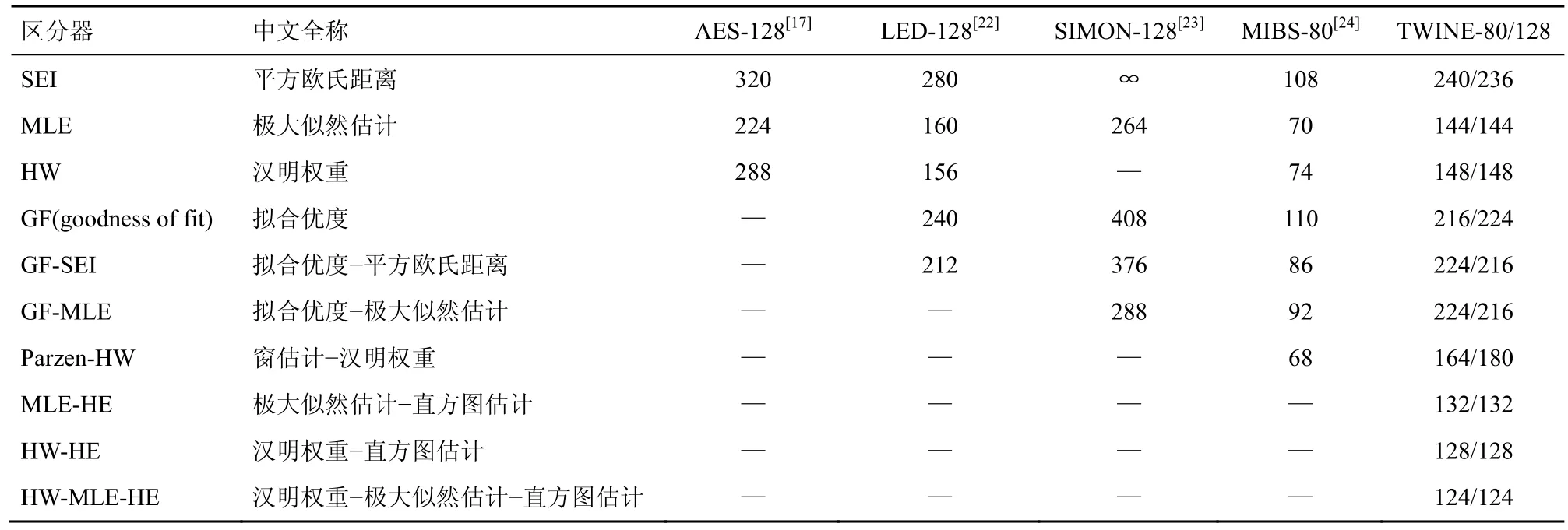
表2 唯密文故障分析破译AES、LED、SIMON、MIBS 和TWINE 子密钥的结果对比
算法1TWINE 的加密算法


4 唯密文故障分析
4.1 基本假设和故障模型
唯密文故障分析的基本假设是唯密文攻击,此时,攻击者可以使用相同主密钥对随机明文进行加密,运行过程中导入随机故障获取相应的错误密文;再利用故障导入前后对应的中间状态分布的偏离,从而破译密码。根据TWINE 的数据单元,本文采用了随机半字节的“与”故障模型,即
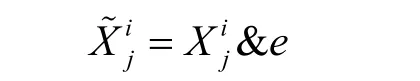
其中,表示第i轮的第j个半字节中间状态值,i∈[1,36]且j∈[0,15],表示对应的错误中间状态值,e表示随机半字节故障且e∈[0,15],&表示按位“与”操作。半字节被影响后的分布规律如图2所示。在具体实现时,软件通过结合中间状态与随机半字节故障,进行“与”代码操作实现,硬件通过外部时钟信号注入毛刺实现[25]。
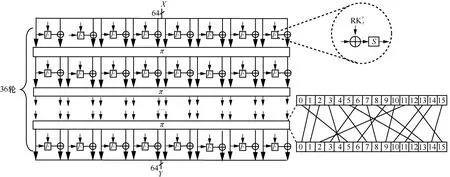
图1 TWINE 结构
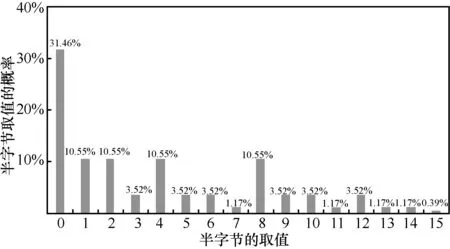
图2 半字节被影响后的分布规律
4.2 攻击步骤
针对TWINE 密码的唯密文故障分析包括以下3 个步骤。
步骤1故障注入。攻击者使用相同主密钥对随机明文进行加密,在加密运行过程中注入指定轮的随机半字节故障,并获取相应的错误密文。图3给出了半字节故障注入第33 轮随机位置时的故障扩散路径,以故障位置在首个半字节为例。
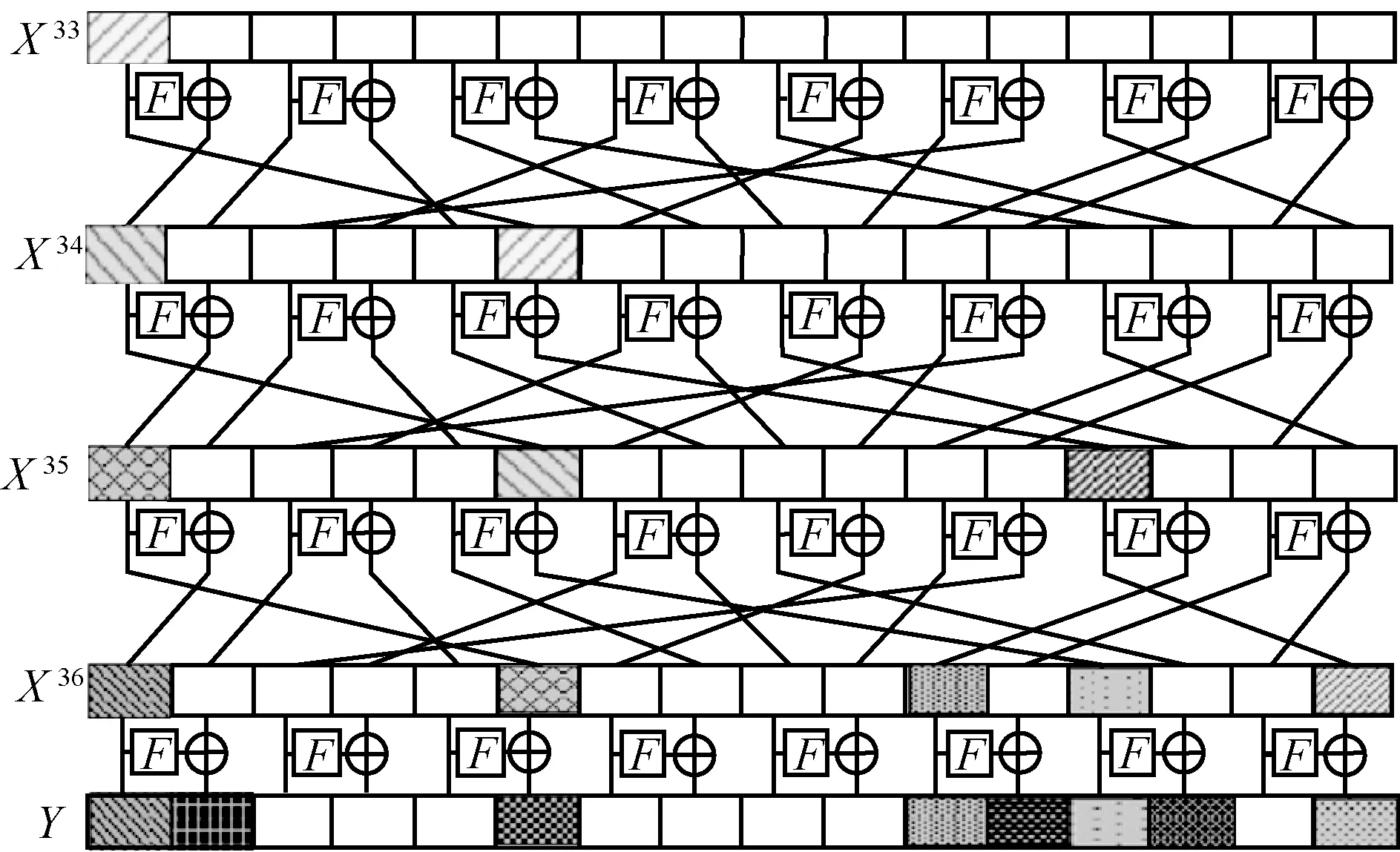
图3 半字节故障注入第33 轮随机位置时的故障扩散路径


步骤3破译主密钥。利用RK36解密最后一轮,获得第35 轮的输出,将故障注入第32 轮,同理可恢复出倒数第二轮子密钥RK35。依次类推,破译TWINE-80 版本主密钥K,最少需要3 轮子密钥RK36、RK35和RK34,过程如下。
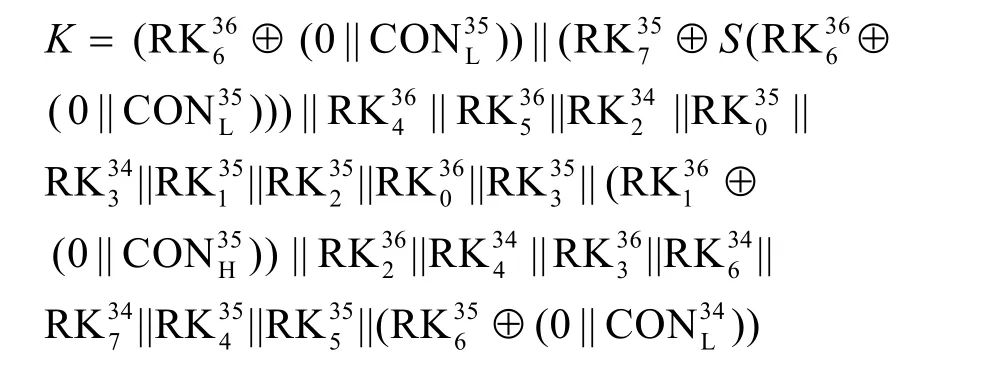
破译TWINE-128 版本主密钥K,最少需要5 轮子密钥RK36、RK35、RK34、RK33和RK32,过程如下。

4.3 区分器
4.3.1 已有区分器
1) SEI
SEI 由Fuhr 等[17]提出,用于计算实际分布与均匀分布之间的距离。在错误中间状态呈现不均匀分布时,若密钥候选值对应的错误中间状态的SEI值越大,则错误中间状态的实际分布与均匀分布距离越大。此时,SEI 最大值对应于正确的子密钥。SEI 表示为
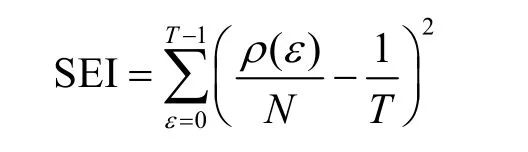
其中,T表示半字节所有可能取值的个数,N表示与密钥候选值相对应的一组错误中间状态个数,ρ(ε)表示错误中间状态值为ε的个数,T=24且ε∈[0,15]。
2) MLE
MLE 由Fuhr 等[17]提出,适用于已知错误中间状态的理论分布率的情况,如图2 所示。将每个错误中间状态的理论分布率相乘,计算与密钥候选值对应的错误中间状态发生的概率。此时,MLE 值越大,表示错误中间状态实际分布满足理论分布的可能性越大,即MLE 最大值对应于正确的子密钥。MLE 表示为
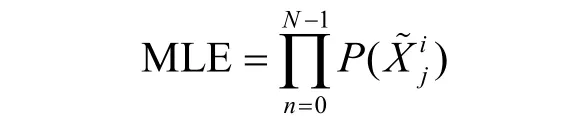
其中,P()表示错误中间状态值的理论概率,N表示与密钥候选值相对应的错误中间状态个数。
3) HW
HW 由Fuhr 等[17]提出,用于计算错误中间状态与相同长度的零字符串之间的汉明距离,其值等于错误中间状态的非零个数。密钥候选值对应的错误中间状态的HW 值越小,表示错误中间状态的零个数越多。此时,HW 最小值对应于正确的子密钥。HW 表示为
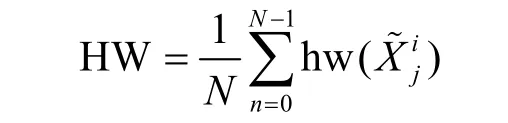
4) GF GF 用于测量实际分布与理论分布之间的拟合度[22]。密钥候选值对应的错误中间状态的GF 值越小,表示错误中间状态实际分布与理论分布之间的差异越小,即拟合度越大。此时,GF 的最小值对应于正确的子密钥。GF 表示为
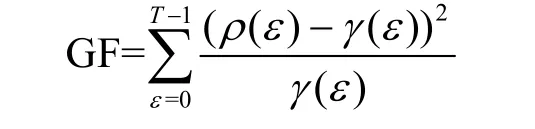
其中,T表示半字节所有可能取值的个数,ρ(ε)表示错误中间状态值为ε的个数,γ(ε)表示理论上错误中间状态值为ε的个数,T=24且ε∈[0,15]。
5) GF-SEI
GF-SEI 结合了GF 和SEI[22]。首先,攻击者使用GF 过滤掉不符合理论分布的密钥候选值,满足
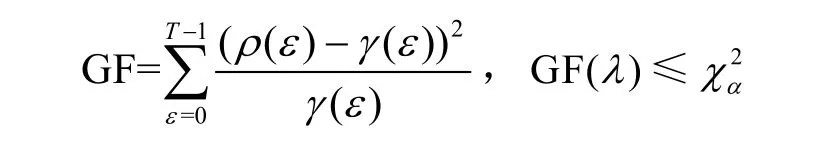
其中,表示从χ2分布上侧分位数表中查找的具有确定精度α的GF 临界值,λ表示筛选后的密钥候选值。然后,攻击者使用SEI 过滤保留的密钥候选值λ,满足

对于GF-SEI,正确的子密钥所对应的错误中间状态具有最小的GF 值和最大的SEI 值。
6) GF-MLE
GF-MLE 是由GF 和MLE 组合的双重区分器[23]。攻击者首先利用GF 区分器筛选出与密钥候选值对应的错误中间状态,保留符合理论分布的错误中间状态,满足
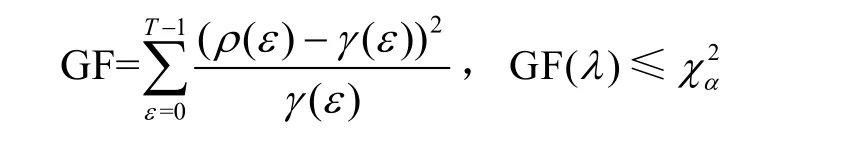
然后,攻击者使用MLE 选择使似然函数最大化的错误中间状态所对应的密钥候选值,满足

对于GF-MLE,正确的子密钥所对应的错误中间状态具有最小的GF 值和最大的MLE 值。
7) Parzen-HW
Parzen-HW 结合了Parzen 和HW 的优点[24]。首先,使用Parzen 进行无参估计,缩小密钥候选值的搜索空间。Parzen 的值越大,表示区域内样本数越多即对应可能的密钥候选值。Parzen 满足
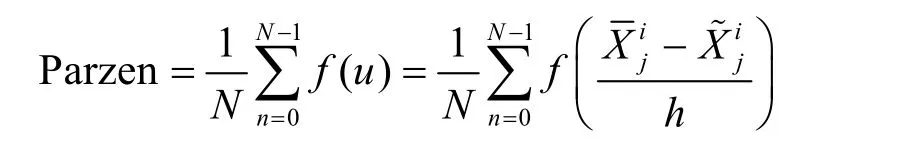
其中,f(u)是窗函数,表示以为中心,窗宽为h的区域内样本数量,N表示与密钥候选值对应的错误中间状态个数。然后,攻击者使用HW 对可能的密钥候选值进行筛选,满足
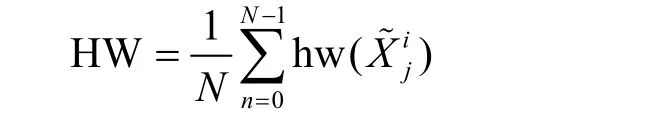
对于Parzen-HW,正确的子密钥所对应的错误中间状态具有最大的Parzen 值和最小的HW 值。
4.3.2 新型区分器
1) MLE-HE
直方图估计(HE,histogram estimate)以直方图法作为基础来计算密钥候选值的概率密度。由图2 可知,值较小的半字节出现概率较高,因此错误中间状态值的理论个数累加和占比越大,表示其出现较小半字节的次数越多,即对应正确的子密钥,HE 表达式为
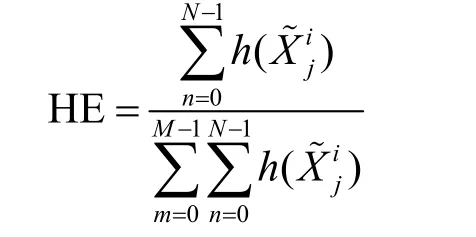
其中,N表示与密钥候选值相对应的错误中间状态个数,M表示所有密钥候选值的个数,h()表示错误中间状态的理论个数。
MLE-HE 结合了MLE 和HE 这2 种统计方法。首先,攻击者使用MLE 统计错误中间状态,筛选出部分可能的密钥候选值,满足

然后,攻击者使用HE 进一步筛选。对于MLE-HE,当错误中间状态同时具有最大的MLE值和HE 值,即该错误中间状态的分布满足理论分布且具有最大的概率密度时,则对应正确子密钥。
2) HW-HE
HW-HE 结合了HW 和HE 的优点,能够提高唯密文故障分析的效率。首先,攻击者使用HW 筛选出具有较小汉明距离的错误中间状态,满足

然后,攻击者使用HE 进一步筛选,概率密度最大的一组中间状态对应正确的子密钥,满足

对于HW-HE,基于按位“与”操作,半字节中出现0、1 的比例为3:1。当一组错误中间状态同时具有最小的HW 值和最大的HE 值时,则这组错误中间状态的0 和1 比例最大,因而最接近图2 的理论分布,那么该错误中间状态对应正确子密钥。
3) HW-MLE-HE
HW-MLE-HE 是在MLE-HE 和HW-HE 基础上的改进。首先,攻击者使用HW 缩小密钥候选值的搜索空间,满足
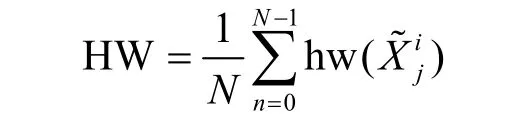
然后,攻击者利用MLE 进一步统计密钥候选值对应的错误中间状态,选择似然函数值较大的错误中间状态,满足

最后,攻击者使用HE 在剩余的密钥候选值中进行筛选、验证,确定唯一正确的子密钥。满足
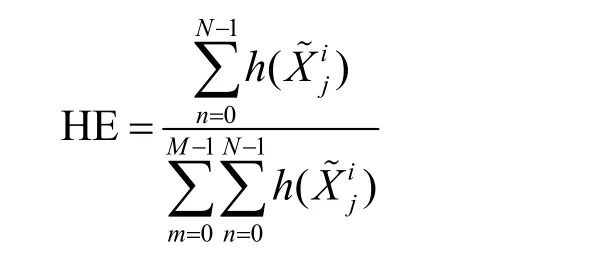
对于HW-MLE-HE,在筛选过程中,攻击者选择汉明权重较小的若干组错误中间状态,再比较各组错误中间状态的极大似然估计值,保留具有最大值的错误中间状态,其对应的密钥候选值中可能包含正确子密钥。为了保证所筛选的密钥的正确性和唯一性,利用HE 比较各组错误中间状态的概率密度,具有最大值的错误中间状态与图2 的理论分布最接近,即对应正确子密钥。所有区分器的对比如表3 所示。
5 实验分析
本实验采用Java 语言编程,利用计算机软件来模拟故障产生和注入,在密码算法运行过程中注入半字节故障。以TWINE-128 版本为例,唯密文故障分析每次恢复子密钥的16 bit,重复4 次,即可恢复最后一轮子密钥,依次类推,恢复最后5 轮子密钥,即可推导出128 bit 主密钥。在故障数、准确度、耗时和复杂度指标上,恢复TWINE 各版本的主密钥与恢复子密钥的16 bit 具有固定的比例关系。本节以恢复子密钥的16 bit 的实验数据为单元,计算衡量各区分器分析TWINE 各版本的效果。附录1 给出了所有实验数据。
5.1 故障数
故障数指破译密码主密钥或子密钥时,所需要注入的故障个数。在相同的成功率下,破译密码所需要的故障数越少,表明攻击代价越少。图4 给出了不同区分器恢复TWINE 子密钥的16 bit 的故障数与成功率之间的关系。其中,横坐标表示故障数,纵坐标表示成功率,不同曲线表示不同区分器唯密文故障分析的结果。以TWINE-128 版本为例,利用区分器SEI、MLE、HW、GF、GF-SEI、GF-MLE、Parzen-HW、MLE-HE、HW-HE 和HW-MLE-HE以至少99%的成功率恢复子密钥,最少需要注入的故障数为236、144、148、224、216、216、180、132、128 和124。与已有区分器相比,本文提出的 3 种新型区分器 MLE-HE、HW-HE 和HW-MLE-HE 需要的故障数较少,攻击效率高。此时,HW-MLE-HE 具有最少故障数。
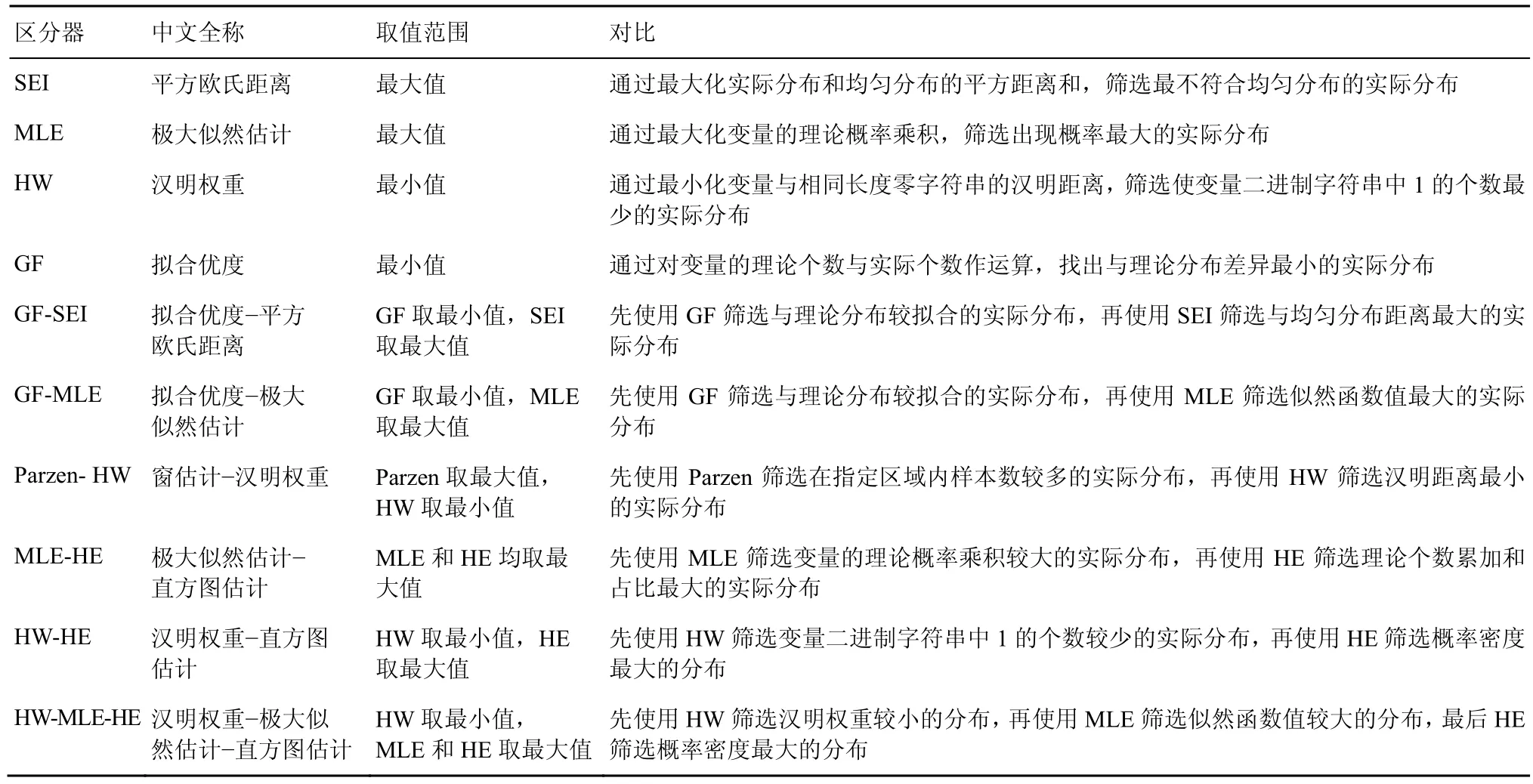
表3 区分器对比
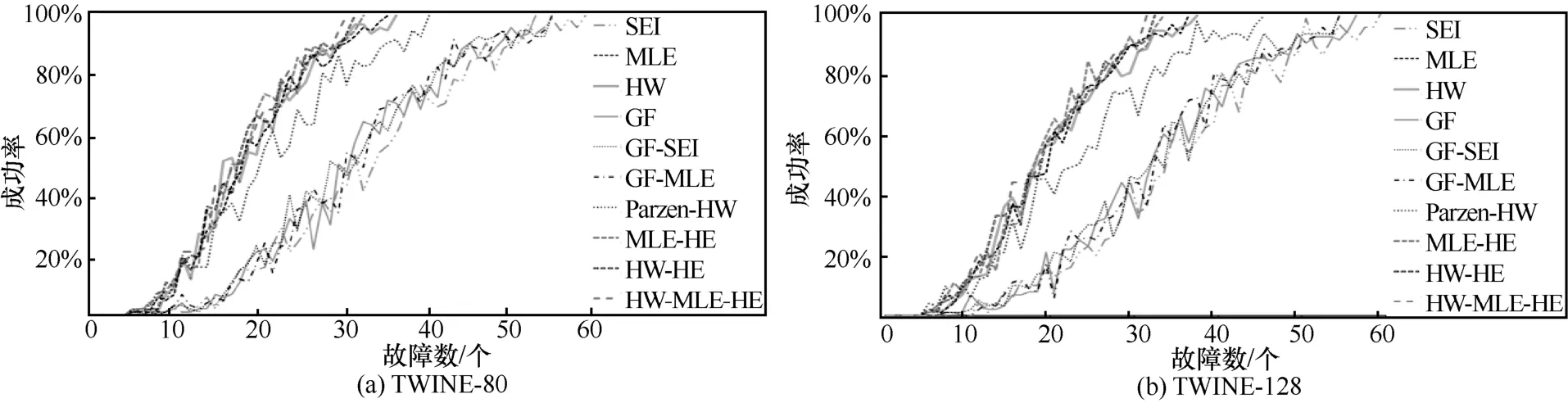
图4 不同区分器恢复TWINE 子密钥的16 bit 故障数与的成功率的关系
5.2 准确度
准确度用于衡量各区分器筛选出的密钥候选值个数与理论值个数之间的差距。本节使用平均绝对误差(MAE,mean absolute error)来衡量各个区分器的准确度。MAE 表示为
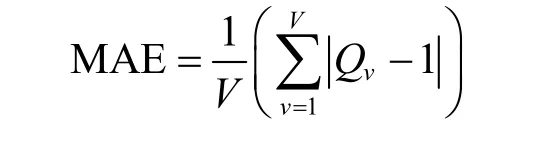
其中,V=1000表示实验次数,Q v表示第v次实验筛选出的候选值个数,第v次实验理论候选值个数为1。MAE 值越小,表示实验准确度越高。图5 给出了不同区分器恢复TWINE 子密钥的16 bit 的故障数与MAE 的关系。在相同故障数下,MLE-HE、HW-HE 和HW-MLE-HE 的MAE 值小于已有区分器的MAE 值,且快速逼近于0,此时,HW-MLE-HE具有最小MAE 值。
5.3 耗时
耗时是指恢复密钥所花费的时间,包括导入故障、遍历候选密钥和统计中间状态所消耗的时间。图6 给出了不同区分器恢复TWINE 子密钥的16 bit的故障数与耗时之间的关系,其中横坐标表示故障数,纵坐标表示耗时,不同的曲线表示不同区分器。以TWINE-128 版本为例,利用区分器SEI、MLE、HW、GF、GF-SEI、GF-MLE、Parzen-HW、MLE-HE、HW-HE 和HW-MLE-HE 恢复子密钥最少需要的时间分别为11.6 s、14 s、7.2 s、14 s、13.6 s、16.8 s、9.6 s、14.4 s、7.2 s 和8.4 s。此时,HW 和HW-HE 耗时最少,HW-MLE-HE 次之。
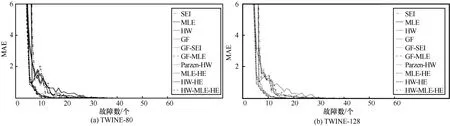
图5 各区分器恢复TWINE 子密钥的16 bit 的故障数与MAE 的关系

图6 各区分器恢复TWINE 子密钥的16 bit 的故障数与耗时的关系
5.4 复杂度
时间复杂度和数据复杂度用于衡量破译密码时所需要的时间量和数据量。表4 给出了不同区分器恢复TWINE 子密钥的时间复杂度和数据复杂度。新型区分器MLE-HE、HW-HE 和HW-MLE-HE的复杂度均小于现有区分器的复杂度,其中HW-MLE-HE 的复杂度最小。
本节采用故障数、准确度、耗时和复杂度等指标衡量各个区分器对TWINE 密码进行唯密文故障分析的效果。从图4~图6 和表4 可以看出,新型区分器MLE-HE、HW-HE 和HW-MLE-HE均有效减少了故障数,成功率达到99%及以上,其中,HW-MLE-HE 所需要的故障数较少、准确度较高、复杂度较小;HW-HE 和HW-MLE-HE耗时较少。一般情况下,故障数是衡量唯密文故障攻击的首要标准。因此,在资源受限的物联网环境下,建议采用HW-MLE-HE 对TWINE 密码进行唯密文故障分析,可以达到相对较好的攻击效果。
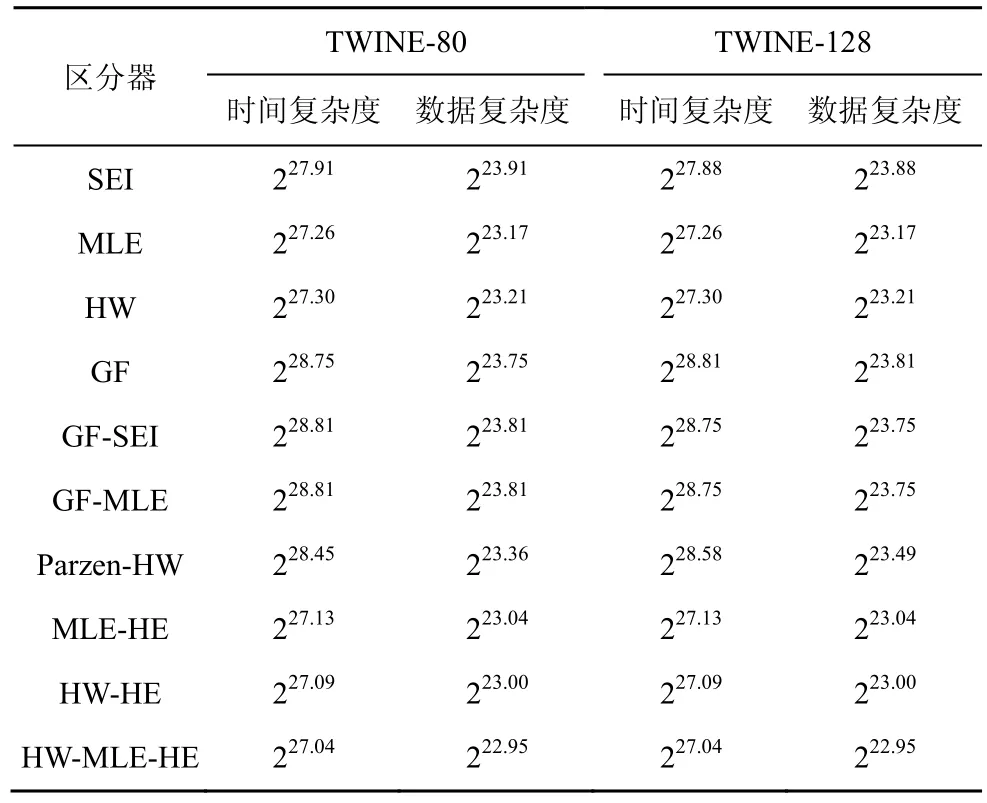
表4 不同区分器恢复TWINE 子密钥的复杂度
6 结束语
本文针对TWINE 密码抵抗唯密文故障分析的安全性进行了研究,提出的新型区分器MLE-HE、HW-HE 和HW-MLE-HE,均可以减少攻击所需的故障数,并提高攻击效率。研究表明,TWINE 密码易受到唯密文故障分析的威胁,在物联网中使用该密码时,设计人员需采取有效措施用于抵御唯密文故障分析的攻击。
附录1 实验数据
明文:随机生成
TWINE-80 版本主密钥:00112233445566778899
TWINE-128 版本主密钥:00112233445566778899AABBCCDDEEFF
本文中所有实验数据如表5~表7 所示。
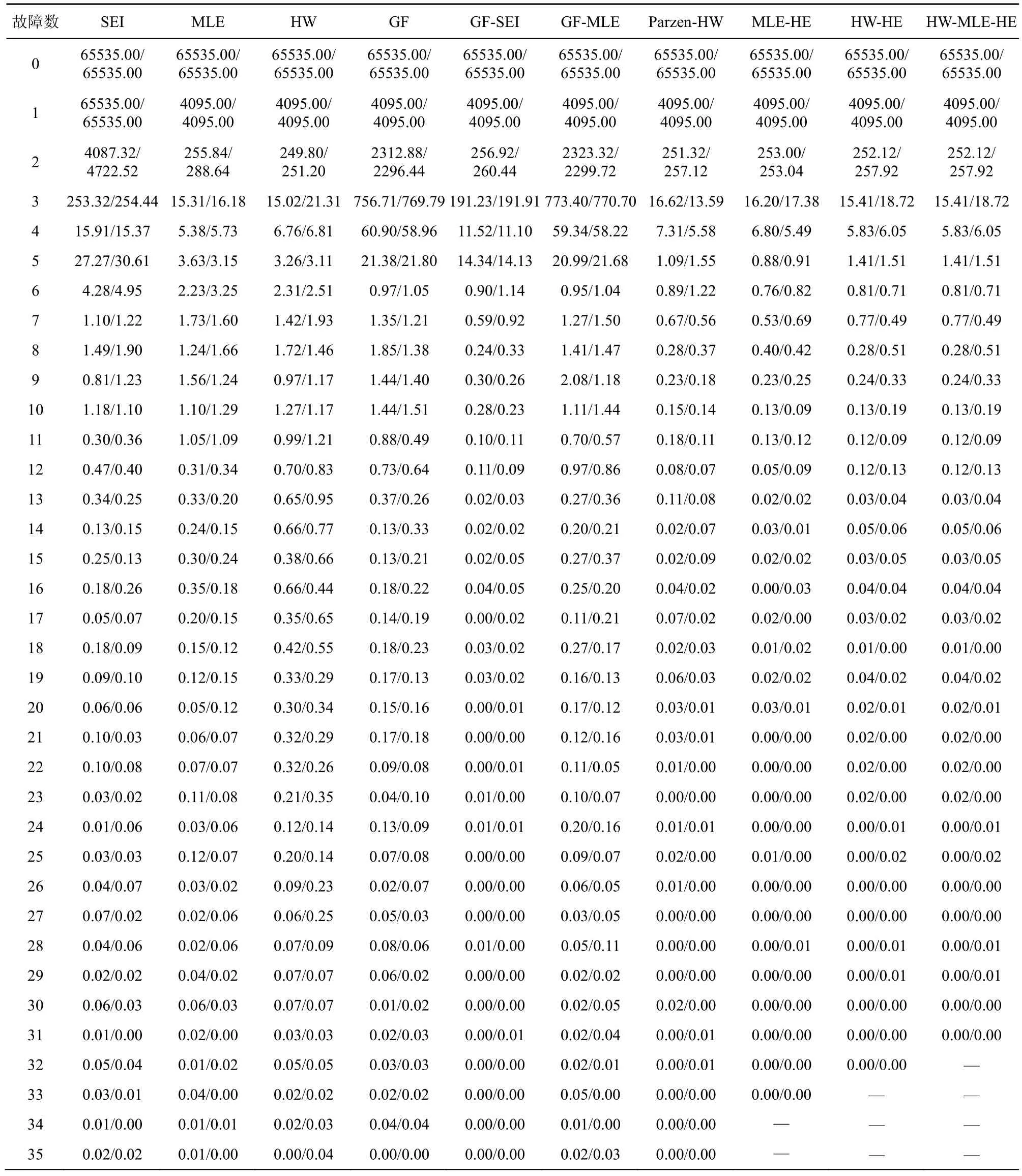
表5 各区分器恢复TWINE-80 和TWINE-128 子密钥的16 bit 的MAE 值
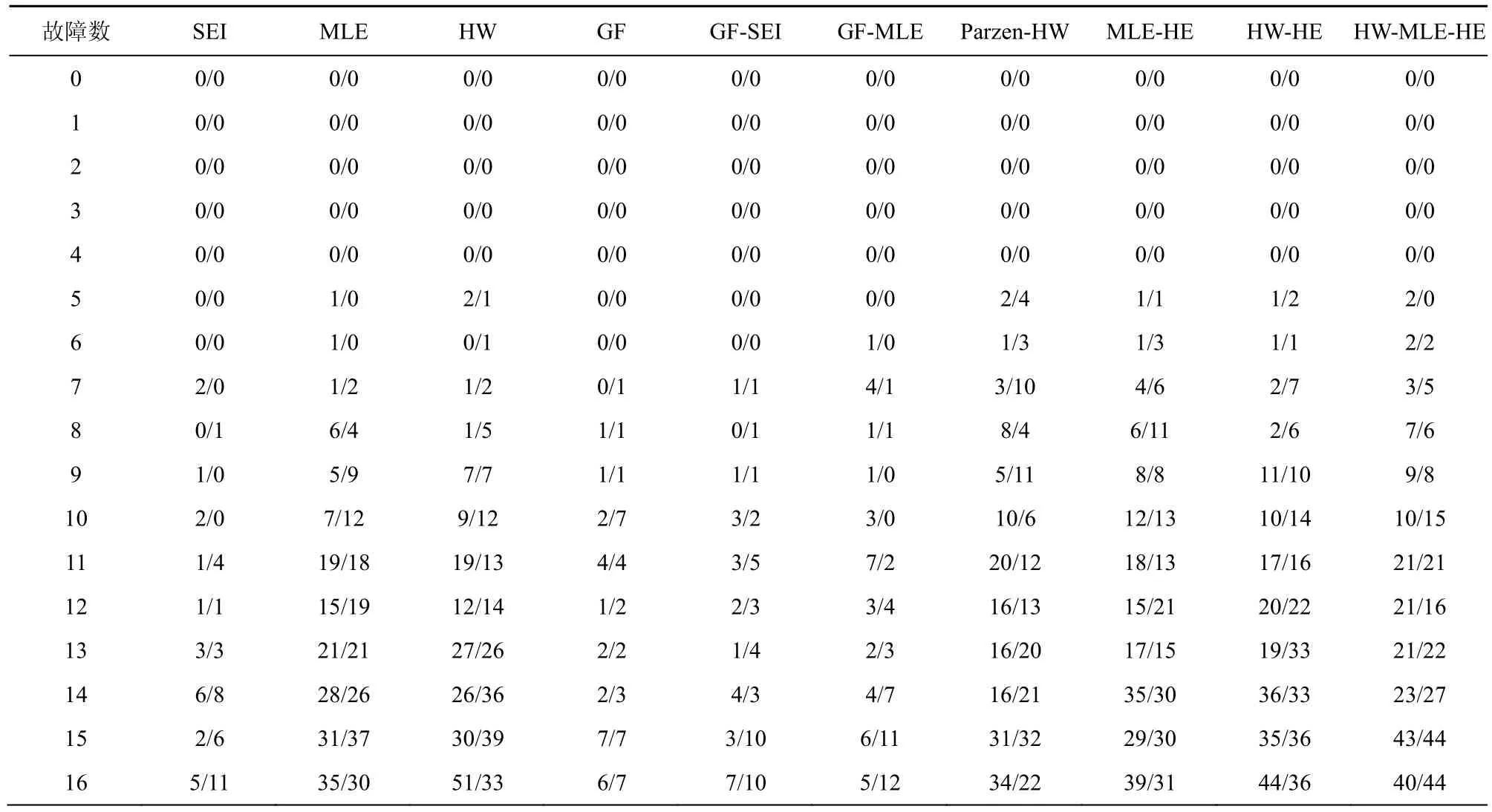
表6 各区分器恢复TWINE-80 和TWINE-128 子密钥的16 bit 的成功概率
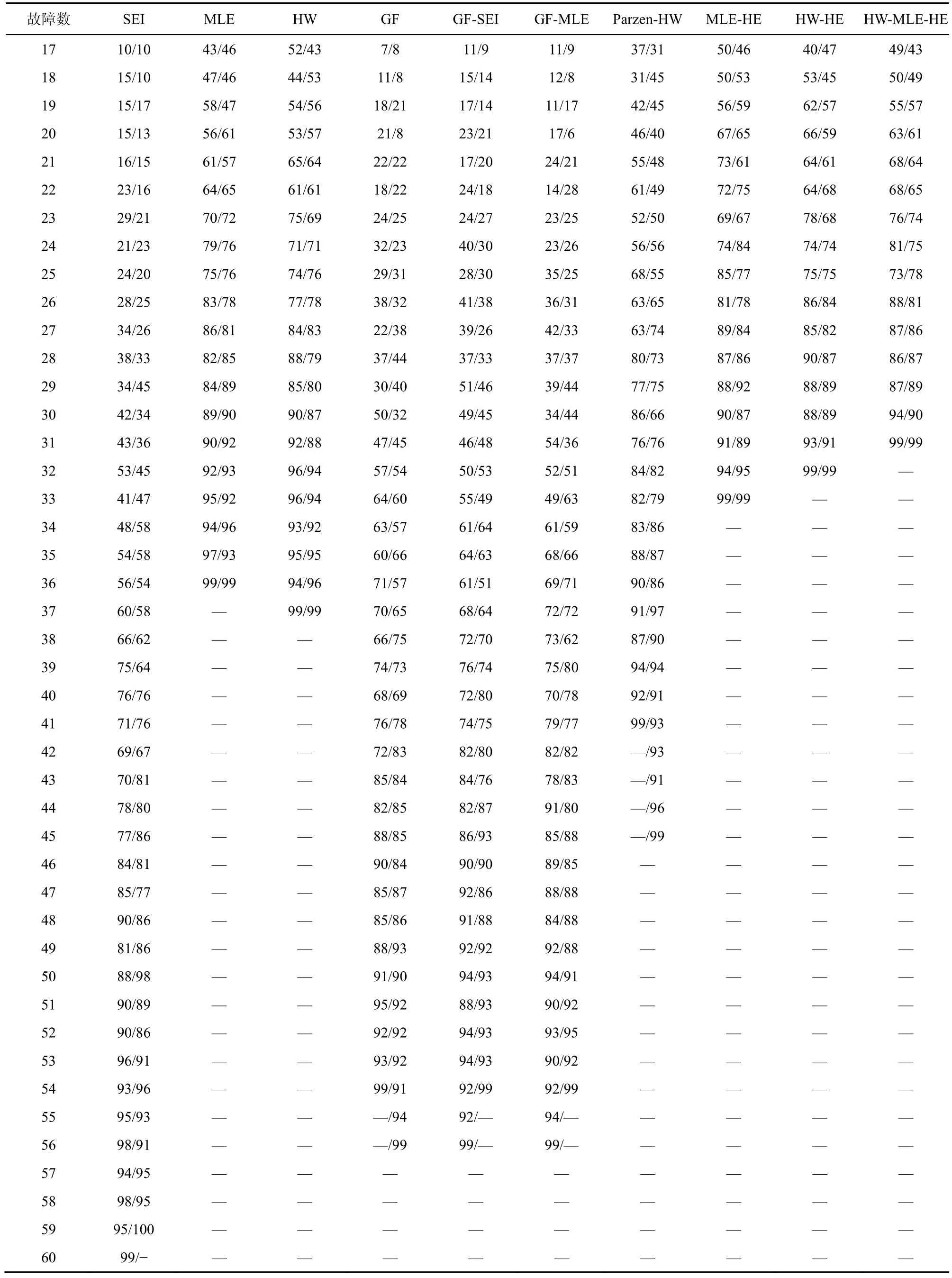
(续表6)

表7 各区分器恢复TWINE-80 和TWINE-128 子密钥的16 bit 的时间

(续表7)
