基于决策变量交互识别的多目标优化算法
2021-04-09王丽萍潘笑天
王丽萍,林 豪,潘笑天,俞 维
(1.浙江工业大学 计算机科学与技术学院,浙江 杭州 310023;2.浙江工业大学 信息智能与决策优化研究所,浙江 杭州 310023;3.浙江工业大学 管理学院,浙江 杭州 310023)
多目标优化问题(Multi-objective optimization problems, MOPs)指的是多个冲突目标需要同时优化的问题,这些问题广泛存在于实际应用中,例如环境与资源配置[1-2]、金融[3]、通信与网络优化[4-5]、云计算[6]及交通运输[7-8]等。这些问题不能通过直接的方式来求解,因此,利用多目标进化算法(Multi-objective evolutionary algorithms, MOEAs)求解MOP成为当下最热门的研究领域。但是,大多数现有的算法主要集中在目标函数的可扩展性上,随着决策变量规模的增加,大规模问题的搜索空间呈指数级增长,搜索空间的地形发生改变,其性能通常会迅速恶化[9]。因此,有效地解决大规模优化问题是进化优化领域中的研究热点与难点。目前,大规模优化算法已经被广泛应用于单目标优化的求解[10]。受大规模单目标优化算法研究的启发,大规模多目标优化中引入了一些在大规模单目标优化中被证明有效的方法,以提升算法的可扩展性[11-12]。一部分学者受协同进化(Cooperative coevolution,CC)[13]思想的启发,将具有高维变量的MOP分解为多个含有更低维度的子组件,然后利用现有的MOEA优化每个子组件。例如,Antonio等[14]提出基于随机固定分组的大规模多目标进化算法CCGDE3,将空间维度为D的决策变量通过随机分解机制将其分解为规模相同的K个子组件,并运用差分进化算法协同地对每个子组件进行优化。Huband等[15]进一步研究发现:决策变量存在控制属性,即修改某一个决策变量的值会改变新解的多样性或者收敛性。受此启发,Ma等[16]提出一种基于决策变量分析的MOEA,即MOEA/DVA,用于解决大规模多目标优化问题。在MOEA/DVA中,基于优势关系的决策变量分析方法将决策变量分为3 种:1)多样性相关变量;2)收敛相关变量;3)与收敛和多样性相关的混合变量。收敛相关变量进一步被分成许多低维子组件,对不同子组件中的变量逐一进行优化。Zhang等[17]遵循MOEA/DVA的关键思想,提出一种基于决策变量聚类的大规模多目标优化进化算法LMEA。Chen等[18]提出了一种基于协方差矩阵的可扩展小种群自适应进化策略,即S3-CMA-ES。该算法通过使用一系列的子群体来解决大规模多目标优化问题(Large-scale many-objective optimization problems, LSMOP)[19],并采用CMA-ES[20]来优化每一个子种群。由于分而治之的方法,CC的可扩展性赋予了它解决具有更高维度和更高计算负担的问题的巨大能力[21]。对于大规模决策变量问题,结合变量分组策略和协同进化(CC)思想的算法有助于更好的优化LSMOP性能。求解LSMOP的关键在于决策变量分解,但是准确检测决策变量间的关联性通常需要大量的适应度评价,当决策变量规模逐渐增大时,优化算法在分组过程中适应度评价大量消耗,导致用于进化过程的适应度评价的数量减少,导致解集的收敛性下降。
基于此,笔者提出一种基于决策变量交互识别的多目标优化算法,即MOEA/D-IRG算法。该算法提出一种决策变量交互识别分组策略,将大规模多目标优化问题的决策变量分解为一组含有简单的低维变量的子组件,有效地降低决策变量分组过程中适应度评价的消耗,同时确保每个子组件间的相关性最低,以提高算法的收敛性;并在决策空间中根据个体间的角度来划分子组件的邻域范围,提升所求解集的多样性,进一步提高解集的整体质量。
1 背景知识
1.1 大规模多目标优化问题
多目标优化问题(MOP)涉及多个同时优化的冲突目标[19],可以表述为
minF(x)=(f1(x),f2(x),…,fM(x))
s.t.x∈X
(1)
式中:X∈Rm为决策空间;x=(x1,x2,…,xn)为决策向量;M,n分别为目标函数和决策变量的数量。此外,一个MOP具有至少100 个决策变量,即n≥100,它被称为大规模多目标优化问题(LSMOP)。
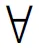
1.2 函数可分离性
大规模优化通常是指针对具有数百甚至数千决策变量的优化问题寻找解决方案[22]。而随着决策变量数量的增加,搜索空间的体积也随之呈指数型扩张,其适应度地形也越发复杂。其中,更大的困难在于变量的不可分性,也就是决策变量间的相关性。
定义1对于一个可分离函数f(x),当且仅当决策变量xi(i=1,2,…,n)能被独立优化时,则满足的条件[23]为
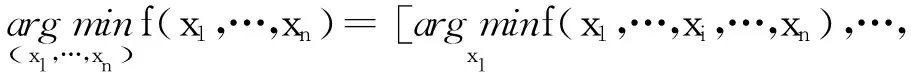
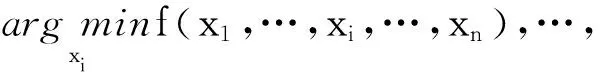
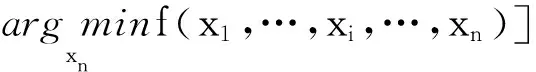
(2)
若不满足条件式(2),则函数f(x)为不可分离函数,即变量xk对适应度值的影响仅取决于其自身,独立于任何其他变量。此外,决策变量xk与一个或多个其他决策变量进行交互,则f(x)是不可分离函数。决策变量间交互是问题的一个重要方面,它们描述了问题的结构。定义1表明一个可分离函数f(x)的决策变量xk是可以独立优化。可分离性函数意味着问题中涉及的决策变量可以独立于任何其他变量进行优化,而不可分离函数意味着在至少两个决策变量之间存在交互。两个决策变量xi和xj之间交互的定理[24]如下。
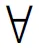
Δδ,xp[f](x)|xp=a,xq=b1≠Δδ,xp[f](x)|xp=a,xq=b2
(3)
其中
Δδ,xp[f](x)=f(…,xp+δ,…)-f(…,xp,…)
(4)
定理1表示如果式(3)用任意两个不同x求值,求得不同的结果,说明两个决策变量xp和xq存在交互关系。
2 MOEA/D-IRG算法
2.1 算法框架
将决策变量交互识别分组策略结合基于分解的多目标进化算法MOEA/D[25]中,形成MOEA/D-IRG算法的主要框架,其具体步骤为
步骤1设置参数,并初始化种群。
步骤2变量交互分析,根据算法2对决策变量进行分组。
步骤3邻域选择,为个体分配不同的邻域。
步骤4利用MOEA/D优化每一个子组件。
步骤5判断是否达到最大适应度评价次数,若是,则输出当前种群,否则转步骤4。
该算法主要包括两个方面:决策变量分组过程和子组件优化过程。在变量分组过程中,通过决策变量交互识别策略算法可将决策变量分为许多不相关的子组。在子组件优化过程中,首先根据决策空间中个体间的角度大小来确定个体的邻域范围,然后每个子组件结合MOEA/D单独进化。MOEA/D-IRG算法伪代码如下。
算法1MOEA/D-IRG算法伪代码
输入:种群规模N,决策变量维数D,最大函数评价次数FEmax
输出:最终种群
1)Initialize the population pop←{x1,…,xD}
2)Subcomponents←grouping(pop, obj,m,n) //use Algorithm 2
3)Neighbour←Neighbour(pop) //
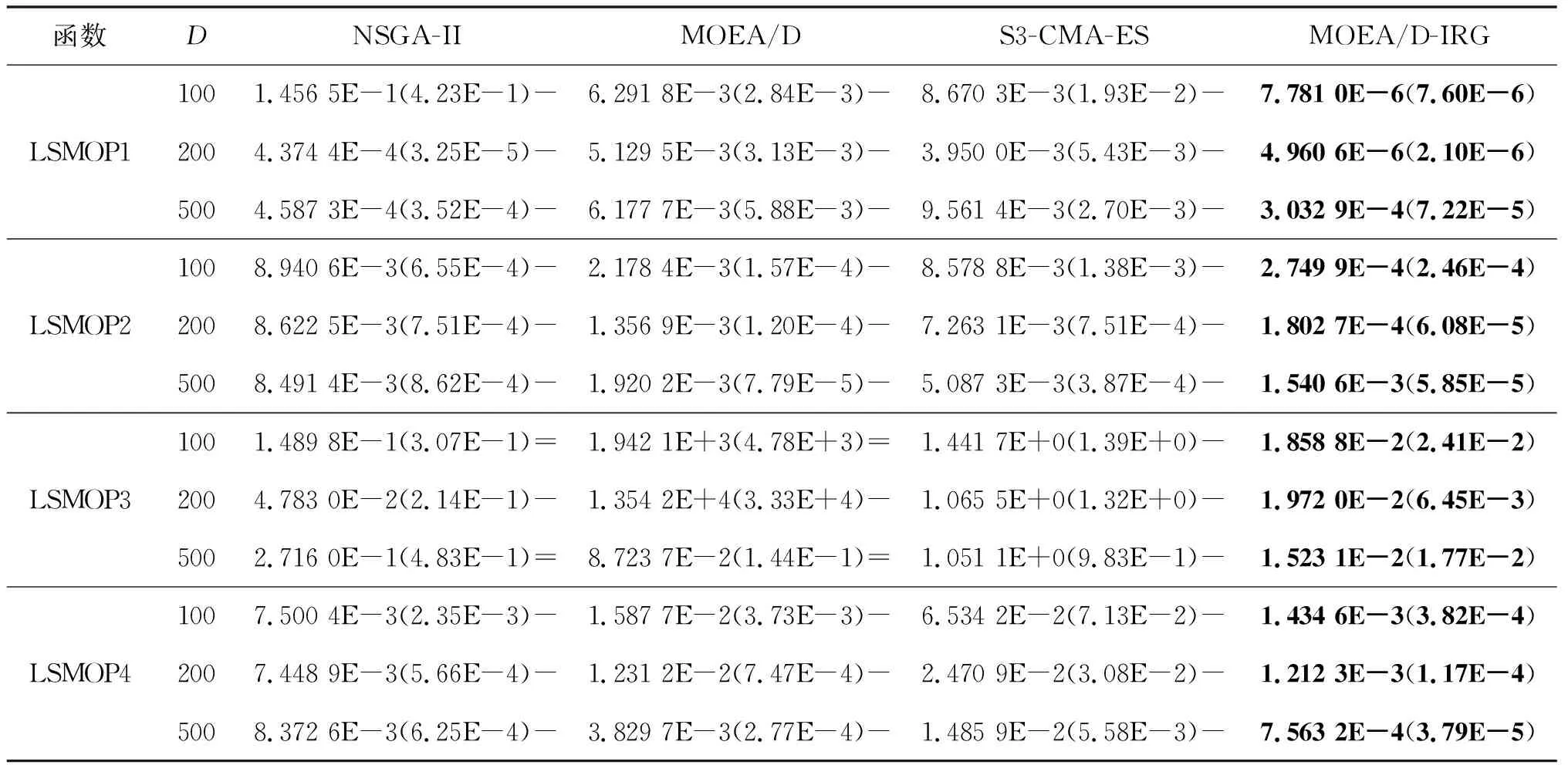
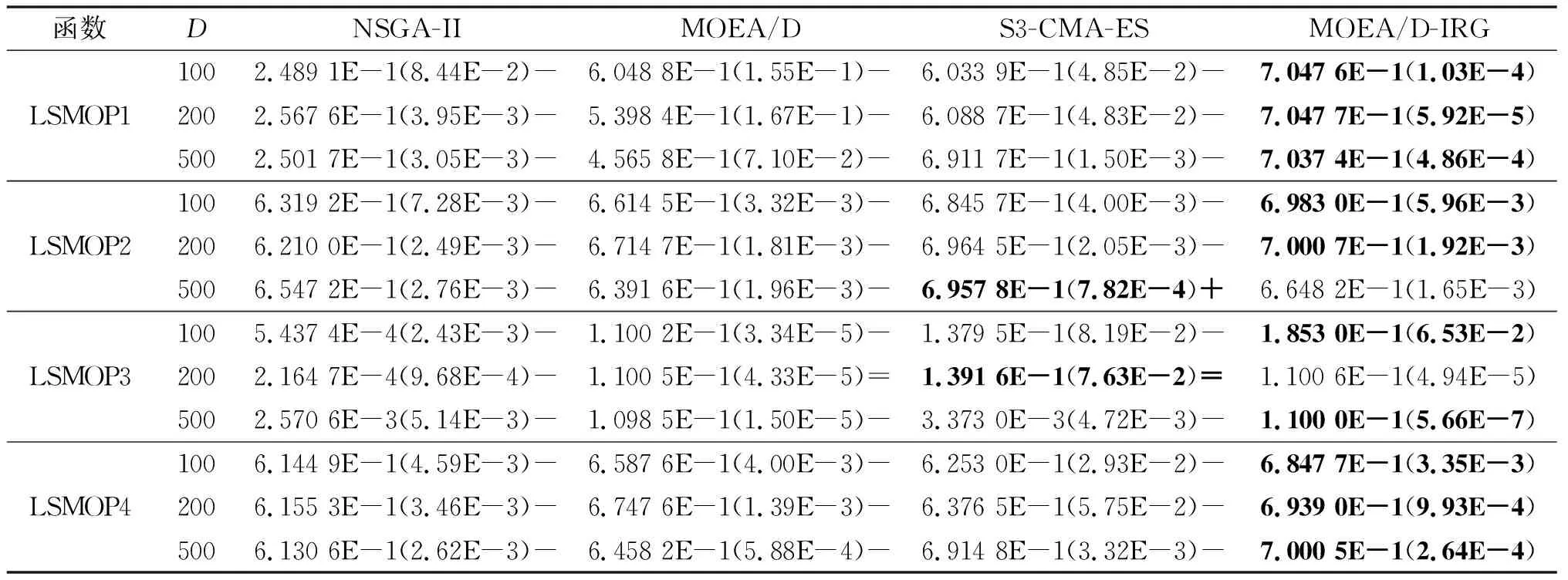
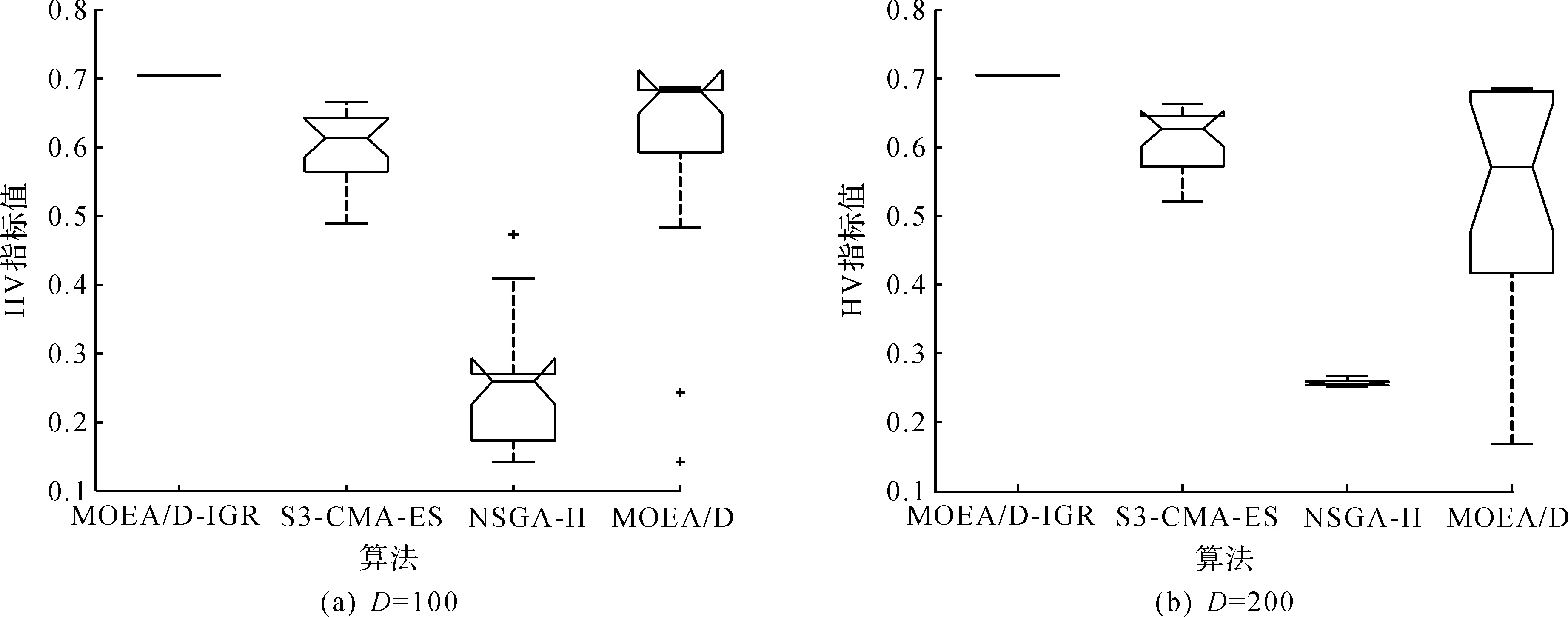
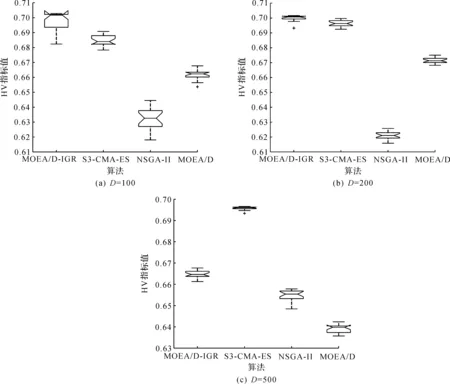
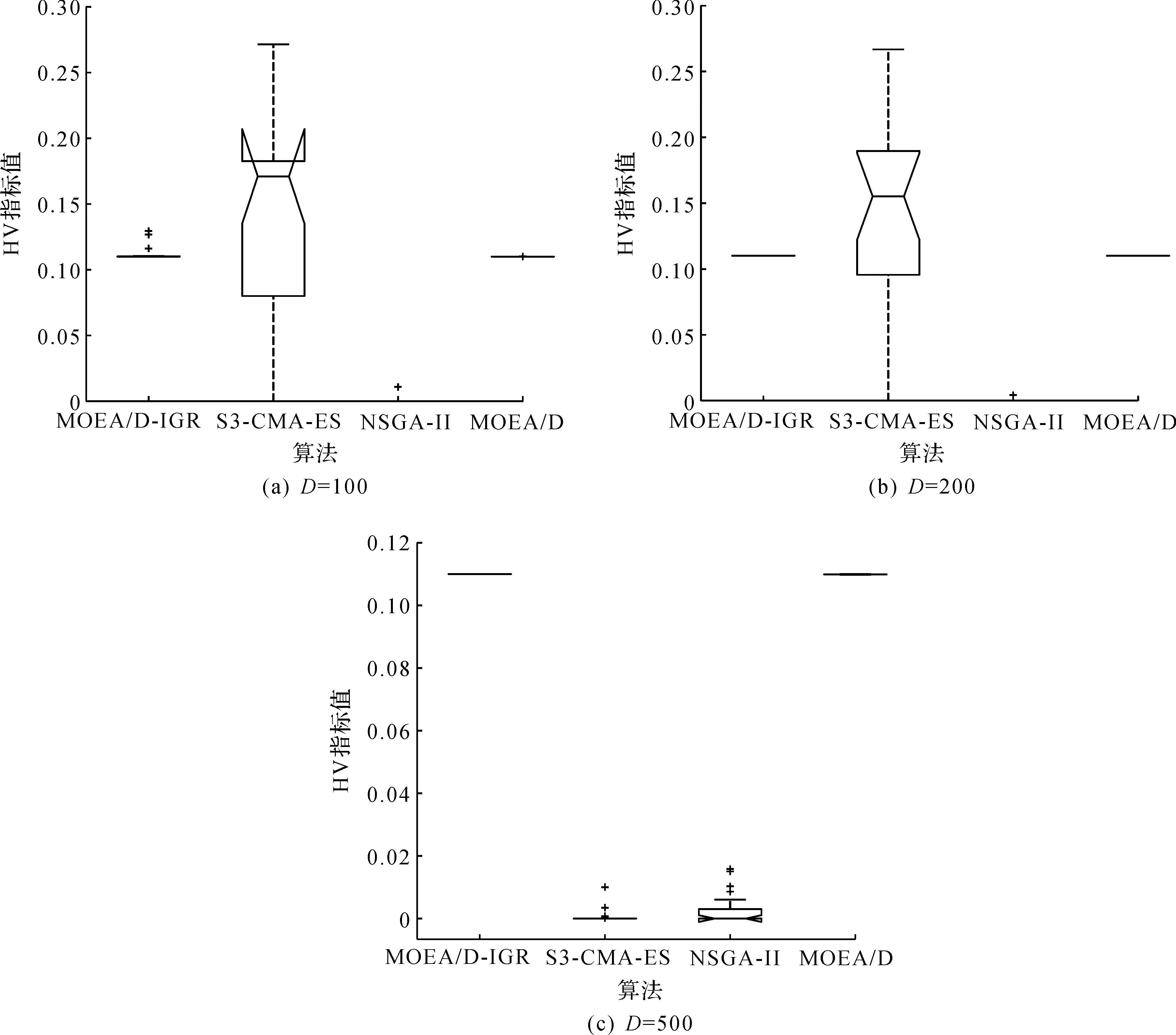
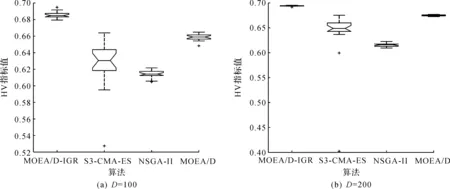
4)WhileFE 5)Fori=1 to size(Subcomponents) 6)pop=Optimizer(Population,Neighbour,Subcomponents{i}) //use MOEA/D to evolve 7)FE=FE+N 8)End For 9)End While 在MOP中,决策变量间交互存在于许多目标中,这极大地增加了准确分组维度的难度。然而,准确检测变量间的相关性通常需要大量的适应度评价。笔者提出决策变量交互识别分组策略,可以显著减少适应度评价次数,该策略如下。 算法2决策变量交互识别策略 输入:种群规模N,当前进化种群P←{x1,…,xD}及其目标函数值F←{F1,…,FN},决策变量维数D 输出:每个子组变量索引 1)Randomly select an individualx1fromP←{x1,…,xD}, EvaluateF(xl) 2)Fori=1 toD-1 3)Forj=i+1 toD 5)Fork=1 tom 6)EvaluateΔ1use Equation(2) //For the sake of brevity the left hand side of(1)is denoted byΔ1 7)EvaluateΔ2use Equation(2) //For the sake of brevity the right hand side of(1)is denoted byΔ2 8)IFΔ(k)=Δ1*Δ2<0, Then detect interaction betweenxiandxjforfk(x) 9)End For 10)End For 11)End For 为了实现算法2对决策变量精确分组,必须对所有决策变量进行交互检查。根据定理1可知:任意决策变量xi和xj相互作用都遵循的计算式为 d1=F(…,x′i,…)-F(x1,…,xn) (5) d2=F(…,x′i,…,x′j,…)-F(…,x′j,…) (6) 根据定理1计算D维决策变量所需适应度总数为2D(D-1),但这种模型导致适应度计算冗余,冗余计算数量为 (7) 因此,适应度评价次数应为总数减去冗余的适应度评价次数,这就得到最后的适应度评价总数为D(D+1)/2+1。 为了降低随机因素对算法性能的影响,在每个测试函数上独立运行20 次,取其平均值和标准差作为最终测试值。为了验证MOEA/D-IRG算法的性能,仿真实验将MOEA/D-IRG算法与典型算法S3-CMA-ES[18]、MOEA/D[25]和NSGA-II[26]在PlatEMO[27]平台进行比较分析,3 种对比算法的实验参数按照各自参考文献设置。 选取的测试函数为大规模多目标基准测试问题LMSOP1~4[19]。在仿真实验中,设定种群规模为100,扩展LSMOP1~4测试问题的决策变量规模分别为100,200,500。当且仅当最大函数评价次数分别达到1 200 000,2 500 000,6 800 000时结束算法。各对比算法均独立运行20 次。 图1~4为LSMOP1~4测试函数在决策变量规模分别为100,200,500的情况下由MOEA/D、NSGA-II、S3-CMA-ES以及MOEA/D-IRG算法得到的Pareto前沿对比图。由图1~4可知:MOEA/D-IRG算法在不同决策变量规模下,均能较好地收敛到真实的Pareto前沿。MOEA/D-IRG算法在多样性和收敛性方面求得的解集质量最好,其次是S3-CMA-ES和MOEA/D,而NSGA-II解集质量最差。而对于图3,在LSMOP3上,MOEA/D-IRG算法虽然没有收敛到真实的Pareto前沿,但是显示出较好的分布,而3 种对比算法MOEA/D、NSGA-II和S3-CMA-ES却完全无法收敛到前沿。这是由于测试函数LSMOP3属于复杂多模态测试函数,具有最困难的适应度地形,并且在目标空间中初始种群位置远离真实的Pareto前沿。随着决策变量数量的增加,对比算法S3-CMA-ES的Pareto前沿明显恶化,MOEA/D、NSGA-II的Pareto前沿恶化最显著,甚至无法收敛到前沿,MOEA/D-IRG算法仍然能获得高质量的解集。原因在于MOEA/D-IRG算法通过变量交互识别策略将决策变量分解成一组含有更低维度的子组件,降低了MOP的优化难度,加速种群收敛,并在决策空间为每个子组件划分不同的邻域范围,提高解集的均匀性。 图1 LSMOP1测试函数在不同决策变量规模下的Pareto前沿对比图 图2 LSMOP2测试函数在不同决策变量规模下的Pareto前沿对比图 图3 LSMOP3测试函数在不同决策变量规模下的Pareto前沿对比图 为了评价算法的收敛性及多样性,采用超体积指标(Hyper volume,HV)[28]、世代距离指标(Generational distance, GD)[29]和空间分布指标(Spacing,SP)[30]评价算法的性能。HV指标用于衡量算法收敛性与多样性的指标,HV值越大,算法求得解集质量越高;GD指标用于衡量算法收敛性的指标,GD值越小,说明算法所求解集的收敛性越好;SP指标用于衡量算法多样性的指标,SP值越小,说明算法所求解集的多样性越好。同时用T-test检验MOEA/D-IRG算法性能的显著性,其中“+”“-”“=”分别表示所测指标值在5%的显著水平下,该算法的性能优于、劣于和无差别与对比算法。 3.3.1 收敛性分析 表1是LSMOP1~4测试函数决策变量规模扩展到100,200,500的规模时,4 种算法独立运行20 次获得的GD指标的均值和方差。由表1数据可知:对于LSMOP1和LSMOP2测试函数,当决策变量规模为100和200时,MOEA/D-IRG均优于其他3 种对比算法;当决策变量规模为500时,MOEA/D-IRG劣于S3-CMA-ES,但严格优于MOEA/D、NSGA-II。对于LSMOP3测试函数,当决策变量规模为500时,MOEA/D-IRG均优于其他3 种对比算法;当决策变量规模为100和200时,性能略差。对于LSMOP4测试函数,随着决策变量规模的增加,MOEA/D-IRG算法求得解集的GD指标值仍然保持最小,且明显优于其他对比算法。对比结果表明:MOEA/D-IRG算法在测试函数LSMOP1~4所获得解集质量整体优于S3-CMA-ES、MOEA/D和NSGA-II等所求解集质量,更加接近真实的Pareto前沿。说明变量交互识别策略能有效地识别决策变量间的潜在关系,将决策变量分解成一组具有更低维度的子组件,从而降低了测试问题的优化难度,以便于种群快速收敛于真实的Pareto前沿。 表1 4 种算法在LSMOP1~4上的GD指标结果 3.3.2 多样性分析 表2是4 种算法在LSMOP1~4测试函数决策变量规模扩展到100,200,500的规模下运行20 次的SP指标结果。分析数据可知:MOEA/D-IRG算法在LSMOP1~4测试函数上所求解集的SP指标值最小,说明该算法所求的解集具有较好的多样性,其次是S3-CMA-ES和MOEA/D,而NSGA-II最差。随着决策变量规模的增加,MOEA/D-IRG算法所获得解集的SP指标均优于S3-CMA-ES、MOEA/D和NSGA-II,说明该算法所求得的解集分布性更好。对比表2数据结果发现:MOEA/D-IRG算法能够提高所求解集的整体质量,较好地维护解集的多样性。原因在于通过决策变量交互识别策略进行变量分组优化,同时为每个子组件在决策空间划分不同的邻域范围,可以有效地解决大规模多目标优化问题。 表2 4 种算法在LSMOP1~4上的SP指标结果 3.3.3 综合评价性能评价 表3列出了4 种算法计算LSMOP1~4测试函数在100,200,500决策变量规模上独立运行20 次所求得的HV均值和标准差。 表3 4 种算法在LSMOP1~4上的HV指标结果 分析数据可知:MOEA/D-IRG算法在LSMOP1和LSMOP4测试函数上求得最大的HV指标值,这说明MOEA/D-IRG算法所求得解集更加地接近真实的Pareto前沿,具有更好的收敛性与分布性,性能明显优于3 种对比算法。在LSMOP2测试函数决策变量规模为500时,MOEA/D-IRG算法劣于S3-CMA-ES,但明显优于MOEA/D、NSGA-II。对于LSMOP3测试函数,MOEA/D-IRG算法严格优于NSGA-II,但在决策变量规模为200的情况下,MOEA/D-IRG算法无差别于MOEA/D算法,劣于S3-CMA-ES算法。原因在于LSMOP3测试函数是复杂多模态函数,且是不可分离函数与最难分离函数的线性组合,算法收敛到Pareto前沿所需适应度评价次数较大。同时随着决策变量数量的增加,MOEA/D-IRG算法求得解集的HV指标值仍然保持最好,且明显优于S3-CMA-ES、MOEA/D和NSGA-II所求解集质量。说明MOEA/D-IRG算法在解决大规模多目标优化问题上能够得到更高质量的解集,能够更好地平衡收敛性与多样性之间的冲突,从而改善算法整体性能。 为了更加直观地体现算法的稳定性,图5~8给出了4 种算法在决策变量规模为100,200,500的情况下,在LSMOP1~4测试函数上独立运行20 次的HV指标值的盒图。图5是LSMOP1测试函数在不同决策变量规模下,4 种算法运行20 次的HV指标盒图的对比情况。从图5可以发现:MOEA/D-IRG算法所求解集的HV指标值中位数更高,说明算法所求的解集质量较高,综合性能优于3 种对比算法,同时四分位距离最小,即盒子长度最短,说明算法鲁棒性较好。 图5 不同决策变量规模下LSMOP1测试函数的HV盒图 图6 不同决策变量规模下LSMOP2测试函数的HV盒图 图7 不同决策变量规模下LSMOP3测试函数的HV盒图 图8 不同决策变量规模下LSMOP4测试函数的HV盒图 对于图6,7,LSMOP2测试函数在决策变量规模为500以及LSMOP3测试函数在决策变量规模为200时,MOEA/D-IRG算法性能劣于S3-CMA-ES,弱优于MOEA/D和NSGA-II。但MOEA/D-IRG不容易出现异常值,即使出现异常值也明显少于3 种对比算法,说明MOEA/D-IRG算法的鲁棒性较好。 图8表明:MOEA/D-IRG算法在求解LSMOP4测试函数时,可以获得较高质量的解集,对应的中位数更高,四分位距离最小,说明算法的精度和鲁棒性较好。并且MOEA/D-IRG算法所求得解集的HV指标最小值大于或等于3 种对比算法的HV指标的最大值,随着决策变量规模的增加,MOEA/D-IRG算法获得的解集质量更高,鲁棒性更好。 从上述算法性能指标对比结果可以看出:MOEA/D-IRG算法在求解大规模多目标优化问题上,可以获得高质量的解集,求解精度以及算法性能指标整体上均优于S3-CMA-ES、MOEA/D和NSGA-II,随着决策变量规模的增加,优势更加明显。主要原因在于:1)MOEA/D-IRG与MOEA/D、NSGA-II和S3-CMA-ES相比具有更快的收敛能力,该算法通过将决策变量分解成一组具有更低维度的子组件,降低了MOP的优化难度,同时每一个子组件都是各自独立优化,以加速种群的收敛;2)MOEA/D-IRG在分组之后,在决策空间为每个子组件划分不同的邻域范围,以优化目标空间中种群的均匀性。 针对大规模多目标优化问题,随着决策变量规模的增加,准确检测变量间的相互关系所消耗的适应度评价次数增加,导致算法在优化过程中所需适应度评价次数减少,使得算法的收敛性下降。提出了基于决策变量交互识别的大规模多目标优化算法(MOEA/D-IRG算法),通过决策变量交互识别策略识别决策变量之间存在的潜在结构,将决策变量分解成一组具有更低维度的子组件,通过决策变量交互识别策略,降低了分组过程中适应度评价次数的消耗,同时确保了每个子组件间的相关性保持最低,以提升算法的收敛效率,并在决策空间中根据每个体间的角度关系为每个子组件划分不同的邻域范围,来进行优化求解,以提升所求解集的多样性,提高所求解集的整体质量。通过对大规模多目标专用测试函数LSMOP1~4的决策变量规模扩展后进行仿真实验,实验结果表明:MOEA/D-IRG算法在求解精度和性能指标上完全优于多目标算法MOEA/D、NSGA-II和S3-CMA-ES;但当目标函数是复杂多模态函数且为不可分离函数时,MOEA/D-IRG算法难以收敛到Pareto前沿,因此该算法在处理多模态函数和不可分分离函数上仍有待进一步研究。2.2 决策变量分析与分组
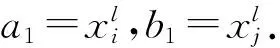
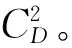
2.3 邻域选择
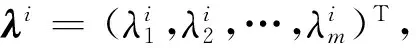
3 实验及结果分析
3.1 参数设置
3.2 Pareto前沿对比分析
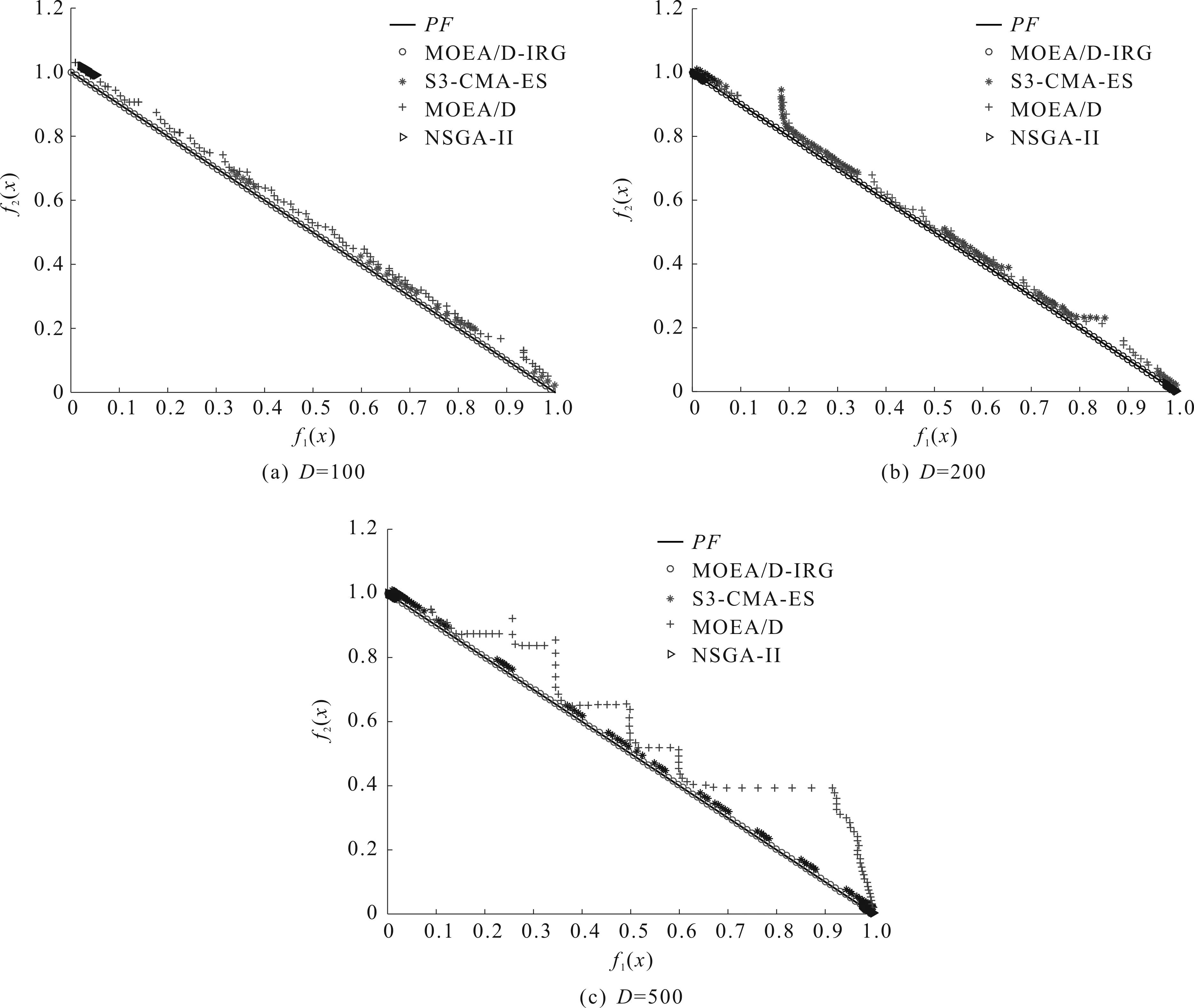
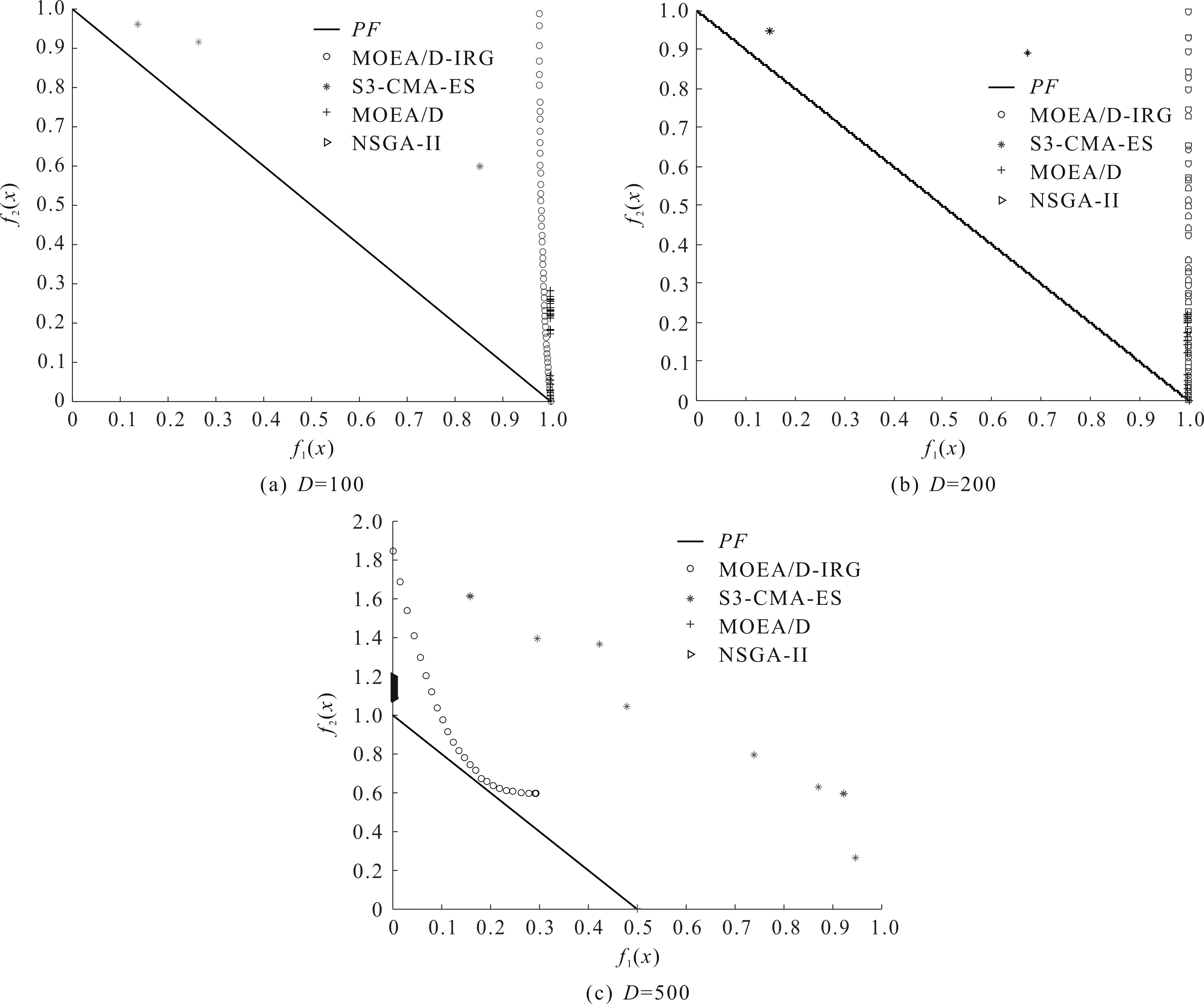
3.3 算法性能分析
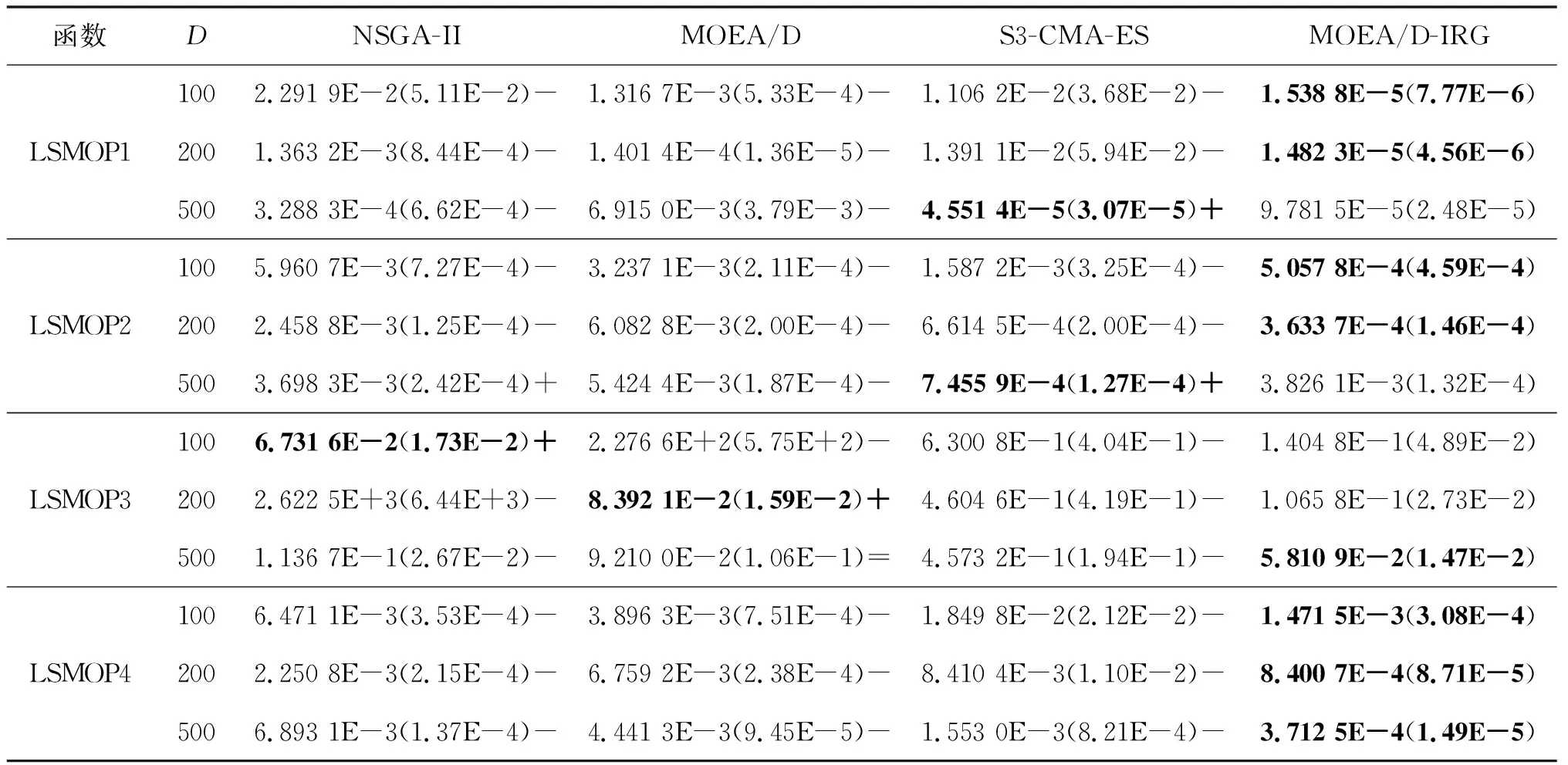
4 结 论
