电动叉车叉子转角检测系统设计

王 磊，李天剑

(北京信息科技大学 机电工程学院，北京 100192)

0 引言

电商的飞速发展，引领智能仓储物流行业进入新的纪元，仓储物流机器人受到越来越多的关注和重视[1]，在拣选、码垛以及搬运等诸多环节得到了广泛的运用。无人驾驶电动叉车能够帮助企业降低人工成本，提升工作效率，促进企业智能转型，有助于实现智能化仓储生产管理新模式[2-3]。无人驾驶电动叉车工作时，叉子的动作是一个不稳定的非线性系统[4]。因为是无人驾驶系统，需要传感器替代视觉对货架及叉车叉子的倾斜角度进行感知[5]；由于叉子本身颤动加上货物影响，导致叉子的角度检测困难[6]。本文提出一种使用陀螺仪和加速度计通过卡尔曼滤波融合计算角度的方法，对电动叉车叉子进行状态估计。实验结果表明，此方法可以快速准确地返回叉子倾角。

1 系统结构组成

无人驾驶电动叉车叉子的转角检测系统主要包括上位机运算模块、下位机的控制模块与检测反馈模块。上位机模块主要由倍福控制器、PC端和显示器组成：PC端编写倍福程序，通过以太网将程序发送至倍福控制器，通过显示器观察程序运行情况。下位机的控制模块主要由控制系统、液压系统和电源管理系统组成，控制系统又由松下PLC、数字步进电机驱动器和JULI电机构成：松下PLC接收倍福控制器的指令，对数字步进电机驱动器发送指令，控制电机驱动，进而控制液压系统，从而控制叉车叉子的运动；电源管理系统为各个模块提供电能。检测反馈模块主要由加速度计、陀螺仪构成[7-8]，将获取的数据发送到PC端，进而分析数据。无人驾驶电动叉车叉子的转角检测系统结构如图1所示。

图1 电动叉车叉子转角检测系统结构

转角检测模块MPU6050[9]用来读取叉车叉子的姿态，包括加速度计和陀螺仪。加速度计用来检测叉子运动的加速度，陀螺仪检测叉子转动的角速度。系统采用数字式MPU6050模块，其内部自带稳压电路可兼容3.3 V/5 V供电电压，可以通过USB转TTL电平的串口模块，将MPU6050连接至上位机PC端。MPU6050模块接线图如图2所示。

图2 MPU6050模块接线图

2 软件设计

叉车在获取货物的同时，需要反馈系统不断调整叉子的转角，从而获取叉子的最佳倾角，获取货物。同时，叉子的运动轨迹是一个实时非线性的系统，需要不断对叉车叉子的转角进行检测。系统采用MPU6050获取电动叉车叉子的初始加速度和角速度，通过卡尔曼滤波融合得到精准的倾角信息。叉车叉子检测流程如图3所示。

图3 叉车叉子检测流程

求电动叉车叉子倾斜角度时，通过MPU6050读取叉车叉子在x、y方向的加速度，进一步求解叉子倾角。叉子的力学分析如图4所示。

图4 叉子的力学分析

从图中可以看出，角度a、c同与角度b互为余角，那么有：

(1)

式中：gx为x方向叉车叉子发生倾角的加速度；g为y方向叉车叉子的加速度。要计算叉车叉子的倾角，只需要求a的角度。由于反正弦函数求解a困难，且叉车叉子倾角范围为[-π/6,π/6]，因此，可以用相近的一次函数替代正弦函数，进而求得叉车叉子倾角。相近的一次函数如图5所示。

图5 不同角度相对于不同函数的曲线

从图5可以看出，横坐标x轴坐标范围为 [0,π/2]。从上到下，第一条、第二条、第三条曲线的函数表达式分别为：

y=πx/180

(2)

y=0.95πx/180

(3)

y=sinx

(4)

图5中,区间[0,π/6]的曲线可以满足要求，选择式(3)替代正弦曲线，就可以得到角度a：

(5)

3 卡尔曼滤波的实现

在叉子动态测量过程中，叉子倾角和角速度与其真实情况相比，存在一定的偏差。本文采用卡尔曼滤波算法将加速度计与陀螺仪采集的数据融合，克服陀螺仪造成的漂移误差和加速度计造成的动态误差，得出最优值消除误差，有效优化叉子姿态数据信息，提高输出精度。

除招收本科生以外，台湾的大部分应用型大学还招收硕士生，有的还招收博士生，人才培养层次较高，招收的硕士生也基本为应用型硕士，具有较为完备的应用型人才培养体系。以德明财经科技大学为例，该校除招收本科生以外，还在资讯管理、财政税务、金融服务管理等领域招收硕士生。

卡尔曼滤波的主要作用是利用信号、噪声的状态空间模型，以最小方差为最优估计准则，依据前一次的状态预测出当前检测值，然后与实测状态比较，来修正估计出当前状态。卡尔曼滤波的使用，可以有效防止和基本消除噪点，有效地将数据融合，来纠正实测数据，使结果更准确、更高效。卡尔曼滤波系统流程如图6所示。

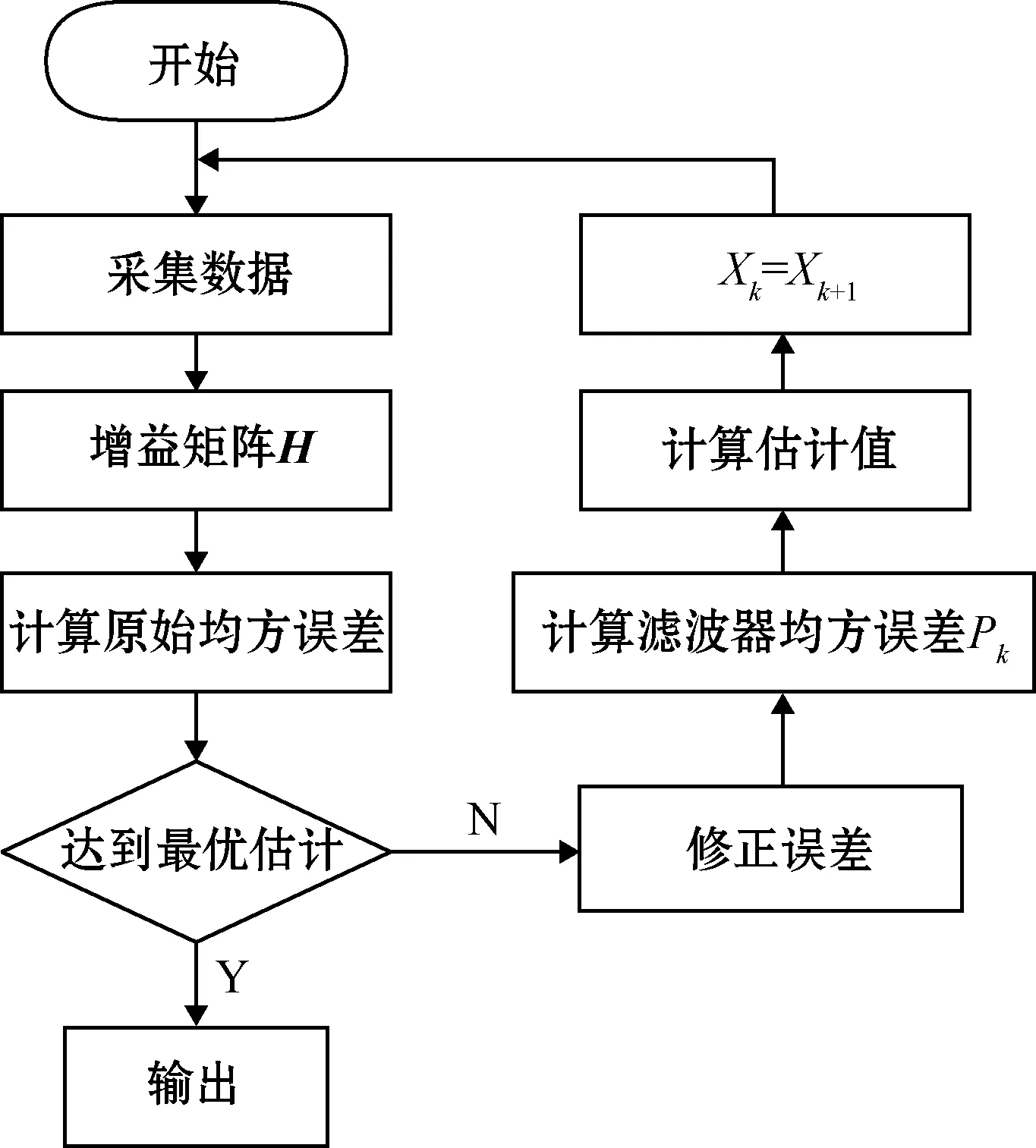
图6 卡尔曼滤波系统流程

首先利用卡尔曼滤波系统的过程模型，来预测下一状态。假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态：

Xk=Xk-1+Buk

(6)

式中：Xk为现在的状态预测；Xk-1为上次的状态预测；B为将输入转为状态的矩阵；uk为此时状态的控制量，如果没有控制量，它可以为0。系统更新后，对应于Xk-1的协方差还需要更新。用P表示协方差，有：

Pk=APk-1AT+Q

(7)

式中：Pk为Xk对应的协方差；Pk-1为Xk-1对应的协方差；A为状态转移矩阵；Q为系统过程的协方差。式(6)、式(7)是对系统的状态预测。

在状态预测结果的基础上，收集现在状态的测量值；结合预测值和测量值，得到现在状态k的最优化估算值X：

X=Xk+K(yk-HXk)

(8)

式中：H为状态变量到测量的转换矩阵；K为卡尔曼增益：

K=PkHT/(HPkHT+R)

(9)

其中R为测量噪声协方差。为了卡尔曼滤波器不断运行下去直到系统过程结束，需要更新k状态下X的协方差：

P=(I-KH)Pk

(10)

其中I为1的矩阵，对于单模型单测量，I=1。当系统进入k+1状态时，P就是式(7)的Pk-1。也就是说卡尔曼滤波是时间更新和状态更新两个步骤不断迭代的过程。此外，考虑陀螺仪受外界的干扰比较大，因此在计算中需要减去零点漂移，这样可以减少误差。

4 实验结果与分析

卡尔曼滤波调试是将传感器的返回值，通过卡尔曼滤波算法进行数据融合，读取处理后的角度数据，不断调整参数，使其输出稳定有效的波形。对倾角数据融合时，需要通过单片机将波形信号发送到电脑上，通过上位机获取融合后的信号。不断调整参数，直到波形满足融合的精度要求。当叉车取货时，叉子受到很大的外力，运动角度突变很大，会产生相应的波形。波形整定后可以大大减少叉子运动角度突变，原始波形和整定后的波形如图7所示。

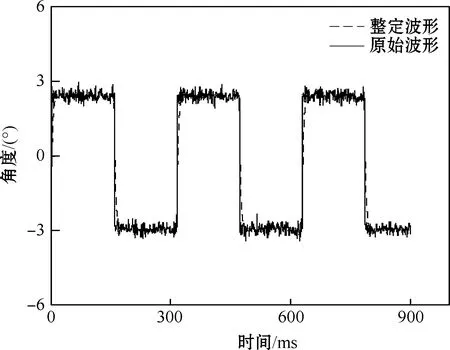
图7 叉子运动角度突变时，原始波形和整定后的波形

在静止状态下，轻触叉车叉子，叉子受到力的作用后，其波形也会发生相应的变化，原始波形和整定后的波形如图8所示。

图8 叉子静止时，轻触叉子，原始波形和整定后的波形

从图中可以看出，在叉子运动时由于运动角度的突变，产生较为震荡的波形；经过整定之后，滤波更加平稳，大大减少了角度突变，基本满足融合的精度要求。

5 结束语

本文设计了一种无人驾驶电动叉车叉子的转角检测系统。基于改进卡尔曼滤波算法，对通过加速度求解的角度和y轴的角速度进行融合处理。利用位移测量值与状态预测值进行加权计算得到状态估计值，以状态估计值参与后续迭代，在数次迭代后能够消除初始参数的误差，读取处理后的角度数据，不断调整参数。通过叉车叉子的故障真实值与叉车叉子的运动姿态的对比表明，本文方法可以实现传感器故障良好地重构，明显提升了叉车叉子的转角检测稳定性，有较大的实用价值。